2. 地质灾害防控协同创新中心, 四川 成都 610059
2. Collaborative Innovation Center of Geohazard Prevention, Chengdu 610059, P. R. China
岩石力学是地质工程、采矿工程、水利工程、交通土建工程等专业,以及土木工程专业岩土和地下建筑课群组本科生必修的专业基础课程之一,主要研究解决工程岩体在各种力场作用下变形破坏规律以及强度和稳定性问题,在工程实践中有着广泛的应用[1],其中地下工程是岩石力学的一个重要应用方向,如公路和铁路隧道、地下厂房等。
建造地下工程时会遇到各种岩石力学问题,如岩体的二次应力分布、围岩压力的计算、开挖后围岩的稳定性评价等问题。如何有效地理解掌握这些理论知识,是岩石地下工程教学环节中极为关键的部分[2]。
然而传统的教学方法存在以下不足之处。
(1) 传统教学方法以书本为依托,主要采用理论公式推导,最终采用公式形式及少量图表进行展示,教学形式枯燥,不能给学生留下直观形象的印象。
(2) 传统教学方法中,对于复杂的岩石地下工程问题,理论公式参数较多,很难分辨每个参数对结果的具体影响程度。
(3) 传统教学方法中,受书本篇幅及侧重点限制,较少加入实际工程和数值模拟的数据及结果,不利于理论与实际应用的结合。
数字教学平台是计算机虚拟仿真技术的一种应用方式,它是指以计算机为依托,采用仿真模拟技术模拟真实事件,同时可以对理论公式进行参数分析并进行直观展示的平台,目前已经被广泛应用到军事、工业、教育等行业[3-4]。数字教学平台作为一种辅助教学手段,具有形象生动、方便灵活、深入浅出等特点,能够增加学生的学习兴趣,提高教学效果[4]。
文章开发建设岩石地下工程数字教学平台,形象和直观地展现岩石地下工程建造过程中围岩内部应力应变变化,分析不同岩体参数、应力条件等对围岩二次应力状态的影响,并可实时显示或制成动画。本平台和传统教学方法相结合,进行优势互补,可提高学生的学习兴趣,以达到更好的教学效果。
二、岩石地下工程数字教学平台的搭建 (一) 程序选用FLAC软件是由美国ITASCA公司开发的一种有限差分程序,特别适合岩土工程问题的数值模拟[5]。软件内置多种岩土本构模型,以适应不同工程的需要,其中摩尔-库伦模型是最常用的岩土本构模型。FLAC软件可分为2D和3D两种,其中FLAC 2D采用界面化操作,并自动生成可执行代码,方便对照理解和修改,同时文中岩石地下工程问题系平面应力、应变问题,因此选用FLAC 2D作为数值模拟软件。
Mathematica是一款科学计算软件,很好地结合了数值和符号计算引擎、图形系统、编程语言、文本系统和与其他应用程序的高级链接,在大学教学中有着广泛的应用[6]。Mathematica通过简单的编程就能容易地实现岩石力学公式图形化,并通过调整公式参数,便可实时观察结果的变化,给学生留下形象直观的印象。其帮助文件功能强大,使用方便,便于学生学习使用,同时也可以应用到其他学科,提高学生数学功底。
由此,文章选择FLAC进行数值模拟,采用Mathematica进行理论公式分析,以此建立岩石地下工程数字教学平台。
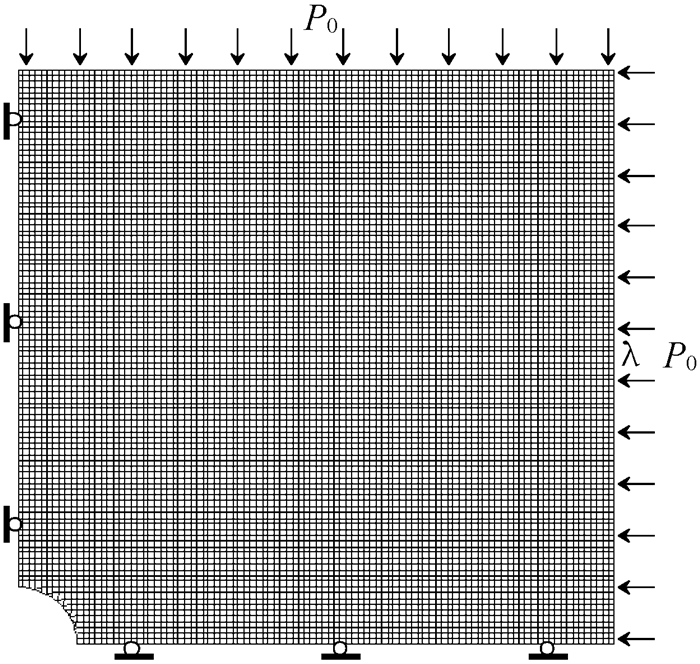
(二) FLAC模型建立文章主要研究圆形洞室岩石开挖引起的围岩应力重分布、稳定性等问题。由于所模拟圆形洞室为对称问题,为加快计算效率,取原模型的1/4进行FLAC建模,如图 1所示。圆形洞室开挖半径ra=1m,考虑边界效应问题,取边界为10倍洞室半径大小[7],即模拟区域取10m×10m范围。模型采用Build-Grid命令划分为100×100的矩形网格,再采用Alter-Shape命令将网格修改成洞室、围岩两部分。模型左边界约束X方向位移,下边界约束Y方向位移,上边界施加垂直向初始地应力P0,右边界施加水平向初始地应力λP0(λ为侧压力系数)。模型先生成初始应力,平衡后再进行洞室开挖。
|
图 1 圆形洞室FLAC模型 |
此时围岩中初始应力P0在各个方向相等,即为静水压力状态。根据静力平衡方程、几何方程和物理方程,可以求得深埋圆形洞室围岩的切向和径向应力解析解为:
| $ \left\{ {\begin{array}{*{20}{c}} {{\sigma _\theta } = {p_0}\left( {1 + \frac{{r_a^2}}{{{r^2}}}} \right)} \\ {{\sigma _r} = {p_0}\left( {1 - \frac{{r_a^2}}{{{r^2}}}} \right)} \end{array}} \right. $ | (1) |
式中,σθ、σr为极坐标下的切向应力和径向应力;ra为洞室半径;r为径向距离;P0为初始应力。
采用上述建立的FLAC模型和内置的弹性本构模型同样可以计算深埋圆形洞室围岩切向和径向应力分布,计算参数取值如下:侧压力系数λ=1,初始应力p0=-100MPa,体积模量K=6.7GPa,剪切模量G=4.0GPa。洞室开挖后围岩的二次应力状态如图 2所示,最大、最小主应力分布对应σθ和σr。从图中可以直观地发现应力呈环状分布,在同一个圆环上的应力是相等的,σθ和σr大小与径向距离r有关,而与径向夹角θ无关。洞室开挖后σθ随着r的增大呈现减小趋势,σr随着r的增大呈现增大趋势,二者最终均趋近初始应力状态,这与理论公式反映的规律一致。由于大脑对图形及颜色信息处理能力强,因此数值模拟能够增强学生对理论公式的理解,加深记忆。

|
图 2 弹性状态二次应力分布 |
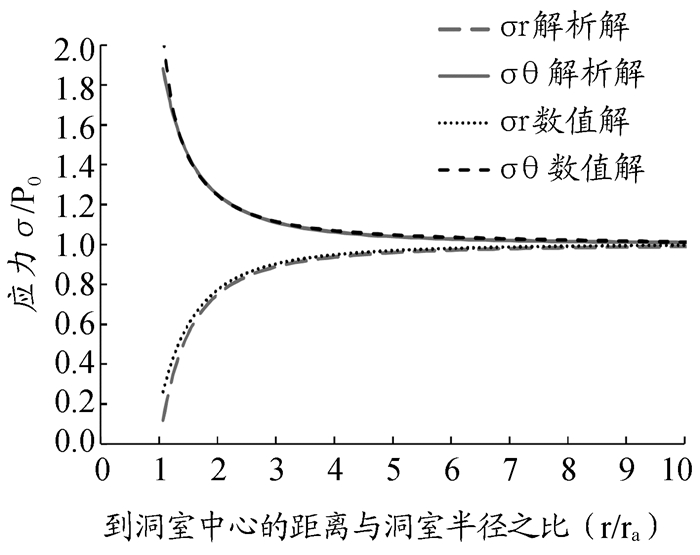
通过采用FLAC的内置FISH语言进行编程导出围岩内应力比σθ/p0、σr/p0随径向距离变化r/ra的曲线图,并与理论解析解进行对比,如图 3所示。由图可见,数值模拟结果与理论解析解基本一致,从图中可知切向正应力σθ在洞壁处最大为2p0,其随径向距离r的增大而减小,并趋于p0;径向正应力σr在洞壁处最小为0,其随径向距离r的增大而增大,并趋于p0。这个结果证明了数值模拟结果的可信性以及采用FLAC进行课堂辅助教学的可行性。
|
图 3 弹性状态应力随径向距离变化曲线图 |
通过叠加原理可以求得围岩中二次应力的弹性力学解析解。在r=ra时(即洞壁处)的切向和径向应力解析解为:
| $ \left\{ {\begin{array}{*{20}{c}} {{\sigma _\theta } = {p_0}[(1 + 2\rm{cos}2\theta ) + \lambda (1-2\rm{cos}2\theta )]} \\ {{\sigma _r} = 0} \end{array}} \right. $ | (2) |
令K=(1+2cos2θ)+λ(1-2cos2θ),则σθ=Kp0,其中K称为开挖后围岩总应力集中系数。从总应力集中系数公式可知K与θ角及侧压力系数λ有关,但很难理解这两个因素对K会产生什么影响,教材中为便于学生理解给出几个特定的λ值的K分布曲线,但是难以表现λ变化对K影响的动态变化过程。
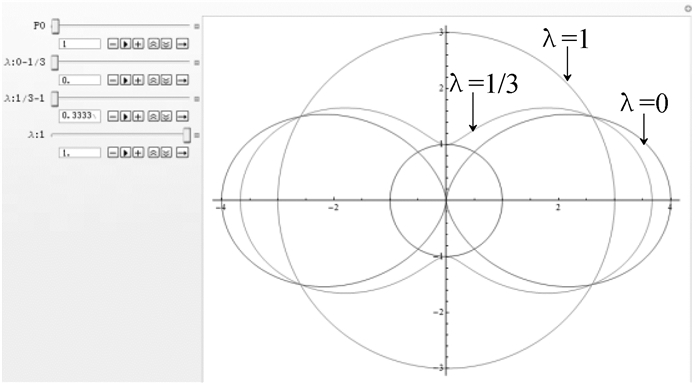
文章采用Mathematica对公式(2) 进行解析,输入公式并通过简单的命令便可绘出如图 4所示洞壁总应力集中系数变化图,其中曲线上的点沿θ方向到半径为1的圆的距离总应力集中系数值。可以通过左侧滑块及输入框动态调节一个或多个参数,直接观察图形的变化,使学生更加清晰明了地理解公式中参数变化对K值的影响。
|
图 4 洞壁总应力集中系数可视化界面 |
侧压力系数λ=1时,由弹塑性理论可求得深埋圆形洞室围岩的二次应力分为塑性区应力和弹性区应力两种状态。
塑性区应力为:
| $ \left\{ {\begin{array}{*{20}{c}} {{\sigma _{\theta p}} = \frac{{{\sigma _c}}}{{\xi - 1}}\left[{\xi {{\left( {\frac{r}{{{r_a}}}} \right)}^{\xi-1}}-1} \right]} \\ {{\sigma _{rp}} = \frac{{{\sigma _c}}}{{\xi - 1}}\left[{\xi {{\left( {\frac{r}{{{r_a}}}} \right)}^{\xi-1}}-1} \right]} \end{array}} \right. $ | (3) |
塑性区以外的弹性区应力为:
| $ \left\{ {\begin{array}{*{20}{c}} {{\sigma _{\theta e}} = {p_0}\left( {1 + \frac{{R_p^2}}{{{r^2}}}} \right) - {\sigma _{R0}}\frac{{R_p^2}}{{{r^2}}}} \\ {{\sigma _{re}} = {p_0}\left( {1 - \frac{{R_p^2}}{{{r^2}}}} \right) - {\sigma _{R0}}\frac{{R_p^2}}{{{r^2}}}} \end{array}} \right. $ | (4) |
塑性区半径为:
| $ {R_p} = {r_a}{\left[{\frac{{2{p_0}(\xi-1) + 2{\sigma _c}}}{{{\sigma _c}(\xi + 1)}}} \right]^{\frac{1}{{\xi - 1}}}} $ | (5) |
式中,
采用FLAC模型和内置摩尔-库伦理想弹塑性本构模型计算弹、塑性区二次应力分布,计算参数取值如下:λ=1,p0=-100MPa,K=6.7GPa,G=4.0GPa,c=3.45MPa,

|
图 5 弹塑性状态二次应力分布 |
|
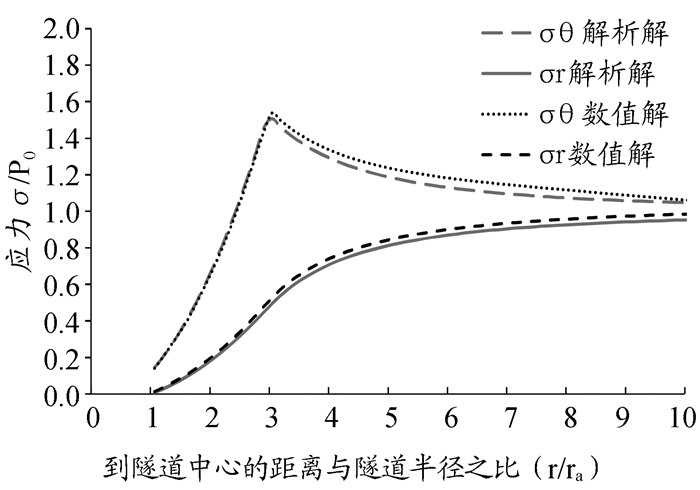
图 6 弹塑性状态应力随径向距离变化曲线图 |
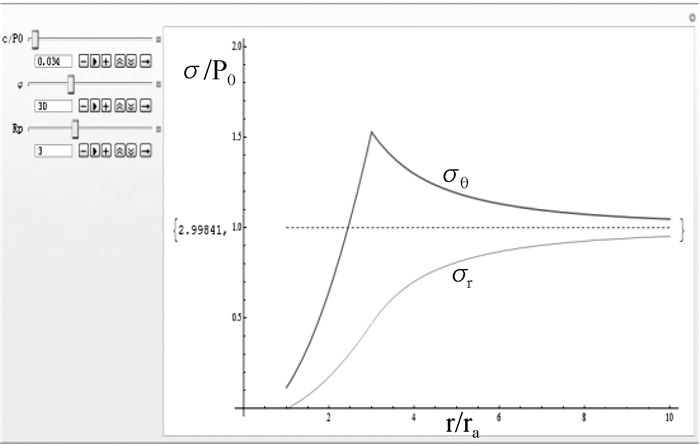
采用Mathematica编写公式(4) 和(5),并用绘图功能生成如图 7所示的可视化界面,这样可以得到不同岩体力学参数下围岩弹、塑性区二次应力分布,并可得到塑性区半径Rp。
|
图 7 弹塑性状态应力可视化界面 |
新奥法强调要对围岩尽早进行喷射混凝土初期支护,这样可保证围岩压力随初期支护刚度的逐步增大而降低,最后达到平衡状态。文章采用FLAC对新奥法施工进行模拟,为了便于分析,将支护结构的作用抽象为支护力,并沿圆形洞室洞壁均匀分布。通过控制支护力增加速率来模拟支护刚度和支护时间对围岩应力重分布的影响。FLAC模拟采用摩尔-库伦弹塑性本构模型,围岩力学参数同上,在洞室洞壁分步施加20MPa的支护力,如图 8所示,其中

|
图 8 不同支护情况下弹塑性状态应力分布 |
如图 8所示,随着支护力完成速率的减慢,围岩中的切向应力σθ的峰值先降低后增加,说明当洞室开挖完成后立即施加刚度较大的支护结构(对应
文章通过有限差分程序FLAC和科学计算软件Mathematica建立了岩石地下工程数字教学辅助平台,弥补了岩石力学传统教学的不足。该平台通过实时模拟和可视化处理方式展现了岩石地下工程开挖引起的二次应力分布,以及围岩力学参数对二次应力分布的影响,并探讨了新奥法施工中支护时间和刚度对围岩压力的影响。该教学平台丰富了教学形式,这对提高学生学习兴趣、加深理论知识理解和拓展数值分析能力具有重要意义。
| [1] | 沈明荣, 陈建峰. 岩体力学[M]. 上海: 同济大学出版社, 2006. |
| [2] | 陈建峰, 许铁欧, 俞松波, 沈明荣. 岩石三轴压缩强度实验教学改革研究[J]. 高等建筑教育, 2012, 21(1): 103–106. |
| [3] | 王子才. 仿真技术发展及应用[J]. 中国工程科学, 2003(2): 40–44. |
| [4] | 王海, 李波. 虚拟仿真技术在职业教育实践性教学环节中的应用[J]. 中国职业技术教育, 2011, 14: 48–51. |
| [5] | 陈育民, 徐鼎平. FLAC/FLAC 3D基础与工程实例[M]. 北京: 水利水电出版社, 2009. |
| [6] | 刘兴元, 何宜军. Mathematica软件的绘图功能在高等数学教学中应用示例[J]. 邵阳学院学报:自然科学版, 2008(4): 41–44. |
| [7] | 王宏辉, 张仙义. 基于FLAC 3D的圆形隧道应力位移的数值模拟与分析[J]. 工程建设与设计, 2008, 02: 73–78. DOI:10.3969/j.issn.1007-9467.2008.08.022 |
 2014, Vol. 23
2014, Vol. 23


