结构力学课程是土建、水利、力学等专业的一门重要的学科基础课,而位移法这部分内容又是结构力学课程教学的重中之重[1]。学生能否快速而准确地利用位移法进行结构分析,不仅可以检验他们对前面已学各章节知识点(包括静定结构的受力分析、力法等)的掌握程度,而且对他们后续各章节(包括渐进法、矩阵位移法、动力学基础)内容的学习效果有很大影响,是学习后续相关知识的基础[2]。笔者认为,学生在试卷上的失分点正是教学中的重难点。本文通过一次结构力学课程考试的分析与反思,总结出学生在利用位移法解题时所遇到的普遍问题,提出了一套克服这一问题的解题技巧,以供相关专业师生参考。
一、 难点探寻通过基本体系建立位移法基本方程是绝大多数院校结构力学课程教学大纲要求必须掌握的内容。基于基本体系的位移法解题步骤是:(1)加入附加约束,阻止刚结点的转动和各结点的移动,得到一个由单跨超静定梁的组合体作为基本结构;(2)使基本结构承受原来的荷载,并令附加约束发生与原结构相同的位移,得到基本体系;(3)根据基本体系附加约束上的约束力矩或约束力等于零的条件,建立位移法基本方程;(4)解算位移法基本方程,求出基本求知量;(5)按叠加法绘制弯矩图[3]。
上述解题步骤具有很强的程式化特性,只要按部就班地推进,就能得到正确的计算结果。然而,从近年来的课程考试、专业竞赛和考研的情况来看,学生们对基于基本体系的位移法掌握得并不理想。以笔者所在学校武汉工程大学2013-2014学年第一学期结构力学课程考试为例,参试的91名学生在分值为15分的位移法计算题中的整体得分率最低,仅有6名学生15分。该题原题是:用位移法求图示结构(见图 1)的M图,各杆抗弯刚度均为EI。
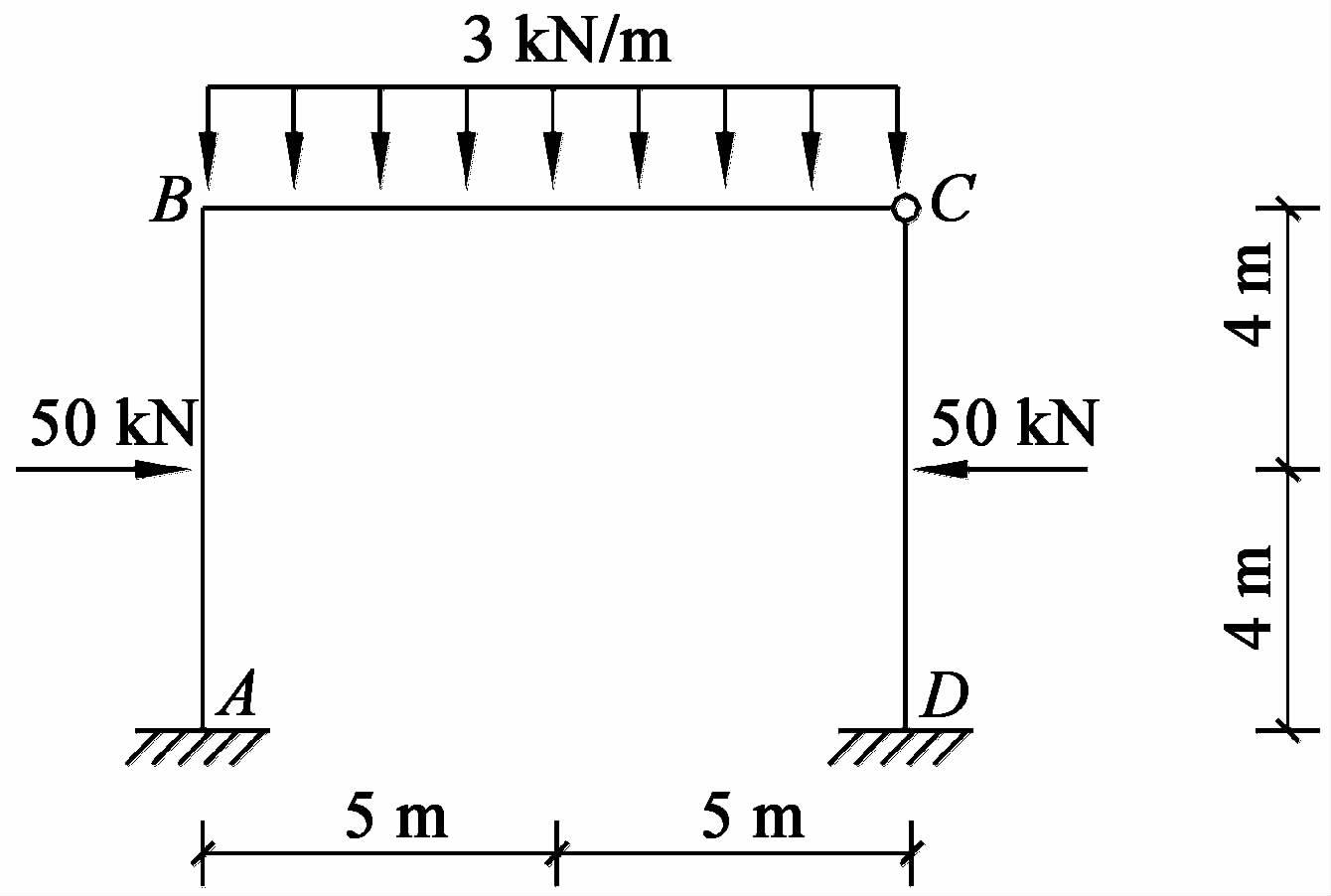
|
图 1 某刚架计算图示 |
遵循“按步骤给分”的原则阅卷后,笔者对该题各计算步骤的分值和学生的得分情况进行了统计,统计结果见图 2和图 3。
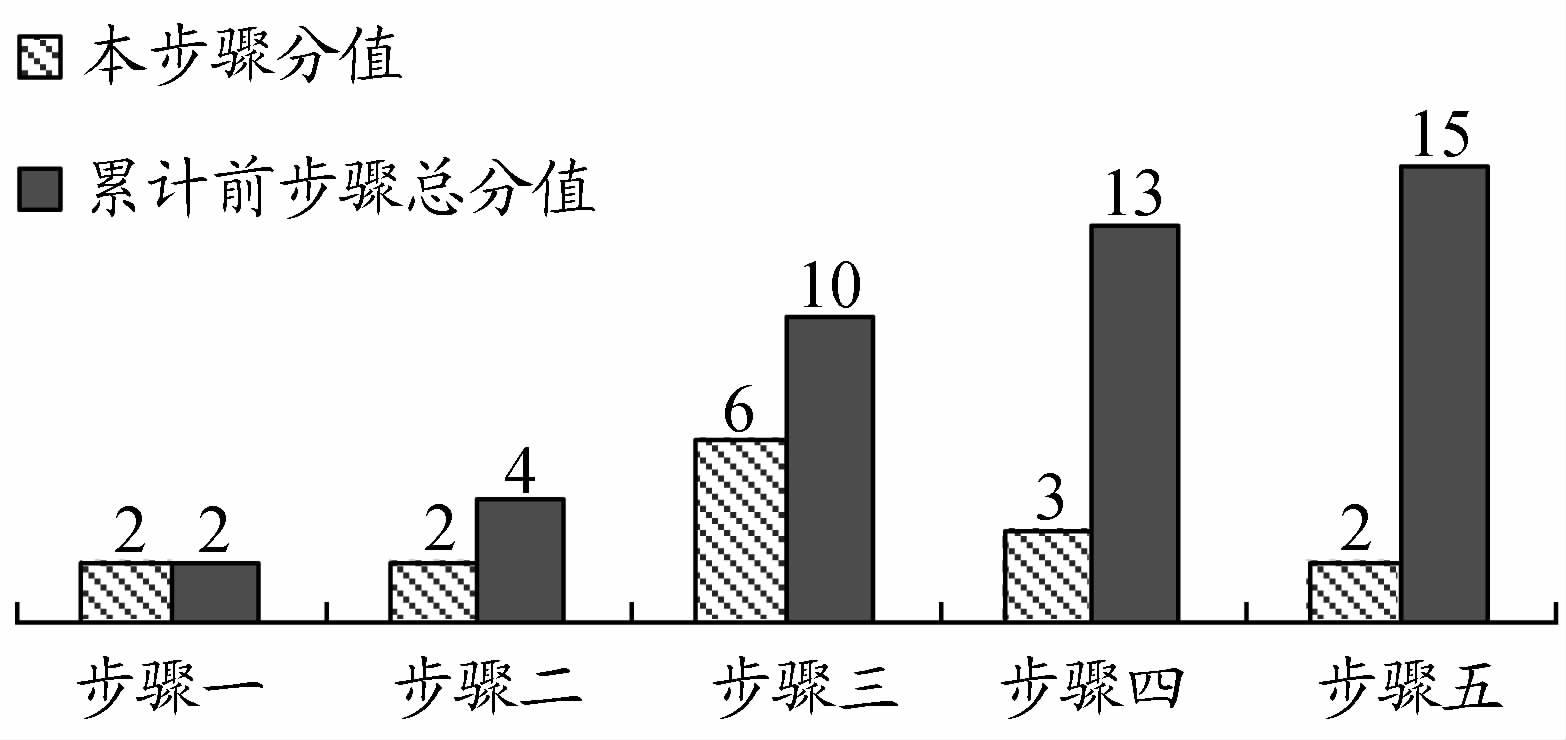
|
图 2 各步骤分值分布统计 |
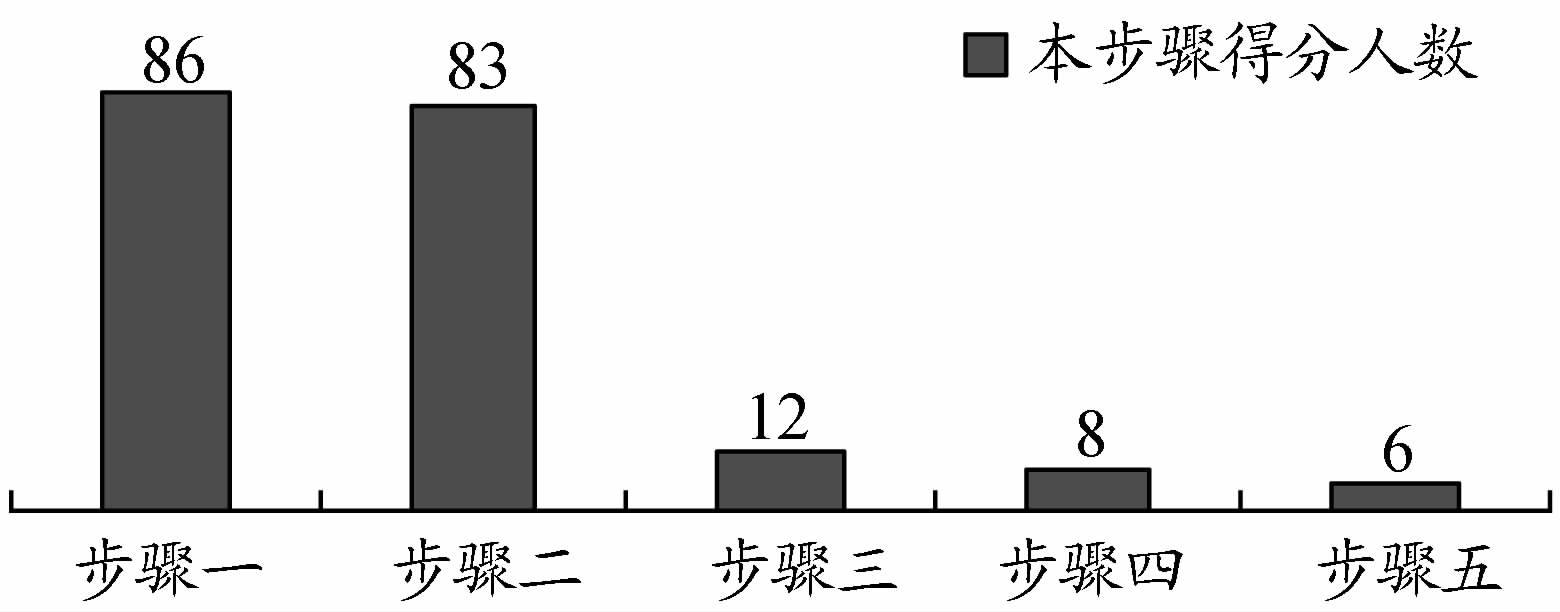
|
图 3 各步骤得分人数统计 |
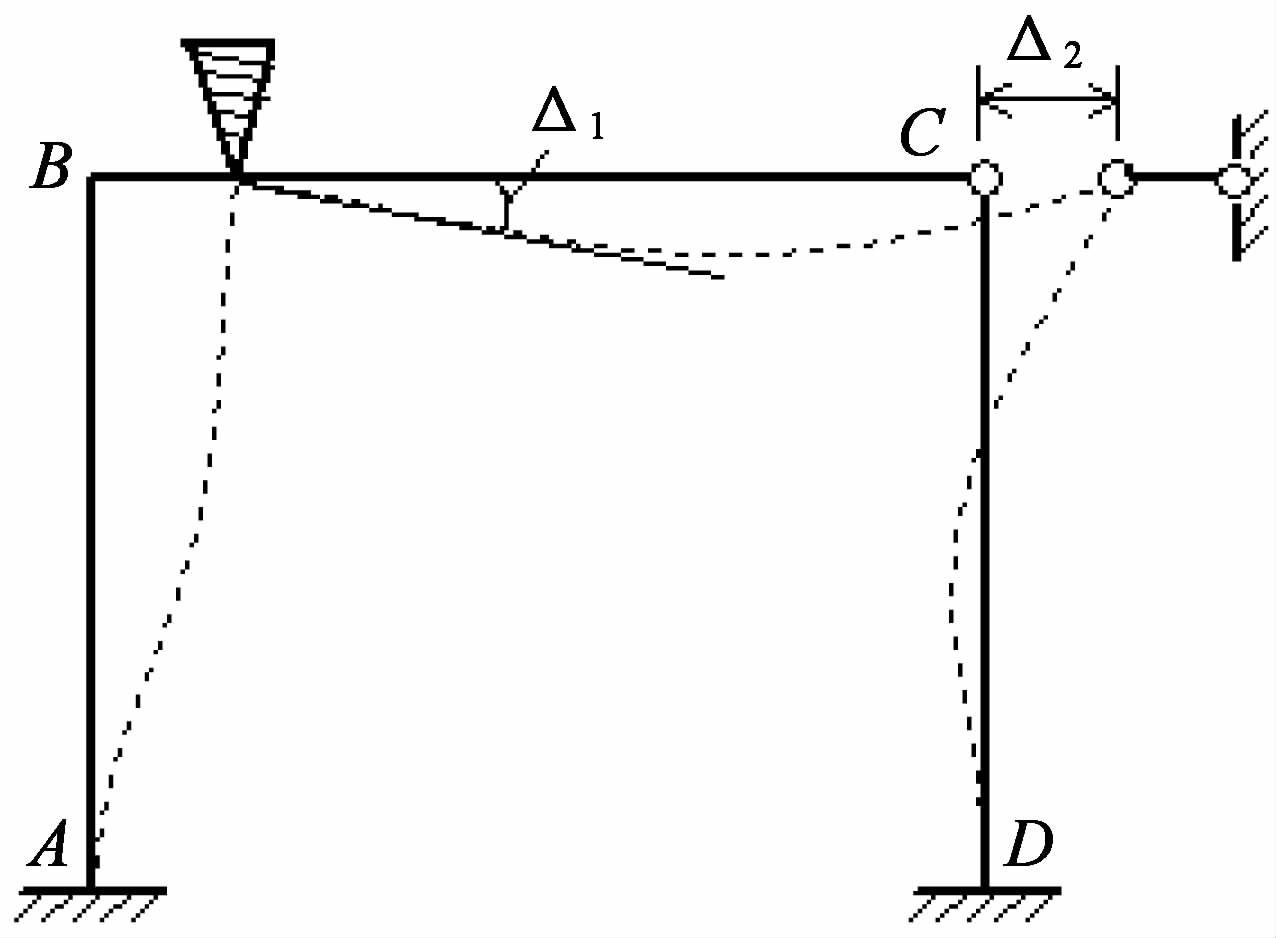
由统计结果可以看到,绝大部分学生可以正确识别基本未知量的个数,并得到基本结构和基本体系(见图 4),即能顺利完成步骤一和步骤二。但在能够完成步骤二的83名学生中,仅有12名能够完成步骤三,即正确建立位移法基本方程。在这12名学生中,又只有8名学生能够正确解得基本未知量,即完成步骤四。这8名学生中又仅有6名能够正确绘制出弯矩图,即完成步骤五,进而圆满求解该题,拿够满分15分。
|
图 4 位移法基本体系 |
笔者对部分考试失利的学生进行了试后调查。在受访的10名学生中,有9人确认能够理解通过基本体系建立位移法基本方程的基本原理;在这9人中又有7人认为自己可以快速写出具有两个基本未知量的位移法基本方程组 ,并能理解方程组中刚度系数和自由项的力学含义。但受访的10名学生均表示,在求刚度系数k11、k12、k21和k22以及自由项F1P和F2P时,这些量的符号的判断与选用成为困扰他们的因素。他们不知道作为矢量的刚度系数和自由项究竟是以顺时针为正,还是以逆时针为正,或究竟是以水平向左为正,还是以水平向右为正。
| {k11Δ1+k12+F1P=0k21Δ1+k22+F2P=0 | (1) |
显然,式(1)中的4个刚度系数和2个自由项总共6个量中,任意一个求错了,即使错了一个符号,都会导致基本未知量Δ1和Δ2无法正确计算,最终前功尽弃。因此,不能准确求得位移法基本方程中的刚度系数和自由项是学生运用位移法解题的难点所在。
在目前使用甚广的一些经典结构力学课程教材中,结点转角、弦转角、杆端弯矩等矢量均以顺时针为正,但没有对附加约束力(或约束力矩)的正负作规定[3-4],使得学生在构建位移法基本方程组时遇到刚度系数和自由项符号混乱的问题。如果能将符号混乱的问题解决好,上述运用位移法解题的难点就可以得到解决。
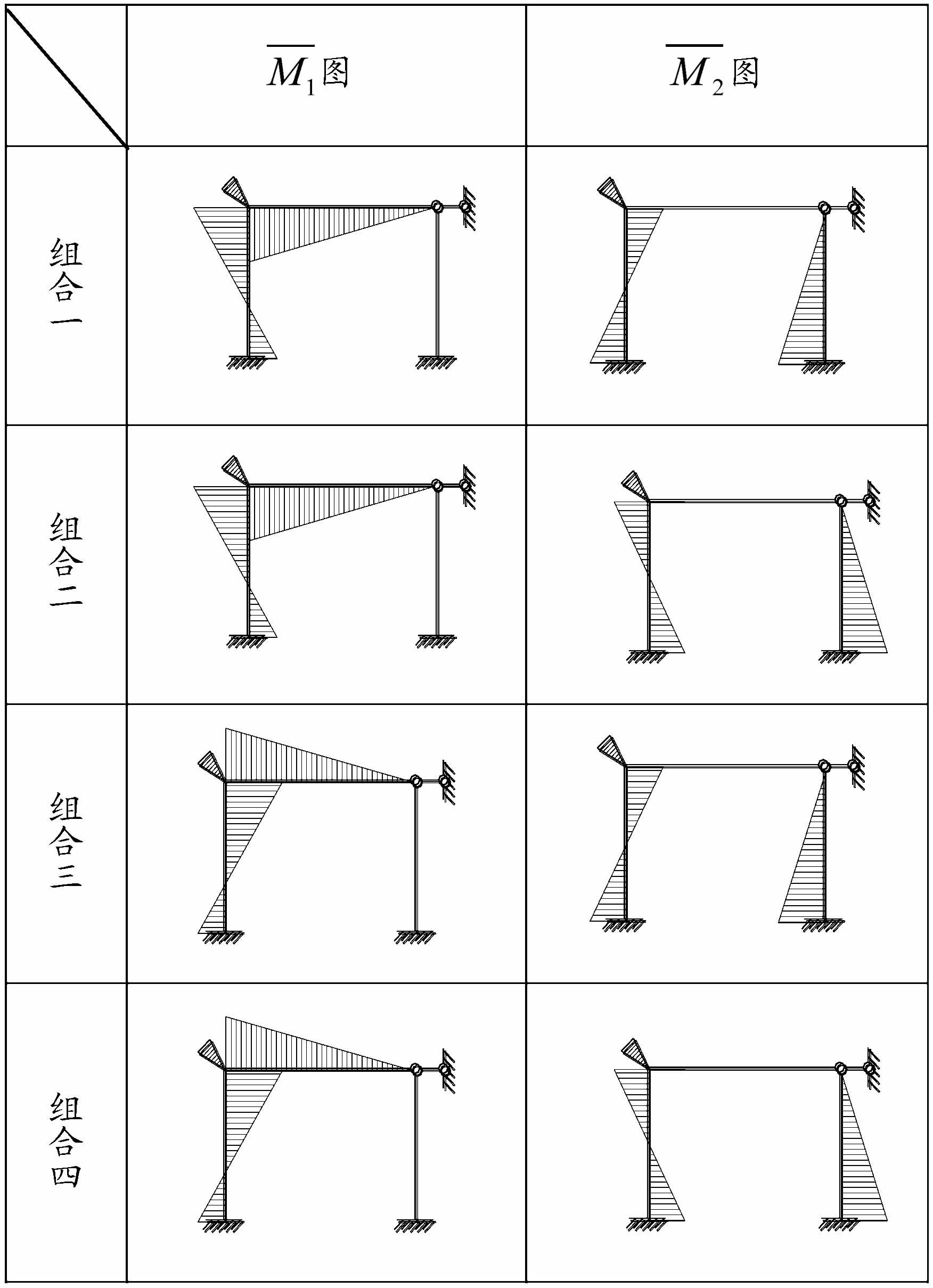
二、 难点攻克上述考题涉及超静定结构是有侧移的刚架,具有结点转角和线位移两种基本未知量,颇有代表性。本文以该题的解答为例,提出一套避免刚度系数和自由项符号发生混乱的解题规则,以指导学生凭借该规则准确建立位移法基本方程。这套规则有以下两个方面的内容。
(一) 规定附加约束单位角位移和线位移的参考方向在令Δ1=1且Δ2=0进而求刚度系数k11和k21时,Δ1对应的附加约束(图 4中B结点处的刚臂)所发生的单位转角位移,可以假设发生在顺时针方向上(
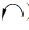
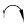
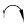
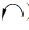
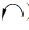
| 表 1 附加约束发生单位位移时基本结构可能产生的M图 |
需要指出的是,在计算刚度系数之前,选择上述四种方向组合中的任意一组作为附加约束单位角位移和线位移的参考方向都是可行的。但附加约束单位角位移和线位移的参考方向一经选定,在后续计算刚度系数的过程中就不可改变,否则会导致刚度系数的符号出错。在求解上述题目的过程中,本文拟假设附加刚臂约束的单位角位移发生在顺时针方向上,附加链杆约束的单位线位移水平向右,亦即基本结构的M1 图和M2 图与表 1中基本未知量参考方向的组合一相对应。
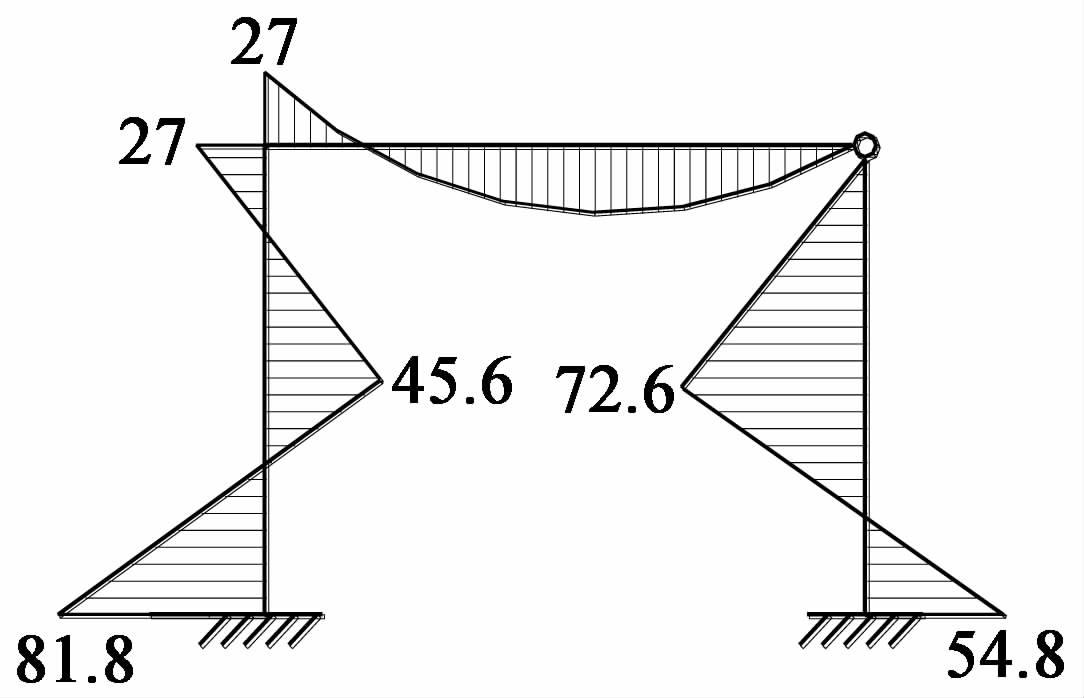
(二) 规定附加约束上约束力矩和约束力的参考方向在规定了附加约束单位角位移和线位移的参考方向之后,就可以进行刚度系数k11、k12、k21、k22以及自由项F1P和F2P的计算了。根据图 5给出的隔离体受力平衡分析图,可由隔离体所受力或力矩的平衡方程求解出各刚度系数和自由项来,求解过程见式(2)至式(7)。
| k11−3iBC−4iAB=0⇒3iBC+4iAB | (2) |
| k12−0+6iABlAB=0⇒k12=6iABlAB | (3) |
| F1P+ql2BC8−qlAB8=0⇒F1P=qlAB8−ql2BC8 | (4) |
| k21+0+6iABlAB=0⇒k21=6iABlAB | (5) |
| k22−3iCDl2CD+12iABl2AB=0⇒k22=3iCDl2CD+12iABl2AB | (6) |
| F2P+5F16+F2=0⇒F2P=−3F16 | (7) |
|
图 5 用于求解刚度系数与自由项的隔离体受力图 |
令EI/8m= i ,则iAB=iCD=5i,iBC=4i。将iAB=iCD=5i,iBC=4i,lAB=lCD=8m,lBC=10m,q =3kN/m,F =50kN代入式(2)至式(7),便可得到各刚度系数和自由项的具体数值,再将这些具体数值代入位移法基本方程组即式(1),并解该方程组,得到
| Δ1=78i,Δ2=545i |
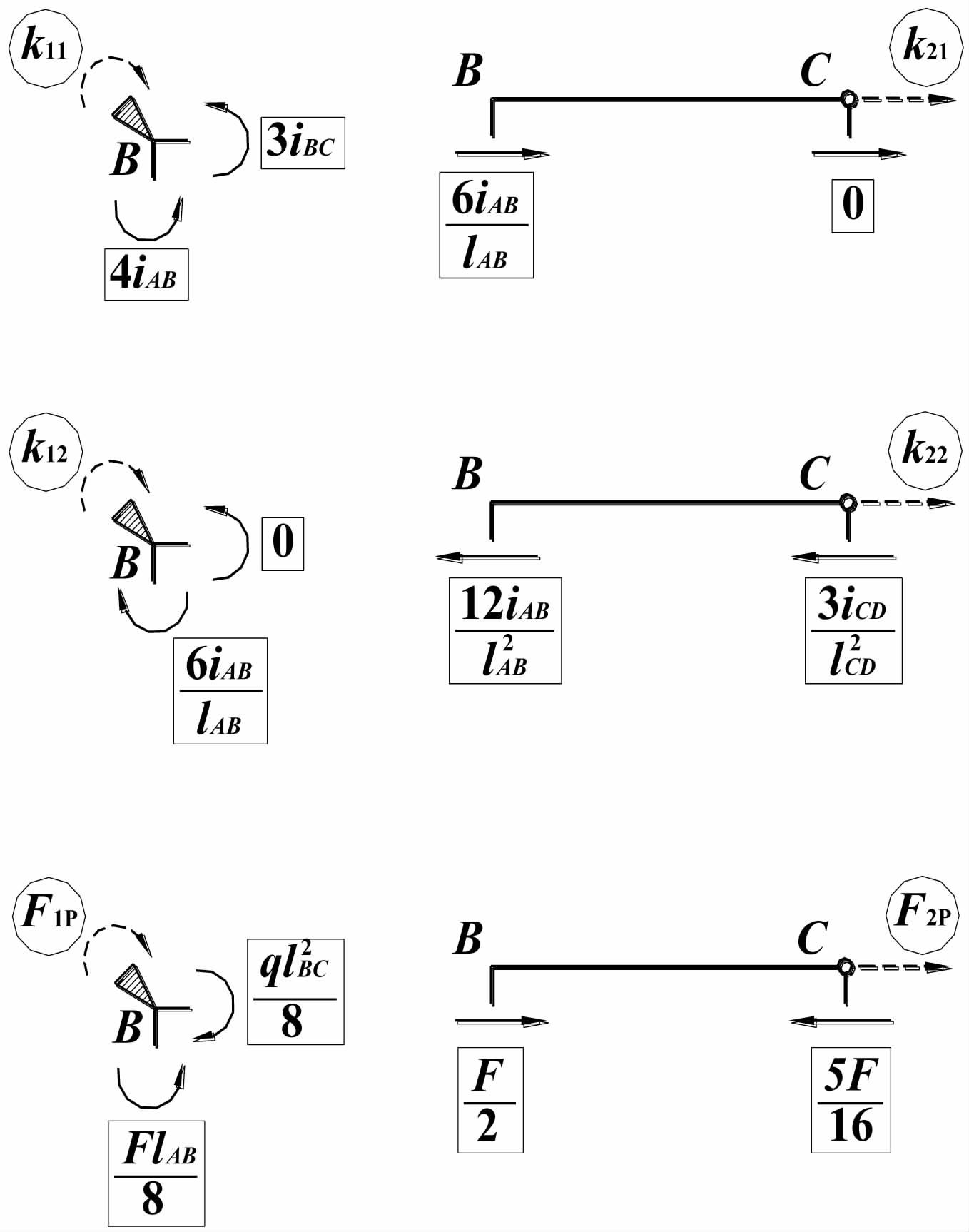
最后,根据叠加法,由M1 Δ1+M2 Δ2+MF绘制原结构的弯矩图(见图 6)。
|
图 6 原结构M图(单位:kN·m) |
上述计算刚度系数和自由项的过程虽然顺理成章,但其中隐藏着符号的规定。如果学生对此符号的规定认识模糊,就很有可能不能准确计算刚度系数和自由项。为了把这里的符号规定表达清楚,本文特用圆圈和矩形框区别图 5中的矢量,用实线和虚线区别这些矢量的标线。具体来说,图 5中被矩形框标示的矢量的大小均为各杆件形常数或载常数的绝对值,它们的方向均由前述附加约束的单位位移的参考方向所决定,矢量标线均用实线表示。图 5中被圆圈标示的矢量是附加约束上的约束力或约束力矩,矢量标线均用虚线表示。从力学含义上来看,k11、k12、F1P均为附加刚臂上的约束力矩,k21、k22、F2P均为附加水平链杆中的约束力,不少学生在解题时往往不知将k11、k12、F1P的参考方向定为顺时针合适,还是定为逆时针合适,也不知将k21、k22、F2P的参考方向定为水平向左合适,还是水平向右合适,最终将k11、k12、F1P或k21、k22、F2P三者的参考方向定得不一致,即其中一个的方向与其余两个的相反,这必将导致Δ1和Δ2的计算错误。
显然,将k11、k12、F1P三者的参考方向设置得一致的做法有两种,即要么都设为顺时针方向,要么都设置为逆时针方向;将k21、k22、F2P三者的参考方向设置得一致的做法也有两种,要么都设为水平向右,要么都设为水平向左。这样一来,关于附加约束上的约束力(或约束力矩)方向的假设也会出现四种可采用的组合(见图 7)。
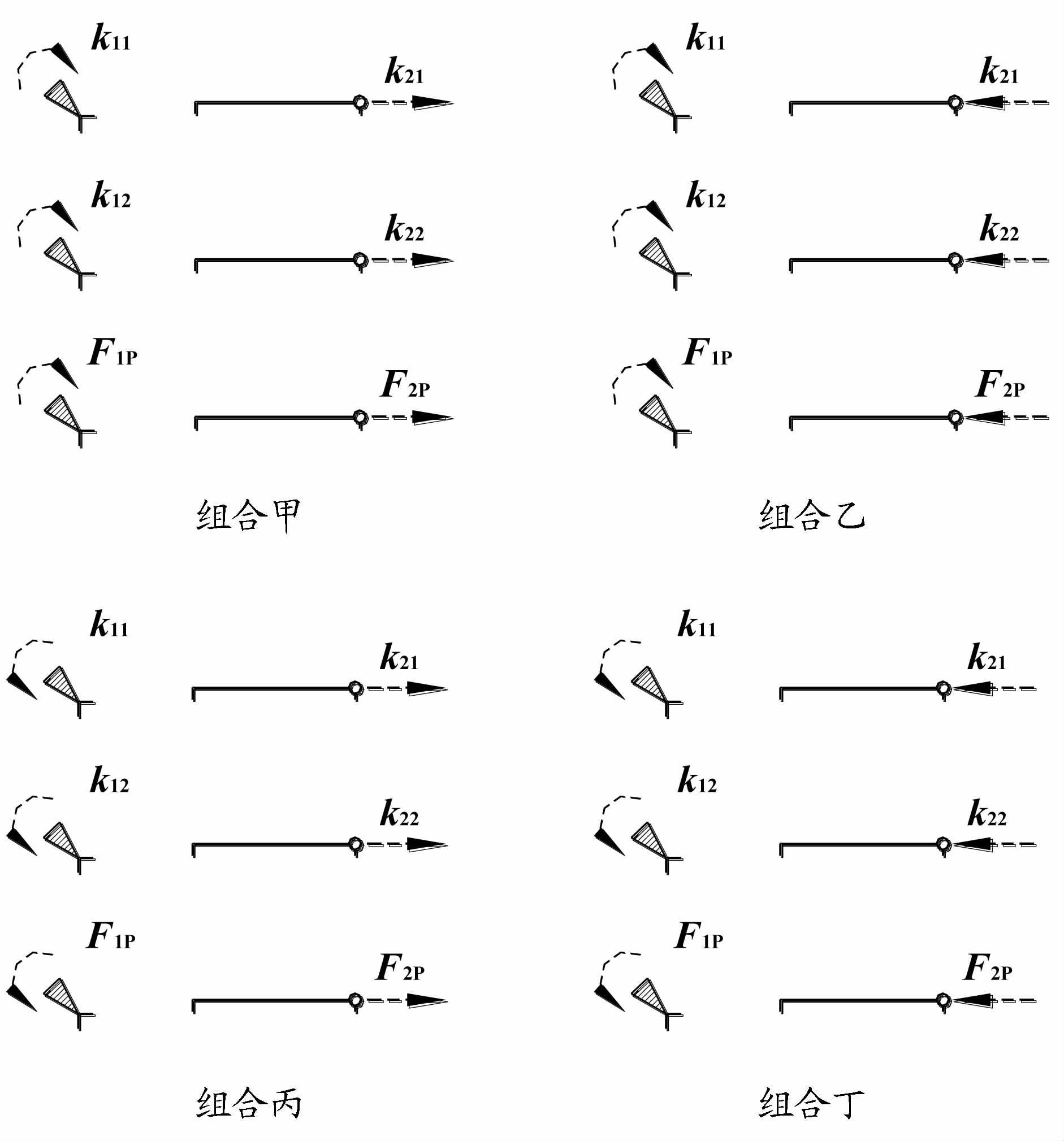
|
图 7 附加约束上约束力矩和约束力参考方向可采用的组合 |
从图 5可以看到,在前述刚度系数和自由项的计算过程中,附加约束上约束力矩和约束力的参考方向采用的是图 7中的组合甲。如果把组合甲对应代入刚度系数和自由项具体数值的基本方程记为式(1),那么与组合乙、丙、丁对应的代入刚度系数和自由项具体数值的基本方程将呈现式(8)、(9)、(10)的形式。
| {k11Δ1+k12+F1P=0−k21Δ1−k22−F2P=0 | (8) |
| {−k11Δ1−k12−F1P=0k21Δ1+k22+F2P=0 | (9) |
| {−k11Δ1−k12−F1P=0−k21Δ1−k22−F2P=0 | (10) |
显然,方程(8)、(9)、(10)的解与方程(1)的完全相同,均为:
| Δ1=78i,Δ2=545i |
从数学的角度看,这种基本未知量求解结果在图 7所示附加约束上约束力矩和约束力参考方向的四种组合情况下不发生改变的现象,可以用线性方程组的增广矩阵作线性变换后方程组的解不变的特性来解释。
三、 延伸思考可以看到,列出位移法基本方程的过程就是对基本体系附加约束上的若干约束力求和,并令此和为零的过程。这里的若干约束力之和从本质上讲是若干共线矢量之和,而对共线矢量求和是必须在一定的参考方向下实施的,所以参考方向的规定十分重要。必须指出,参考方向一经规定,解题中就不可再改变,否则极易导致刚度系数和自由项被计算错误。
在用基于基本体系的位移法求解超静定结构时,如果基本未知量的个数达到两个或两个以上,矢量参考方向就存在多种组合。一般而言,附加约束单位位移的参考方向一经确定,基本方程的解在每个附加约束上约束力的参考方向设置一致的前提条件下,不随其组合的改变而改变(其数学背景已在上文中说明)。另外,附加约束单位位移参考方向组合有多种,在每种组合下,基本方程的解只存在符号上的差别,最终得到的M图不因这种差别而改变。以本文例题为例,附加约束单位位移的参考方向有四种组合,附加约束上约束力的参考方向组合也有四种组合,故此题在不同参考方向体系下的解题路径共有16条,但最终得到的M图有且仅有一个,可谓殊途同归。图 8将位移法的这种特点展现了出来。
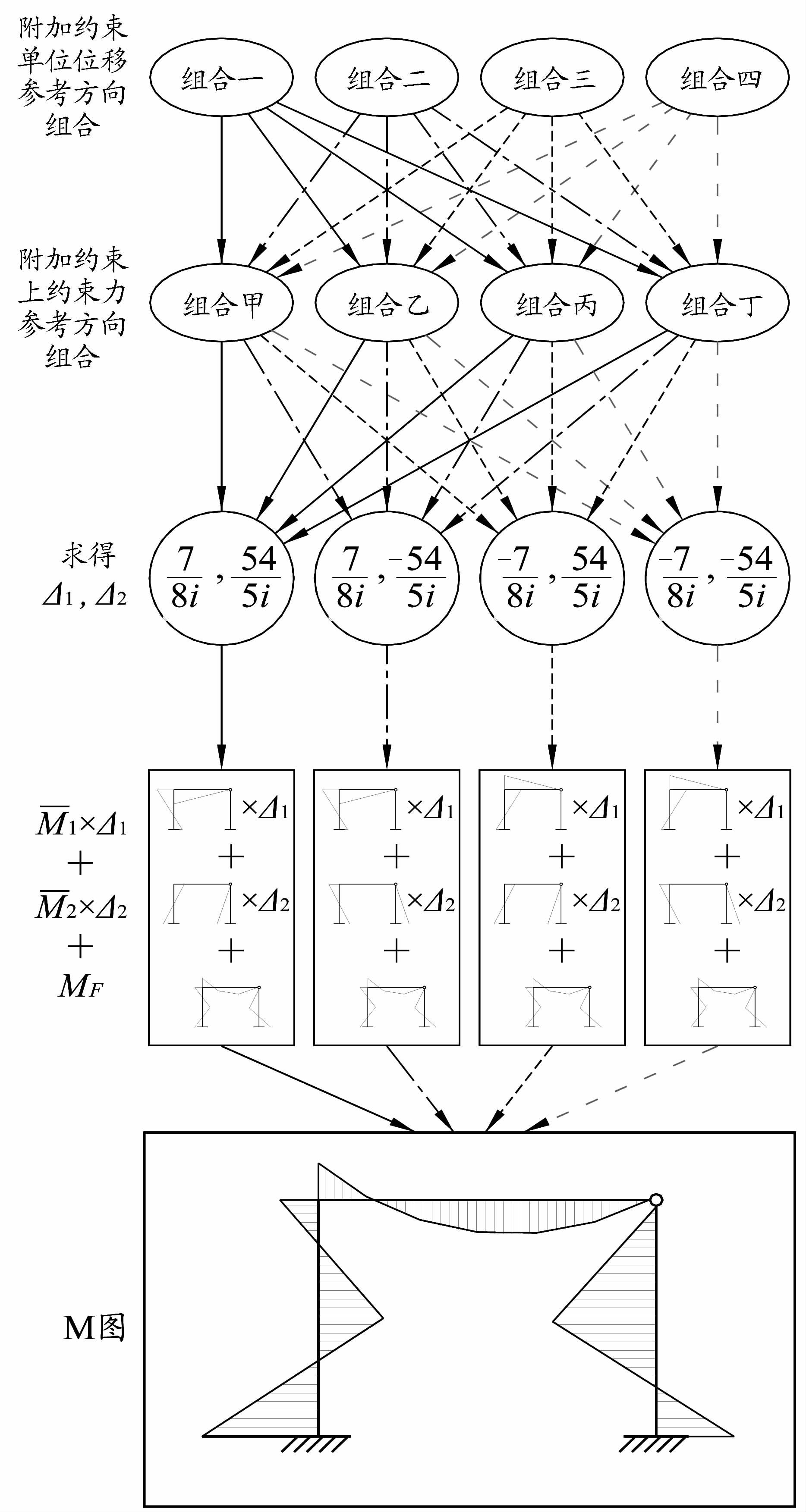
|
图 8 不同参考方向组合下的解题路径 |
(1) 通过“按步骤给分”的命题和阅卷方式、筛分式的卷面分析法以及对考试失利学生进行试后访谈,可以找到学生所遇到的解题难点和学习障碍。
(2) 结构力学教材对附加约束的单位位移和约束力的符号未作规定,导致学生在采用基于基本体系的位移法解题时,容易因“符号混乱问题”而将基本方程中的刚度系数和自由项求错,这是学生解答该类问题时普遍遇到的难点。
(3) 对于有两个及两个以上基本未知量的位移法计算题,只要确保在整个解题过程中附加约束单位位移的参考方向不改变,每个附加约束上约束力的参考方向设置得一致且不改变,就能够避免上述将基本方程中的刚度系数和自由项求错的问题。
总之,结构力学课程任课教师应在教学过程中,将符号规定及其在解题过程中所产生的影响讲深讲透,加深学生对符号问题的认识,同时要求学生减少解题出错的几率。
| [1] | 李国华, 罗健, 董军, 戚承志. 结构力学教学方法研究[J]. 高等建筑教育 , 2012, 21 (1) : 81–83. |
| [2] | 朱少云. 位移法典型方程的取舍对结构力学教学的影响[J]. 力学与实践 , 2000, 22 (4) : 50–51. |
| [3] | 龙驭球, 包世华, 袁驷. 结构力学I—基本教程[M]. 北京: 高等教育出版社, 2012 . |
| [4] | 龙驭球, 包世华, 袁驷. 结构力学I—基本教程[M]. 北京: 高等教育出版社, 2012 . |
| [5] | 朱慈勉, 张伟平. 结构力学:上册[M]. 北京: 高等教育出版社, 200 . |
 2015, Vol. 24
2015, Vol. 24