目前, 各高校在本科教育阶段都非常注重对创新人才的培养, 而科研训练是推动创新人才成长的驱动力, 因此, 通过选择合适的课程对学生进行一定的科研训练无疑对人才培养的质量起着重要的促进作用。
土力学是研究土体的应力、变形、强度、渗流及长期稳定性的一门学科。其很多课程内容和研究方法均借鉴于其他的力学学科。例如, 土中应力计算来源于弹性力学中的布辛奈斯克(Boussinesq) 解, 土中的渗流计算源于流体力学, 土中的应力状态和挡土墙土压力计算来自于材料力学中的强度理论, 地基的极限承载力计算源于塑性力学中的滑移线理论。因此, 通过对土力学的学习, 学生除了可以更加深入地理解相关力学知识外, 还可以学会如何用一般的力学原理来解决实际工程问题。
另外, 除了具有深厚的理论背景外, 土力学还是一门实践性较强的课程。事实上, 作为土力学的研究对象, 土是一种非均质、非弹性、多孔的三相介质, 与以往的各种力学学科所研究的对象有着本质的区别。因此, 在沿用以往力学知识的同时, 须借助于配套的参数获取方法和工程经验的辅助, 才能使以往建立在理想介质基础上的力学知识适用于土这种复杂的多孔介质。因此, 土力学是一门理论结合实践的综合性课程, 非常适合用来训练和培养学生的科研能力。
因此, 土力学一直是高校教师进行教学改革尝试的热点课程, 也取得了显著的教学效果[1-3]。文章以土力学中应力历史知识点的授课为例, 通过采用设置问题的方法帮助学生理解知识, 同时在掌握知识的基础上, 通过对知识点的引申, 使学生了解与所学知识点相关的学科前沿动态, 对学生的科研素质进行启蒙, 以达到科研训练的目的。
一、 设置问题掌握知识点土层的应力历史指土层在沉积过程中(即历史上) 的受力情况, 可通过土层先期固结压力pc与现有的覆盖土重p1之比OCR来加以描述。根据应力历史可将土分为正常固结土、超固结土和欠固结土三种。对于应力历史的学习, 其首要问题是确定土层的先期固结压力pc, 只有确定了先期固结压力才能描述土层目前所处的状态。
先期固结压力是土力学中一个重要概念, 是衡量土体结构性的参数之一。教师在讲授先期固结压力时, 可按照学生的思维习惯, 将想要讲授的内容设置成一系列由浅入深的问题, 教师以问题为导向, 通过解答问题来帮助学生理解先期固结压力。在教学中笔者按照图 1所示的讲解思路, 讲授先期固结压力时所设置的问题和解答如下。
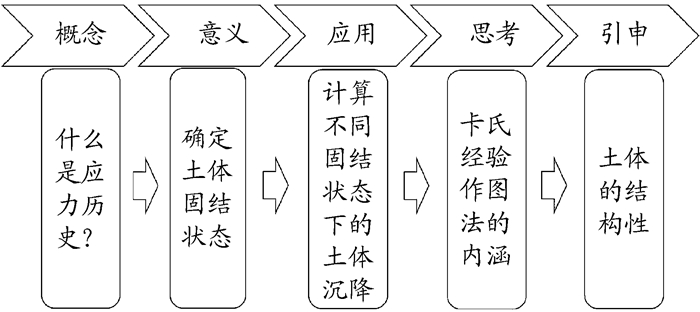
|
图 1 以应力历史为例的知识点讲解思路结构图 |
(1) 对学生来讲, 当接触一个新的知识点时, 其第一反应就是知识点概念的探知, 即讲的是什么, 因此教师的首要任务是帮助学生了解概念。因此, 教师首先给出先期固结压力的定义, 即先期固结压力是天然土层在地质历史上所经受过的最大有效应力或者固结压力。教师要指出该定义所隐含的更为深层的意义, 即先期固结压力是土层在地质历史上所经受过的最大压力; 在该压力下土层的固结已经结束, 因此, 先期固结压力也称土层在地质历史上所受到的最大竖向有效应力。
(2) 介绍完先期固结压力的概念, 学生紧接着会问:为什么要学习先期固结压力?学习这个概念有什么作用?教师应该讲述学习先期固结压力的意义, 让学生明白了学习这个知识点的意义, 学生才能对其概念有更为深刻的认识。
教师可按如下讲述:首先, 先期固结压力是反映土层原始应力状态的一个指标。通过先期固结压力pc与现有的覆盖土重p1之比可以判断土体属于超固结土、正常固结土还是欠固结土。一般来说, 同一深度处, 超固结土压缩性较低, 正常固结土次之, 欠固结土压缩性最高, 所以说, 通过先期固结压力能大概判断出土体的压缩性大小。
另外, 土体在超固结段和正常固结段的压缩性不同, 所以在计算土层的沉降时, 必须首先确定土层的先期固结压力, 以此来确定土体在不同的压力范围段内处于何种状态。以超固结土为例, 超固结土的压缩曲线在先期固结压力前、后分别处于超固结状态和正常固结状态, 两种状态采用不同的压缩性指标来计算土层沉降。因此, 先期固结压力的确定是计算土层沉降的先决条件。
(3) 紧接着给出下面的问题:既然在土体的压缩曲线上存在超固结段和正常固结段, 那这两段如何区分?也就是如何确定先期固结压力?
教师解答如下:以四校合编的《土力学》教材为例[4], 各类教材都推荐采用如图 2所示的Cassagrande经验作图法来确定先期固结压力, 首先找出e-lgp曲线上曲率半径最小的一点A; 然后过A点作水平线A1和切线A3;最后过A点作∠1A3的平分线交曲线后半段的直线段于B点, B点对应的压力即为先期固结压力pc。
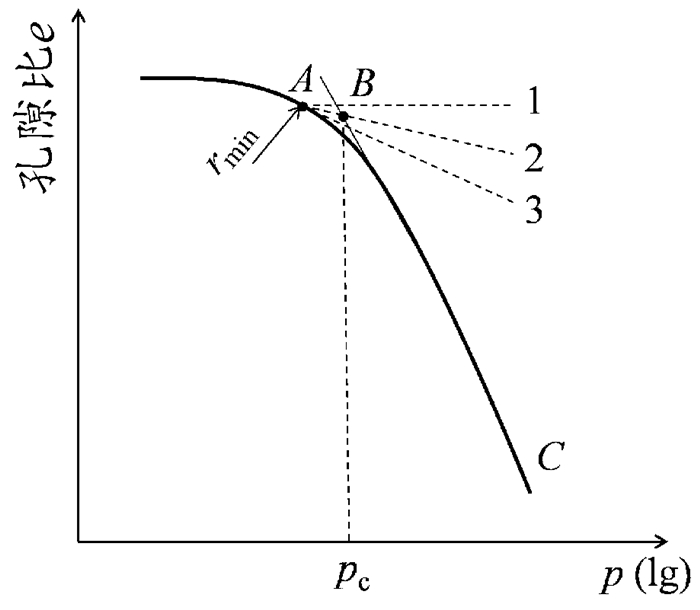
|
图 2 Cassagrande法确定先期固结压力 |
(4) 上述问题在教科书上已经讲解清楚, 教师可进一步引导学生深入思考:Cassagrande作图法虽然是一种经验作图法, 其背后有没有理论依据?如何理解该法?
对于上述问题, 可以让学生在课后思考, 待下节课上课之前解答。教师最后可以给出如下解答:Cassagrande法是在研究了许多试验曲线后归纳总结的一种经验作图法。对于扰动较小的土样, 用Cassagrande法得到的先期固结压力比较准确。目前, 各类教科书上均没有解释其背后的理论依据。实际上, Cassagrande作图法虽然是一种经验方法, 但也是基于大量的试验数据而成, 是对客观试验现象的总结, 其背后也存在着一定的理论依据。
首先, 向学生说明为什么室内压缩曲线存在曲线段。实验室中的土样一般均为现场采样, 土样在采集过程中, 之前作用在土样上的压力得以卸除, 所以土样在加载初期实际上是处于一种超固结状态, 在重新加载时必然存在一个由超固结状态向正常固结状态转变的过程。理论上讲, 如果土样在采集、运输及试验过程中不受到扰动影响, 土体的压缩曲线应该是两个直线段, 分别对应土样的超固结段和正常固结段, 两直线段的交点即为先期固结压力。然而, 试验土样难免会受到不同程度的扰动, 因此土样由超固结状态向正常固结状态转变时在压缩曲线上表现为曲线上的弯曲段。
Cassagrande法第一步所确定的A点是压缩曲线上曲率半径最小的点, 可以认为A点是土的压缩特性发生变化的转折点, Cassagrande认为先期固结压力就在该点附近, 通过A点分别作水平线A1和切线A3。水平线A1代表转折点处的孔隙比, 与直线段(即压缩曲线后半段) 的交点横坐标代表土样处于正常固结状态时压缩至该孔隙比对应的压力; 切线A3代表转折点处的回弹再压缩指数(因为处于回弹再压缩过程中), 与直线段的交点横坐标代表土样由超固结状态压缩至正常固结段时对应的压力。理论上讲, 直线段与A1和A3的交点横坐标均为先期固结压力, 因此Cassagrande采用折中的方法, 取两交点横坐标的平均值, 即∠1A3的角平分线A2与直线段交点的横坐标作为先期固结压力。所以说, Cassagrande经验作图法是有一定理论依据的。
最后向学生指出, Cassagrande经验作图法对土样和作图的比例尺均有严格的要求。首先, 要求尽可能避免在土样的采集、运输及试验过程中产生大的扰动, 事实上, 只要土样受到的扰动效应较小, 采用Cassagrande经验作图法确定的先期固结压力一般均比较准确。另外, 采用Cassagrande经验作图法时要注意绘图比例尺的选择, 否则会出现A点很难确定, 甚至A点位置随绘图比例尺而改变的问题。因此, 在确定先期固结压力时, 一般还需结合场地地形和地貌等地质资料加以判断。
二、 知识点的引申讲完应力历史的概念, 引导学生思考为什么土体在超固结段和正常固结段具有不同的压缩特性?
土体的应力历史和结构性以及土体的压缩性关系如图 3所示。广义上讲, 所有的天然土体都具有结构性, 土的结构性是指土体颗粒和孔隙的性状和排列形式, 以及颗粒间的相互作用。土的结构性产生于土体的沉积过程中, 与上覆土层的压力大小直接相关, 是土体在形成过程中所产生的固有属性。土的结构性使土体表现出具有记忆的特性, 土体可以将历史上曾经受过的固结压力, 通过结构性保持下来[5]。
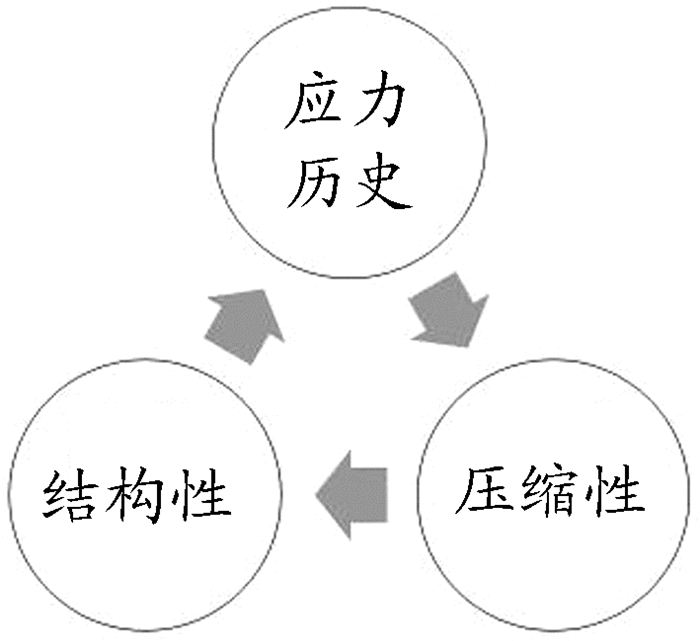
|
图 3 引申知识点和授课知识点的关系 |
土体的变形包含可以恢复的弹性变形和不可恢复的塑性变形。当土体经历卸荷作用时, 土体产生回弹变形, 回弹变形不包含塑性变形, 因此回弹曲线将会偏离压缩曲线。当对土体进行再加载时, 由于土体结构性的记忆特征, 土体的再压缩曲线会逐渐向正常压缩曲线靠拢, 因此, 在回归到正常压缩曲线之前和之后处于两种不同的压缩曲线上, 导致土体在超固结段和正常固结段压缩特性不同。
介绍完土体结构性的概念, 可以将目前学术界对土体结构性的研究内容和采用的研究方法向学生作简单介绍, 以开阔学生的科研视野, 起到科研训练的启蒙作用。
三、 结语以应力历史知识点的讲授为例, 结合笔者多年的授课经验, 阐述了在土力学授课中如何对学生的科研素质进行训练。提出了以问题为导向的知识传授方法, 并在传授知识的基础上, 进一步将知识点进行引申, 使学生了解知识点相关的学科前沿动态, 从而起到对学生的科研意识进行启蒙的作用。文中给出的教学方法对土木工程专业的其他课程有一定的借鉴作用。
| [1] | 张艳美, 杨文东, 奕雅琳, 李春宝. 基于工程问题的土力学与基础工程课程建设探索[J]. 高等建筑教育, 2016, 25(4) : 74–77. |
| [2] | 王安明, 周进, 刘娉慧, 黄志全. 基于"教、学、用"三位一体的土力学课程教学模式改革与实践[J]. 高等建筑教育, 2015, 24(4) : 52–54. |
| [3] | 熊浩. 任务驱动式教学法在土力学课程中的实践[J]. 高等建筑教育, 2014, 23(5) : 69–71. |
| [4] | 东南大学, 浙江大学, 湖南大学, 苏州科技学院合编. 土力学[M]. 北京: 中国建筑工业出版社, 2010. |
| [5] | 高大钊. 土力学与岩土工程师[M]. 北京: 人民交通出版社, 2008. |
 2017, Vol. 26
2017, Vol. 26


