2. 哈尔滨工程大学 航天与建筑工程学院, 黑龙江 哈尔滨 150001
2. College of Aerospace & Civil Engineering, Harbin Engineering University, Harbin 150001, P. R. China
随着计算机技术的发展,数值模拟已经成为结构科学研究的基本方法,也是重要的教学内容。结构动力分析是建筑抗震、抗风、抗爆以及振动控制等领域的理论基础,也是掌握结构动力性能和设计的关键内容[1]。由于该部分内容涉及时间、结构动力特征、初始条件和外部激励等变量,并且变量之间相互影响,应用数值模拟提高该部分的教学质量具有显著的意义。应用数值模拟提高教学质量是国内外大学教育的发展趋势,美国迈阿密大学S.S. Rao将MatLab与结构振动教学进行了完美的结合[2],陈清军和李文婷应用ANSYS软件探讨结构动力学的多元化教学,并取得了良好的效果[3]。应用计算机数值仿真,提高大学教学质量是发展趋势。
MatLab是矩阵(Matrix)、实验室(Laboratory)两个词的组合,称为矩阵实验室, 是由美国新墨西哥大学Cleve Moler教授为教学而开发的。MatLab的基本单位是矩阵,具有与数学分析、工程应用无缝对接的优点。MatLab已经成为科学研究、工程设计、教学仿真的良好平台。在建筑结构领域,MatLab具有良好的应用前景。徐赵东等在MatLab软件平台上,进行了建筑结构静动力、结构的振动控制分析[4]。在时域分析方面,赖伟和周至浩进行了结构动力特性、地震波的处理和结构时程反应分析[5],黄晓吉用Simulink进行了结构的时程分析[6]。李双艳等应用单位阶跃响应函数Step(.)、单位冲击响应函数Impulse()等内部函数进行了结构线性弹性分析[7]。陈力宇等应用MatLab实现了Wilson-θ法结构分析[8]。马乐为等基于脉冲频响函数,应用MatLab的卷积公式,为频域分析奠定了基础[9]。熊森等学者从传递函数角度,进行了结构动力响应计算,表明了频域分析的优越性[10]。
基于上述研究成果,文章以有利于学生理解结构动力分析的基本方法和理论为目标,基于建筑结构抗震的实际教学算例[11],从时域和频率的角度,应用MatLab及其内部功能函数,探讨了该部分教学内容和数值模拟教学。
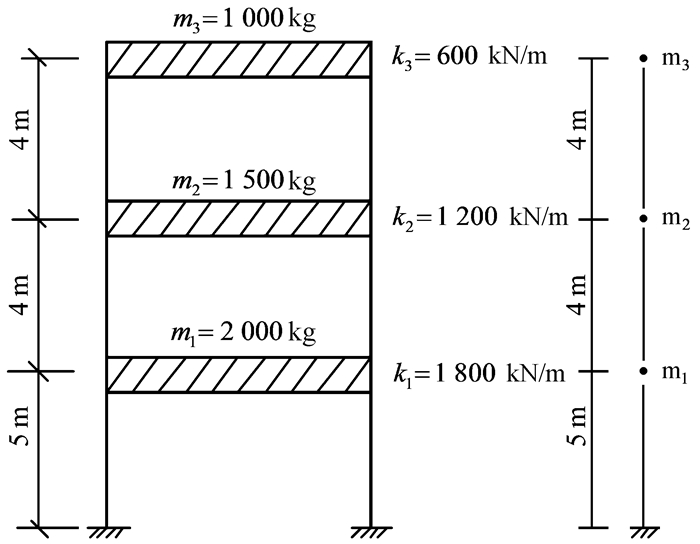
一、教学模型及其动力控制方程教学模型:三层剪切型结构,其基本参数如图 1所示[12]。在抗震设防烈度9度,多遇地震(加速度140 cm/s2)EL-Centro地震波作用下,计算该结构地震响应。
|
图 1 结构计算简图 |
该结构的动力控制微分方程为
| $ \left[ m \right]\left\{ {\ddot x} \right\} + \left[ c \right]\left\{ {\dot x} \right\} + \left[ k \right]\left\{ x \right\} = - \left[ m \right]\left\{ r \right\}{\ddot x_g} $ | (1) |
式中,{r}是影响系数,
| $ \begin{array}{l} \left[m \right] = \left[\begin{array}{l} 2\;\;\;\;0\;\;\;\;0\\ 0\;\;\;1.5\;\;\;0\\ 0\;\;\;\;0\;\;\;\;1 \end{array} \right] \times {10^3}, \\ \left[c \right] = \left[\begin{array}{l} 12.81\;\;\;\;-4.61\;\;\;\;\;0\\ -4.61\;\;\;\;7.88\;\;\;-2.31\\ \;\;\;\;0\;\;\;\;\;\; - 2.31\;\;\;2.95 \end{array} \right], \\ \left[k \right] = \left[\begin{array}{l} \;\;3\;\;\;\;-1.2\;\;\;\;\;0\\ -1.2\;\;\;\;1.8\;\;-0.6\\ \;\;0\;\;\;\; - 0.6\;\;\;\;0.6 \end{array} \right] \times {10^3}。 \end{array} $ |
该结构的状态方程为
| $ \left. \begin{align} & \dot{\tilde{x}}=A\tilde{x}+B\tilde{u} \\ & y=C\tilde{x}+D\tilde{u} \\ \end{align} \right\} $ | (2) |
式中,
| $ \begin{array}{l} B = \left[\begin{array}{l} \;\left\{ 0 \right\}\\ -\left\{ I \right\} \end{array} \right], \\ C = \left[\begin{array}{l} \left[I \right]\;\;\;\;\left[0 \right]\\ \left[0 \right]\;\;\;\;\left[I \right] \end{array} \right], \\ D = \left[\begin{array}{l} \left\{ 0 \right\}\\ \left\{ 0 \right\} \end{array} \right], \tilde x\left[\begin{array}{l} \left\{ x \right\}\\ \left\{ {\dot x} \right\} \end{array} \right], \\ \tilde u = \left[{{{\ddot x}_g}} \right], y = \tilde x。 \end{array} $ |
MatLab的内部函数,可以构建该结构的分析模型
| $ sys = ss\left( {A, B, C, D} \right) $ | (3) |
式中,ss(.)是MatLab内部函数。
其传递函数为
| $ H\left( s \right) = C{\left( {sI-A} \right)^{-1}}B + D $ | (4) |
利用内部函数ss2tf(.),应用状态方程计算传递函数为
| $ \left[{NUM, DEN} \right] = ss2tf\left( {A, B, C, D, iu} \right) $ | (5) |
式中,NUM=[b0 b1 … bm-1 bm]为传递函数分子,DEN=[a0 a1 … am-1 am]为传递函数分母。
此时,传递函数可以表示为
| $ H\left( \omega \right) = NUM\left( \omega \right)/DEN\left( \omega \right) $ | (6) |
应用MatLab可以简便地实现上述过程,见程序A。
M1=[2 000 0 0; 0 1 500 0; 0 0 1 000];
K1=[3 000 -1 200 0;-1 200 1 800 -600; 0 -600 600]*1e3;
C1=[12.814 -4.612 0;-4.612 7.881 -2.306; 0 -2.306 2.948]*1e3;
cn=size(M1, 1);%结构层数%
amax =1.4;%最大加速度峰值%
Eq=load(′el-centro.txt′); %输入地震加速度el-centro.txt波%
ffin=amax/max(abs(Eq))*Eq; %调整加速度峰值%
tmlg=size(Eq, 1);%地震加速度数量%
dt=0.02;%时间间隔%
tt=[0:1:(tmlg-1)]*dt; %加速度对应的时间%
I=eye(cn); O =zeros(cn); zz00=zeros(cn, 1); zz11=ones(cn, 1);
A=[O I; -M1\\K1-M1\\C1];B=[zz00;-zz11];C=eye(2*cn)′; D=[zz00;zz00];
sys = ss(A, B, C, D); %构建结构系统sys%
Hs =tf(sys); %结构系统传递函数Hs%
[NUM, DEN] =ss2tf(A, B, C, D, 1);%传递函数的分子、分母%
二、时域分析的单位脉冲响应和杜哈梅积分在t=0时,单位脉冲作用下,单自由度的结构响应函数h(t)为
| $ h\left( t \right) = {e^{ - \xi {\omega _n}t}}{\rm{sin}}{\omega _n}t/\left( {m{\omega _d}} \right) $ | (7) |
式中,
若t不等于0,而是t=τ,则冲击响应也将滞后时间τ。即有
| $ \begin{array}{l} h\left( {t-\tau } \right) = {e^{-\xi {\omega _n}\left( {t-\tau } \right)}}{\rm{sin}}{\omega _n}\left( {t - \tau } \right)/\left( {m{\omega _d}} \right)\\ \left( {t \ge \tau } \right) \end{array} $ | (8) |
应用线性叠加原理,则系统响应可以表示为
| $ x\left( t \right) = \int_0^t {h\left( {t-\tau } \right){{\ddot x}_g}\left( t \right)d\tau } $ | (9) |
式(9) 称为杜哈梅(Duhamel)积分式或卷积积分。
应用MatLab内部函数,卷积积分可以表示为
| $ {\rm{Di\_stm = conv}}\left( {{\rm{ffin, resp}}\left( {{\rm{:, ni}}} \right)} \right){\rm{*dt}} $ | (10) |
式中,conv(.)是卷积函数,dt是激励的时间间隔,ffin是激励的时间函数。
应用MatLab,可以实现结构的时域分析,见程序B。
[resp] =impulse(Hs, tt);
for ni =1:2*cn;
Di_stm=conv(ffin, resp(:, ni))*dt; Di_s3(:, ni)=Di_stm(1:tmlg);
end
运行结果见图 2,线型B。

|
图 2 结构位移时程响应 |
时域实函数f(t)的傅氏变换为
| $ F\left( \omega \right) = \int_{-\infty }^\infty {f\left( t \right){e^{-i\omega t}}dt} $ | (11.1) |
| $ f\left( t \right) = \frac{1}{{2\pi }} \int_{-\infty }^\infty {F\left( \omega \right){e^{i\omega t}}d} \omega $ | (11.2) |
式中,F(ω)称为函数f(t)的傅里叶正变换;f(t)也称为F(ω)的傅里叶逆变换。
MatLab提供了符号函数fourier和ifourier,分别对应傅里叶正变换和傅里叶逆变换。同时,也提供了数值计算方法,比如快速傅里叶变换fft(.)和快速傅里叶逆变换ifft(.)。为便于直接教学,采用直接编制程序的方法。
数值计算方法的傅里叶抽样点数必须满足2^nextpow2(tt),即NFFT =1024。如果地震输入个数不满足此条件,则在后面补上数值为0的值,使其满足抽样点数。同时,将式(11) 无穷域分别近似为[-TL2/2, TL2/2],TL2=NFFT×dt;逆变换域近似为[-8π, 8π]。为了满足对称性,将数据和时间进行平移,即平移TL2/2。
基于此,输入地震波的傅里叶正变换程序C为
NFFT =1024; %满足数值模拟的采样点个数
TL2=NFFT*dt; %计算时间域
tt2=linspace(-1/2, 1/2, NFFT)*TL2;%时间平移域
if (NFFT-tmlg)>0; for nmi=1:(NFFT-tmlg); ffin(tmlg+nmi)=0; end; end; %调整输入ffin个数
omgfw=16*pi; %频域范围近似为[-8π, 8π]
omg=linspace(-omgfw/2, omgfw/2, NFFT); %频域离散
Uomg4 =exp(-j*kron(omg, tt2′)′); %表示Kronecker积
Fomg21 =TL2/NFFT*Uomg4*ffin;%函数ffin的傅里叶正变换
地震波输入ffin的傅里叶变换为H(ω),则位移响应的傅里叶变换U(ω)为
| $ U\left( \omega \right) = H\left( \omega \right)F\left( \omega \right) $ | (12) |
此部分程序D为
[mmr, nnl]=size(NUM);
for mmi=1:mmr;
Trden4=0; Trnum4=0;
for nni=nnl:(-1):1
Trden4=Trden4+DEN(nnl+1-nni)*(i*omg).^(nni-1);
Trnum4=Trnum4+NUM(mmi, nnl+1-nni)*(i*omg).^(nni-1); end
ss1(:, mmi)=Trnum4./Trden4; %计算传递函数
Foutw(:, mmi)=Fomg21.*ss1(:, mmi); end; %计算位移响应傅里叶变换
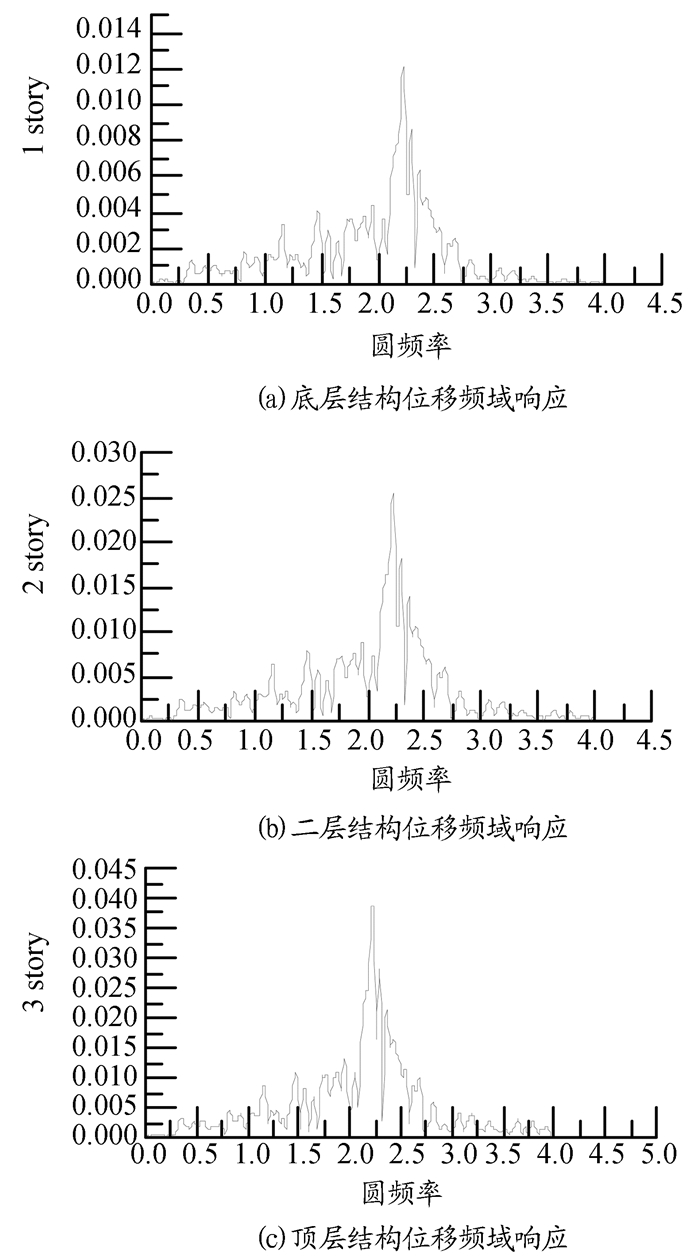
运行结果U(ω),即Foutw,计算结果见图 3。
|
图 3 结构位移频域响应 |
对位移响应的傅里叶变换U(ω)进行傅里叶逆变换,则结构的时域响应为
| $ {u_T}\left( t \right) = \frac{1}{{2\pi }}\int_{-\infty }^{ + \infty } {U\left( \omega \right){e^{i\omega t}}d\omega } $ | (13) |
由于将无穷域近似为有限频率,从计算的角度讲,结构的时域响应近似为
| $ {u_{{\omega _D}}}\left( t \right) = \frac{1}{{2\pi }}\int_{-{\omega _D}}^{ + {\omega _D}} {U\left( \omega \right){e^{i\omega t}}d\omega } $ | (14) |
式中,ωD=8π,本文频域范围近似取为[-8π, 8π]。
此部分程序E为
VF4=exp(j*kron(tt2′, omg)′);
for mmi=1:mmr
ytt(:, mmi) =omgfw/2/pi/NFFT*VF4′*Foutw(:, mmi);
for nmi=1:tmlg
ytt4(nmi, mmi)=real(ytt(NFFT-nmi+1, mmi));
end; end
位移响应运行结果见图 2的C线型。由于频率取值范围的影响,计算误差为
| $ {R_a} = {\rm{max}}\left| {{u_{{\omega _D}}}\left( t \right)} \right|{\rm{/max}}\left| {x\left( t \right)} \right| $ | (15) |
计算误差见表 1。
| 表 1 频域范围与计算误差 |
从表 1可以看出,如果频率取值过小,取得的结果与真实值相差较大。随着频率取值范围的扩大,计算精度逐渐提高,频率范围取值超过16π,计算精度可以满足实际需求。
五、结语文章从教学实例出发,给出了该结构时域卷积积分和杜哈梅积分,并通过傅里叶变换和传递函数,实现了结构的频域分析。通过建立时域与频域的转化关系,表明了时域和频域分析的优越性。通过参数变化分析,表明了参数变化对结构地震响应计算结果的影响。
通过MatLab强大的内部函数和简洁的编程平台,实现了结构时域和频域分析,为结构动力学的数值模拟提供了良好的平台和方法。通过MatLab的编程,可视化的仿真结果,有利于学生理解此部分教学内容,同时,增加学生对MatLab的学习兴趣。
| [1] | CloughR, PenzienJ. 结构动力学[M]. 2版. 高等教育出版社, 2006. |
| [2] | Rao S S. Mechanical Vibrations[M].Pearson Education Inc., 2011. |
| [3] | 陈清军, 李文婷. 结构动力学课程多元化教学方法探讨[J]. 高等建筑教育, 2015, 24(2): 47–52. DOI:10.11835/j.issn.1005-2909.2015.02.012 |
| [4] | 徐赵东. MATLAB语言在抗震工程中的应用[M]. 科学出版社, 2012. |
| [5] | 赖伟, 周至浩. MATLAB在结构地震动力分析中的应用[J]. 四川大学学报:工程科学版, 2000, 32(5): 14–18. |
| [6] | 黄晓吉. MATLAB在《结构动力学》课程教学中的应用[J]. 华东交通大学学报, 2006, 23(12): 55–56. |
| [7] | 李双艳, 刘长生, 谭跃辉, 王坤明. MATLAB在学习时域动力响应分析中的应用[J]. 教育教学论坛, 2012(5): 71–73. |
| [8] | 陈力宇, 高荣誉. 基于MATLAB混凝土框架结构动力弹性时程分析[J]. 安徽建筑工业学院学报:自然科学版, 2012, 20(1): 41–45. |
| [9] | 马乐为, 吴敏哲, 谢异同. 基于脉冲频响函数的MATLAB动力方程求解方法[J]. 世界地震工程, 2003, 19(2): 68–71. |
| [10] | 熊森, 周桂祥, 陈谋. 基于MATLAB和传递函数的结构动力响应计算[J]. 福建建筑, 2007(12): 34–36. |
| [11] | 李国强, 李杰, 陈素文, 等. 建筑结构抗震设计[M]. 中国建筑工业出版社, 2014. |
 2017, Vol. 26
2017, Vol. 26

