全国大学生结构设计竞赛是由教育部和中国土木工程学会联合主办,是教育部确定的大学生九项科技竞赛之一。从2005年浙江大学承办的第一届,到2016年天津大学承办的第十届,赛事日趋规范,为土木相关专业的大学生提供了锻炼综合素质,培养思维能力、动手能力、团队意识和专业素养的平台。随之而来,一些问题也随之显露,一部分参赛学生在刚拿到赛题时对结构设计的流程不清晰,为此,梳理总结竞赛结构设计流程,对发挥学科竞赛在土建类应用型人才培养中作用有着积极意义。
一、赛题简述第十届竞赛赛题为“大跨度空间结构”。赛题以中国大跨度结构最近三十年来取得的技术进步和广泛应用为背景,立足于结构设计极限状态(承载力极限状态和正常使用极限状态)基本概念,融入刚柔并济的结构设计理念,以激发大学生的创新能力为宗旨,使比赛更富有竞争性、不定性和观赏性。
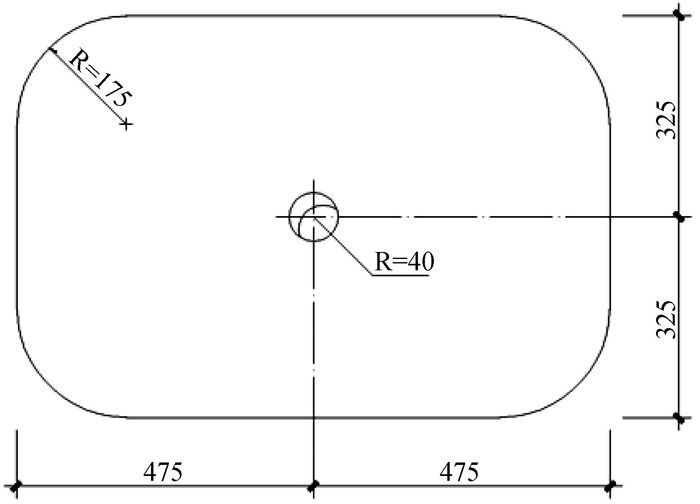
总体模型由给定的承台板、支承结构和屋盖结构三部分组成(图 1),支承结构和屋盖结构形式不限,但需满足使用空间的尺寸要求。模型制作需手工完成,材料为给定的竹材与502胶水。模型加载采用柔软的运动塑胶地板模拟屋面均布荷载。运动塑胶地板尺寸如图 2所示,并采用非接触式激光位移计测试屋面跨中挠度。模型加载前先铺屋面材料(重量1 kg),作为预加载,然后位移计读数清零。

|
图 1 模型三维透视示意简图 |
|
图 2 加载材料尺寸图 |
模型加载分为两个阶段,第一阶段(正常使用极限状态):标准加载14 kg(7张胶垫)。第一阶段中模型刚度得分Ki按以下方式计算模型刚度得分。
(a) 当wi≤[w]时,Ki=
(b) 当[w]<wi≤1.10[w]时,
Ki=
(c) 当wi>1.10[w]或wi<0时,Ki=0
此阶段,加载14 kg跨中挠度为4.00 mm时最佳。
第二阶段(承载力极限状态):最大加载, 此阶段的最大加载量由各参赛队根据自身模型情况自行确定。
给定竹材的力学指标如表 1所示。
| 表 1 竹材参考力学指标 |
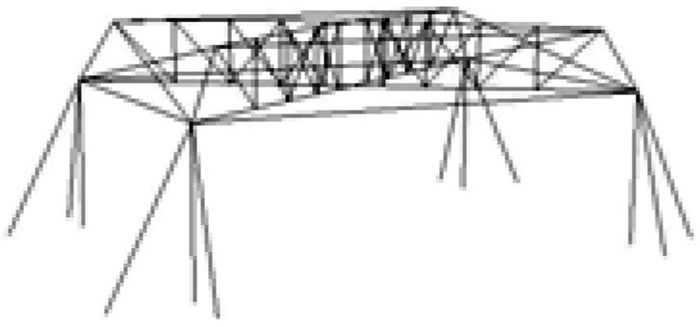
获特等奖作品(如图 3、图 4),结构屋盖部分主要由两榀梯形桁架交叉构成,结构上部横向联系采用拉条,在保证结构整体稳定性的同时,有效缩短了桁架上弦杆的杆长,单个立柱由一根压杆与两根拉条构成。整个结构重57.50 g,承重33 kg,第一阶段跨中挠度为3.56 mm。

|
图 3 交叉梯形桁架屋盖结构实物图 |
|
图 4 交叉梯形桁架屋盖结构简图 |
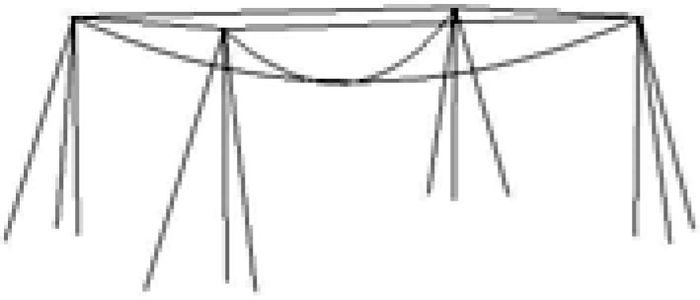
拉索式屋盖结构(图 5)由两根拉索交叉连接至四个立柱构成。该体系结构简单,受力时由两根拉索将加载垫的重力直接传递到立柱上,所以受力分析较为简单。赛题要求屋盖跨中第一阶段加载时的允许挠度[w]=4.00 mm,而拉索式结构的制作工艺、加载方式都对挠度有很大影响,稍有不慎就会超过4.00 mm,难以控制。
|
图 5 拉索式屋盖结构简图 |
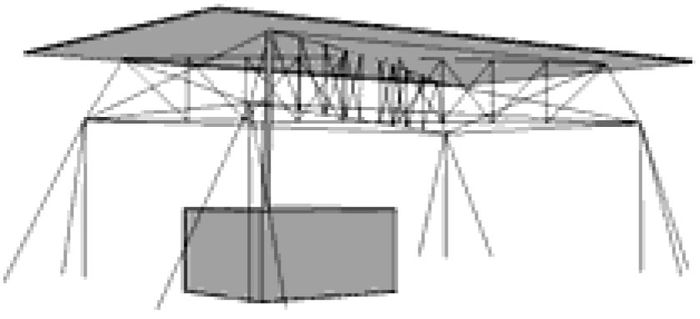
平行弦框架屋盖结构(图 6)由四榀桁架空间相互连接后再与四个立柱连接构成,该结构在受力上比交叉梯形桁架屋盖结构及拉索式屋盖结构稍为复杂,需要材料更多。在制作时四榀桁架节点更多,所以处理难度更大。

|
图 6 平行弦框架屋盖结构简图 |
对比三种结构,拉索式屋盖结构最为简洁,制作最为方便,但挠度难以控制。对比理论设计及实验发现,交叉梯形桁架屋盖结构比平行弦框架屋盖结构轻15 g左右,而交叉梯形桁架屋盖结构制作也较为简便,所以选择交叉梯形桁架屋盖结构进一步优化设计。
三、结构优化 (一) 荷载分布优化加载时,在结构上部放置柔软的运动塑胶地板,以达到施加荷载的目的。结合运动地板的软硬程度及模型结构特点,注意到模型在承载时载荷并非均布面荷载。由于材料特性,软垫在中部会略微拱起而使部分运动地板与结构接触不紧密,而靠近结构边缘的运动地板则会略微下垂。考虑采用如图 7所示的“顶推”荷载试验法确定桁架各节点所受荷载的大小。在结构上方加载15 kg,结构下方放置电子秤,用一根长度合适的杆件将加载垫稍微顶起,记录电子秤上的读数,然后依次测量各个点,最后进行数据处理,直到得出节点荷载分布的规律(如图 8)。
|
图 7 “顶推”荷载试验示意图 |

|
图 8 节点载荷分布比例图 |
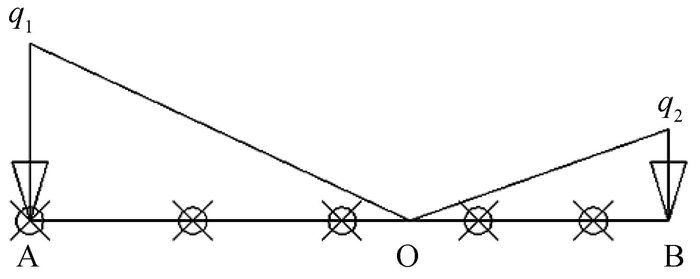
由图 8可知,结构所承受载荷是不均匀的,从A点到B点,荷载分布比例先减小,后增大,所以可将屋盖结构上的荷载简化为线性分布荷载。屋盖结构承受的荷载具有对称性,取AB段对简化荷载作说明,则可将AB段的荷载简化为图 9所示的线性分布荷载,经测量AO段长l1=0.28 m,BO段长l2=0.19 m。
|
图 9 荷载分布示意图 |
假设屋盖结构上方承重1N,取AO段,
q1=1.46N/m
取BO段
q2=0.47N/m
故第一阶段模型上承受的载荷为15 kg时,
q1′=215.25N/m
q2′=69.63N/m
第二阶段,模型上承受的载荷为设计极限承载力40 kg时,
q1′′=574.00N/m
q2′′=185.68N/m
(二) 截面形状优化分析屋盖结构采用两榀桁架交叉,再用横向联系连成整体,因此,把模型分析简化为平面应力问题,即只研究一榀桁架,施加的运动地板加载荷载取一半,在横向支撑足够的情况下,做以上假设是合理的。
单榀桁架为对称结构,故其左半部分结构简图如图 10所示,桁架截面尺寸如表 2所示。

|
图 10 单榀桁架结构简图 |
| 表 2 桁架杆件截面尺寸 |
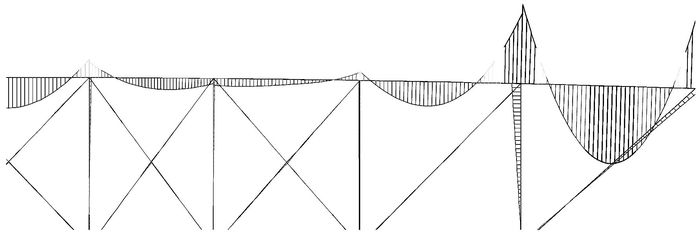
加载时结构上弦杆与运动地板直接接触,所以上弦杆所受的力主要为轴力和弯矩。采用MIDAS有限元分析软件计算出承载力极限状态下上弦杆的弯矩图(图 11),桁架所受弯矩具有对称性,图 11为上弦杆的一半。
|
图 11 上弦杆弯矩图 |
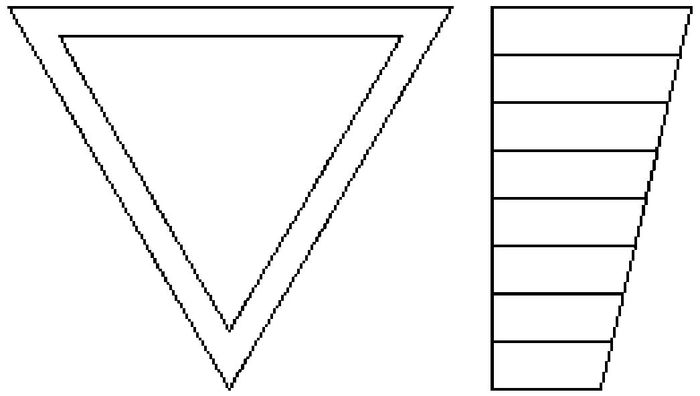
在弯矩和轴力共同作用下,上弦杆沿截面所受轴向力近似分布规律如图 12所示。
|
图 12 上弦杆轴向应力近似分布规律 |
将截面轴向力分布与实际制作过程相结合,最终选定了符合力学规律又方便制作的三角形空心截面杆作为上弦杆。
上弦杆b以外的其他压杆的工作状态方向性可忽略不计,所以设计成两个正交方向一致的截面更合理。例如,可以采用正四边形箱形截面,因为正四边形截面在两个正交方向的惯性均相等,此时,
| ${I_1} = \frac{1}{2} \times 2t \times {a^3} + ta \times {a^2} = \frac{7}{6}t{a^3}$ | (1) |
截面面积为,
| ${S_1} = 4at$ | (2) |
在相同厚度下,空心圆截面惯性矩为,
| ${I_2} = \frac{\pi }{8}t{d^3}$ | (3) |
横截面积为,
| ${S_2} = \pi dt$ | (4) |
两者的截面惯性矩之比为
| $\frac{{{I_1}}}{{{I_2}}} = \frac{{\frac{7}{6}t{a^3}}}{{\frac{\pi }{8}t{d^3}}} = \frac{{28}}{{3\pi }}\frac{{{a^3}}}{{{d^3}}}$ | (5) |
为了在相同的横截面积下进行比较,令(2)和(4)相等,解得
| $\frac{a}{d} = \frac{\pi }{4}$ | (6) |
带入(5)得
| $\frac{{{I_1}}}{{{I_2}}} = 1.4393$ | (7) |
所以,在等厚度和等面积的条件下,箱形比空心圆的惯性矩大44%。这里使用等厚度条件是为了两种界面的局部失稳应力相近,空心圆截面由于有壳的效应,实际局部稳定临界应力要大一些。当半径较大时,上述误差不大。
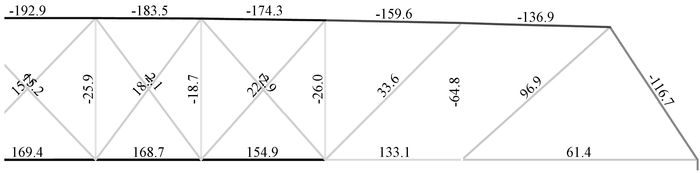
通过MIDAS得出承载力极限状态下桁架轴力图,由图 13可知,桁架内所有斜杆均按照受拉设计,故斜杆截面为较细实腹形矩形截面,可受拉而不可受压。
|
图 13 桁架轴力图 |
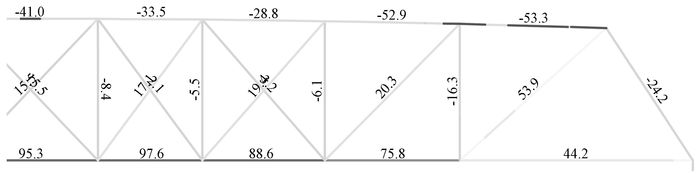
经MIDAS分析,承载力极限状态下桁架各杆件组合应力(图 13),其中最大拉应力σ1=95.3MPa<[σ1]=150 MPa,最大压应力σ2=53.3MPa<[σ2]=65 MPa,故截面设计满足强度要求。
(三) 横向联系优化分析空间两榀桁架容易发生平面外失稳,故要对桁架施加横向联系。横向联系的设计方案主要有两种。
第一种方案全部采用拉条对桁架节点进行约束(图 14)。图中细实线为对桁架进行约束的拉条,每个桁架节点在横向两个方向上都有拉条加以约束,所以桁架的每个节点都被约束了,桁架的稳定性也能得到保证,虚线部分用来连接桁架与立柱,加强了桁架与立柱间的连接,提高了桁架与立柱间的整体性和稳定性。
|
图 14 桁架组合应力图 |
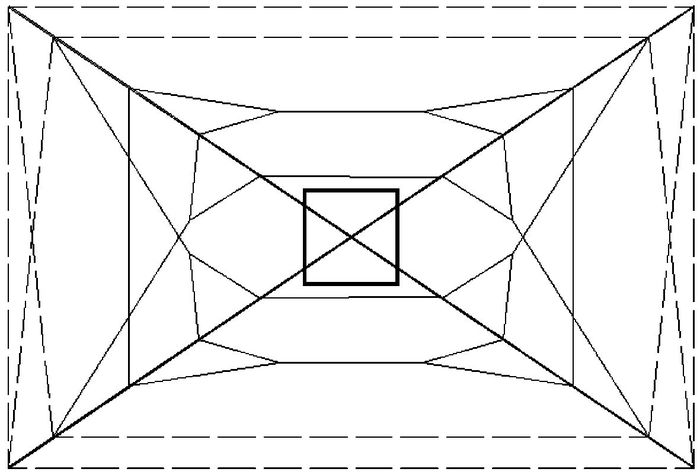
第二种方案采用拉条、压杆组合的方式对桁架节点进行约束(图 15)。图中细实线为可受拉、可受压的杆件,按图示细实线方案排布杆件即可约束桁架两个方向的失稳,虚线部分则为拉条,同样用来连接桁架与立柱,保证了结构的整体性和稳定性。
|
图 15 拉条约束 |
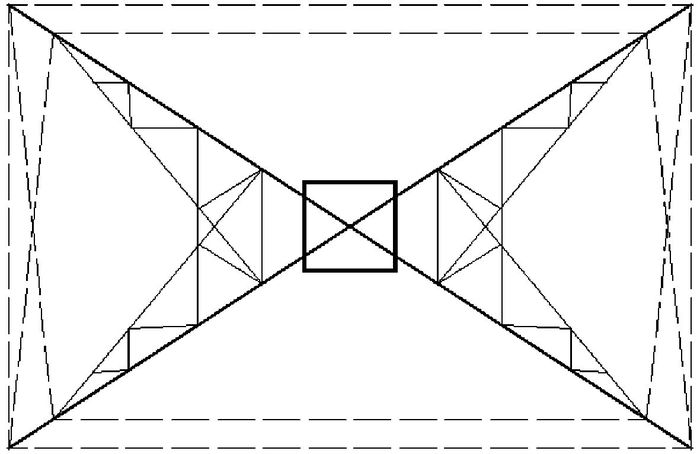
对比实验结果,两种方案的效果没有明显差别。但在重量上,第一种和第二种分别为6g和14g。故采用了第一种方案。
|
图 16 拉条、压杆组合约束 |
由桁架轴力图(图 13)可知,桁架上弦杆各段轴力并不相同,所以上弦杆需要调整。对上弦杆进行调整时可采用等间距、不等截面的方法进行调整,也可采用等截面、不等间距的方法进行调整。
采用等间距、不等截面的调整方法对截面进行调整,可使上弦杆每一段的应力大小相差不大,使材料强度得到充分利用,但是这种调整方法,在制作时比较困难。
结构中的杆件可以看成是细长杆,所以杆件在达到强度极限前就已正失稳破坏,所以,采用等截面、不等间距的方法。此外,该调整操作也更为简便。根据实际情况调整,可得单榀桁架结构简图(图 10)中标注的杆长分布。
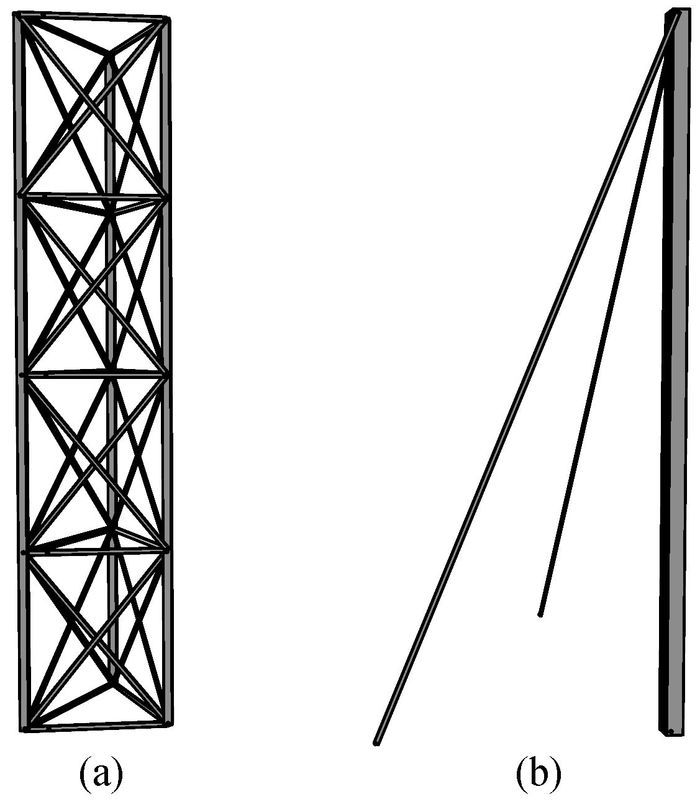
(五) 立柱优化分析立柱的设计方案主要有以下两种(如图 17)。
|
图 17 立柱两种方案结构简图 |
第一种方案(图 17a),每根立柱由三根长为300 mm的竖直杆,这种结构做立柱比较稳定,但是立柱结构复杂、受力不明确,从而无法使模型上部重量均匀的分布在每个立柱杆上,从而材料无法得到充分利用,且制作复杂、重量比第二种方案更重,故舍弃。
第二种方案(图 17b)结构较为简洁,较粗的一根杆件用来承受模型传给的竖向压力,另外两根拉条则用来保证立柱和整体模型的稳定性。四个立柱之间桁架的横向联系拉条沿边框连接,立柱和上部形成一个稳定的结构,最终采用此方案。
(六) 结构整体优化分析将两榀桁架直接交叉组合后进行受力分析,得到w=5.13 mm。
将两榀桁架直接交叉组合,再围上四根边框拉条,进行受力分析,得到正常使用极限状态下跨中挠度w=3.72 mm。
由桁架轴力图 13及上述受力分析可知:
(1) 将两榀桁架直接进行组合后,桁架中各杆的轴力均有减小。
(2) 将两榀桁架组合后,再围上四根边框拉条,桁架中各杆件的轴力相对于没有围上边框拉条之前有所减小。
(3) 相对于没有围上边框拉条,围上边框拉条后跨中挠度从5.13 mm变成了3.72 mm。
边框拉条使跨中挠度、结构尺寸满足要求的同时,还维持了结构的稳定性,保证了结构的整体性。
围上边框拉条的实际结构在正常使用极限状态下跨中挠度为3.56 mm,与计算值w=3.72 mm相比误差较小,证明了理论分析与选型的正确性。
在加载时,运动地板的横向移动将通过连接桁架间的拉条传递给立柱上端,每个立柱由两根拉条维持了其稳定性,四个立柱相互连接在一起,因此结构可有效抵抗加载时的横向干扰。
加载过程中,上弦杆受力逐渐变大,上弦杆在发生横向弯曲时,连接上弦杆的横向联系将限制上弦杆节点的位移,从而有效缩短了上弦杆的杆长,从而使其承受的力变大,整个模型的承载能力也将随之增大。
四、结语大学生结构设计竞赛是一个综合性较强的竞赛,主要考察参赛队伍各个方面的能力。在设计一个结构模型时, 首先应该考察一个模型的体系,选择一个合理的结构进行分析,然后根据所加载荷进行研究。弄明白了载荷分布后,结合MIDAS等有限元分析软件对结构进行受力分析,根据受力分析的结果,对截面进行调整。最后根据实际情况对结构的整体稳定性进行优化。一个优秀的结构模型作品不仅考察学生对专业知识和技能的掌握,还对学生的创新能力、发现和解决问题的能力,以及团队合作和吃苦精神提出更高要求。
| [1] | 沈璐, 高潮, 王志云. 第七届全国大学生结构设计竞赛模型结构设计与分析[J]. 高等建筑教育, 2014, 23(4): 159–163. DOI:10.11835/j.issn.1005-2909.2014.04.037 |
| [2] | 李学罡, 蔡明兮. 材料力学[M]. 吉林: 吉林科学技术出版社, 2005. |
| [3] | 周克明. 结构的优化设计分析——大学生结构设计竞赛评述[J]. 福建建筑, 2006(4): 28–30. |
| [4] | 张炎胜, 陆新征. 大学生结构设计大赛中的计算机仿真分析[J]. 力学与实, 2009(31): 110–112. |
 2017, Vol. 26
2017, Vol. 26