2. 河南大学 数学与统计学院, 河南 开封 475004
2. School of Mathematics and Statistics, Henan University, Kaifeng 475004, P. R. China
“卓越工程师教育培养计划”是中国高等院校工程教育改革的重大举措,是促进高等院校专业人才培养适应社会和经济发展的一项质量工程[1]。
力学课程包含有理论力学、材料力学、结构力学等,其作为高等院校工科专业如水利工程、土木工程和机械工程等必修的专业基础课程,在基础课和专业课之间起着承前启后的重要作用。力学课程既有较强的理论性,又与工程实践紧密联系,具有很强的实用性。力学课程的学习有助于培养学生科学的思维方式和分析解决工程实际问题的能力,满足学生日后从事专业研究和项目开发等工作的要求。因此,力学课程教学是卓越工程师教育培养计划不可缺少的重要环节。
力学课程涉及高等数学众多知识。高等数学为专业课程提供必需的数学概念、理论、方法和运算技能。在力学课程教学过程中应引导学生将所学的高等数学知识应用到力学课程学习中,一方面帮助学生巩固高等数学知识,提高学生应用数学知识的能力;另一方面激发学生的学习兴趣,培养学生科学创新思维能力,使力学课程教学真正收到实效,起到承前启后的作用[2]。
基础课程与专业课程的交叉和渗透越来越受到学者的广泛关注。如依据高等数学中的导数、微分概念绘制材料力学中梁的剪力和弯矩等内力图[3],以二重积分计算力学中构件的截面惯性距[3],应用高斯定律推导流体力学中流体的连续性方程[4],用Dirac函数统一表述力学中的集中力、集中力偶矩以及瞬时脉冲力等物理量[5],应用三角函数实现力学中坐标系转换等[3, 6]。高等数学中常常将函数展开为三角级数形式,本文通过引入Fourier三角级数,求解材料力学两端简支梁受集中力作用和结构力学中两端固定梁受均布荷载作用的静定问题,以及一端固定一端简支且带中间铰的梁受均布荷载作用的超静定问题,探讨Fourier三角级数在力学课程教学中的应用。
一、Fourier三角级数基本知识 (一) Fourier三角级数由基本三角函数系组成的三角级数
| $ \frac{{{a_0}}}{2} + \sum\limits_{n = 1}^\infty {({a_n}{\rm{cos}}nx + {b_n}{\rm{sin}}nx)} $ | (1) |
若三角级数式(1)中各项系数an、bn由在[-π, π]上定义且绝对可积的函数f(x)按下式得到,即
| $ \left\{ \begin{array}{l} {a_n} = \frac{1}{\pi }\int_{-\pi }^\pi {f\left( x \right){\rm{cos}}nxdx\;\;n = 0, 1, 2, \cdots \cdots } \\ {b_n} = \frac{1}{\pi }\int_{-\pi }^\pi {f\left( x \right)\mathit{sin}nxdx\;\;n = 1, 2, 3, \cdots \cdots } \end{array} \right. $ | (2) |
则称式(1)为f(x)的Fourier三角级数,简称Fourier级数;an、bn为Fourier系数。
f(x)满足Dirichlet收敛定理时,f(x)的Fourier级数展开式为
| $ f\left( x \right) = \frac{{{a_0}}}{2} + \sum\limits_{n = 1}^\infty {({\mathit{a}_n}{\rm{cos}}{\mathit{n}_x} + {b_n}{\rm{sin}}{\mathit{n}_x})} $ | (3) |
对于周期为2l的绝对可积函数f(x)满足Dirichlet收敛定理时,f(x)的Fourier级数展开式为
| $ f\left( x \right) = \frac{{{a_0}}}{2} + \sum\limits_{n = 1}^{{a_0}} {({\mathit{a}_n}{\rm{cos}}\frac{{n\pi x}}{l} + {b_n}{\rm{sin}}\frac{{n\pi x}}{l})} $ | (4) |
其中,
| $ \left\{ \begin{array}{l} {a_n} = \frac{1}{l}\int_{-l}^l {f(x)\mathit{cos}\frac{{n\pi x}}{l}dx\;\;\;\;n = 0, 1, } 2, \cdots \cdots \\ {b_n} = \frac{1}{l}\int_{ - l}^l {f(x)sin\frac{{n\pi x}}{l}dx\;\;\;\;n = 1,2,3, \cdots \cdots } \end{array} \right. $ | (5) |
当f(x)为奇函数时,Fourier系数an、bn表达式式(2)、式(5)变化为
| $ \left\{ \begin{array}{l} \;\;\;\;\;\;\;\;{a_n} = 0\\ {b_n} = \frac{2}{\pi }\int_0^\pi {f\left( x \right)sinnxdx\;n = 1, 2, 3, \cdots \cdots } \end{array} \right. $ |
| $ \left\{ \begin{array}{l} \;\;\;\;\;\;\;\;{a_n} = 0\\ {b_n} = \frac{2}{l}\int_0^l {f\left( x \right)sin\frac{{n\pi x}}{l}dx\;\;\;n = 1, 2, 3, \cdots \cdots } \end{array} \right. $ |
则f(x)的Fourier级数展开式为
| $ f(x) = \sum\limits_{n = 1}^\infty {{b_n}\sin \mathit{nx}} $ | (6) |
称为f(x)的Fourier正弦级数,简称正弦级数。
当f(x)为偶函数时,Fourier系数an、bn表达式式(2)、式(5)变化为
| $ \left\{ \begin{array}{l} {a_n} = \frac{2}{\pi }\int_0^\pi {f\left( x \right){\rm{cos}}nxdx\;n = 0, 1, 2, \cdots \cdots } \\ \;\;\;\;\;\;\;\;{b_n} = 0 \end{array} \right. $ |
| $ \left\{ \begin{array}{l} {a_n} = \frac{2}{l}\int_0^l {f\left( x \right)cos\frac{{n\pi x}}{l}dx\;n = 0, 1, 2, \cdots \cdots } \\ \;\;\;\;\;\;\;\;{b_n} = 0 \end{array} \right. $ |
则f(x)的Fourier级数展开式为
| $ f(x) = \frac{{{a_0}}}{2} + \sum\limits_{n = 1}^\infty {{a_n}\cos {n_x}} $ | (7) |
称为f(x)的Fourier余弦级数,简称余弦级数。
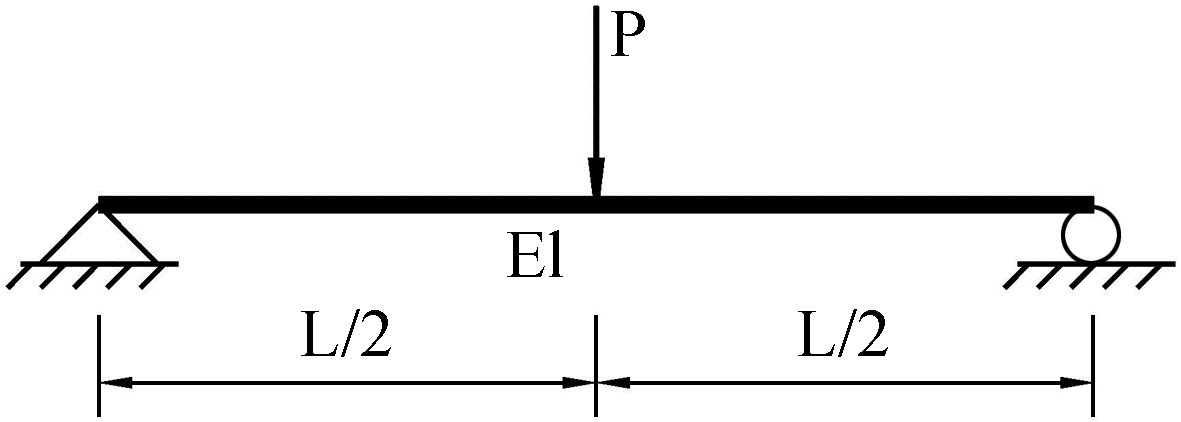
二、Fourier三角级数的应用 (一) 在材料力学课程教学中的应用图 1所示为等截面两端简支的梁,梁跨度为l,抗弯刚度为EI,梁跨中受集中力P作用,求跨中的挠度。
|
图 1 集中力作用的简支梁 |
以梁左端支座为原点,建立x坐标轴,其正方向水平向右。因梁两端简支,可知
| $ {w_0} = {w_l} = 0\;\;{M_0} = {M_l} = 0 $ | (8) |
根据边界条件(8),设梁的挠度函数w(x)为正弦级数,即
| $ w(x) = \sum\limits_{n = 1}^\infty {{w_n}\sin \frac{{n\pi x}}{l}} $ | (9) |
对梁的挠度函数w(x)对x进行四次求导得
| $ {w^{({\rm{I}}V)}}(x) = \sum\limits_{n = 1}^\infty {{w_n}\frac{{{n^4}{\pi ^4}}}{{{l^4}}}\sin \frac{{n\pi x}}{l}} $ | (10) |
根据Dirac函数的性质[5],将集中荷载P展成正弦级数,即
| $ \begin{array}{*{20}{l}} {q = P\delta (x - \frac{l}{2}) = \frac{{2P}}{l}\sum\limits_{n = 1}^\infty {sin\frac{{n\pi }}{2}} \sin \frac{{n\pi x}}{l} = }\\ {\frac{{2P}}{l}\sum\limits_{n = 1,3, \cdots \cdots }^\infty {( - 1)\frac{{n - 1}}{2}\sin \frac{{n\pi x}}{l}} } \end{array} $ | (11) |
将式(10)、式(11)代入梁的平衡微分方程
EIw(ΙV)(x)=q
得到
| $ \left\{ {\begin{array}{*{20}{l}} {{w_n} = \frac{{\frac{{\left( { - 1} \right)n - 1}}{2} \cdot 2p{l^3}}}{{{n^4}{\pi ^4}EI}}\;\;\;\;\;\;n = 1,3, \cdots \cdots }\\ {\;\;\;\;\;\;{w_n} = 0\;\;\;\;\;\;\;\;\;\;\;\;\;n = 2,4, \cdots \cdots \;} \end{array}} \right. $ |
将其代入式(10),并令x=l/2,得到
| $ w(\frac{l}{2}) = \frac{{2P{l^3}}}{{{\pi ^4}EI}}\sum\limits_{n = 1, 3, \cdots }^\infty {\frac{1}{{{n^4}}} = \frac{{P{l^3}}}{{48EI}}} $ |
在本科材料力学课程教学中,对于上述静定问题的求解步骤为:首先根据梁的受力情况,得到梁的弯矩函数,然后建立挠度曲线与弯矩之间关系的微分方程,对其进行x的二次积分后得到梁的挠度曲线函数,最后求得具体位置的挠度值。而在本文求解中,先假定梁的挠度曲线函数为包含待定系数的Fourier正弦级数的形式, 使其全部满足或部分满足边界条件, 由Dirac函数将集中力同样转换为正弦级数形式,根据梁的受力平衡方程求出挠度曲线函数中的待定系数, 求得具体位置的挠度值,从而省去了求弯矩方程的过程。
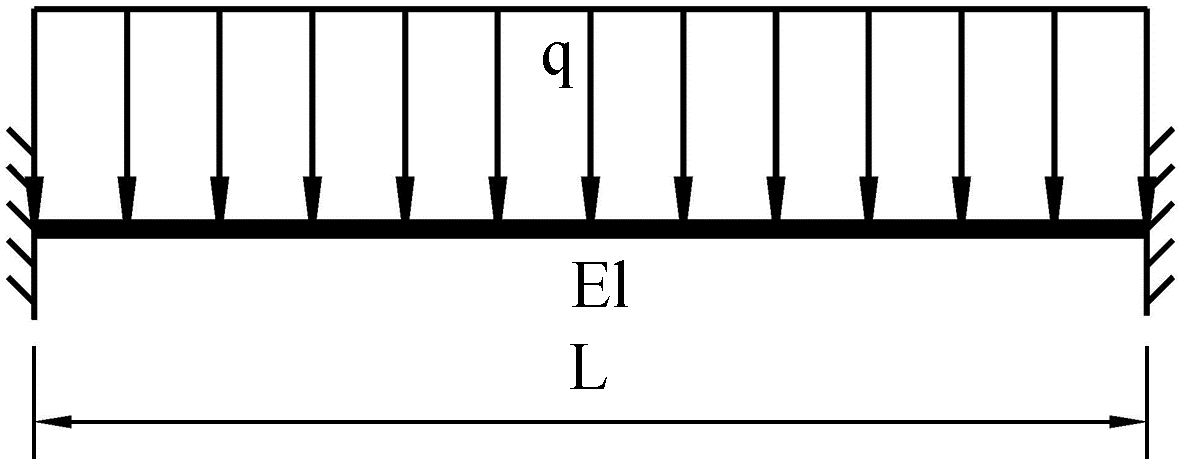
(二) 在结构力学课程教学中的应用图 2为等截面两端固定的梁,梁跨度为l,抗弯刚度为EI,受均布荷载q作用,求跨中的挠度和两端的弯矩。
|
图 2 均布荷载作用的固定梁 |
以梁左端支座为原点,建立x坐标轴,其正方向水平向右。因梁两端固定,可知
| $ {\theta _0} = {\theta _l} = 0\;\;\;{Q_0} = \frac{{ql}}{2}, {Q_l} =-\frac{{ql}}{2} $ | (12) |
根据边界条件(12),设梁的挠度函数w(x)为带多项式的余弦级数,即
| $ w\left( x \right) = \frac{{{w_0}}}{2} + \sum\limits_{n = 1}^\infty {{w_n}} {\rm{cos}}\frac{{n\pi x}}{l} + \frac{q}{{24EI}}{x^2}{(\mathit{l-x})^2} $ | (13) |
对梁的挠度函数w(x)对x进行四次求导得
| $ {w^{({\rm I}V)}}\left( x \right) = \sum\limits_{n = 1}^\infty {{w_n}\frac{{{n^4}{\pi ^4}}}{{{l^4}}}\cos \frac{{n\pi x}}{l} + \frac{q}{{EI}}} $ | (14) |
将式(14)代入梁的平衡微分方程
EIw(ΙV)(x)=q
得到wn=0
则梁的挠度函数式(13)变化为
| $ w(x) = \frac{{{w_0}}}{2} + \frac{q}{{24EI}}{x^2}{(\mathit{l-x})^2} $ | (15) |
由边界条件可知:w0=0,将其代入式(15),得到
| $ w(\mathit{x}) = \frac{q}{{24EI}}{x^2}{(\mathit{l-x})^2} $ | (16) |
梁中点x=l/2处的挠度为
| $ w(\frac{l}{2}) = \frac{{q{l^4}}}{{384EI}} $ |
对式(16)对x进行二次求导,进而得到梁的弯矩
| $ M(\mathit{x}) =-\mathit{EIw''}{\rm{(}}\mathit{x}{\rm{) =-}}\frac{q}{{12}}({\mathit{l}^2}-6\mathit{lx {\rm{ + }} }{\rm{6}}{\mathit{x}^2}) $ | (17) |
端点x=0, x=l处的弯矩为
M0=Ml=-ql2/12
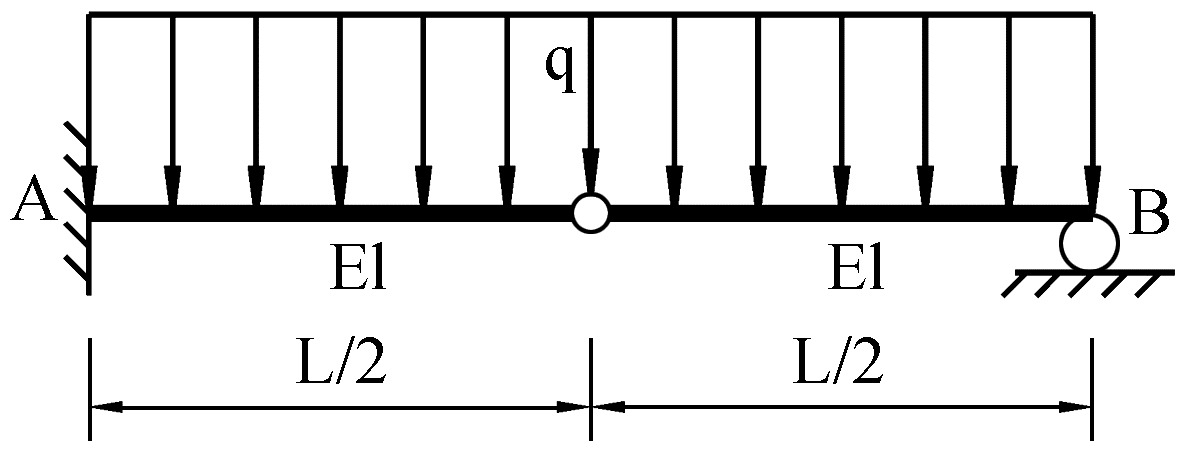
图 3为等截面一端固定一端简支梁,梁跨中采用铰接,受均布荷载q作用,求梁左端弯矩和中间铰两侧相对转角。
|
图 3 跨中铰接的梁 |
以梁左端支座为原点,建立x坐标轴,其正方向水平向右。将梁等效为两端简支,梁除受均布荷载q作用外,梁左端A处有力偶MA作用。中间铰左右转角差值设为ΔθC。
等效后梁为两端简支,设梁的挠度函数为正弦级数,即
| $ w(\mathit{x}) = \sum\limits_{n = 1}^\infty {{w_n}\sin \frac{{n\pi x}}{l}} $ | (18) |
等效后,作用于梁的荷载为
| $ q(x) = q - {M_A}\delta '(\mathit{x}{\rm{ - 0}}) + \mathit{EI\Delta }{\theta _c}\delta ''(x - l{\rm{/2}}) $ | (19) |
将荷载展为正弦级数,即
| $ q(x) = \sum\limits_{n = 1}^\infty {{q_n}\sin \frac{{n\pi x}}{l}} $ | (20) |
其中,
| $ \left\{ {\begin{array}{*{20}{l}} {{q_n} = \frac{{2n\pi {M_A}}}{{{l^2}}} + \frac{{4q}}{{n\pi }} - ( - 1)\frac{{n - 1}}{2}\frac{{2{n^2}{\pi ^2}}}{{{l^3}}}EI\mathit{\Delta }{\theta _C}}\\ {\;\;\;\;\;n = 1,3,5, \cdots \cdots }\\ {{q_n} = \frac{{2n\pi }}{{{l^2}}}{M_A}}\\ {\;\;\;\;\;n = 2,4,6, \cdots \cdots } \end{array}} \right. $ |
对式(18)求四次导数得
| $ {w^{({\rm I}V)}}(x) = \sum\limits_{n = 1}^\infty {{w_n}\frac{{{n^4}{\pi ^4}}}{{{l^4}}}\sin \frac{{n\pi x}}{l}} $ | (21) |
将式(20)、式(21)代入微分方程
EIw(ΙV)(x)=q
得到
| $ \left\{ \begin{array}{l} {w_n} = \frac{{2{l^2}{M_A}}}{{{n^3}{\pi ^3}EI}} + \frac{{4q{l^4}}}{{{n^5}{\pi ^5}EI}}-(-1)\frac{{n-1}}{2}\frac{{2\mathit{\Delta }{\theta _C}l}}{{{n^2}{\pi ^2}}}\\ \;\;\;\;\;\;\;n = 1, 3, 5, \cdots \cdots \\ {w_n} = \frac{{2{l^2}{M_A}}}{{{n^3}{\pi ^3}EI}}\\ \;\;\;\;\;\;\;n = 2, 4, 6, \cdots \cdots \end{array} \right. $ |
则梁的挠度函数为
| $ \begin{array}{l} w(x) = \sum\limits_{n = 1}^\infty {\frac{{2{l^2}{M_A}}}{{{n^3}{\pi ^3}EI}}\sin \frac{{n\pi x}}{l} + \sum\limits_{n = 1, 3, \cdots \cdots }^\infty {[\frac{{4q{l^4}}}{{{n^5}{\pi ^5}EI}}} }- \\ (-1)\frac{{n-1}}{2}\frac{{2\mathit{\Delta }{\theta _C}l}}{{{n^2}{\pi ^2}}}]\sin \frac{{n\pi x}}{l} \end{array} $ | (22) |
对式(22)求导,并根据边界条件w'(0)=0得到
| $ \Delta {\theta _C} = \frac{{2{M_A}l}}{{3EI}} + \frac{{q{l^3}}}{{12EI}} $ | (23) |
对式(22)求二次导数,得到
| $ \begin{array}{l} M(x) =- \mathit{EIw''}{\rm{(}}\mathit{x}{\rm{) = }}\sum\limits_{n = 1}^\infty {\frac{{2{M_A}}}{{n\pi }}\sin \;\frac{{n\pi x}}{l}} + \\ \sum\limits_{n = 1, 3, \cdots \cdots }^\infty {[\frac{{4q{l^2}}}{{{n^3}{\pi ^3}}}-(-1)\frac{{n-1}}{2}\frac{{2EI\mathit{\Delta }{\theta _C}}}{l}]{\rm{sin}}\frac{{n\pi x}}{l}} \end{array} $ | (24) |
当x=l/2时,由原来的M(
| $ 为M(\frac{l}{2}) =-\mathit{EI\Delta }{\theta _C}\delta (\mathit{x-l}{\rm{/2}}) $ | (25) |
且
| $ \begin{array}{l} \delta (\mathit{x-}\frac{l}{2}) = \frac{2}{l}\sum\limits_{n = 1}^\infty {\mathit{sin}\frac{{n\pi }}{2} = \frac{2}{l}\sum\limits_{n = 1, 3, \cdots \cdots }^\infty {} } \\ (-1)\frac{{n-1}}{2}\sin \frac{{n\pi x}}{l} \end{array} $ | (26) |
联立式(24)、式(25)和式(26)得到
MA=-ql2/4
将其代入式(23)得到
| $ \mathit{\Delta }{\theta _C} =-\frac{{q{l^3}}}{{12EI}} $ |
在结构力学课程的教学中,对于上述两个超静定问题的求解过程为:首先采用力法或位移法求出梁的弯矩函数,然后根据单位荷载法求解相应的值。而本文的求解过程则如上所述。
可见,引入Fourier三角级数求解力学问题的核心思想,为构造全部满足或部分满足边界条件的包含待定系数的奇或偶调,以及Fourier三角级数构件变形函数,由构件的平衡方程求出变形函数中的待定系数, 从而求出构件的变形、转角和弯矩。
三、结语在力学课程教学中,引入Fourier三角级数,通过求解材料力学两端简支梁受集中力作用和结构力学中两端固定梁受均布荷载作用的静定问题,以及一端固定一端简支且带中间铰的梁受均布荷载作用的超静定问题,表明Fourier三角级数在力学课程教学中的可行性和适用性。将Fourier三角级数引入力学课程教学中,可以加深学生对数学与力学知识的理解,促进基础知识与专业课程内容的融合及渗透,引导和培养学生开放而多元化的思维,锻炼学生综合应用所学知识解决实际问题的能力,有助于卓越工程师教育培养计划创新型人才的培养。
| [1] | 林健. 卓越工程师创新能力的培养[J]. 高等工程教育研究, 2012(5): 1–17. |
| [2] | 程敏. 高等数学在工程力学中的具体应用[J]. 鄂州大学学报, 2012, 19(5): 71–73. |
| [3] | 沈玉凤, 许英姿, 刘露. 材料力学教学中加强高等数学知识的运用, 培养学生科学思维能力[J]. 大学教育, 2013(12): 58–59. DOI:10.3969/j.issn.2095-3437.2013.12.025 |
| [4] | 刘今子, 邸伟娇, 宋国亮, 等. 结合"渗流力学"实现"高等数学"案例式教学[J]. 科教文汇, 2015(10): 50–51. DOI:10.3969/j.issn.1672-7894.2015.10.023 |
| [5] | 雷进生, 刘章军. Dirac函数在力学教学中的应用[J]. 高等建筑教育, 2014, 23(3): 85–88. DOI:10.11835/j.issn.1005-2909.2014.03.022 |
| [6] | 刘章军, 雷进生. 弹性力学教学中数学与力学问题的美学探讨[J]. 高等建筑教育, 2015, 24(1): 59–63. DOI:10.11835/j.issn.1005-2909.2015.01.015 |
 2018, Vol. 27
2018, Vol. 27

