学生成绩是学生学习情况和教师教学效果的重要体现,也是促进教学改革、加强教学管理和提高教学质量的重要依据。然而高校学生成绩评定受到很多因素的制约,很难得到一个确切的评价结果。因此,研究一种合理公平的学生成绩评定方法非常必要。
模糊数学法是应用模糊数学的有关理论,对多因素的制约关系进行数学化的抽象归纳,建立一个反映其本质特征和动态过程的理想化评价模式[1]。模糊数学综合评判方法适用于评价因素多、结构层次多的对象系统[2]。笔者尝试采用模糊综合评判方法对学生一门课程的成绩进行综合评价。实践证明:该方法可以提高学生成绩评价的合理性和准确性。
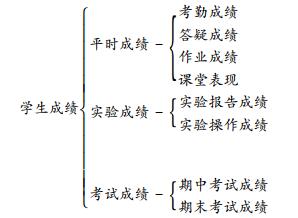
二、模糊综合评判的数学模型 (一) 问题描述学生成绩的影响因素主要包括考勤成绩、答疑成绩、作业成绩、实验成绩、期中期末考试成绩。此外, 学生的成绩还与课堂表现、学习认真程度等因素有关,其中许多因素的评价都依赖于成绩评价者的主观感受,带有很强的主观性。成绩评价的等级,例如通用的五级评价标准:优、良、中、及格、不及格,两两之间并没有一个明确的界限, 属于模糊性事件。因此, 学生成绩评定具有模糊性, 是一种模糊的随机变量,应用模糊数学理论进行学生成绩评定是较科学合理的。影响高校学生成绩的因素见图 1。
|
图 1 影响高校学生成绩的主要因素 |
在实际工作中,对一个事物的评价, 常常涉及多个因素或多个指标,这就要求根据多个因素对事物作出综合评价,而不能只从某一因素的情况去评价事物,这就是综合评判[3]。但是并非所有的综合评判问题都可以用模糊数学的方法来解决,若用模糊数学理论综合分析评判问题需要具备三个特征,称为模糊评判的三个基本要素[4],即评判客体在概念上具有模糊性,评判主体在思维方法上具有多样性,评判结果在表达上具有口语化特征。很明显, 对学生成绩的评定具有上述三个特征,可以用模糊数学理论对其进行综合评判。
根据以上描述,由于评价因素较多,结构层次为二级,因此对学生成绩的评定宜采用二级综合评判模型。
(三) 模糊综合评判模型及运算(1) 将因素集U分为3组:U1={u1, u2, u3, u4}, U2={u5, u6}, U3={u7, u8}.其中U1为平时成绩,U2为实验成绩,U3为考试成绩,u1,u2, u3,u4, u5,u6, u7,u8分别为考勤成绩、答疑成绩、作业成绩、课堂表现、实验报告成绩、实验操作成绩、期中测试成绩和期末考试成绩。
(2) 设评判集V={v1, v2, v3, v4, v5}。v1为优,v2为良,v3为中,v4为及格,v5为不及格。其中90分及以上为优,80~89分为良,70~79分为中,60~69分为合格,60分以下为不合格。
(3) 对每个Ui(i=1, 2, 3)中的因素进行单因素评判,有U1={u1, u2, u3, u4}, 取权重为A1=(0.2, 0.2, 0.3, 0.3),U2={u5, u6}, 取权重为A2=(0.6, 0.4),U3={u7, u8}, 取权重为A3=(0.3, 0.7)。
建立评判矩阵,由5名评价人员组成评定小组,对某个学生的考试成绩、实验成绩、平时成绩三个因素进行评定,并分设5个等级,即优、良、中、合格和不合格,要求评定人员客观进行评价。全部评价结束后,收集评定人员的评定表,再进行统计分析。学生成绩评价统计见表 1。
| 表 1 学生成绩评价统计表 |
令
| $ {R_1} = \left( {\begin{array}{*{20}{c}} {0.8}&{0.2}&0&0 \\ {0.6}&{0.2}&{0.2}&0 \\ {0.4}&{0.4}&0&{0.2} \\ {0.4}&0&{0.4}&{0.2} \end{array}\;\;\;\;\begin{array}{*{20}{c}} 0 \\ 0 \\ 0 \\ 0 \end{array}} \right) $ |
| $ {R_2} = \left( {\begin{array}{*{20}{c}} {0.8}&0 \\ {0.2}&{0.4} \end{array}\;\;\;\;\begin{array}{*{20}{c}} 0&{0.2} \\ 0&{0.4} \end{array}\;\;\;\;\begin{array}{*{20}{c}} 0 \\ 0 \end{array}} \right) $ |
| $ {R_3} = \left( {\begin{array}{*{20}{c}} 0&{0.4} \\ 0&{0.2} \end{array}\;\;\;\;\begin{array}{*{20}{c}} {0.4}&{0.2} \\ {0.4}&{0.4} \end{array}\;\;\;\;\begin{array}{*{20}{c}} 0 \\ 0 \end{array}} \right) $ |
对二级因素作单级模糊综合评判,取主观因素决定型模型M(∧,∨)计算,可得:
| $ \begin{gathered} {B_1} = {A_1} \circ {R_1} \hfill \\ = \left( {0.2, 0.2, 0.3, 0.3} \right) \circ \left( {\begin{array}{*{20}{c}} {0.8}&{0.2}&0&0 \\ {0.6}&{0.2}&{0.2}&0 \\ {0.4}&{0.4}&0&{0.2} \\ {0.4}&0&{0.4}&{0.2} \end{array}\;\;\;\;\begin{array}{*{20}{c}} 0 \\ 0 \\ 0 \\ 0 \end{array}} \right) \hfill \\ = \left( {0.3, 0.3, 0.3, 0.2, 0.0} \right) \hfill \\ \end{gathered} $ |
| $ \begin{gathered} {B_2} = {A_2} \circ {R_2} \hfill \\ = \left( {0.6, 0.4} \right) \circ \left( {\begin{array}{*{20}{c}} {0.8}&0 \\ {0.2}&{0.4} \end{array}\;\;\;\;\begin{array}{*{20}{c}} 0&{0.2} \\ 0&{0.4} \end{array}\;\;\;\begin{array}{*{20}{c}} 0 \\ 0 \end{array}} \right) \hfill \\ = \left( {0.6, 0.4, 0.0, 0.4, 0.0} \right) \hfill \\ \end{gathered} $ |
| $ \begin{gathered} {B_3} = {A_3} \circ {R_3} \hfill \\ = \left( {0.3, 0.7} \right) \circ \left( {\begin{array}{*{20}{c}} 0&{0.4} \\ 0&{0.2} \end{array}\;\;\;\begin{array}{*{20}{c}} {0.4}&{0.2} \\ {0.4}&{0.4} \end{array}\;\;\;\begin{array}{*{20}{c}} 0 \\ 0 \end{array}} \right) \hfill \\ {\rm{ = }}\left( {0.0, 0.3, 0.4, 0.4, 0.0} \right) \hfill \\ \end{gathered} $ |
(4) 对第一级因素U={U1, U2, U3}, 设权重为A=(0.2, 0.1, 0.7)
令总单因素评判矩阵为
| $ R = \left( \begin{gathered} {B_1} \hfill \\ {B_2} \hfill \\ {B_3} \hfill \\ \end{gathered} \right) = \left( {\begin{array}{*{20}{c}} {0.3}&{0.3}&{0.3} \\ {0.6}&{0.4}&{0.0} \\ {0.0}&{0.3}&{0.4} \end{array}\;\;\;\begin{array}{*{20}{c}} {0.2} \\ {0.4} \\ {0.4} \end{array}\;\;\;\begin{array}{*{20}{c}} {0.0} \\ {0.0} \\ {0.0} \end{array}} \right) $ |
作二级模糊综合评判,可得:
| $ \begin{gathered} B = A \circ R \hfill \\ = \left( {0.2, 0.1, 0.7} \right) \circ \left( {\begin{array}{*{20}{c}} {0.3}&{0.3}&{0.3} \\ {0.6}&{0.4}&{0.0} \\ {0.0}&{0.3}&{0.4} \end{array}\;\;\;\begin{array}{*{20}{c}} {0.2} \\ {0.4} \\ {0.4} \end{array}\;\;\;\begin{array}{*{20}{c}} {0.0} \\ {0.0} \\ {0.0} \end{array}} \right) \hfill \\ = \left( {0.2, 0.3, 0.4, 0.4, 0.0} \right) \hfill \\ \end{gathered} $ |
归一化得:
| $ \begin{gathered} B' = \left( {\frac{{0.2}}{{1.3}}, \frac{{0.3}}{{1.3}}, \frac{{0.4}}{{1.3}}, \frac{{0.4}}{{1.3}}, \frac{{0.0}}{{1.3}}} \right) \hfill \\ = \left( {0.15, 0.23, 0.31, 0.31, 0.00} \right) \hfill \\ \end{gathered} $ |
可知,结果无法分辨出学生成绩的评定等级,因此选用加权平均模型M(∧,+)再次计算,公式如下:
| $ {b_j} = \sum\limits_{i = 1}^5 {{a_i}{r_{ij}}} \left( {j = 1, 2, 3, 4, 5} \right) $ |
对二级因素进行单级综合评判,可得:
| $ \begin{gathered} {B_1} = {A_1} \circ {R_1} \hfill \\ = \left( {0.2, 0.2, 0.3, 0.3} \right) \circ \left( {\begin{array}{*{20}{c}} {0.8}&{0.2}&0&0 \\ {0.6}&{0.2}&{0.2}&0 \\ {0.4}&{0.4}&0&{0.2} \\ {0.4}&0&{0.4}&{0.2} \end{array}\;\;\;\begin{array}{*{20}{c}} 0 \\ 0 \\ 0 \\ 0 \end{array}} \right) \hfill \\ = \left( {0.52, 0.2, 0.16, 0.12, 0.0} \right) \hfill \\ \end{gathered} $ |
| $ \begin{gathered} {B_2} = {A_2} \circ {R_2} \hfill \\ = \left( {0.6, 0.4} \right) \circ \left( {\begin{array}{*{20}{c}} {0.8}&0 \\ {0.2}&{0.4} \end{array}\;\;\;\begin{array}{*{20}{c}} 0&{0.2} \\ 0&{0.4} \end{array}\;\;\;\begin{array}{*{20}{c}} 0 \\ 0 \end{array}} \right) \hfill \\ = \left( {0.56, 0.16, 0.0, 0.28, 0.0} \right) \hfill \\ \end{gathered} $ |
| $ \begin{gathered} {B_3} = {A_3} \circ {R_3} \hfill \\ = \left( {0.3, 0.7} \right) \circ \left( {\begin{array}{*{20}{c}} 0&{0.4} \\ 0&{0.2} \end{array}\;\;\;\begin{array}{*{20}{c}} {0.4}&{0.2} \\ {0.4}&{0.4} \end{array}\;\;\;\begin{array}{*{20}{c}} 0 \\ 0 \end{array}} \right) \hfill \\ = \left( {0.0, 0.26, 0.4, 0.34, 0.0} \right) \hfill \\ \end{gathered} $ |
| $ R = \left( \begin{gathered} {B_1} \hfill \\ {B_2} \hfill \\ {B_3} \hfill \\ \end{gathered} \right) = \left( {\begin{array}{*{20}{c}} {0.52}&{0.2}&{0.16} \\ {0.56}&{0.16}&{0.0} \\ {0.0}&{0.26}&{0.4} \end{array}\;\;\;\begin{array}{*{20}{c}} {0.12} \\ {0.28} \\ {0.34} \end{array}\;\;\;\begin{array}{*{20}{c}} {0.0} \\ {0.0} \\ {0.0} \end{array}} \right) $ |
| $ \begin{gathered} B = A \circ R \hfill \\ = \left( {0.2, 0.1, 0.7} \right) \circ \left( {\begin{array}{*{20}{c}} {0.52}&{0.2}&{0.16} \\ {0.56}&{0.16}&{0.0} \\ {0.0}&{0.26}&{0.4} \end{array}\;\;\;\begin{array}{*{20}{c}} {0.12} \\ {0.28} \\ {0.34} \end{array}\;\;\;\begin{array}{*{20}{c}} {0.0} \\ {0.0} \\ {0.0} \end{array}} \right) \hfill \\ = \left( {0.16, 0.238, 0.312, 0.29, 0.0} \right) \hfill \\ \end{gathered} $ |
按最大隶属度原则,该学生的成绩应为中等。
三、结语本文对建立适用于学生成绩评定的二级模糊综合评判模型进行了探讨。先采用主观因素决定模型M(∧,∨)进行模糊运算,导致无法判别学生成绩的等级,之后改用加权平均模型M(∧,+),得出学生成绩的综合评定级别为中等。结果显示:加权平均综合评判模型能考虑所有的影响因素,充分体现综合评判的作用,可以较为客观、公正地反映学生对所学专业课程的掌握情况和实践能力,为提高学生成绩评价的准确性提供理论依据。
| [1] | 魏永义, 赵永敢, 王飞. 模糊数学法在学生成绩评价中的应用[J]. 卫生职业教育, 2011(8): 40–41. |
| [2] | 谢季坚, 刘承平. 模糊数学方法及其应用[M]. 4版. 武汉: 华中科技大学出版社, 2013. |
| [3] | 宗宏. 高校教室热环境模糊综合评判及数值模拟[D]. 哈尔滨: 哈尔冰工业大学, 2008. |
| [4] | 刘运通, 胡江碧. 模糊评判的数学模型及其参数估计[J]. 北京工业大学学报, 2001, 27(1): 112–115. |
 2018, Vol. 27
2018, Vol. 27


