工程结构所用的材料是可变形的,因此结构在荷载作用下会发生变形,而这种变形会引起结构各位置的变化,即结构的位移。对于初学者而言,定量地画出结构内力图比较容易,但是定性或定量地绘制超静定结构或者复杂结构在荷载作用下的变形图却难以掌握。
在国内结构力学教材[1-2]中, 单位荷载法是求解超静定结构位移的一般方法,该方法简单快速,但是利用此方法绘制结构变形图有一定难度。在国外教材[3-5]中, 面积矩法是一种求解梁挠度的方法,它的概念清晰,但其几何关系不直观,在解题时经常在各种几何关系上花掉大量的时间。面积矩法适用广泛,也被很多学者用于前沿问题的研究,例如在最近的研究中用来计算高层建筑伸臂系统[6]或者复杂三明治板[7]的位移。本文提出了快速面积矩法,该方法不仅可以定量求解结构在简单荷载下的位移和挠度,还可以定量和定性地绘制结构变形图,使得面积矩法的几何关系更加清晰直观,同时加强学生对于结构变形组成的理解能力及快速绘制结构变形图的能力。
一、面积矩法的介绍一简支梁在荷载作用下变形,在梁上取一微段dx,如图 1所示,变形后左右截形成的夹角为dθ,M为弯矩,EI为抗弯刚度。

|
图 1 微段示意图 |
曲线的曲率半径为ρ,则
| $ {\rm{d}}\theta = \frac{{{\rm{d}}x}}{\rho } $ | (1) |
又有关系
| $ \frac{1}{\rho } = \frac{M}{{EI}} $ | (2) |
联立方程(1)和(2)得到
| $ {\rm{d}}\theta = \frac{M}{{EI}}{\rm{d}}x $ | (3) |
在AB区间内对上式进行积分,可以得到A、B两点的转角差θBA
| $ \theta _{_B}^{^A} = \smallint _{_B}^{^A}\frac{M}{{EI}}{\rm{d}}x $ | (4) |
其几何意义为A、B间曲率图
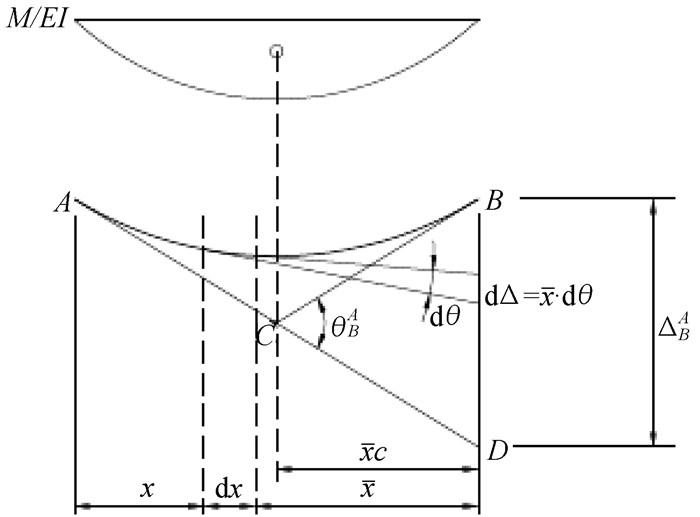
如图 2所示,以dx微段为研究对象,可知在梁末端铅垂线上的偏差为:
|
图 2 变形曲率关系图 |
| $ d\mathit{\Delta } = \bar x\cdot{\rm{d}}\theta = \bar x\cdot\frac{M}{{EI}}{\rm{d}}x $ | (5) |
其中x为dx区段内曲率图面积形心到B点的距离。
对上式在AB区间内积分,同时利用(4)式可得
| $ \mathit{\Delta }_{_B}^{^A} = \smallint _{_A}^{^B}\bar x\cdot\frac{M}{{EI}}{\rm{d}}x = \smallint _{_A}^{^B}{\bar x_{\rm{c}}}\cdot\frac{M}{{EI}}{\rm{d}}x $ | (6) |
其中
在此应该明确一点:梁挠曲线上两点切线的交点和这两点间曲率图的形心在一条铅垂线上。要证明这一点并不难,推算如下。
如图 2中所示,
我们可以在寻找挠度和角度的几何关系时利用这一点从而加快求解结构位移和挠度以及快速绘制结构变形图。
二、快速面积矩法的提出面积矩法概念清晰,但是想要直接快速地绘制结构变形图还有一定难度,故基于面积矩法的基本原理,我们提出了快速面积矩法。主要的做法就是在区段曲率图面积形心处加上一个弹簧铰,将梁看作刚性,在荷载作用下变形至与变形曲线相切,即可快速画出结构变形图,然后找出相应的几何关系用面积矩法即可求解位移和挠度。该方法的基本思想是用刚性体——弹簧体系中转动弹簧的转动变形来等效代替变形体的变形,“快速”体现在变形几何关系的确定简单快速。
现利用例题1介绍快速面积矩法绘制结构变形图和求解目标点挠度的三个步骤。
例1:如图 3所示一截面抗弯刚度为EI的等直简支梁,求C点的挠度大小。

|
图 3 计算简图 |
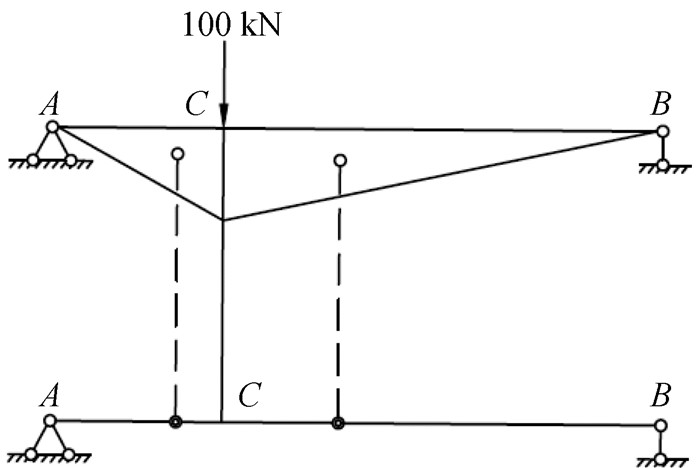
(1) 作出梁的曲率图,以所求点为分界将曲率图分为两部分,在曲率图上找出两区段的形心,在形心位置处加上弹簧铰(图示用两个同心圆表示弹簧铰以区分弹簧铰和理想铰)如图 4。
|
图 4 添加弹簧铰将梁分段 |
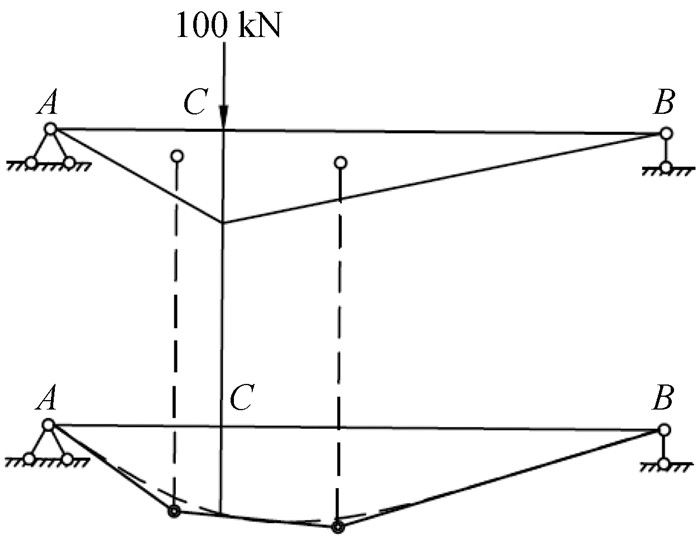
(2) 分段的梁作为刚性体系,在荷载作用下,使弹簧铰交点沿铅垂线变形,绘制出与各个折线段相切的光滑的曲线即为结构的变形图,如图 5。
|
图 5 弹簧铰法绘制变形图 |
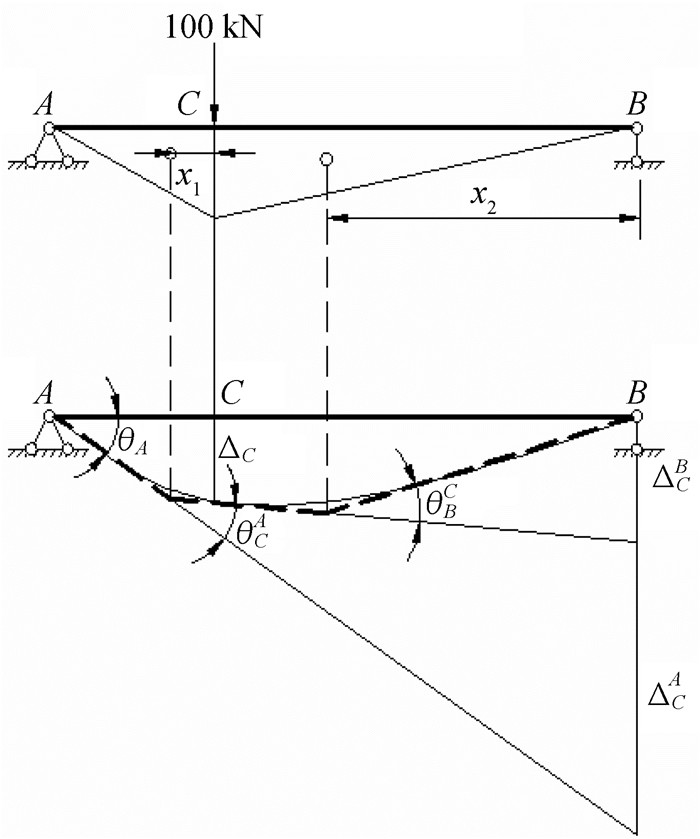
(3) 根据结构变形图找出几何关系并利用面积矩法公式求解挠度如图 6。
|
图 6 曲率变形关系图 |
从图 6中可以清楚地看出如下几何关系:
| $ \begin{array}{l} {\mathit{\Delta }_C} = {\theta _A}\cdot{l_{AC}} - \theta _{_C}^{^A}\cdot{x_1}\\ {\theta _A} = \frac{{\mathit{\Delta }_{_B}^{^A}}}{{{l_{AB}}}} = \frac{{\mathit{\Delta }_{_C}^{^A} + \mathit{\Delta }_{_B}^{^C}}}{{{l_{AB}}}}\\ \mathit{\Delta }_{_C}^{^A} = \theta _{_C}^{^A}\cdot\left( {{x_1} + {l_{CB}}} \right)\\ \mathit{\Delta }_{_B}^{^C} = \theta _{_B}^{^C}\cdot{x_2} \end{array} $ |
其中x1=1/3为左边三角形形心到C点的水平距离,x2=2为右边三角形形心到B点的水平距离,θCA和θBC则可根据曲率面积求出:
从上例可以看出,利用快速面积矩法方法可以快速地绘制结构变形图,从而根据几何关系用面积矩法快速地求解挠度,不仅对简单荷载下的悬臂梁和简支梁可以用此方法,对于复杂荷载下的外伸梁也是可以利用叠加法和逐段钢化的方法简化为简单荷载的悬臂梁和简支梁来求解。但是这种方法也存在一个问题:如果所求点两边曲率图不是规则的图形,那么求解它们的形心位置将带来一定的困难。其实这也是可以利用叠加法来解决的,此处不再详细说明。
快速面积矩法利用刚体加弹簧体的变形等效代替变形体的变形,用刚体转动体系代替变形体系,让求解速度大大加快,使求解过程几何关系直观,以直代曲的概念清晰,不仅可以定量求解结构中关键点的位移和转角,还可以定量画出结构变形图,降低了同学们掌握结构变形图的难度。
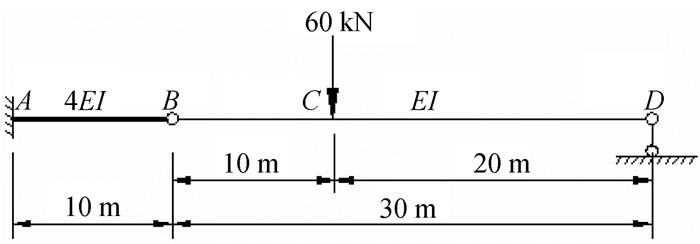
三、快速面积矩法与单位荷载法的对比例2:分别用快速面积矩法和单位荷载法求图 7结构中C点的位移和转角。
|
图 7 计算简图 |
解答:(1)用快速面积矩法求解:
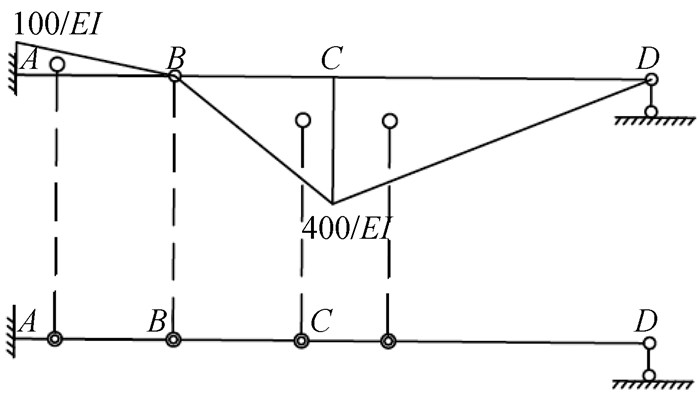
作出梁的曲率图,以所求点和铰接点为分界将曲率图分为三部分,在曲率图上找出三区段的形心,在形心位置处加上弹簧铰如图 8。
|
图 8 添加弹簧铰将梁分段 |
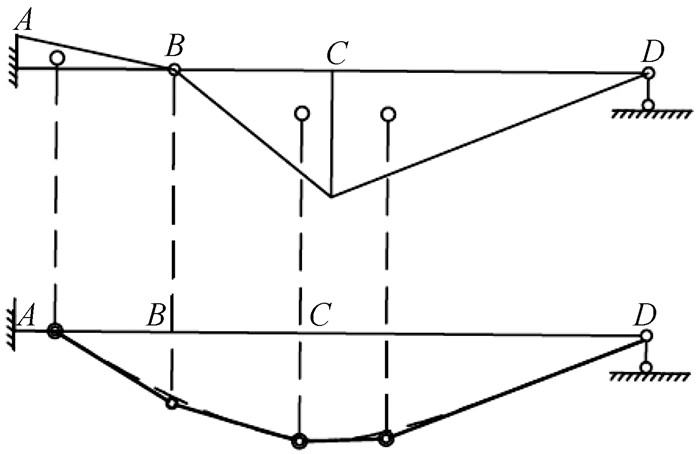
分段的梁作为刚性体系,在荷载作用下,使弹簧铰交点沿铅垂线变形,绘制出与各个折线段相切的光滑的曲线即为结构的变形图如图 9。
|
图 9 弹簧铰法绘制变形图 |
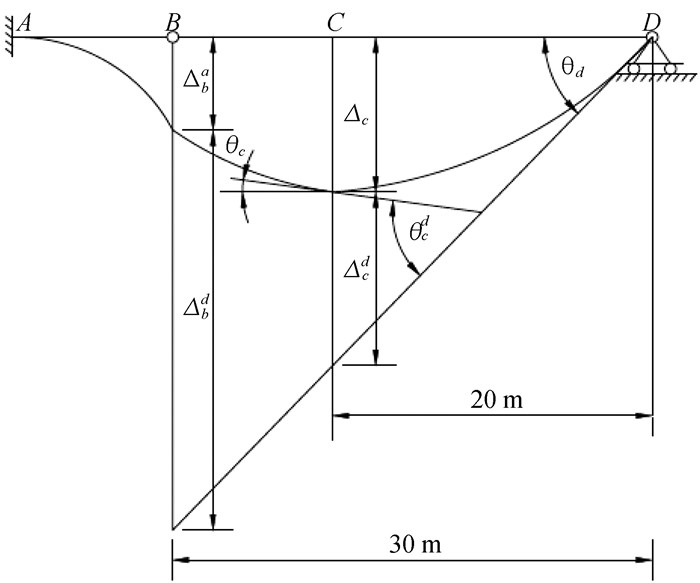
根据结构变形图找出几何关系并利用面积矩法公式求解挠度如图 10。
|
图 10 曲率变形关系图 |
分析结构变形图可知,若要求C点的转角,可先利用上文面积矩法所述公式(6)求得
| $ \begin{array}{l} \mathit{\Delta }_{_B}^{^A} = \frac{{10000}}{{3EI}}\\ \mathit{\Delta }_{_D}^{^B} = \frac{{240000}}{{3EI}} \end{array} $ |
从而根据几何关系
| $ {\theta _D} = \frac{{\mathit{\Delta }_{_B}^{^A} + \mathit{\Delta }_{_D}^{^B}}}{{{l_{BD}}}} = \frac{{25000}}{{9EI}} $ |
再利用上文所述公式(4)求得
| $ \theta _{_C}^{^D} = \frac{{4000}}{{EI}} $ |
故求出c的转角为
| $ {\theta _C} = \theta _{_C}^{^D} - {\theta _D} = \frac{{11000}}{{9EI}} $ |
利用公式(6)求得
| $ \begin{array}{l} \mathit{\Delta }_{_C}^{^D} = \frac{{80000}}{{3EI}}\\ {\mathit{\Delta }_C} = {\theta _D}\cdot{l_{CD}} - \mathit{\Delta }_{_C}^{^D} = \frac{{260000}}{{9EI}} \end{array} $ |
(2) 用单位荷载法求解:
画出结构的荷载弯矩图MD如图 11所示和单位弯矩M1和M2图分别如图 12和图 13所示。
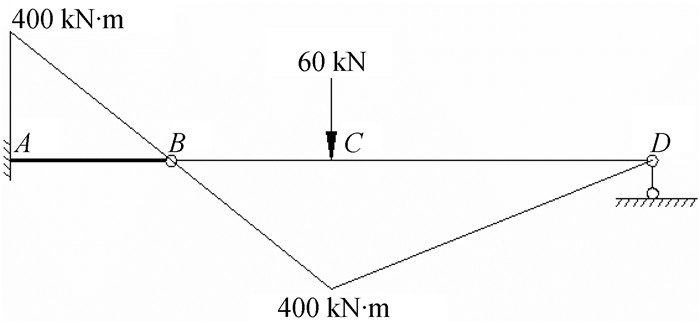
|
图 11 荷载弯矩图 |
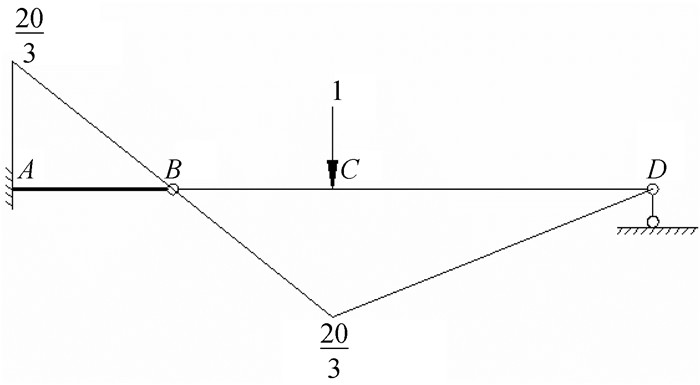
|
图 12 单位弯矩M1图 |
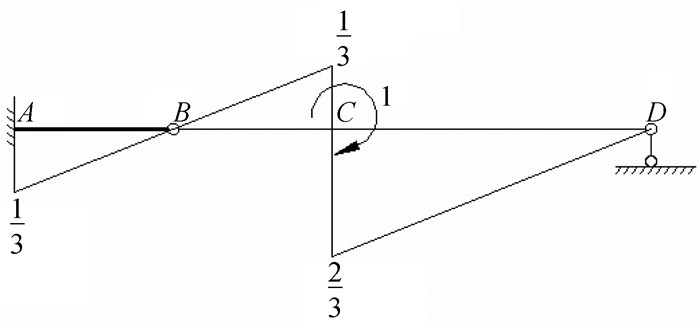
|
图 13 荷载弯矩M2图 |
由图乘法可知;MD和M1图乘求得:
| $ {\mathit{\Delta }_C} = \frac{{260000}}{{9EI}} $ |
MD和M2图乘求得:
| $ {\theta _C} = \frac{{11000}}{{9EI}} $ |
从此例对比快速面积矩法和单位荷载法可以看出,一方面快速面积矩法几何关系直观、概念清楚,求解结构关键点处的位移ΔDC、ΔDB、ΔCD和挠度θD、θCD的同时,就能够快速绘制出结构变形图,降低了学生绘制结构变形图的难度,并且使学生对于结构变形的组成部分理解得更加透彻和深入。利用一个结构变形图,就可以方便求得关键点的位移ΔC和转角θC。
另一方面,单位荷载法计算简单方便,可以用来校核快速面积矩法以保证求解的正确性,但是对于比较复杂的结构,单位荷载法计算量大,需要多图绘制,纯粹变成数学求解问题。用单位荷载法求结构位移的正负号和挠度的方向往往也是学生比较容易混淆的部分,即使计算结果正确也有可能绘制出来的结构变形图不正确,对于初学结构力学的学生而言,单位荷载法不能提高学生快速绘制结构变形图的能力。
四、结语本文提出的快速面积矩法不仅可以定量求解结构关键点在简单荷载下的位移和转角,还可以定量和定性地绘制结构变形图,使得面积矩法的几何关系更清晰直观,加强学生对于结构变形组成的理解能力及快速绘制结构变形图的能力。
单位荷载法计算简单方便,但是结构位移的正负号和挠度的方向往往是学生比较容易混淆的部分,即使计算结果正确也有可能绘制出来的结构变形图不正确。另一方面,由于快速面积矩法结构位移和变形的几何关系紧密联系,求解需要逐步递推,如果其中一个未知量求解错误则会导致最终结果出错,因此单位荷载法作为一种有效的手段用来校核快速面积矩法以保证求解的正确性。
| [1] | 朱慈勉. 结构力学:上, 下[M]. 北京: 高等教育出版社, 2004. |
| [2] | 龙驭球, 包世华. 结构力学教程:Ⅰ, Ⅱ[M]. 北京: 高等教育出版社, 2001. |
| [3] | Harry H. West, Luis F. Geschwindner, Fundamentals of Structural Analysis, 2nd Edition[M]. John Wiley & Sons, Inc. February 7th 2002. |
| [4] | Lee K., Uang C.M., Gilbert A.M.. Fundamentals of Structural Analysis[M]. 5th International Edition. McGraw-Hill, 2011. |
| [5] | Aslam Kassimali. Structural Analysis[M]. 5th International Edition. CENGAGE Learning Custom Publishing, 2014. |
| [6] | Hyo Seon Park, Eunseok Lee, Se Woon Choi, et al. Genetic-algorithm-based minimum weight design of an outrigger system for high-rise buildings[J]. Engineering Structures, 2016(117): 496–505. |
| [7] | Amir Fam, Tarek Sharaf, Pedram Sadeghian. Fiber Element Model of Sandwich Panels with Soft Cores and Composite Skins in Bending Considering Large Shear Deformations and Localized Skin Wrinkling[J]. Journal of Engineering Mechanics, 2016, 142(5): 1–14. |
 2018, Vol. 27
2018, Vol. 27

