混凝土结构原理是土木工程专业的一门重要课程^[1-2]，是专业平台课。掌握该课程可以为建筑结构设计、房屋建筑抗震和高层建筑等后续课程打下坚实的理论基础。课程本身概念多，计算公式多，构造措施多，加之学习该课程需要具有一定的力学理论基础，一旦材料力学和结构力学相关知识没有掌握好，学习将困难重重^[3-4]。

构件正截面承载力部分是混凝土结构原理课程的核心内容。此次研究总结出钢筋混凝土构件正截面承载力问题，强调绘制正截面的计算简图及相关参数，借助力和力矩平衡的力学知识推导各种类型的正截面计算公式，建立图与类型的对应关系，以帮助学生更好地理解和掌握该课程。

钢筋混凝土构件的正截面是指与构件纵向长度方向相垂直的截面。钢筋混凝土构件正截面承载力计算的类型因承受内力、截面形式和配筋方式的不同而不同。

正截面承载力计算类型以及对应的破坏类型较多。对于不同的受力构件而言，即便构件的截面形式不同，但其构件所允许的破坏方式具有唯一性，比如受弯构件，正截面的类型有单筋矩形、双筋矩形、T形截面，但是这3种正截面可能发生的破坏类型有少筋梁、适筋梁和超筋梁^[5]三种。但适筋梁的破坏类型既能充分发挥材料的强度又能保证构件破坏时具有需要的延性，因此在推导受弯构件的正截面承载力公式时均以适筋梁破坏为基础进行推导。钢筋混凝土各构件的正截面破坏类型及允许破坏类型如表 1。

表 1(Table 1)

表 1 正截面类型、破坏类型及允许破坏类型 构件名称 正截面类型 可能发生的破坏类型 允许破坏类型 受弯 单筋矩形截面 少筋、适筋、超筋 适筋 双筋矩形截面 少筋、适筋、超筋 适筋 T形截面 少筋、适筋、超筋 适筋 受压 轴压 短—长柱 短柱或中长柱 不对称、对称配筋偏心受压 大偏心受压；小偏心受压 大偏心受压；小偏心受压 受拉 轴心受拉 偏心受拉 大偏拉；小偏拉 大偏拉；小偏拉

表 1 正截面类型、破坏类型及允许破坏类型

正截面承载力计算简图是在以下基础上构建的：(1)理想的破坏模式(表 1中允许破坏类型)；(2)三个基本假定(a.平均应变的平截面假定；b.忽略受拉区混凝土参与受力；c.钢筋及混凝土的本构关系)；(3)混凝土受压区为等效矩形应力。

从表 1可以看出，钢筋混凝土构件的正截面类型及允许的破坏类型较多，其承载力的计算公式与正截面类型一一对应，具体的正截面承载力计算公式类型详见表 2。由表 2可知，正截面承载力的计算公式种类较多，而且正截面承载力的计算公式均有其适用范围，因此，如果死记硬背公式很难掌握。为此，在绘制正截面承载力计算简图的基础上，结合正截面上力和力矩平衡推导其对应的公式。该方法对于受弯、偏心受压、偏心受拉均适用，从表 3中的各类构件的正截面计算简图可以看出，每一种类型的计算简图有细微差别，但主体内部基本相同，因此，只要熟练掌握受弯构件单筋矩形截面的正截面承载力计算简图绘制方法，受弯构件的双筋矩形截面以及T形截面、偏心受压、受拉的正截面承载力计算公式推导易如反掌。

表 2(Table 2)

表 2 正截面承载力计算公式类型 构件类型 受弯 受压 受拉 正截面承载力计算公式类型 单筋矩形 双筋矩形 T形 普通轴压 螺旋轴村 不对称配筋大偏心受压 对称配筋大偏心受压 不对称配筋小偏心受压 对称配筋小偏心受压 轴拉 大偏拉 小偏拉

表 2 正截面承载力计算公式类型

表 3(Table 3)

表 3 正截面承载力计算公式类型及其计算简图 正截面类型 正截面图 正截面计算简图 平截面上的力 单筋矩形截面受弯构件 混凝土合压力：a1fcbx 受拉钢筋的拉力：Asfy 双筋矩形截面受弯构件 混凝土合压力：a1fcbx 受拉钢筋的拉力：Asfy 受压钢筋的压力：As′fy′ T形截面受弯构件 Ⅰ类 混凝土合压力：a1fcbf′x 受拉钢筋的拉力：Asfy Ⅱ类 混凝土合压力：a1fcbx+a1fc(b′f-b)h′f 受拉钢筋的拉力：Asfy 大偏心受压 混凝土合压力：a1fcbx 受拉钢筋的拉力：Asfy 受压钢筋的压力：As′fy′ 外压力：N 小偏心受压 混凝土合压力：a1fcbx 受拉钢筋的拉力：Asσs 受压钢筋的压力：As′fy′ 外压力：N 大偏心受拉 混凝土合压力：a1fcbx 受拉钢筋的拉力：Asfy 受压钢筋的压力：As′fy′ 外拉力：N 小偏小受拉 受拉钢筋的拉力：Asfy 受压钢筋的压力：As′fy′ 外拉力：N 注：混凝土合压力大小可以想象为计算一个棱柱体的体积，即受压区即正截面图中阴影面积为底面积，a1fc为高。

表 3 正截面承载力计算公式类型及其计算简图

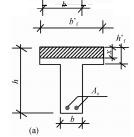
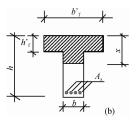
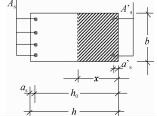
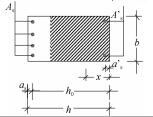
钢筋混凝土构件的正截面是指与构件纵向长度方向相垂直的截面。受弯构件即为梁、板，这两类构件通常水平放置，因此，与受弯构件纵向长度相垂直的截面即为垂直截面。受压构件即为柱，通常竖直放置，因此其正截面为水平截面。在建构各类正截面计算简图时，主要想象该构件是何种构件，一般如何放置，这样就很容易绘制出正截面，然后再根据受力情况画出混凝土受压区域，以阴影面积表示。

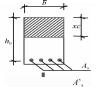
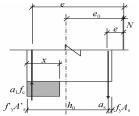
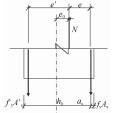
承载力计算简图均从构件的侧面去看，在计算简图中有5大要素需要表达。

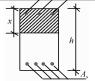
(1) 正截面。正截面是与构件纵向长度方向相垂直的截面。在计算简图中相当于把构件从内力较大与纵向长度相垂直处截开(想象截断的一段丢掉)，并从构件的侧面看，这个正截面即用一根线段，因此，计算简图中正截面即为一根线段表示。

(2) 截断线。构件被正截面截断成两半，其中半截留下，从侧面看构件还是过长，因而再用截断线把构件过长的截断。

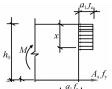
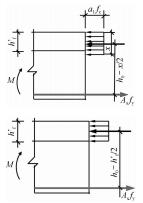
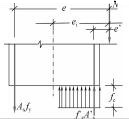
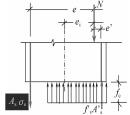
(3) 内力。计算简图中的内力画在截断线一侧。计算简图中的内力对应不同的构件一般有三种：受弯构件的内力是弯矩，正弯矩顺时针，负弯矩逆时针；受压构件的内力是压力即指向正截面，大偏心受压时压力作用在截面以外，小偏心受压时压力作用在截面以内；受拉构件的内力是拉力，即远离截断线，大偏心受拉时拉力作用在受拉和受压钢筋之外，小偏心受拉时拉力作用在受拉和受压钢筋之内。

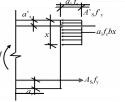
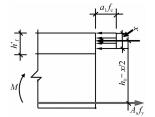
(4) 材料的抵抗力。混凝土、钢筋的抵抗力是绘制在表示正截面处的线段一侧。一般构件材料抵抗力有混凝土受压的压应力、受拉钢筋的拉力和受压钢筋的压力。混凝土压应力按压力合力作用点，以及压力合力大小不变条件等效为矩形应力图形，混凝土压力的合力大小为a₁f_cb_x；除小偏心受压构件外，其余的构件破坏时受拉钢筋均已经屈服，故受拉钢筋的拉力为A_sf_y，在受压区配置有受压钢筋时其压力为A′_Sf′_y。

(5) 正截面的几何尺寸。正截面承载力计算简图中的几何尺寸包括截面的宽度b、高度h、混凝土受压区高度(等效后的)x及截面的有效高度h₀等。对于受压构件还要标出压力(若是受拉构件则标注出拉力)到受拉钢筋、受压钢筋以及截面形心的距离，分别用e、e′和e_i表示。

所有正截面承载力计算公式均依据承载力计算简图(表 3)中力平衡和弯矩平衡(一般以受拉钢筋取矩或者受压区混凝土合力点取矩)推导而得，见表 4。

表 4(Table 4)

表 4 正截面承载力计算公式类与限制条件 正截面类型 计算公式 公式限制条件 单筋矩形截面受弯构件 a1fcbx=Asfy Mu=a1fcbx(h0-0.5x)=Asfy(h0-0.5x) x≤ξbh0防超筋 As≥As, min=ρminbh防少筋 双筋矩形截面受弯构件 a1fcbx+A′sf′y=Asfy Mu=a1fcbx(h0-0.5x)+A′sf′y(h0-a′x) x≤ξbh0防超筋 x≥2a′s保证受压钢筋屈服 T形截面受弯构件 1类 a1fcb′x=Asfy Mu=a1fcb′fx(h0-0.5x) x≤ξbh0防超筋, 通常能满足可不验算 As≥As, min=ρminbh防少筋 2类 a1fc(b′f-b)h′f+a1fcbx=Asfy Mu=a1fc(b′f-b)h′f(h0-0.5h′f)+a1fcbx(h0-0.5x) x≤ξbh0防超筋 As≥As, min=ρminbh防少筋, 通常能满足可不验算 大偏心受压 Nu=a1fcb′f+A′sf′y-Asfy Nue=a1fcbx(h0-0.5x)+A′sf′y(h0-a′s) x≤ξbh0防超筋 x≥2a′s保证受压钢筋屈服 小偏心受压 Nu=a1fcb′fx+A′sf′y-σsfy Nue=a1fcbx(h0-0.5x)+A′sf′y(h0-a′s)或 Nue′=a1fcbx(0.5x-a′x)+A′sf′y(h0-a′s) - 大偏心受拉 Nu=Asfy-A′sf′y-a1fcb′fx Nue=a1fcbx(h0-0.5x)+A′sf′y(h0-a′s) x≤ξbh0防超筋 x≥2a′s保证受压钢筋屈服 小偏小受拉 Nue=A′sf′y(h0-a′s) Nue′=fsAs(h0-as)

表 4 正截面承载力计算公式类与限制条件

为了保证构件正截面能够发生有延性的理想破坏模式(小偏心受压及轴心受压除外)，以及受压区钢筋能够屈服，各正截面计算公式均有相应的限制条件。这些相应的限制条件也是保证对应正截面出现表 1中允许的破坏模式，从而避免出现其他非延性的破坏模式。在教学中强调这些限制条件对于学生掌握不同构件正截面设计计算，保证构件最终出现理想的破坏模式具有重要意义。

由表 3的正截面承载力的计算简图可以看出，其他类型正截面承载力的计算简图与单筋矩形截面的材料抵抗图相比，增加了受压钢筋的压力，而在内力方面则需要结合不同类型的内力情况进行绘制，因此只要掌握了单筋矩形截面受弯构件的正截面承载力计算简图，其他类型较容易绘制。根据绘制出的计算简图，再根据力和弯矩平衡即可推导出正截面承载力计算的公式，不同类型正截面的承载力计算公式的推导的方法均相同，并在教学中强调为了实现设计的构件正截面出现理想的破坏模式，则必须充分掌握各构件正截面承载力公式的限制条件。笔者所倡导的方法不需要死记硬背数量众多的公式，不会让学生在学习过程中产生畏难情绪，可帮助提高学习效率，从而达到理想的教学效果。