作为中国土木工程领域目前应用最多、范围最广的结构形式,混凝土结构在建筑结构中占据着越来越重要的位置[1],混凝土结构课程也已成为土木工程专业的主干课程[2]。针对中外合作办学,一些机构全面引入国外合作机构的课程和考核标准,照搬国外教材和教学模式,未考虑国内实际情况。而一些机构将课程的实施依赖于普通二级学院,师资以普通二级学院的师资为主,课程实施与国内专业课一致。这些现状都反映出中外合作办学的混凝土结构课程存在中外各自独立或全盘引进国外教学课程的问题,未发挥“合作”的优势。
因此,有必要在合作共赢的目标下,进行课程的中外结合。针对混凝土结构课程,其计算原理相通而方法和系数中外有所不同。通过对比,分析课程知识点异同,提炼中外不同方法的优劣,达到引进国外资源并吸收转化为中国所用的中外合作办学目标。文章以中外合作办学本科机构——浙江科技学院中德工程师学院为例,对混凝土结构课程承载力计算的重点内容进行中方和德方的知识点对比分析,为土木工程专业中德合作办学提供参考,推进中外合作办学,引进并吸收、转化国外教学资源。
一、作用效应组合承载力计算首先要确定荷载作用,进行荷载作用效应组合。中德双方均按2种极限状态分别确定效应组合方法,即承载力极限状态(Grenzzuständen der Tragfähigkeit, GZT)和正常使用极限状态(Grenzzustände der Gebrauchsfähigkeit, GZG),其中抗弯、抗剪等承载力计算属于承载力极限状态,裂缝宽度、变形验算属于正常使用极限状态。在承载力极限状态和正常使用极限状态下,中德双方荷载作用效应的组合方式和系数有所不同。
(一) 承载力极限状态中方承载力极限状态需满足γ0≤R,其中R为结构构件抗力设计值,γ0为结构重要性系数,S为荷载效应设计值。德方承载力极限状态需满足Ed≤Rd,其中Rd为结构构件抗力设计值,Ed为荷载效应设计值,计算思路与中方保持一致。该极限状态的作用效应组合,中德双方均分为2种情况,一是持久设计状况和短暂设计状况,另一个是地震等不寻常荷载设计状况。
在持久设计状况和短暂设计状况下,中方分别计算由可变荷载控制和由永久荷载控制的效应组合值见式(1)、式(2),取其较大值作为荷载效应设计值S,而德方只采用等同于中方可变荷载控制的组合作为荷载效应设计值Ed,式(3)。
| $ S = {\gamma _G}{S_{GK}} + {\gamma _{Q1}}{S_{Q1K}} + \sum\limits_{i = 2}^n {{\gamma _{Qi}}{\varphi _{ci}}{S_{QiK}}} $ | (1) |
| $ S = {\gamma _G}{S_{GK}} + \sum\limits_{i = 1}^n {{\gamma _{Qi}}{\varphi _{ci}}{S_{QiK}}} $ | (2) |
| $ {E_d} = E\left[ {\sum\limits_{j \ge 1} {{\gamma _{Gj}}{G_{kj}}} + {\gamma _{Q1}}{Q_{K1}} + \sum\limits_{i > 1} {{\gamma _{Qi}}{\psi _{0i}}} {Q_{Ki}}} \right] $ | (3) |
式中:γG、γGj为永久荷载分项系数,γQ、γQi为可变荷载分项系数,SGK、Gkj为永久荷载标准值,SQiK、Qki为可变荷载标准值,φci、ψ0i为可变荷载组合值系数。
中德双方的荷载分项系数如表 1所示,可变荷载组合值系数如表 2所示。可以看到,此状态下德方的荷载组合相当于中方的可变荷载控制组合,但永久荷载分项系数和可变荷载分项系数比中方大,且可变荷载组合值系数除海拔小于1 000 m地区雪/冰荷载外,均大于相应的中方取值,因此,相同荷载标准值下,德方最终荷载效应设计值比中方大。若将德方荷载组合与中方永久荷载控制组合相比,虽永久荷载分项系数相同,但由于中方对所有可变荷载均乘以小于1的可变荷载组合值系数,荷载组合中的活荷载项比德方小,因此,德方最终荷载效应设计值更大,设计更保守。
| 表 1 荷载分项系数(持久和短暂设计状况) |
| 表 2 可变荷载组合值系数 |
在地震等不寻常荷载设计状况下,中方荷载效应由地震等可变荷载控制,则中方与德方荷载效应组合分别为式(1)和式(3)。此时,中方荷载分项系数不小于1.0,而德方荷载分项系数均为1.0(表 3),即德方认为地震等不寻常荷载不经常发生,德方最终荷载效应设计值一般比中方小。
| 表 3 荷载分项系数(地震等不寻常荷载设计状况) |
中方正常使用极限状态需满足S≤C,德方需满足Ed≤Cd,其中C、Cd为结构构件达到正常使用状态所规定的变形、应力、裂缝宽度和自振频率等的限值,S、Ed为荷载效应设计值。此时荷载作用效应组合分3种情况,如表 4所示。
| 表 4 正常使用极限状态对比 |
其中,φci、ψ0i为可变荷载组合值系数,φf1、ψ11为可变荷载频遇值系数,φqi、ψ2i为可变荷载准永久值系数,分别如表 5所示。
| 表 5 可变荷载组合值、频遇值、准永久值系数 |
由表 4、表 5可以看到,对于正常使用极限状态荷载效应组合的3种情况,中德计算方法是一致的,但频遇值、准永久值系数有所差别,对于楼面活荷载(住宅、宿舍、旅馆、办公楼、集会区、商场、仓库),德方系数比中方大,对于雪/冰荷载、风荷载、非火灾温度作用,德方系数比中方小。因此,尽管正常使用极限状态中德双方计算方法相同,但最终荷载效应设计值大小不定。
2种极限状态下中德双方荷载效应设计值的计算方法基本相同,德方在荷载组合时,对偶然荷载(地震、风荷载、雪/冰荷载等)考虑较少,比重比中方小,而对于常遇荷载(楼面活荷载、恒载等)考虑较多,比重比中方大。
二、正截面受弯承载力计算结构梁板等构件在外力作用下受弯,需进行受弯承载力计算,使截面受弯承载力大于构件的弯矩荷载效应。针对弯矩效应计算,中德双方均按永久荷载满跨布置和活荷载最不利布置计算截面最不利弯矩。针对弯矩效应分析,均采用弹性分析、塑性内力重分布的弯矩调幅分析、弹塑性分析这3种方法,但其中弯矩调幅有所不同,中方只规定了梁负弯矩调幅不超过20%,板负弯矩调幅不超过25%[3-4],德方则根据弯矩系数μEds来确定弯矩调幅程度[5]。
| $ {\mu _{Eds}} = {M_{Eds}}/(b{d^2}{f_{cd}}) $ | (4) |
式中:MEds为弯矩效应,b、d分别为截面宽度和有效高度,fcd为混凝土抗压强度。
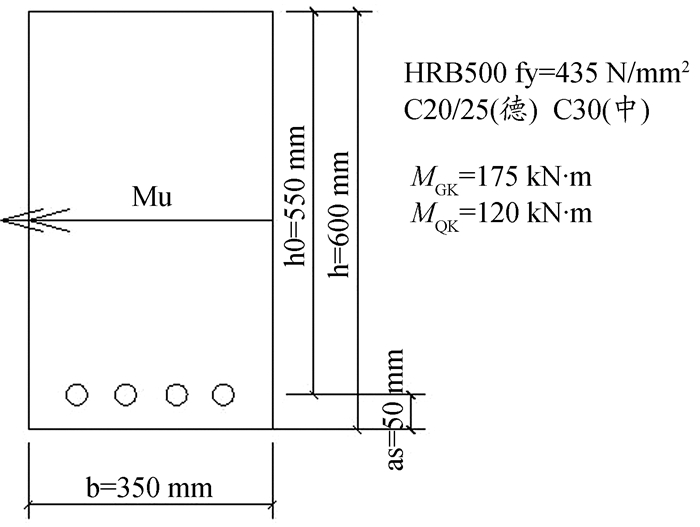
针对正截面受弯承载力计算,以一个例子说明中德计算方法的不同。梁截面如图 1所示,永久荷载弯矩标准值MGK=175 kN·m,可变荷载弯矩标准值MQK=120 kN·m,确定截面抗弯钢筋配筋。
|
图 1 正截面抗弯承载力计算示例 |
弯矩效应MEds=1.35×175+1.5×120=416.25 kN·m,μEds, lim=0.371,计算过程如表 6所示。
| 表 6 正截面受弯承载力的德方计算方法 |
弯矩效应M=max(1.35×175+1.4×0.7×120, 1.2×175+1.4×120)=378 kN·m,混凝土受压区高度
德方利用查图法,即首先根据弯矩效应和截面特征计算弯矩系数μEds,然后根据预先制好的μEds与其他参数的关系图得到混凝土相对受压区高度、压力合力作用点,计算所需配筋,但取值误差较大,精度不高。此外,德方还将一系列弯矩系数μEds与混凝土受压区椭圆面积系数ω的关系制成表(ω方法),根据计算得到实际弯矩系数μEds,查表即可得到混凝土受压区面积即合压力,验算弯矩系数限值保证受拉钢筋屈服,计算截面抗弯钢筋,或采用kd方法,根据系数kd与系数ks的关系确定截面配筋。
中方正截面受弯承载力则采用直接计算的方法,根据截面力平衡和力矩平衡,计算截面拉力,从而计算截面抗弯受拉钢筋,同时验算混凝土受压区高度小于超筋破坏界限受压区高度,保证受拉钢筋能屈服,并验算最小配筋率,保证少筋破坏不会发生。
由此可见,在计算混凝土受压区时,中方将混凝土受压区应力分布等效为矩形,可根据截面力平衡和力矩平衡直接计算而无需积分或迭代。德方在混凝土受压区为长方形的情况下并未采用等效矩形,而是为了计算方便,事先将混凝土受压区椭圆面积跟弯矩效应的关系制成图或表,参照图表得到配筋计算系数,从而计算截面抗弯配筋(只有在混凝土受压区为梯形变截面时难以事先编制系数表格,才将混凝土受压区应力分布等效为矩形[6])。德方采用应力实际分布更符合实际情况,但计算时需查图表,操作繁琐且精度依赖于操作者经验。
三、正截面受压承载力计算柱、墙等竖向构件在外力作用下受压,需要进行正截面受压承载力计算。在计算混凝土构件正截面受压承载力时,中德双方均分为轴心受压和偏心受压2种情况。
(一) 二阶效应的考虑中方按轴心受压和偏心受压分别判断是否考虑二阶效应。对于轴心受压构件,并不强调二阶效应,而是按长细比确定稳定系数φ,乘以截面材料确定的轴心力Acfc+Asfy,得到截面轴心受压承载力N=0.9φ(Acfc+Asfy)(0.9是考虑初始偏心和轴心受压构件可靠度影响的折减系数),当φ<1时,截面轴压承载力小于材料确定的轴心力,即认为考虑了稳定问题的二阶效应。对于偏心受压构件,若长细比大于考虑两端弯矩的临界长细比,则强调考虑二阶效应,由端弯矩乘以弯矩增大系数、偏心距调节系数得到二阶效应产生的控制截面弯矩M,根据控制截面弯矩计算力矩偏心距e0,从而根据截面力平衡和力矩平衡计算正截面偏压承载力或配筋。
德方则不论轴心受压还是偏心受压,均按临界长细比确定是否考虑二阶效应。当长细比大于临界长细比时考虑二阶效应,对偏心距附加一个考虑长细比、压力、长期效应的二阶效应偏心距,根据增大后的偏心距计算控制截面弯矩MEd和正截面压力NEd、截面偏心方向边长h、截面宽度b计算弯矩系数μEd、压力系数νEd,由事先制好的一系列M-N相关曲线查找相应的系数ωtot,从而得到总的受压钢筋
可以看到,中德双方均是以增大控制截面弯矩考虑偏心受压二阶效应,但中方根据截面力平衡与力矩平衡直接计算,而德方则根据事先制好的M-N相关曲线查找参数得到。计算轴心受压时,中方以稳定系数折减承载力,而德方仍采用与偏心受压相同的方法。相比而言,中方的实用性更强,不需参考图表,但理论意义模糊,而德方计算原理性更清晰,但需参考图表,操作起来较为复杂。
(二) 计算长度的确定确定受压构件计算长度时,中德双方均分为无侧移构件和有侧移构件2种,但区别是中方直接按楼盖类型、受压构件位置(底层或上部楼层)给定了柱的计算长度[3],而德方则按无侧移构件和有侧移构件,根据两端支承条件(简化计算)或柱上下端的梁柱刚度比(准确计算)确定长度系数。相比而言,中方计算更实用,德方计算分类细,更为精确但更繁琐。
(三) 大小偏压判断中方在偏心受压构件正截面受压承载力计算时,根据界限受压区高度ξb判断截面的大小偏压,从而按截面受压钢筋是否屈服计算钢筋应力(大偏压屈服、小偏压不屈服),而德方在计算中则按初始偏心距e0与截面偏心方向边长h的比值判断是属于受压构件还是受弯构件:e0/h < 3.5为受压构件,类似于中方小偏压构件;e0/h≥3.5为受弯构件,类似于中方大偏压构件。
四、斜截面受剪承载力计算混凝土构件剪力较大时会产生斜截面受剪破坏,需要计算斜截面受剪承载力,中德双方在计算时有所不同。
(一) 计算跨度和剪力设计值的确定中方曾在2002规范中[7]按构件类型、支承刚度等对计算跨度做了具体规定,而在2010规范中[4]则只说明计算跨度按支承中心距或净距取定,并根据支承节点刚度、反力位置加以修正,剪力设计值为计算跨度下的最大剪力,一般为支座边缘处剪力。
德方则按直接支承和间接支承区分支座条件,认为直接支承构件由于支座部位混凝土形成斜向受压柱抗剪,不需计算抗剪钢筋,计算跨度不计支座部位混凝土斜向受压柱的范围,剪力设计值从离开支座边缘有效高度d处计算,而间接支承则由于不会形成混凝土斜向受压柱,需将支座边缘最大剪力作为剪力设计值。
(二) 计算方法中德双方斜截面受剪承载力的计算均由桁架模型的力平衡推导得到,但中方还考虑了混凝土对抗剪承载力的贡献,而德方则忽略了这一项承载力,设计更保守。以一个例子说明计算方法的异同,如图 2所示,根据外荷载和截面条件确定抗剪箍筋配置。计算方法与步骤如表 7所示。

|
图 2 斜截面受剪承载力计算示例 |
| 表 7 斜截面受剪承载力计算方法对比 |
可以看到,中德双方斜截面受剪承载力计算第一步都是确定剪力设计值,但剪力值有所不同。德方由于为直接支承支座,计算跨度不计混凝土斜压柱范围,而是离开支座边缘有效高度d间的跨度。由于剪力从支座到跨中逐渐减小,故所取计算跨度范围内的最大剪力设计值比支座处剪力值小。与德方直接支承支座相对应,中方为现浇节点,计算跨度为支座净跨,剪力设计值为支座边缘处剪力,因此尽管中方均布荷载效应比德方小,但剪力设计值大。然后,中德双方都进行了抗剪截面的验算,即混凝土斜向受压提供的抗剪承载力要大于剪力设计值,否则截面易发生脆性剪切破坏。最后都根据剪力设计值计算抗剪钢筋,此时德方不考虑混凝土对抗剪承载力的贡献,尽管剪力设计值小,计算得到的抗剪钢筋面积却比中方计算大,设计更保守。
五、结语从上述对比可知,中德双方在作用效应、正截面受弯、正截面受压、斜截面受剪承载力方面的计算原理相同,但实际计算方法有所差别。总的而言,德方计算方法较为精确,但操作繁琐,中方方法更为实用,但近似和假定较多,精确度比德方低。在中外融合教学中,应从计算原理出发,介绍德方原理性较强的精确方法,并结合中方实用方法,加深对计算原理的理解,通过对比掌握中德双方计算方法,加强知识的多元化理解和融会贯通。在后续研究中,对出现率低的抗扭、抗冲切、局部受压承载力和正常使用的裂缝变形验算进行对比研究,通过对比重要知识点,推进中外合作办学,引进、吸收、转化国外资源,促进中外合作办学融合教学的发展。
| [1] |
闫学恭. 钢筋混凝土结构在建筑工程中的重要作用[J]. 现代装饰(理论), 2013(3): 157. |
| [2] |
杜喜凯, 朱建波, 郝文秀, 等. 混凝土结构课程设计的改革与探讨[J]. 东南大学学报(哲学社会科学版), 2012(Sup2): 115-116. |
| [3] |
建筑结构荷载规范: GB 50009-2012[S].北京: 中国建筑工业出版社, 2012.
|
| [4] |
混凝土设计规范: GB 50010-2010[S].北京: 中国建筑工业出版社, 2010.
|
| [5] |
Tragwerke aus Beton, Stahlbeton und Spannbeton-Teil 1: Bemessung und Konstruktion: DIN 1045-1[S]. Deutsches Institut für Normung, 2008.
|
| [6] |
Schneider K J, Goris A. Bautabellen für Ingenieure mit Berechnungshinweisen und Beispielen[M]. Köln: Werner Verlag, 2012.
|
| [7] |
混凝土设计规范: GB 50010-2002[S].北京: 中国建筑工业出版社, 2002.
|
 2018, Vol. 27
2018, Vol. 27

