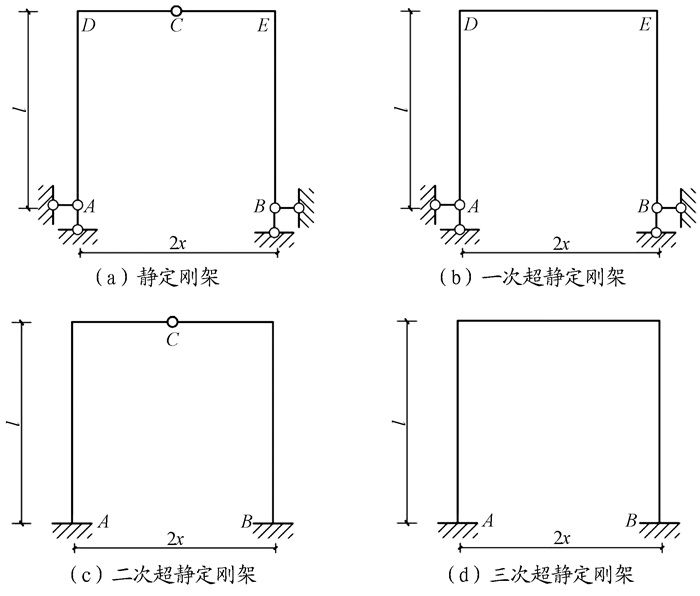
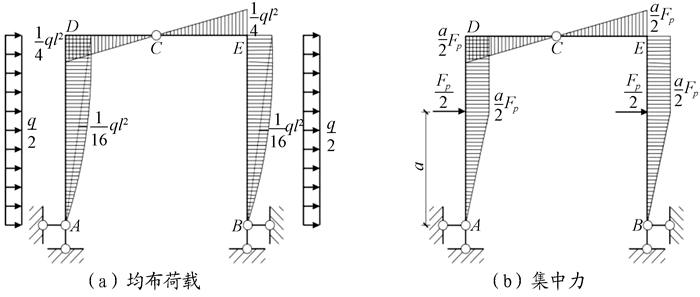
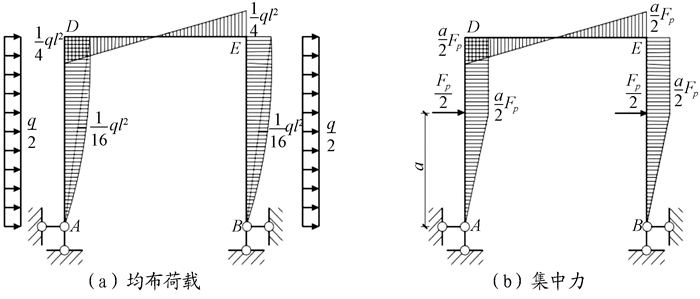
“万丈高楼平地起”, 这表明了打下好基础的重要性。结构力学是土木工程专业最重要的专业基础课之一, 为后续钢筋混凝土结构、钢结构、高层结构等课程提供荷载效应即结构的内力图, 其教学效果的关键性不言而喻。但是, 很多学生对结构内力分析感到困惑, 特别是超静定结构的内力, 严重影响了学生对课程的学习兴趣[1-3]。以简化计算、调动学生学习结构力学的积极性、提高结构力学教学效果为目的, 求解绘制了图 1中4组刚架在侧向受反对称荷载(均布荷载、集中力)作用时的弯矩图。通过对比不同刚架受相同荷载作用时的弯矩图, 分析相应弯矩图的特点, 找出各弯矩图之间的规律, 并加以归纳总结, 帮助学生更好地理解并快速绘制对称刚架的弯矩图。图 1中, 2x为刚架的跨度, l为刚架的高度。
|
图 1 4组刚架 |
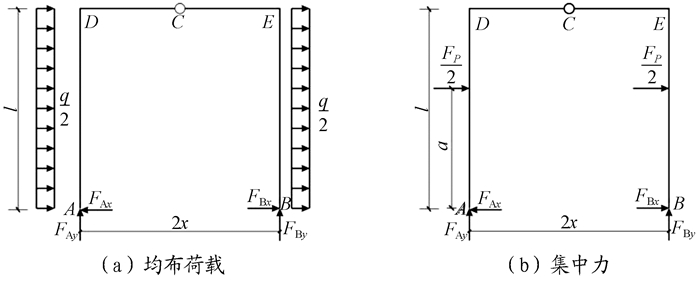
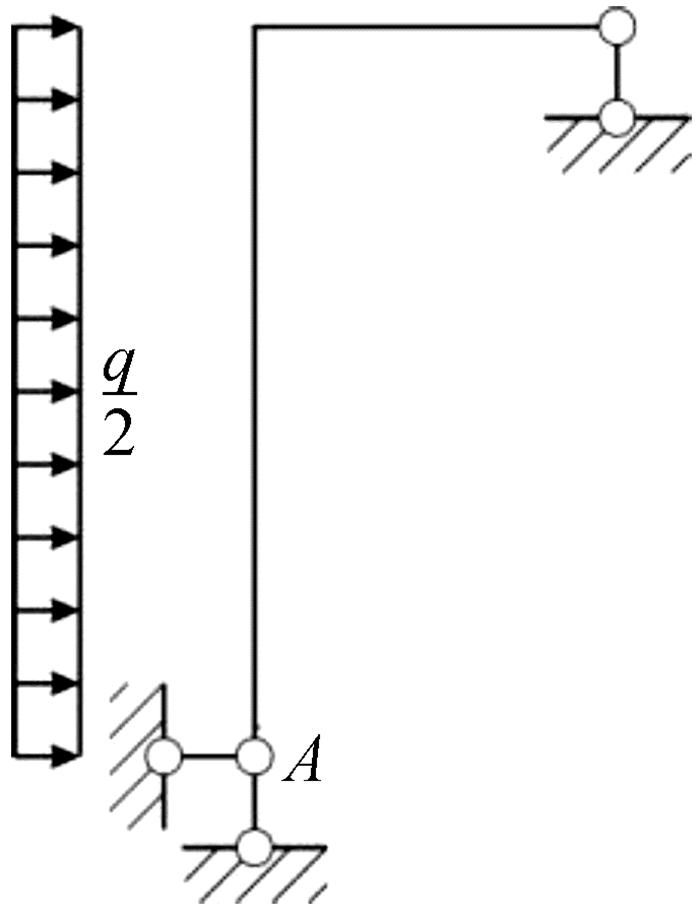
刚架在反对称均布荷载q和集中力Fp作用下的计算简图, 如图 2所示。其中, a为集中力与支座间的竖向距离。
|
图 2 计算简图 |
在反对称均布荷载作用下, 对图 1(a)中静定刚架进行受力分析, 列整体对B点的力矩平衡方程为
| $ \sum {M_B} = 0, 得{F_{{\rm{Ay}}}} = - \frac{{q{l^2}}}{{4x}}( \downarrow ) $ | (1) |
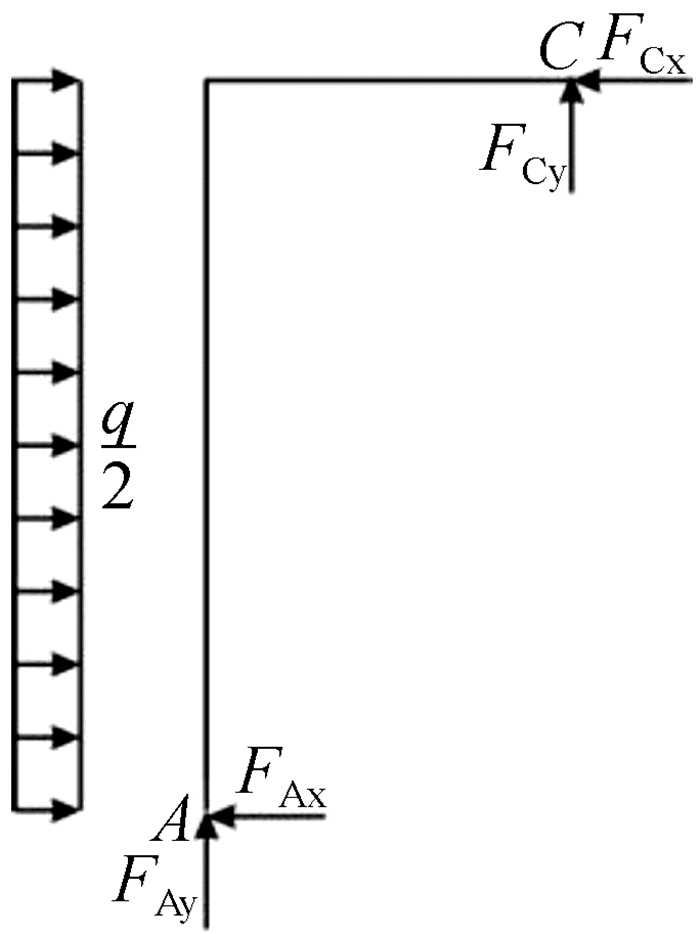
左半侧隔离体如图 3所示, 依据对C点的力矩平衡及水平方向力整体投影平衡求得
|
图 3 左半侧隔离体 |
| $ \sum {M_C} = 0, 得{F_{{\rm{A}}x}} = \frac{{ql}}{2}\left( \leftarrow \right);\sum {F_x} = 0, 得{F_{{\rm{B}}x}} = - \frac{{ql}}{2}\left( \leftarrow \right) $ | (2) |
其弯矩图如图 4(a)所示。同样地, 图 1(a)中静定刚架在反对称集中力作用下, 采用类似的方法可求得水平支座反力为
|
图 4 静定刚架弯矩图 |
| $ {F_{{\rm{A}}x}} = \frac{{{F_p}}}{2}\left( \leftarrow \right), {F_{{\rm{B}}x}} = - \frac{{{F_p}}}{2}\left( \leftarrow \right) $ | (3) |
其弯矩图如图 4(b)所示。
二、一次超静定对称刚架在反对称均布荷载作用下, 图 1(b)中的一次超静定对称刚架, 由于结构正对称、荷载反对称, 可取半结构, 如图 5所示[4]。
|
图 5 半结构 |
图 5为静定结构, 由x方向力投影平衡求得FAx=ql/2(←), 其弯矩图如图 6(a)所示。
|
图 6 一次超静定刚架弯矩图 |
同样, 图 1(b)中一次超静定刚架在反对称集中力作用下, 采用类似的方法可求得水平支座反力FAx=Fp/2(←), 对应的弯矩图如图 6(b)所示。
反对称荷载作用下静定与一次超静定刚架的弯矩及支座反力对比, 如表 1所示。
| 表 1 静定与一次超静定刚架弯矩及反力对比 |
对比图 6和图 4并结合表 1可知, 在反对称荷载作用下, 一次超静定对称刚架与静定对称刚架的水平支座反力相同, 均为外部荷载的一半, 且与跨度2x无关, 即无论跨度多大, 水平支座反力均为外部荷载的一半。同时, 对于底部为固定铰支座的刚架, 其水平支座反力是控制弯矩分布的关键因素, 由水平支座反力可以直接绘制出弯矩图。反对称荷载作用下一次超静定对称刚架与静定对称刚架的水平支座反力相同, 故二者的弯矩图相同。例如, 在反对称均布荷载作用下, 静定对称刚架的水平支座反力FAx=ql/2, 一次超静定对称刚架的水平支座反力FAx=ql/2, 表明二者的水平支座反力相同, 二者的弯矩图也相同。
三、二次超静定对称刚架在反对称均布荷载作用下, 图 1(c)中的二次超静定对称刚架, 由于结构正对称、荷载反对称, 可取半结构, 如图 7(a)所示。
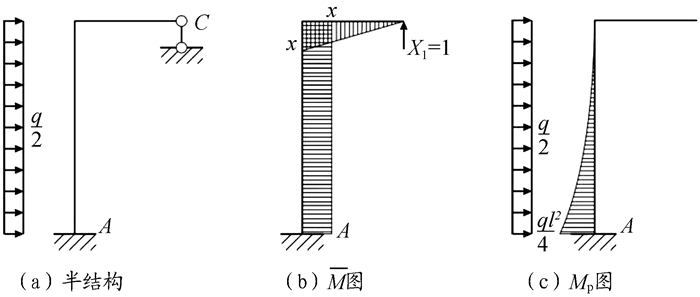
|
图 7 半结构及弯矩图 |
由x方向力投影平衡, 求得水平支座反力FAx=ql/2(←)。
取悬臂刚架为此半结构的力法基本结构, 则力法典型方程为
| $ {\delta _{11}}{X_1} + {\mathit{\Delta }_{{\rm{1P}}}} = 0 $ | (4) |
虚设单位力下的M图如图 7(b)所示, MP图如图 7(c)所示。利用图乘法求得柔度系数δ11与自由项Δ1P为
| $ {\delta _{11}} = \frac{{3{x^2}l + {x^3}}}{{3EI}}, {\mathit{\Delta } _{{\rm{1P}}}} = - \frac{{qx{l^3}}}{{12EI}} $ | (5) |
由式(4)求得
| $ {X_1} = \frac{{q{l^3}}}{{12xl + 4{x^2}}}, {M_{\rm{A}}} = \frac{{2q{l^3} + q{l^2}x}}{{4x + 12l}} $ |
根据对称性可绘制其弯矩图, 如图 8(a)所示。同样, 图 1(c)中的二次超静定对称刚架在反对称集中力作用下, 采用类似的方法可求得水平支座反力和支座A处的端弯矩为
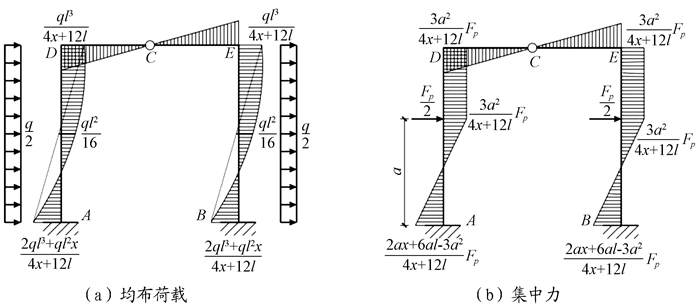
|
图 8 二次超静定刚架弯矩图 |
| $ {F_{{\rm{A}}x}} = \frac{{{F_p}}}{2}\left( \leftarrow \right), {M_{\rm{A}}} = \frac{{2ax + 6al - 3{a^2}}}{{4x + 12a}}{F_{\rm{P}}} $ | (6) |
其弯矩图如图 8(b)所示。
四、三次超静定对称刚架在反对称均布荷载作用下, 图 1(d)中的三次超静定对称刚架, 可取半结构, 如图 9(a)所示。
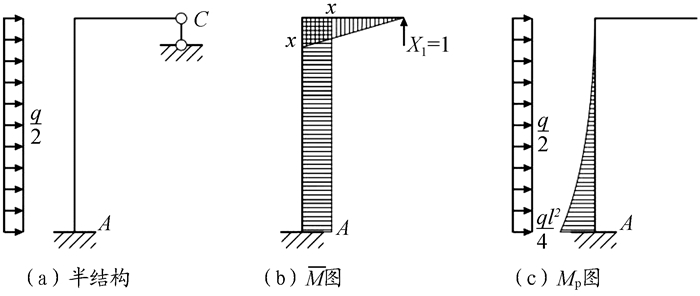
|
图 9 半结构及弯矩图 |
由x方向力投影平衡, 求得水平支座反力FAx=ql/2(←)。
取悬臂刚架为此半结构的力法基本结构, 则力法典型方程为
| $ {\delta _{11}}{X_1} + {\mathit{\Delta }_{{\rm{1P}}}} = 0 $ | (7) |
虚设单位力下的M图如图 9(b)所示, MP图如图 9(c)所示。利用图乘法求得柔度系数δ11与自由项Δ1P为
| $ {\delta _{11}} = \frac{{3{x^2}l + {x^3}}}{{3EI}}, {\mathit{\Delta }_{1{\rm{P}}}} = - \frac{{qx{l^3}}}{{12EI}} $ | (8) |
由式(7)求得
| $ {X_1} = \frac{{q{l^3}}}{{12xl + 4{x^2}}}, {M_{\rm{A}}} = \frac{{2q{l^3} + q{l^2}x}}{{4x + 12l}} $ |
其弯矩图如图 10(a)所示。同样, 图 1(d)中的三次超静定对称刚架在反对称集中力作用下, 采用类似的方法可求得水平支座反力和支座A处的端弯矩为
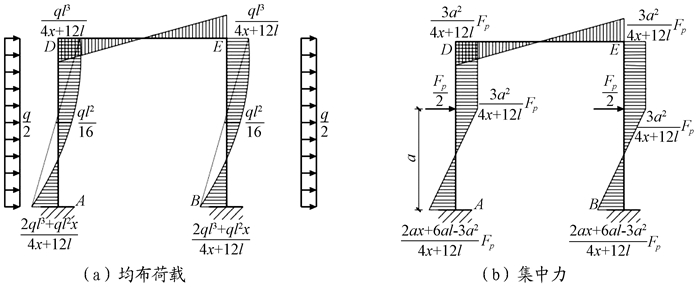
|
图 10 三次超静定刚架弯矩图 |
| $ {F_{{\rm{A}}x}} = \frac{{{F_p}}}{2}\left( \leftarrow \right), {M_{\rm{A}}} = \frac{{2ax + 6al - 3{a^2}}}{{4x + 12a}}{F_P} $ | (9) |
其弯矩图如图 10(b)所示。反对称荷载作用下二次和三次超静定对称刚架的弯矩及支座反力对比, 如表 2所示。
| 表 2 二次与三次超静定对称刚架弯矩及反力对比 |
对比图 10和图 8并结合表 2可知, 在反对称荷载作用下, 三次超静定对称刚架与二次超静定对称刚架的水平支座反力相同, 且与图 4和图 6的水平支座反力也相同, 与跨度2x无关, 均为外部荷载的一半。与固定铰支座的刚架相比, 固定端支座的刚架在支座处增加了端弯矩, 但水平支座反力是相同的, 故弯矩图的整体走向一致。在用半结构法求解时, 三次超静定刚架和二次超静定刚架所取的半结构完全相同, 且所受外荷载也一样, 故二者的水平支座反力相同, 弯矩图也相同。例如, 在反对称均布荷载作用下, 二次超静定对称刚架的水平支座反力FAx=ql/2、支座端弯矩MAD=(2ql3+ql2x)/(4x+12l), 三次超静定对称刚架的水平支座反力FAx=ql/2、支座端弯矩MAD=(2ql3+ql2x)/(4x+12l), 表明二者的水平支座反力、支座固端弯矩均相同, 二者的弯矩图也相同。
五、结语对称结构与反对称荷载是结构力学教学与学习中比较特殊的问题, 其支座反力、弯矩图有较好的规律性。通过4组对称刚架在两类反对称荷载作用时的内力分析发现, 在反对称荷载作用下, 无论是静定对称刚架还是超静定对称刚架, 其水平支座反力都与跨度2x无关, 且均为外部荷载的一半。另外, 支座约束相同的对称刚架在相同的反对称荷载作用下, 弯矩图是相同的。
结构力学是土木工程专业的重要专业基础课, 学生要勤于思考、善于思考, 不要生搬硬套, 要学会举一反三、归纳对比、提炼规律, 从中发现学习结构力学的乐趣, 培养自己分析和解决实际问题的能力, 从而更好地掌握这门课程。
| [1] |
严心池, 盖京波. 结构力学教学核心概念的精细研究——以力法为例[J]. 力学与实践, 2016, 38(4): 453-455. |
| [2] |
许凯, 陈朝峰, 杨祖权. 定性分析在结构力学教学中的应用研究[J]. 高等建筑教育, 2010, 19(6): 98-101. |
| [3] |
程健, 翟清翠, 刘运生. 结构力学教学应用归纳对比法的探索[J]. 高等建筑教育, 2012, 21(3): 111-113. |
| [4] |
龙驭球, 包世华, 袁驷. 结构力学Ⅰ-基本教程[M]. 3版. 北京: 高等教育出版社.
|
 2018, Vol. 27
2018, Vol. 27