b. 中南大学 重载铁路工程结构教育部重点实验室, 湖南 长沙 410075
b. Key Laboratory of Engineering Structures of Heavy Haul Railway(Central South University), Ministry of Education, Central South University, Changsha 410075, P. R. China
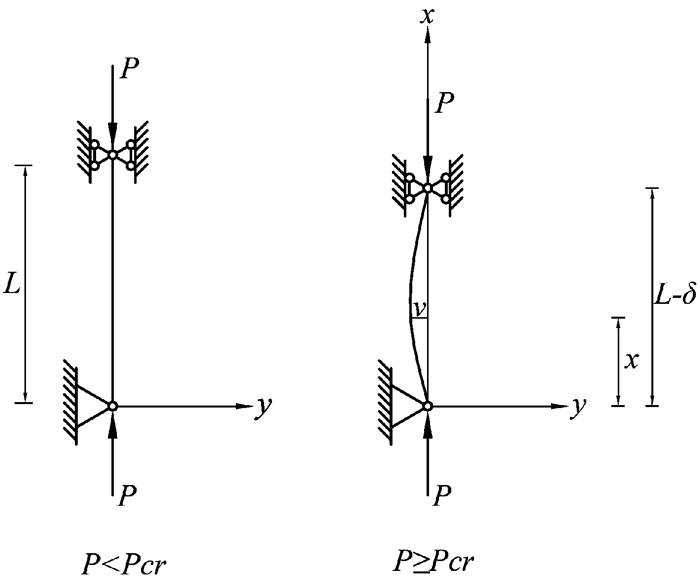
自1744年瑞士著名数学家欧拉(Euler)提出柱子理论以来,工程界已形成共识:柔性受压构件设计必须避免其在服役过程中进入失稳临界状态,即结构永久性地偏离设计状态,构件剩余抗力迅速耗尽直至破坏[1]。经典柱子理论针对理想压杆稳定性分析给出如下描述:“当轴向荷载P较小时,压杆只产生轴向压缩变形。此时,如有一微小横向干扰,压杆就发生微弯。然而一旦解除干扰,压杆立即恢复到原来的直线状态,表明压杆的轴向受压平衡是稳定的。当荷载增加到某一数值Pcr时,微小的干扰使压杆微弯后,再撤去此干扰,压杆仍然保持微弯状态而不恢复到直线位置,这就意味着除了直线平衡外,还存在微弯平衡位置。外力和内力的平衡是随遇的,也称为随遇平衡或中性平衡(Neutral Equilibrium)。当荷载稍大于Pcr时,微小的干扰将使压杆产生急剧发展的弯曲变形,导致压杆破坏。此时,压杆初始直线平衡是不稳定的,如图 1所示,称作压杆屈曲(Buckling)或丧失稳定”[2]。笔者在钢结构设计课程教学中,有学生反映理解上述描述性文字存在如下问题:(1)如何理解荷载P小于临界值Pcr时,横向干扰撤除后压杆恢复直线平衡状态的物理实质?(2)P达到临界值Pcr时,如何解释线性构件的平衡状态不是唯一现象?(3)如何揭示荷载P大于临界值Pcr时压杆失稳破坏机理?问题2的结论来自柱子微弯平衡状态微分方程求解结果[3],问题1和3的结论尽管已被实验证实[4],但柱子理论未给出轴心受压构件力学性能的物理解释。因此,建立分析细长柱从稳定过渡到不稳定状态的直观物理模型,对促进学生和结构工程师掌握弹性结构稳定性判别方法具有积极的现实意义[5-6]。
|
图 1 压杆的分叉屈曲 |
本文借鉴经典结构稳定性理论教科书采用的刚球模型,将弹性细长柱失稳前后受力性能,与刚球在不同外形支撑面上受扰运动状态的变化特征联系起来,建立理想轴心受压构件稳定性分析的直观物理模型,提出结构静力稳定性判别的广义力增量准则,为多自由度弹性系统静力稳定性提供物理解释。
一、理想压杆稳定性分析的等效刚球模型为了与经典教科书的表述一致,假定刚球支撑面的正投影可用抛物线代表[7]:
| $ y = \frac{1}{2}a{x^2} $ | (1) |
不难理解:当a>0时(图 2-a),支撑面‘开口朝上’;当a<0时(图 2-c),支撑面‘开口朝下’;当a=0时(图 2-b),则支撑面退化为平面。
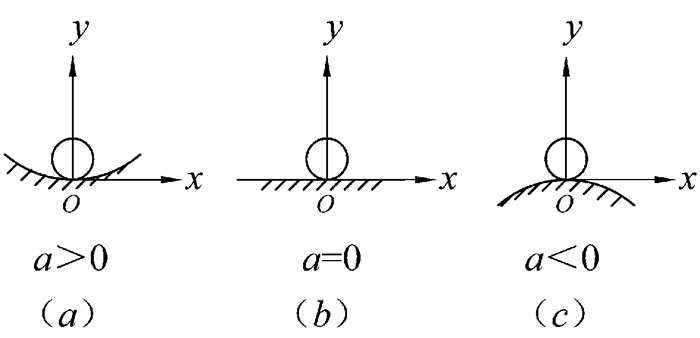
|
图 2 典型支撑面上刚球的初始平衡状态 |
假定刚球初始置于图 2坐标系原点并维持静平衡,取刚球初始平衡位置为势能零点,计算刚球在任意扰动位置的总势能如下:
| $ {\Pi _d} = 0 - \left( { - mg \cdot y} \right) = mg \cdot \frac{1}{a}a{x^2} $ | (2) |
根据能量原理,刚性小球扰动抗力Fc虚功的负值应等于总势能的改变,即有
| $ \delta {\Pi _d} = - {F_c}\delta x = mg \cdot ax \cdot \delta x $ | (3) |
其中,
| $ {F_c} = - mg \cdot ax = - {k_{eq}}x $ | (4) |
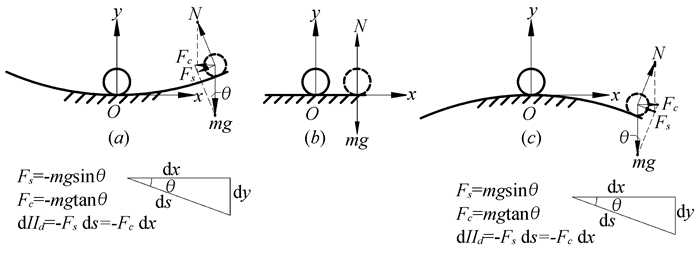
式中,负号表示Fc的正方向与坐标轴正方向一致。式(4)给出的小球扰动抗力可视为与弹簧作用等效,虚拟弹簧常数keq=mga。当a>0时(图 3-a),支撑面下凹,由式(4)亦知,刚球在“正弹簧”(keq>0)作用下将回到初始位置,刚球的初始构型是稳定的;当a<0时(图 3-c),支撑面上凸,刚球在“负弹簧”(keq<0)作用下将偏离初始位置,刚球初始构型是不稳定的;而a=0时(图 3-b),虚拟弹簧(keq=0)不存在,刚球干扰后平衡构型由扰动决定,刚球处于中性平衡。
|
图 3 刚球扰动抗力分析 |
回到理想压杆直线平衡形式稳定性的问题上来。类似的,取压杆直线形式平衡位置为势能零点,则任意扰动位置下压杆的总势能[8]为
| $ {\Pi _d} = \frac{{EI}}{2}\int_0^L {v''{{\left( x \right)}^2}{\rm{d}}x - \frac{P}{2}} \int_0^L {v'{{\left( x \right)}^2}{\rm{d}}x} $ | (5) |
式中,L表示杆长,P表示轴压力,EI表示截面抗弯刚度。对于两端简支的压杆,引入横向变位函数
| $ v\left( x \right) = {v_0}\sin \frac{{\pi x}}{L} $ | (6) |
式中,v0表示变位幅值。将式(6)代入式(5)得
| $ {\Pi _d} = \left( {\frac{{{\pi ^4}EI}}{{4{L^3}}} - \frac{{{\pi ^2}P}}{{4L}}} \right)v_0^2 = \frac{{{\pi ^2}P}}{{4L}}\left( {\frac{{{P_{cr}}}}{P} - 1} \right)v_0^2 $ | (7) |
式中,Pcr表示欧拉临界力。因此,外部干扰下压杆产生的广义抗力为
| $ {F_c} = - \frac{{d{\Pi _d}}}{{d{v_0}}} = \frac{{{\pi ^2}P}}{{2L}}\left( {1 - \frac{{{P_{cr}}}}{P}} \right){v_0} = - {k_{eq}}{v_0} $ | (8) |
式中,与Fc对应的虚拟弹簧常数为
| $ \overline y = \frac{{{\pi ^2}P}}{{4mgL}}\left( {\frac{{{P_{cr}}}}{P} - 1} \right){\overline x ^2} $ | (9) |
式中,坐标加上划线以示区别于压杆坐标系统。当P<Pcr时,支撑面下凹,干扰撤除后,刚球在扰动“抗力”(正弹簧力,keq>0)作用下将回到初始静平衡位置,刚球及压杆初始平衡构型是稳定的;当P>Pcr时,支撑面上凸,刚球在扰动“荷载”(负弹簧力,keq<0)作用下偏离初始静平衡位置,位移的急剧开展使其在干扰撤除后无法回到初始状态,刚球及压杆初始平衡构型是不稳定的;而当P=Pcr时,支撑面退化为平面,干扰撤除后刚球构型完全由扰动幅度决定,是不确定的,刚球及压杆处于“回归”初始构型和“新建”平衡构型间临界状态。
本节建立了理想压杆稳定性分析的等效刚球模型,在判别结构静力稳定性时,无需引入求解扰动平衡方程的静力平衡法及最小势能原理[9]等高等分析工具,便于学生和工程师理解。
二、结构静力稳定性判别的广义力增量准则对于保守系统,系统总势能与扰动下运动路径无关,式(2)和式(5)具有唯一性。非保守系统(例如承受保向力作用的压杆)的总势能与扰动过程相关,无法唯一确定[10],其稳定性分析不能采用本文提出的广义力增量准则。下面通过建立任意端部约束条件下压杆总势能[11]来推导扰动抗力Fc
| $ \begin{array}{l} \delta {\Pi _d} = EI\int_0^L {v''\left( x \right)\delta v''\left( x \right){\rm{d}}x - P\int_0^L {v'\left( x \right)\delta v'\left( x \right){\rm{d}}x} - M\delta v'\left| {_0^L - Q\delta v\left| {_0^L} \right.} \right.} \\ \;\;\;\;\;\;\; = \int_0^L {\left[ {EIv'''' + Pv''} \right]\delta v{\rm{d}}x - \left( {M - EIv''} \right)\delta v'} \left| {_0^L} \right.{\rm{ - }}\left[ {Q + EIv''' + Pv'} \right]\delta v\left| {_0^L} \right.\\ \;\;\;\;\;\;\; = \delta {\mathit{\boldsymbol{q}}^{\rm{T}}}{k_{eq}}\mathit{\boldsymbol{q}} = - \delta {\mathit{\boldsymbol{q}}^{\rm{T}}}{\mathit{\boldsymbol{F}}_c} \end{array} $ | (10) |
式中,M和Q表示压杆端部弯矩和剪力。压杆经离散化处理后,扰动位移q包含n个自由度〔采用式(6)时,n=1〕。因此,与q互为能量共轭的扰动抗力Fc变成n维向量,虚拟弹簧刚度系数keq变成n阶方阵。对实对称矩阵keq引入对角化变换keq=DTλeqD并带入式(10),得
| $ \delta {\Pi _d} = \delta {\mathit{\boldsymbol{q}}^{\rm{T}}}{k_{eq}}\mathit{\boldsymbol{q}} = \delta {\mathit{\boldsymbol{q}}^{\rm{T}}}{\mathit{\boldsymbol{D}}^{\rm{T}}}{\mathit{\boldsymbol{\lambda }}_{eq}}D\mathit{\boldsymbol{q = }}\delta {\mathit{\boldsymbol{q}}_{\bf{0}}}^{\rm{T}}{\mathit{\boldsymbol{\lambda }}_{eq}}{\mathit{\boldsymbol{q}}_{\bf{0}}} = - \delta {\mathit{\boldsymbol{q}}_{\bf{0}}}^{\rm{T}}{\mathit{\boldsymbol{F}}_{c0}} $ | (11) |
其中
| $ \begin{array}{l} {\mathit{\boldsymbol{\lambda }}_{eq}} = diag{\left[ {{\mathit{\boldsymbol{\lambda }}_1} - P{\lambda _i} - P{\mathit{\boldsymbol{\lambda }}_n} - P} \right]_{n \times n}}\\ {\mathit{\boldsymbol{q}}_0} = {\left\{ {{\mathit{\boldsymbol{q}}_{01}}\;\;{\mathit{\boldsymbol{q}}_{0i}}\;\;{\mathit{\boldsymbol{q}}_{0n}}} \right\}^{\rm{T}}} = \mathit{\boldsymbol{Dq}} \end{array} $ | (12) |
式中,λi表示keq第i个特征值。由式(11)可知,压杆广义抗力Fc0分量Fc0i形式上与式(4)和式(8)一致(均与广义扰动位移q0i成正比)。设想质量为m的刚球初始条件下位于n+1维曲面(x1, ..., xi, ..., xn, y)的坐标原点O,且广义位移q0i的基矢量为exi,曲面方程可以表示为
| $ \bar y = \sum\limits_{i = 1}^n {\frac{P}{{2mg}}\left( {\frac{{{\lambda _i}}}{P} - 1} \right)\bar x_i^2} $ | (13) |
刚球初始平衡状态的稳定性即反映了轴心压杆初始直线状态的稳定性。由上节的结论,扰动撤除后,刚球能回复到初始位置要求,式(13)中所有项恒大于零,即
| $ P < \min \left\{ {{\lambda _1}\;\;\;{\lambda _i}\;\;\;{\lambda _n}} \right\} = {\lambda _1}, $ | (14) |
由式(4)(8)(11)和(14)可知,只要确保结构在扰动下的抗力增量Fc或Fc01(与最小特征值λ1对应的广义位移q01互为能量共轭)小于零,则结构无扰平衡状态是稳定的;当Fc或Fc01恰好等于零,则结构无扰平衡状态恰好达到临界或中性平衡位置;当Fc或Fc01大于零,则结构初始平衡状态在特定扰动的影响下必然进入不稳定区域,这就是判断结构初始平衡状态稳定性的广义力增量准则。考虑到广义力做功转化为结构总势能,此准则为多自由度系统线性稳定性分析的能量方法提供清晰的物理解释。
三、结语为了避免柔性结构因稳定极限承载力过早耗尽而被破坏,工程师必须充分理解结构受载状态稳定性的物理概念和判别方法。本文基于经典弹性稳定理论关于平衡状态稳定性判别的刚球模型,通过扰动广义抗力分析,揭示刚球与理想压杆扰动抗力形成的共性机理,建立理想压杆稳定性分析的等效刚球模型,在此基础上提出结构静力稳定性判别的广义力增量准则。旨在让学生充分认识结构变形抗力决定其在干扰撤除后回复到无扰平衡状态的能力,从而建立复杂结构在任意约束和荷载条件下平衡状态稳定性的物理概念。
值得注意的是,本文建立的寻找结构失稳临界状态或中性平衡的标准(广义力增量为零)仅适用于线性稳定分析。对于结构非线性稳定问题,尽管无法直接算出失稳临界荷载(必须考虑变形过程的影响),但可以通过非线性有限元分析逐步计算结构当前受力状态,利用广义力增量准则可判断结构是否稳定,从而成功预测下一步结构的变形路径(后屈曲分析)。
| [1] |
陈绍蕃. 钢结构设计原理[M]. 4版. 北京: 科学出版社, 2015.
|
| [2] |
Chen W.F., Lui E.M. Structural Stability-Theory and Implementation[M]. New Jersey: Prentice Hall, Upper Saddle Rive, 1987.
|
| [3] |
任伟新. 结构稳定性概念的引入和阐明[J]. 长沙铁道学院学报, 1991(2): 23-28. |
| [4] |
郭小农, 秦朗, 黄玮嘉, 等. 钢梁整体稳定教学实验装置改进设计[J]. 高等建筑教育, 2015, 24(1): 123-126. |
| [5] |
李贤, 丁北斗, 张营营. 钢结构轴心压杆稳定性教学中ANSYS软件的应用[J]. 高等建筑教育, 2016, 25(2): 162-166. |
| [6] |
崔文一. 钢结构基本原理和材料力学原理教学的对比研究[J]. 高等建筑教育, 2014, 23(5): 63-65. |
| [7] |
Ziegler H. Principles of Structural Stability[M]. Massachusetts: Blaisdell Publishing Company, 1968.
|
| [8] |
周绪红. 结构稳定理论[M]. 北京: 高等教育出版社, 2010.
|
| [9] |
陈骥. 钢结构稳定理论与设计[M]. 6版. 北京: 科学出版社, 2014.
|
| [10] |
Timoshenko S.P., Gere J.M.. Theory of Elastic Stability, Second Edition[M]. New York: McGraw-Hill Book Company Inc., 1961.
|
| [11] |
曾庆元, 周智辉, 文颖. 结构动力学讲义[M]. 北京: 人民交通出版股份有限公司, 2015.
|
 2019, Vol. 28
2019, Vol. 28

