b. 武汉理工大学设计研究院有限公司, 湖北 武汉 430070
b. Design & Research Institution Co., Ltd., Wuhan University of Technology, Wuhan 430070, P. R. China
钢结构课程教学过程中,稳定问题是学生学习钢构件设计知识的重点和难点,压弯钢构件整体稳定问题尤其如此。压弯构件可能在弯矩作用平面内弯曲失稳,也可能在弯矩作用平面外弯扭失稳,这两种失稳形式的性质不同,应分别计算[1]。压弯构件弯矩作用平面内与平面外稳定实用计算公式的构建过程,涉及失稳现象的概念、失稳准则的应用,以及公式构建的理论方法和处理技巧,学习有一定的难度。作为钢结构课程教师应结合稳定问题的教学,引导学生认识问题的现象,探究问题的本质和问题的求解方法,让学生能在专业课程学习中重视公式的演绎过程,掌握公式的推演依据和相关理论,掌握解决稳定问题的思维方式,学习解决科学研究问题的方法,认识力学知识在结构工程专业知识学习中的重要性。
一、失稳现象的描述构件在轴心压力和弯矩的共同作用下产生弯矩作用平面内的弯曲变形,当荷载达到一定值时,材料屈服进入弹塑性受力状态,随截面塑性区扩展构件产生较大挠度,进而达到极限状态不能维持稳定平衡, 发生弯曲失稳,变形仅限于平面,此为压弯构件弯矩作用平面内的失稳现象。压弯构件的平面内整体失稳属于极值点失稳问题[2]。
构件在轴心压力和弯矩的共同作用下,当荷载未达到某一限值时,构件会始终保持稳定的平衡状态,此时只在弯矩作用平面内出现小挠度。若弯矩作用平面外没有足够支撑,一旦荷载达到某一数值时,在弯矩作用平面外呈现小挠度变形,同时截面产生扭转,即发生弯扭失稳,变形不再仅限于平面,而延伸到空间,此为压弯构件弯矩作用平面外的失稳现象。压弯构件的平面外整体失稳属于分岔失稳问题[3]。
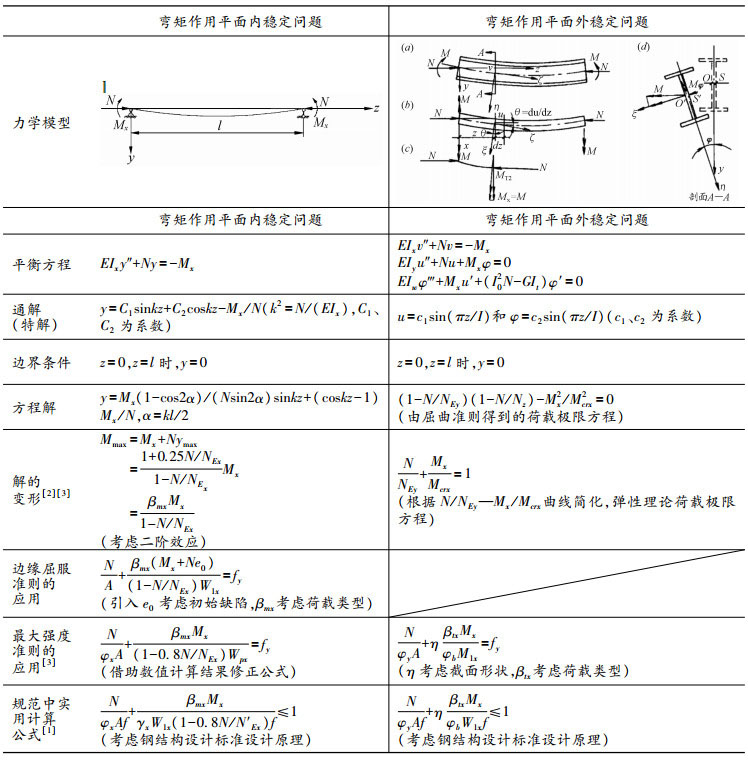
二、力学模型弯矩作用平面内稳定问题的力学模型:首先视压弯构件为一根弹性杆件,两端简支并承受轴心压力和弯矩的共同作用,仅产生弯矩作用平面内的挠度变形。为准确计算构件的最大弯矩,要考虑轴力在最大挠度值处产生的二阶效应;由于实际工程中钢构件的制作工艺等因素,要考虑其初始缺陷;为充分发挥材料性能,计算中也要考虑材料弹塑性的影响。
弯矩作用平面外稳定问题的力学模型:构件的受力和支座形式与平面内稳定问题相同,但由于侧向没有足够的支撑,所以产生的变形不仅包括弯矩作用平面内的挠度变形,而且产生了弯矩作用平面外的挠度变形和截面扭转角。由于构件截面变形形式的复杂性,首先用平衡法推导公式时做以下假设:构件为无缺陷的弹性体;发生弯曲与扭转变形时,变形都是微小的,且截面形状不变;在弯矩作用平面内的抗弯刚度很大,平面内的弯曲变形对弯扭屈曲的影响不考虑[4]。其次再考虑实际工程构件的初始缺陷、几何非线性以及材料的非线性等因素的影响。最后再对弹性理论演绎的公式进行修正。
三、失稳准则失稳准则的正确选用关系到各类稳定问题的正确求解,钢构件稳定问题常用的三大稳定判断依据:屈曲准则、边缘屈服准则、最大强度准则。构件不同的失稳问题,应选用不同的失稳准则。由于问题求解的复杂性,往往需要联合应用多个准则。压弯构件弯矩作用平面内稳定计算公式的推导中用到了边缘屈服准则和最大强度准则,压弯构件弯矩作用平面外稳定计算公式的推导中用到了屈曲准则和最大强度准则。这在后面公式构建理论中将给出明确的理由。
四、公式构建理论压弯构件弯矩作用平面内和平面外稳定问题的求解理论和推演过程一般采用对比方式教学。表 1给出了双轴对称截面压弯构件的两类稳定问题求解方法的对比。
| 表 1 整体稳定公式推演过程对比 |
表 1中符号说明:N、Mx分别为构件承受的轴力和绕x轴弯矩;E、G分别为材料弹性模量、剪切模量;Ix、Iy、Iw分别为截面对x、y、z轴惯性矩;It为截面的抗扭惯性矩;NEx、NEy、Nz、Mcrx分别为杆件绕x、y轴弯曲失稳欧拉临界力,绕z轴扭转失稳欧拉临界力和绕x轴临界弯矩,e0为等效偏心距,İ0为截面对剪心的极回转半径,A为杆件截面面积,W1x为最大受压纤维的毛截面模量;φx、φy分别为弯矩作用平面内和平面外的轴心受压杆件稳定系数,φb为均匀弯曲梁的整体稳定系数;fy为材料屈服强度,γx为塑性发展系数,N′Ex为欧拉临界力NEx除以抗力分项系数γR,N′Ex=NEx/γR, βmx、βtx分别弯矩作用平面内问题和弯矩作用平面外问题的等效弯矩系数,η为截面型式调整系数。
表 1所示,对于弯矩作用平面内失稳,首先对初始的力学模型列出平衡方程。方程中自由度只有一个平面内挠度y,得到关于y、z的二阶常系数线性微分方程;根据支座的边界条件进行求解,得出跨中最大挠度;根据二阶弹性分析计算构件的最大弯矩Mmax,借助边缘屈服准则得到基础公式,公式中引进等效偏心距e0来考虑构件初始缺陷的影响,βmx考虑荷载弯矩等效。边缘屈服准则没有考虑材料的塑性发展,与实际情况有一定的差异,用此理论偏于保守,对工程设计而言也不经济。为此进一步考虑材料的弹塑性工作性能,对借助弹塑性理论数值计算的结果进行对比分析,对边缘屈服准则进行修正,得到满足最大强度准则的平面内稳定问题的理论公式。公式中φx反映了最大强度准则的应用,而系数0.8是参照大量的数值模拟结果对边缘屈服准则公式的修正。依据现行钢结构设计原理,引进截面塑性发展系数γx来考虑截面塑性发展,将Wpx用γxW1x代替;将NEx除以抗力分项系数,用N′Ex代替,用材料强度的设计值f代替屈服强度fy,最终得到其实用计算公式。
表 1所示,对于弯矩作用平面外失稳,首先对初始的力学模型列出平衡方程,其自由度有平面内挠度v、平面外的挠度u和扭转角φ共三个。关于v的弯矩平衡方程是独立的,已在弯矩作用平面内稳定问题中求解;关于u、φ构建的两个平衡方程是平面外的挠度和扭转角的耦合方程,根据支座的边界条件和屈曲准则得到弹性理论的荷载极限方程式[5]。再利用数学简化,并出于对结构稳定安全的保证,得出表中所示荷载极限方程式。理论分析和实验研究表明,其形式同样适用于弹塑性压弯构件的弯扭屈曲计算[3]。因此如同平面内稳定问题一样,考虑材料弹塑性、构件的初始缺陷、荷载类型以及截面的开口闭口形状,为此在弹性极限方程的基础上,引进等效弯矩系数βtx、截面调整系数η,并应用NEy=φyAfy,Mcrx=φbW1xfy,得到弯矩作用平面外稳定问题满足最大强度准则的理论计算公式。依据现行钢结构设计原理,用材料强度设计值f代替屈服强度fy,得到压弯构件弯矩作用平面外稳定计算的实用公式。
表 1以对比方式展示了两类稳定问题的求解理论和求解途径,学生通过对比学习,从中能很好地体会两类稳定问题的异同点。
五、结语通过从失稳现象的描述、力学模型的建立、失稳准则的选用和公式的构建等几个方面的对比,详细解析了压弯构件弯矩作用平面内与弯矩作用平面外稳定问题包含的力学问题及其解决方法,如:二阶效应、弹塑性理论、材料缺陷、简单理论到复杂理论的过渡以及理论的合理修正等,将稳定问题的求解过程完整表现出来。这样不仅能使学生深入理解压弯构件的整体稳定问题,以及问题求解涉及的重要力学知识,并且能有效地引导学生重视公式的演绎过程,掌握公式的推演依据和相关理论,培养学生对工程中力学问题的深入思考能力。
| [1] |
中华人民共和国国家标准.钢结构设计标准(GB 50017-2017)[S].北京: 中国计划出版社, 2017.
|
| [2] |
陈军明, 雷航. 弯矩作用平面内稳定公式推导的力学问题[J]. 力学与实践, 2013, 35(4): 66-67. |
| [3] |
戴国欣. 钢结构[M]. 4版. 武汉: 武汉理工大学出版社, 2012.
|
| [4] |
陈骥. 钢结构稳定理论与设计[M]. 5版. 北京: 科学出版社, 2011.
|
| [5] |
沈祖炎, 陈扬骥, 陈以一. 钢结构基本原理[M]. 北京: 中国建筑工业出版社, 2005.
|
 2019, Vol. 28
2019, Vol. 28