课程设计是土木工程专业极其重要的实践环节,是指导学生将刚学完的单门课程进行一次实践的过程,其主要作用是强化学生对基本理论知识的理解和运用。钢结构课程设计是土木工程专业十分重要的一门实践课程,通过钢结构课程设计,可以加深学生对钢结构课程知识的理解,熟悉钢结构设计过程,锻炼学生利用手册、规范等工具书的能力,培养学生综合分析问题和运用钢结构基础理论知识解决实际工程问题的能力,为毕业设计打下坚实的基础,也有助于学生毕业后能尽早进入工作角色。扎实有效地开展钢结构课程设计,为培养应用型专业技术人才奠定基础,有着理论课教学无法替代的作用[1-3]。
钢结构课程设计成绩是对学生课程设计效果的最终评价。由于课程设计这种实践类课程不像笔试考试那样有标准答案或参考答案,每题有具体的评分标准,所以钢结构课程设计成绩的评定具有一定的人为性、随意性和模糊性。传统钢结构课程设计成绩的评定,通常是教师根据学生平时表现、设计说明书及施工图纸质量、课程设计答辩情况等因素,综合考虑后定性地给个分数[4-6]。许多教师意识到这种方法的不合理性,会提前制定考核办法,事先给出各个因素所占的权重值,然后根据每项的分数,结合事先确定的各因素权重值进行计算,得出最终成绩。如武汉工程大学钢结构课程设计成绩评定方法如表 1所示。
| 表 1 钢结构课程设计成绩评定方法 |
钢结构课程设计传统的成绩评定方法很难全面合理、科学地反映学生的综合水平。在组织纪律方面一般仅根据考勤情况最后给学生一个成绩,而忽视了学生的课堂纪律,以及每天是否按教师要求完成了学习任务;对学生的学习态度也较难掌握,一般只是根据学生平时表现来评定;设计说明书和施工图是课程设计的最终成果,传统评价方法一般是教师审阅后根据自己的印象适当给分;答辩情况也是根据学生的表现,教师凭自己的印象给分,人为主观因素影响很大,成绩评定极不合理,也不科学。因此,为减少主观因素的影响,建立一种科学、合理、定量和客观的钢结构课程设计成绩评定方法是非常必要的。公平、公开、全面、合理的成绩评价方法不仅有利于调动学生的积极性、主动性,而且也有利于提高课程的质量[7-10]。
层次分析法是一种定性分析与定量分析相结合的系统分析方法,是将人的主观判断用数学形式表达和处理的方法,也称AHP(Analytic Hierarchy Process)法[11]。本文探讨运用层次分析法对学生钢结构课程设计成绩的评定。
一、建立成绩评价指标体系传统的钢结构课程设计,一般要求学生在一周或者两周时间内完成一榀普通钢屋架的设计,涉及的内容有:荷载统计计算、构件及节点设计、内力分析和绘制钢结构施工图等。根据钢结构课程设计的特点,主要考虑从以下5个方面进行考核,即:组织纪律、学习态度、设计说明书质量、施工图质量和答辩情况。可以将上述5个影响最终成绩的因素作为一级评价指标,将钢结构课程设计成绩评定作为最高目标层[4-5, 10]。
(一)组织纪律为保证学生在规定的时间内完成课程设计任务,应对学生进行考勤。和理论课要求一样,有事要事先请假,不能无故缺课,不能迟到早退。良好的组织纪律是顺利完成课程设计任务的前提,否则根本无法保证课程设计的质量。因此,确定组织纪律下的二级评价指标层为:出勤率、遵守纪律和按时完成各阶段任务(进度要求)。
(二)学习态度同样的任务,通常学习态度端正的学生完成的质量要好一些,积极主动学习的学生解决问题的综合能力要高于消极被动学习的学生。有些学生吃苦耐劳,虚心学习,能发现问题、提出问题和解决问题,独立完成任务,达到教学目的;有些学生则需要借鉴其他学生的成果,模仿着解决问题;有些学生虽然每天都在教室内,但学习进度慢,有的最后还抄袭他人的成果,草草完成任务。因此,指导教师在课程设计过程中要随时掌握学生的学习态度。据此,确定学习态度下的二级评价指标为:独立性、主动性和积极性。
(三)设计说明书质量钢结构课程设计最终的成果主要是设计说明书和施工图,设计说明书的质量在最终成绩评定中具有举足轻重的地位。设计说明书的质量主要包括以下一些内容:概念是否清晰,计算是否正确,内容是否完整,层次是否分明,条理是否清晰,文字表达是否流畅。因此,一级评价指标设计说明书质量下的二级评价指标确定为:内容完整、计算正确、条理清晰、文字表达流畅。
(四)施工图质量工程图是工程师的语言,绘图是工程设计乃至整个工程建设的一个重要环节。施工图的质量和设计说明书质量一样,在最终成绩评定中具有相同的地位。施工图质量主要包括图面整洁性、制图规范性、内容完整性、尺寸标注全面性等。据此,确定施工图质量下的二级评价指标为:图面整洁、标注齐全、制图规范、内容完整。
(五)答辩情况课程设计完成后,由2~3名教师负责课程答辩,可以有效调动学生的学习积极性。通过答辩环节,指导教师能进一步了解学生设计的真实水平。课程答辩情况一般包括自述表达情况、个人应变能力情况、回答问题的完整性、准确性等。因此,确定答辩情况下的二级评价指标为:自述表达情况、个人应变能力和回答问题完整准确。
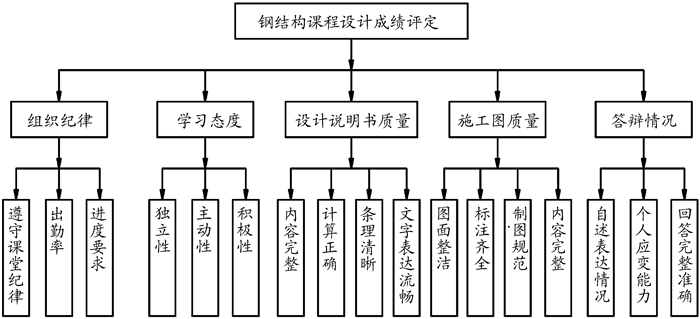
(六)最终成绩评价指标体系根据上述分析,将钢结构课程设计成绩评定体系分为3个层次,第一层中一个元素,即钢结构课程设计成绩评定,该层是最高层,也是目标层。第二层为中间层,这一层次主要包括要实现最高层目标所涉及中间环节需要考虑的各种影响因素,包括上述5个影响因素。第三层为最底层,通过上述5个影响因素的分析,提出各自二级指标层,共17个。因此,钢结构课程设计成绩评定体系的层次结构如图 1所示。
|
图 1 钢结构课程设计成绩评定体系的层次结构图 |
钢结构课程设计成绩评定体系的各层评价因子确定之后,各因素对最高目标层有着不同的影响程度。因此,还需要确定各个因素所占的权值,即权重系数,它是表示因素重要性的一个相对数字。运用层次分析法计算权值的基本方法及步骤如下。
1.构造判断矩阵
用Ui(i=1,2,3……)表示参评同层次间的各个因素,Uij表示Ui对Uj(j=l,2,3……)相对重要性的数值,取值依据表 2。
| 表 2 判断矩阵标度及其含义 |
用A表示目标判断矩阵,则有n个影响因素,A即构成n阶矩阵。
2.重要性排序
根据判断矩阵,求出判断矩阵的最大特征值所对应的特征向量,该特征向量即为各评价因素重要性排序,即为权重系数。
3.权值合理性检验
权值的合理性采用公式(1)进行检验。
| $ \mathrm{C}_{\mathrm{R}}=\frac{\mathrm{C}_{\mathrm{i}}}{\mathrm{R}_{\mathrm{i}}} $ | (1) |
式中:Ci为判断矩阵的一般一致性指标,由公式
| 表 3 1~9阶矩阵Ri取值表 |
层次分析法认为,当CR<0.10时,可以认为判断矩阵具有满意的一致性,说明权值数分配是合理的。其中,1阶和2阶判断矩阵具有完全一致性,Ri = 0,不需进行权值合理性检验[12]。
(二)第二层权重系数确定1.构造判断矩阵
以钢结构课程设计成绩评定作为目标,根据图 1中第二层次5个影响因素之间的相互比较,构成判断矩阵如表 4所示。
| 表 4 第二层权重矩阵表 |
2.计算权重系数
采用和法(公式2)求取该判断矩阵的特征值和特征向量,即:将判断矩阵(记为A)按列归一化后各行相加,相加后的向量除以n(该处n=5),即得权重向量。具体计算步骤如下。
| $ {\omega _i} = \frac{{\sum\limits_{j = 1}^n {{a_{ij}}} }}{{n\sum\limits_{k = 1}^n {\sum\limits_{j = 1}^n {{a_{kj}}} } }}\quad {\rm{i}} = 1, 2, 3 \cdots \cdots $ | (2) |
根据表 4得到判断矩阵A如下:
| $ A=\left(\begin{array}{ccccc} {1} & {\frac{1}{2}} & {\frac{1}{4}} & {\frac{1}{4}} & {\frac{1}{2}} \\ {2} & {1} & {\frac{1}{3}} & {\frac{1}{3}} & {\frac{1}{2}} \\ {4} & {3} & {1} & {1} & {3} \\ {4} & {3} & {1} & {1} & {3} \\ {2} & {2} & {\frac{1}{3}} & {\frac{1}{3}} & {1} \end{array}\right) $ |
对矩阵A按列进行归一化得到如下矩阵:
| $ \left(\begin{array}{ccccc} {0.08} & {0.06} & {0.10} & {0.10} & {0.07} \\ {0.15} & {0.11} & {0.11} & {0.111} & {0.07} \\ {0.31} & {0.32} & {0.34} & {0.34} & {0.37} \\ {0.31} & {0.32} & {0.34} & {0.34} & {0.37} \\ {0.15} & {0.21} & {0.11} & {0.11} & {0.12} \end{array}\right) $ |
对该矩阵行向量求和后取平均值,得到判断矩阵特征向量为:
| $ \omega = {(0.08\quad 0.111\quad 0.34\quad 0.34\quad 0.13)^{\rm{T}}} $ |
因此,该特征向量即为各评价因素的权重系数。
3.权值合理性检验
由上述矩阵A和特征向量ω,可以按以下公式(3)计算矩阵的特征值λ。权值的合理性检验按公式(1)进行。
| $ \lambda \omega=\mathrm{A} \omega $ | (3) |
即:
因,
所以,
| $ \lambda=\frac{1}{5}\left(\frac{0.37}{0.08}+\frac{0.56}{0.11}+\frac{1.72}{0.34}+\frac{1.72}{0.34}+\frac{0.74}{0.13}\right)=5.1 $ |
因此,判断矩阵A的一般一致性指标为:
| $ {{\rm{C}}_{\rm{i}}} = \frac{{\left( {{\lambda _{\max }} - n} \right)}}{{(n - 1)}} = \frac{{5.1 - 5}}{{5 - 1}} = 0.025 $ |
按n=5,查表 3,可得Ri=1.12。
代入公式(1)检验权值合理性,
| $ \mathrm{C}_{\mathrm{R}}=\frac{\mathrm{C}_{\mathrm{i}}}{\mathrm{R}_{\mathrm{i}}}=\frac{0.025}{1.12}=0.022 <0.10 $ |
故,判断矩阵具有满意的一致性。
(三)第三层各影响因素的权值计算按照上述方法对第二层次5个影响因素下的第三层次各因素进行两两对比,构建相应的判断矩阵,求取各自对应的特征向量,可以得到第三层次17个评价因子的各自权重系数。
通过层次分析法计算,得出钢结构课程设计成绩评定体系各评价因子权值见表 5。
| 表 5 钢结构课程设计成绩评定体系各因子权重系数 |
学生钢结构课程设计成绩最后是按照百分制确定的。通过上述层次分析法只是确定了各层指标的权值系数,没有具体的成绩。为合理确定每个学生的成绩,需要教师在平时指导学生的整个过程中,对底层(第三层)指标按百分制进行打分,然后乘以相应的权值系数得到学生最终成绩。
对底层指标的相应分数,每个教师可根据实际情况制定相应的评分标准,再根据评分标准制作学生的底层指标评分表,作为学生最后完成课程设计的底层指标相应的百分制成绩。表 6为钢结构课程设计底层指标成绩评定的参考方法,主要是以100分为各底层指标对应的基本分,然后在此基础上根据学生表现进行相应扣分。
| 表 6 钢结构课程设计底层指标成绩评定参考方法 |
指导教师可以根据第三层次的17个指标,对每个学生17个方面的表现按百分制进行打分,最后按照公式(4)和公式(5)计算学生的最终得分,用F表示。
| $ F = \sum\limits_{i = 1}^5 {{a_i}} {E_n} $ | (4) |
| $ {E_n} = \sum\limits_{j = 1}^n {{b_j}} {f_j} $ | (5) |
式中,F为学生最终得分;ai为一级指标层的权重系数;En表示第二层指标(评价体系中的中间层)中各项所得总分;bj表示二级评价因子的权重系数;fj表示第三层(评价体系中的最底层)各指标平时按百分制打分所得的分值。
五、实例应用分析钢结构课程设计一般安排在大学第6个学期(大三下学期)期末进行。以下以武汉工程大学2015级土木工程专业某学生钢结构课程设计成绩评定为例,说明如何运用层次分析法获得其最终成绩。根据该学生平时表现、完成的成果及答辩情况,指导教师绘制成绩评定表格,对其第三层次17个指标分别打分,该学生各项成绩如表 7所示。
| 表 7 2015级某学生各评价指标分数一览表 |
用表 5中的权值系数乘以各项得分得到第二层指标(评价体系中的中间层)中各项所得总分(表 6),按照该成绩评定方法,该生最终成绩F为:F=0.08×92.06+0.11×91.65+0.34×88.88+0.34×90.82+0.13×88.95=90.11。
这种成绩评定方法手工计算量较大,容易出错,可以在Excel中嵌套公式计算,只需要把学生第三层17项指标原始考核分数输入就可以计算出学生的最终成绩。
运用新的成绩评定方法之后,学生的学习状况有了根本的转变。学生基本上都能按时到达指定教室,认真作业,积极思考和提问的学生比以往明显增多,学习的积极性和主动性也有提高。该届大部分学生都提前完成了课程设计任务,最终的设计说明书和施工图质量也有了较大的提高,平均分比以往几届高出5分左右。可见,新的钢结构课程设计成绩评定方法促进了课程设计质量的提高。
六、结语钢结构课程设计是土木工程专业一门重要的实践课程,传统的钢结构课程设计成绩评定方法存在考核不客观,较难真实反映学生综合水平的弊端。本文探讨并提出基于层次分析法的钢结构课程设计成绩计算方法,使课程考核更为科学、合理。
通过分析影响钢结构课程设计成绩的影响因素,建立5个一级评价指标和17个二级评价指标,运用层次分析法建立钢结构课程设计成绩评定模型。实践证明,基于层次分析法的钢结构课程设计成绩评定方法减少了主观因素的影响,能充分激发学生学习的积极性、主动性,提高课程设计的质量。
| [1] |
王秀丽. 钢结构课程设计指南[M]. 北京: 中国建筑工业出版社, 2010.
|
| [2] |
张志国, 张庆芳. 钢结构课程设计指导[M]. 武汉: 武汉理工大学出版社, 2010.
|
| [3] |
丁家玲, 叶金华. 层次分析法和模糊综合评判在教师课堂教学质量评价中的应用[J]. 武汉大学学报:哲学社会科学版, 2003, 56(2): 241-245. |
| [4] |
蒋德稳, 张三柱. 对《钢结构课程设计》的几点思考[J]. 皖西学院学报, 2006, 22(5): 135-137. DOI:10.3969/j.issn.1009-9735.2006.05.039 |
| [5] |
孙德发, 李刚, 刘俊英. 关于提高钢结构课程设计教学质量的教改实践[J]. 嘉兴学院学报, 2008, 20(5): 139-141. DOI:10.3969/j.issn.1008-6781.2008.05.034 |
| [6] |
陈新, 李德建, 冯吉利. 钢结构系列课程教学内容改革思考[J]. 高等建筑教育, 2010, 19(4): 63-67. |
| [7] |
陈俊岭, 焦燏烽. 钢结构课程设计教学方法探讨[J]. 高等建筑教育, 2012, 21(5): 108-110. |
| [8] |
董晓马. 基于模糊数学的土力学实验成绩评定[J]. 实验室科学, 2015, 18(2): 219-221. DOI:10.3969/j.issn.1672-4305.2015.02.066 |
| [9] |
余卫华, 王正中, 蔡坤. 钢结构课程设计教学改革与实践[J]. 高等建筑教育, 2015, 24(1): 69-71. |
| [10] |
郇筱林, 戴素娟. 土木工程专业钢结构课程设计质量监控体系的构建[J]. 高等建筑教育, 2015, 24(5): 103-105. |
| [11] |
T.L.萨蒂.层次分析法——在资源分配管理和冲突分析的作用[M].许树柏, 等译.北京: 煤炭工业出版社, 1988.
|
| [12] |
王亚军. 河北涞源矿山地质环境影响程度综合评价[J]. 矿产勘查, 2010, 1(6): 586-591. DOI:10.3969/j.issn.1674-7801.2010.06.019 |
 2019, Vol. 28
2019, Vol. 28

