材料力学课程是工程类本科专业的重要专业基础课,对后续课程的学习和工程应用都有重要意义。多年来,我国材料力学课程教材建设在引进和吸收国外教学资源的基础上,建立了适合国情的比较完善的材料力学课程教材体系,孙训方[1]、刘鸿文[2]、叶开沅[3]、苏翼林[4]和单辉祖[5]等在这方面进行了长期的探索并作出杰出的贡献。在材料力学课程教材体系的创新和改革方面也有许多学者进行了积极的探索,如范钦珊等[6-7]把超静定部分独立成章,增加新材料的章节,并引入材料力学计算机辅助分析等内容。黄小清等[8]则把内力分析独立成章,对教材作了进一步完善。总的来说,我国材料力学课程教材建设取得了许多成绩,为高等教育事业和工程技术人才培养作出了重要贡献。但国内现行材料力学课程教材有关梁截面形状对梁弯曲弯曲正应力强度的影响、工字型截面梁截面上最大切应力计算等内容普遍存在概念不清的问题,对教师的讲授和学生的学习带来一定困扰,不利于材料力学课程教学和学生对课程知识的掌握。
本文根据材料力学基本原理对上述问题进行了详细分析,厘清了一些模糊概念,为材料力学课程教学和教材的完善提供参考。同时, 该研究过程和研究方法也为提高学生的科学素养和培养学生的科学研究能力提供了一个较好的案例。
一、梁截面形状对梁弯曲正应力强度的影响国内现行材料力学课程教材,大都定义单位面积的弯曲截面系数来说明截面形状对梁弯曲正应力强度的影响,并认为工字型截面弯曲正应力强度最好,矩形截面次之,圆形截面最差。如刘鸿文[2]教材(166页)、黄小清[8]教材(156页)、杨伯源[9]教材(152页)、赵九江等[10]教材(125页)、黄世伟等[11]教材(106页)、古滨[12]教材(138页)、戴宏亮[13]教材(110页)、王国超[14]教材(129页)和冯晓九[15]教材(117页)都有这种表述。还有许多材料力学课程教材也有类似结论,这里不再一一引述。实际上,这种表述忽略了矩形截面宽高比变化、工字型截面宽高比和腹板宽高比变化对弯曲正应力强度的影响,所以是不准确的。黄超等[16]教材(145页)指出矩形截面高宽比大于0.716时,其弯曲正应力强度才大于圆形截面梁,该结论是正确的,但该教材没有给出工字型截面高宽比变化对梁强度的影响规律。
教学中,如果学生接受了“工字型截面弯曲正应力强度最好,矩形截面次之,圆形截面最差”的结论,则会在思维上形成惯性。一旦学生走出校门参与工程设计和应用,会忽略具体情况,产生错误的设计产品以及使用错误的工程制造、监控方法,严重时可能造成安全隐患和事故。另外,如果材料力学课程教材在描述强度问题上存在错误,对培养学生严谨的学风、正确的科学思想和掌握科学研究方法产生非常不利的影响。所以,作为重要的工程应用专业基础课,必须讲清楚截面不同形态对梁弯曲正应力强度影响的问题。
下面分别讨论相同面积条件下矩形截面与圆形截面梁,以及矩形截面与工字型截面梁的弯曲正应力强度之比与截面尺寸参数的关系。
考虑宽为B、高为H的矩形截面并设γ=B/H,表示截面的宽高比即竖放程度,γ越小竖放程度越大。再考虑另一直径为D的圆形截面,设两者面积相等,则有
| $ g(\gamma ) = \frac{{B{H^2}}}{6} \times \frac{{32}}{{\pi {D^3}}} = \frac{2}{3}\sqrt {\frac{\pi }{\gamma }} $ | (1) |
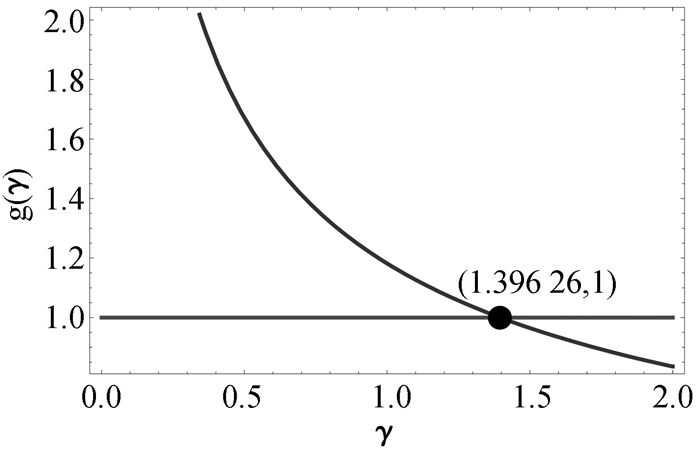
当γ=1.396 26时,g(γ)=1,矩形截面和圆形截面梁的弯曲正应力强度相同,与黄超等[16]的结论一致。当γ≠1.396 26,g(γ)随γ的变化关系如图 1所示。
|
图 1 g(γ)随γ的变化关系 |
从图 1可知,γ>1.396 26时,矩形截面属横放状态,其弯曲正应力强度小于圆形截面;γ < 1.396 26时,矩形截面包括竖放和横放两种状态,其中γ < 1的部分属竖放状态,1 < γ < 1.396 26的部分属横放状态,其弯曲正应力强度均大于圆形截面。可见,矩形截面梁弯曲正应力强度是否优于圆形截面梁,取决于其宽高比。
算例1,设圆形截面的直径为D=30.403 5 mm,矩形截面的宽高分别为B=33 mm, H=22 mm, 则两者面积相等,且矩形的宽高比γ=1.5。此时矩形截面和圆形截面的弯曲截面系数分别为Wjz=2 661.08 mm3和Wyz=2 758.17 mm3。可见此时矩形截面的弯曲正应力强度小于圆型截面的弯曲正应力强度。
算例2,设圆的直径为D=30.901 9 mm,矩形的宽高分别为B=30 mm, H=25 mm, 则两者面积也相等,且矩形的宽高比γ=1.2。此时矩形截面和圆形截面的弯曲截面系数分别为Wjz=3 125 mm3和Wyz=2 896.51 mm3。可见此时矩形截面的弯曲正应力强度大于圆型截面的弯曲正应力强度。
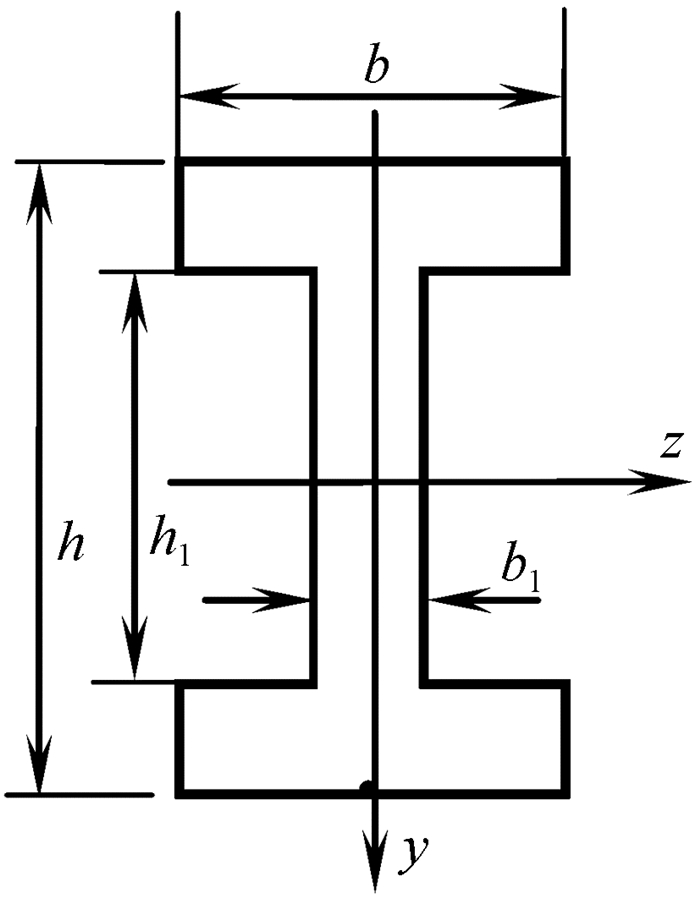
再考虑矩形截面和工字型截面梁的弯曲正应力强度之比,工字型截面尺寸如图 2所示。设α=h1/h, β=b1/b, λ=b/h,λ表示截面的竖放程度,λ越小竖放程度越大。由工字型与矩形截面的面积相等,可得
| $ H = \frac{{\sqrt {\lambda [(1 - \alpha ) + \alpha \beta ]} }}{{\sqrt \gamma }}h $ | (2) |
|
图 2 工字型截面 |
工字型截面的弯曲截面系数可表示为
| $ {W_{gz}} = \frac{1}{6}\lambda {h^3}\left[ {1 + {\alpha ^3}(\beta - 1)} \right] $ | (3) |
因此,可得矩形截面与工字型截面的弯曲正应力强度之比为
| $ f(\alpha , \beta , \lambda , \gamma ) = \frac{{B{H^2}}}{{6{W_{gz}}}} = \frac{{{{[1 + \alpha (\beta - 1)]}^{3/2}}}}{{\left[ {1 + {\alpha ^3}(\beta - 1)} \right]}}\sqrt {\frac{\lambda }{\gamma }} = q(\alpha , \beta )\sqrt {\lambda /\gamma } $ | (4) |
其中
| $ q(\alpha , \beta ) = \frac{{{{[1 + \alpha (\beta - 1)]}^{3/2}}}}{{\left[ {1 + {\alpha ^3}(\beta - 1)} \right]}} $ | (5) |
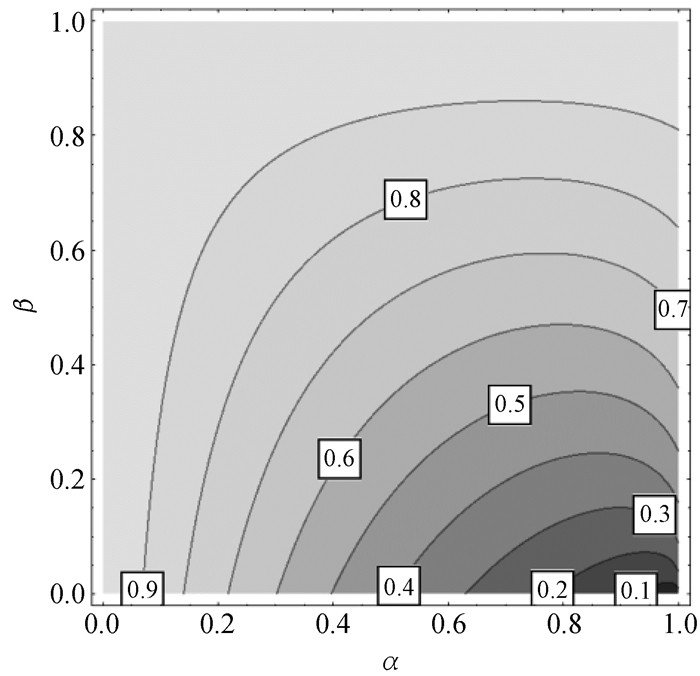
从式(4)知,矩形截面与工字型截面的弯曲正应力强度之比与
|
图 3 q(α, β)的等高线 |
在α很小或β很大,即腹板很矮或腹板很宽时,q(α, β)接近于1,此时,若工字型截面的竖放程度小于矩形截面的竖放程度,即
| $ {f_1}(\alpha , \beta ) = \frac{{\sqrt {42} {{[(1 - \alpha ) + \alpha \beta ]}^{3/2}}}}{{6\left[ {1 + {\alpha ^3}(\beta - 1)} \right]}} $ | (6) |
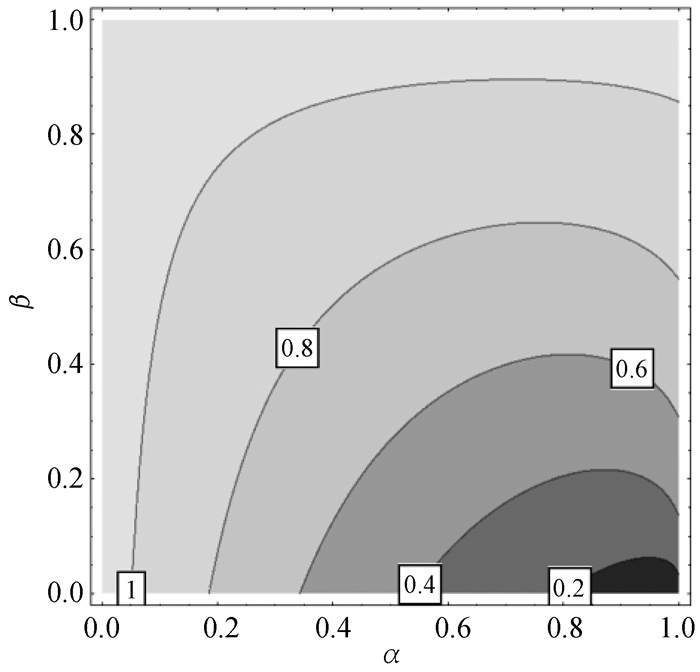
式(6)的等高线,如图 4所示
|
图 4 f1(α, β)的等高线 |
由图 4可见,此时存在矩形截面的弯曲正应力强度大于工字型截面的弯曲正应力强度的可能。判断条件是f1(α, β)>1,对应于图 4上等高值为1的等高线以外的尺寸参数区域, 即腹板很矮或腹板很宽的情形。
当工字型截面的竖放程度大于或等于矩形截面的竖放程度,即
算例3.设矩形的宽高分别为B=127 mm, H=211.66 mm, 工字型截面的尺寸分别为b=140 mm, h=200 mm,b1=112 mm, h1=40 mm。则α=0.2,β=0.8,λ=0.7,γ=0.6。此时,两者面积相等,工字型截面腹板很矮,工字型截面的竖放程度小于矩形截面的竖放程度。通过计算可得此时矩形截面和工字型截面的弯曲截面系数分别为Wjz=0.95×106 mm3和Wgz=0.93×106 mm3,即矩形截面的弯曲正应力强度大于工字型截面的弯曲正应力强度。根据式(6)可知,此时也有f1(α, β)=1.0176>1,所以前面的结论是正确的。
算例4.设矩形的宽高分别为B=124.32 mm, H=207.20 mm, 工字型截面的尺寸分别为b=140 mm, h=200 mm,b1=126 mm, h1=160 mm。则α=0.8,β=0.9,λ=0.7,γ=0.6。此时,两者面积也相等,工字型截面腹板很宽,工字型截面的竖放程度小于矩形截面的竖放程度。通过计算可得此时矩形截面和工字型截面的弯曲截面系数分别为Wjz=0.89×106 mm3和Wgz=0.88×106 mm3,即矩形截面的弯曲正应力强度大于工字型截面的弯曲正应力强度。根据式(6)可知,此时也有f1(α, β)=1.004 6>1,所以前面的结论是正确的。
从以上分析可知,工字型截面梁弯曲正应力强度是否优于矩形截面梁,取决于其宽高比即竖放程度。当工字型截面竖放程度大于或等于矩形截面的竖放程度时,其弯曲正应力强度总是大于矩形截面。当工字型截面竖放程度小于矩形截面的竖放程度时,则对于腹板很矮或很宽的工字型截面,其弯曲正应力强度小于矩形截面;而腹板较高且较窄时,其弯曲正应力强度优于矩形截面。
根据以上分析,现行教材和教学中普遍采用的“工字型截面梁弯曲正应力强度最好,矩形截面次之,圆形截面最差”的表述并不准确。
二、工字型截面梁的最大切应力问题国内现行的材料力学课程教材,在推导平面弯曲梁截面切应力公式后,大都对工字型截面的最大切应力进行分析,并得到该最大切应力等于或约等于截面的剪力除以腹板面积的结论。如刘鸿文[2]教材160页、叶开沅等[3]教材228页、苏翼林[4]教材126页、单辉祖等[5]教材226页、黄小清等[8]教材145页、杨伯源[9]教材146页、赵九江等[10]教材118页、黄世伟[11]教材98页、古滨[12]教材133页、戴宏亮[13]教材107页、王国超[14]教材116页、黄超等[16]教材135页、王吉民[17]教材92页等。还有诸多教材,都有这样的结论,限于篇幅,这里不再一一引述。国外材料力学课程教材也有这样的表述,如铁摩辛柯(Timoshenko,S.P.)等[18]教材165页,铁摩辛柯(Timoshenko,S.)[19]教材128页,E. P.波波夫[20]教材133页等。但此结论忽略了工字型截面尺寸变化对最大切应力的影响,因此仅在一定条件下才成立。此结论对材料力学课程的教与学造成一定困扰,且不利于材料力学的工程应用,下面通过计算对此问题进行分析讨论。
对图 2所示的工字型截面,一般教材都给出了其最大切应力的正确公式,如刘鸿文[2]教材160页中的最大切应力公式,根据该式,有
| $ {\tau _{\max }} = \frac{{{F_s}}}{{8{I_z}{b_1}}}\left[ {{b_1}h_1^2 + b\left( {{h^2} - h_1^2} \right)} \right] $ | (7) |
式中Fs为工字型梁截面上的剪力,Iz为工字型梁截面对截面中性轴的惯性矩,可表示为Iz=[bh3-(b-b1)h13]/12,把Iz代入式(7),通过计算并利用前面引入的工字型截面尺寸参数α和β,式(7)可以改写为
| $ {\tau _{\max }} = \frac{{{F_s}}}{{{b_1}{h_1}}}\frac{{3\alpha \left[ {1 + {\alpha ^2}(\beta - 1)} \right]}}{{2\left[ {1 + {\alpha ^3}(\beta - 1)} \right]}} = \frac{{{F_s}}}{{{A_f}}}p(\alpha , \beta ) $ | (8) |
式中Af=b1h1为工字型截面腹板的面积,Fs/Af为腹板名义平均切应力,也是前述众多教材所认为的工字型截面的最大切应力。p(α, β)为工字型截面最大切应力相对工字型截面腹板名义平均切应力的放大或缩小系数,显然
| $ p(\alpha , \beta ) = \frac{{3\alpha \left[ {1 + {\alpha ^2}(\beta - 1)} \right]}}{{2\left[ {1 + {\alpha ^3}(\beta - 1)} \right]}} $ | (9) |
p(α, β)的等高线如图 5所示。在图 5中,等高值为1的等高线表示工字型截面最大切应力等于腹板名义平均切应力,对于其他截面参数都没有这种关系。
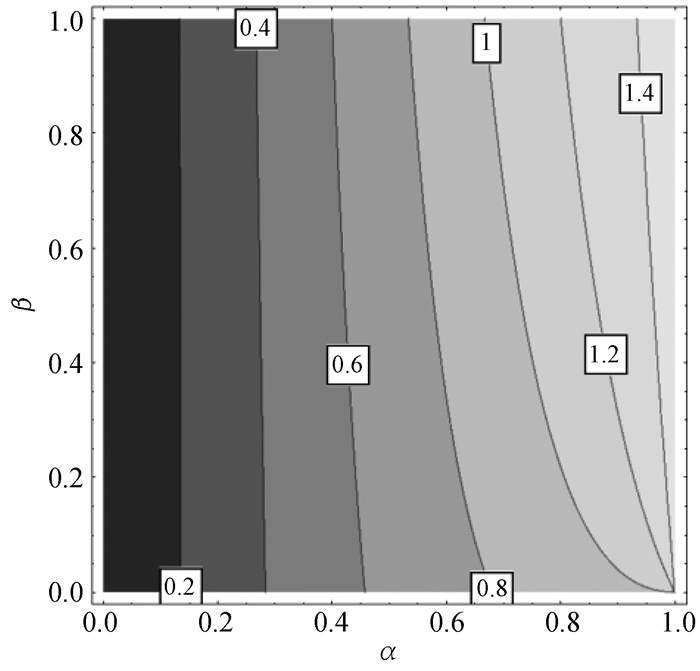
|
图 5 p(α, β)的等高图 |
根据式(9),可知等高值为1所对应的截面尺寸关系为
| $ \beta = \frac{{(2 + \alpha ){{(1 - \alpha )}^2}}}{{{\alpha ^3}}} $ | (10) |
式(10)也可以用图 6表示。
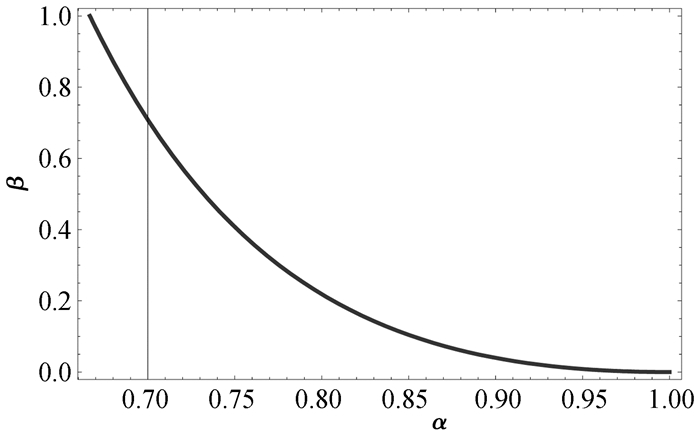
|
图 6 工字型截面τmax=Fs/Af时尺寸参数所需满足的条件 |
由图 5和图 6可知,在图 6曲线右上方的尺寸参数区域,最大切应力大于腹板名义平均切应力,在图 6曲线左下方的尺寸参数区域,最大切应力小于腹板名义平均切应力。可见,现行教材和教学中采用“最大切应力等于腹板名义平均切应力”或“最大切应力近似等于腹板名义平均切应力”的结论只有在式(10)的特定条件下才成立。
算例5.设工字型截面的尺寸分别为b=110 mm, h=220 mm,b1=77.93 mm, h1=154 mm。此时截面的惯性矩为Iz=87.846×106 mm4, 根据式(7),可求得该截面的最大切应力为τmax=83.324 8Fs(N/m2)。而腹板的面积Af= b1×h1=12.00×10-3 m2,所以腹板名义平均应力为Fs/Af=83.324 8Fs(N/m2),可见该截面的最大切应力等于腹板名义平均切应力。又根据该工字钢截面的尺寸,易得α=0.7,β=0.708 455,可见该截面的尺寸系数满足式(10),刚好位于图 6中的曲线上。
算例6.设工字型截面的尺寸分别为b=130 mm, h=320 mm,b1=13.574 2 mm, h1=272 mm。此时截面的惯性矩为Iz=159.744×106 mm4, 根据式(7),可求得该截面的最大切应力为τmax=270.843Fs(N/m2)。而腹板的面积Af= b1×h1=3.69×10-3 m2,所以腹板名义平均应力为Fs/Af=270.843Fs(N/m2),可见该截面的最大切应力也等于腹板名义平均切应力。又根据该工字钢截面的尺寸,易得α=0.85,β=0.104 417,可见该截面的尺寸系数也满足式(10),也刚好位于图 6中的曲线上。
算例7.设工字型截面的尺寸分别为b=120 mm, h=250 mm,b1=90 mm, h1=225 mm。此时截面的惯性矩为Iz=127.773×106 mm4, 根据式(7),可求得该截面的最大切应力为τmax=66.451Fs(N/m2)。而腹板的面积Af= b1×h1=2.03×10-2 m2,所以腹板名义平均应力为Fs/Af=49.383Fs(N/m2),可见该截面的最大切应力大于腹板名义平均切应力,用腹板名义平均切应力代表截面的最大切应力,误差达到31.06%。又根据该工字钢截面的尺寸,易得α=0.9,β=0.75,可见该截面的尺寸系数不满足式(10),而是位于图 6中曲线的右上方区域。
算例8.设工字型截面的尺寸分别为b=120 mm, h=250 mm,b1=36 mm, h1=150 mm。此时截面的惯性矩为Iz=132.625×106 mm4, 根据式(7),可求得该截面的最大切应力为τmax=146.87Fs(N/m2)。而腹板的面积Af= b1×h1=5.40×10-3 m2,所以腹板名义平均应力为Fs/Af=185.185Fs(N/m2),可见该截面的最大切应力小于腹板名义平均切应力,用腹板名义平均切应力代表截面的最大切应力,误差达到26.08%。又根据该工字钢截面的尺寸,易得α=0.6,β=0.3,可见该截面的尺寸系数不满足式(10),而是位于图 6中曲线的左下方区域。
根据算例5、算例6、算例7和算例8可知,本文关于“当工字钢截面参数α,β刚好位于图 6曲线上时,最大切应力等于腹板名义平均切应力;当工字钢截面参数α,β位于图 6中曲线的右上方区域时,最大切应力大于腹板名义平均切应力;当工字钢截面参数α,β位于图 6中曲线的左下方区域时,最大切应力小于腹板名义平均切应力”的结论是正确的。
三、课程教学中提高学生科学素养和培养学生科学研究能力的实践本文关于截面形状对弯曲强度影响的研究过程和方法,以及关于工字型截面弯曲最大切应力与截面腹板名义平均切应力关系的研究过程和方法,为材料力学课程教学中提高学生科学素养和培养学生的科学研究能力,提供了一个良好的案例。一个人的科学素养主要体现在分析问题的能力、解决问题的方法、怀疑一切和证伪一切的精神。
以工字型截面最大切应力为例,当讲解到教材中最大切应力等于腹板名义平均切应力公式时,让学生首先回顾矩形截面最大切应力等于3/2倍截面名义平均切应力、圆形截面最大切应力等于4/3倍截面名义平均切应力的公式,提问学生:这两个公式是否正确?学生会快速回答,因为这两个公式已经证明过,公式是正确的。然后再问:教材中关于工字型截面最大切应力等于腹板名义平均切应力的公式是否也正确呢?学生的反应会相当犹豫,因为教材对此公式没有任何证明,只是通过切应力在截面上主要分布在腹板部分就得到这个公式,所以学生对公式的正确性不敢下结论。怀疑的种子由此萌芽,大脑会快速反应,迫切想知道问题的结论是什么,学生思维活跃起来,接下来有序开展分析。
这时,教师要适时对学生进行引导,让学生对一个任意尺寸的工字型截面的实际最大切应力和腹板名义平均切应力进行课堂练习。如前面的算例7,学生将会很快算出结果,发现在本例中,若用工字型截面腹板名义平均切应力代替工字型截面的实际最大切应力,误差将达到31.06%!学生据此可推出教材中的公式在一些情况下是错误的。教师可适时和学生互动,讨论读书应该秉持的正确态度。通过互动讨论,让学生明白,科学研究的基本素养,就是怀疑一切的精神。有了这种精神,才会努力对所遇到的问题进行分析和研究,才能找出问题背后的规律和真理。
通过上述课堂练习,学生对“工字型截面最大切应力等于腹板名义平均切应力”这个公式已存有疑问,教师可以进一步提问,这个公式是完全错误的吗?学生的思维会进一步被调动起来,这时让学生对满足本文图 6曲线关系的工字型截面的实际最大切应力和腹板名义平均切应力进行课堂练习,如前述算例5。学生也可以很快得到结论,即对于此种尺寸的截面,“工字型截面最大切应力等于腹板名义平均切应力”的结论是成立的。
在一些情况下公式成立,而在另一些情况下公式不成立,那么这个公式与截面尺寸究竟是什么样的一种关系呢?能否找出这种关系?怎么去找出这种关系?由于尺寸参数众多,这样的提问对学生具有很强的挑战性,可以极大地调动学生的兴趣和求知欲。教师可以请学生尝试找出“工字型截面最大切应力与腹板名义平均切应力之间的关系规律”。由于问题的复杂性,学生在课堂上是无法找到这一规律的。但教师可以提示:既然要用工字型截面腹板名义平均切应力表示工字型截面实际最大切应力,那自然应该想到把工字型截面实际最大切应力公式中的尺寸用腹板尺寸表示出来。让学生在这样的提示下进行课后研究,并要求学生在下次课时展示自己的研究结果。
经过课后研究,下次课时,不少学生带来自己的成果。个别学生想到引入尺寸参数,把工字型截面实际最大切应力表示成类似本文式(8)的类型。但由于尺寸参数复杂,学生仍然无法把上述两者关系的规律性讲清楚。这时教师可以把本文工字型截面最大切应力相对工字型截面腹板名义平均切应力的放大或缩小系数,即式(9)的规律性用等高图的方法展示出来。学生通过对等高图的分析,规律性的结论自然显现,学生会有豁然开朗、原来如此的欣喜感和成就感。
通过上述教学实践,引导学生养成要读书但不能迷信书的怀疑精神;通过课堂练习和课后研究,培养学生分析问题和解决问题的能力;通过寻找“用工字型截面腹板名义平均切应力表示工字型截面实际最大切应力”的研究过程,学生初步掌握了运用无量纲方法进行科学研究的方法;体现“工字型截面最大切应力相对于工字型截面腹板名义平均切应力的放大或缩小系数”的等高图分析,展示了寻找自然规律的广阔视野和无限可能。由此,学生的科学素养和科学研究能力都将得到极大的提升。
四、结语关于相同面积条件下各种截面形状对梁弯曲正应力强度的影响,有如下结论:
(1) 当矩形截面横放且宽高比大于1.396 26时,其强度差于圆形截面;当矩形截面横放且宽高比小于1.396 26或矩形截面竖放时,其强度优于圆形截面。
(2) 当工字型截面的竖放程度大于或等于矩形截面的竖放程度时,其强度总是优于矩形截面。
(3) 当工字型截面竖放程度小于矩形截面的竖放程度时,如果工字型截面的腹板很矮或很宽,则工字型截面的弯曲正应力强度差于矩形截面;而当工字型截面的腹板较高且较窄时,则工字型截面的弯曲正应力强度优于矩形截面。
关于工字型截面梁截面上最大切应力问题,有如下结论:
(1) 当工字型截面的尺寸参数α, β满足β=(2+α)(1-α)2/α3时,其截面上最大切应力等于腹板名义平均切应力,即等于该截面的剪力除以腹板面积。
(2) 当工字型截面尺寸参数α, β处于曲线β=(2+α)(1-α)2/α3的右上方区域时,其截面上最大切应力大于腹板名义平均切应力。
(3) 当工字型截面尺寸参数α, β处于曲线β=(2+α)(1-α)2/α3的左下方区域时,其截面上最大切应力小于腹板名义平均切应力。
本文的研究过程和研究方法,为提高学生的科学素养和培养学生的科学研究能力提供了一个良好案例。
| [1] |
孙训方. 材料力学(Ⅰ)[M]. 6版. 北京: 高等教育出版社, 2017.
|
| [2] |
刘鸿文. 简明材料力学[M]. 北京: 高等教育出版社, 1997.
|
| [3] |
叶开沅, 冯燕伟. 材料力学[M]. 北京: 高等教育出版社, 1989.
|
| [4] |
苏翼林, 天津大学材料力学教研室. 材料力学(下册)[M]. 北京: 高等教育出版社, 1988.
|
| [5] |
单辉祖, 谢传锋. 材料力学[M]. 4版. 北京: 高等教育出版社, 2004.
|
| [6] |
范钦珊, 殷雅俊, 虞伟建, 殷雅俊, 范钦珊. 材料力学[M]. 北京: 清华大学出版社, 2008.
|
| [7] |
范钦珊. 材料力学计算机分析[M]. 北京: 高等教育出版社, 1987.
|
| [8] |
黄小清, 陆丽芳, 何庭蕙. 材料力学[M]. 广州: 华南理工大学出版社, 2011.
|
| [9] |
杨伯源. 材料力学[M]. 合肥: 中国科学技术大学出版社, 1998.
|
| [10] |
赵九江, 张少实, 王春香. 材料力学[M]. 哈尔滨: 哈尔滨工业大学出版社, 1995.
|
| [11] |
黄世伟. 材料力学[M]. 武汉: 华中科技大学出版社, 2011.
|
| [12] |
古滨. 材料力学:中学时[M]. 北京: 北京理工大学出版社, 2012.
|
| [13] |
戴宏亮. 材料力学[M]. 长沙: 湖南大学出版社, 2014.
|
| [14] |
王国超. 材料力学[M]. 重庆: 重庆大学出版社, 2014.
|
| [15] |
冯晓九. 材料力学[M]. 北京: 北京理工大学出版社, 2017.
|
| [16] |
黄超, 余茜, 肖明葵. 材料力学[M]. 重庆: 重庆大学出版社, 2016.
|
| [17] |
王吉民. 材料力学[M]. 北京: 中国电力出版社, 2010.
|
| [18] |
铁木辛哥(Timoshenko, S.P.), 盖尔(Gere, J.M.).材料力学[M].陈嘉炜, 等, 译.台湾: 晓园出版社, 1977.
|
| [19] |
铁摩辛柯(Timoshenko, S.).材料力学[M].萧敬勋, 刘文秀, 译.天津: 天津科学技术出版社, 1989.
|
| [20] |
波波夫(E.P.Popov).材料力学[M].马世谋, 译.西安: 陕西科学技术出版社, 1986.
|
 2020, Vol. 29
2020, Vol. 29


