大学生结构设计竞赛是由教育部确定的全国九大学科竞赛资助项目之一，对提高学生的创新思维和实践能力具有重要促进作用^{[1, 2]}。近年来，结构设计竞赛赛题日趋完善，逐渐形成了以竹条、竹皮和502胶水为主要材料的结构模型制作模式^[3]。通过对多年比赛总结发现，以竹皮制作的空心杆逐渐成为结构常用的基本组成杆件^[4]，但不同竹条和竹皮材料组合形式多样^[5]，如何选择合适的截面尺寸，保证结构承受最大荷载的同时，具有质量最轻的空心杆是当前大学生参加结构竞赛时面临的难题。

刘承斌^[6]等对采用白卡纸和蜡线制作构件的抗压和抗拉强度进行了试验，测试结果为结构截面形式的选择奠定了基础；常海林等用竹皮制作了不同尺寸的受拉杆件，测试了其抗拉性能^[7]；贾新聪^[8]开展了若干5 mm×5 mm和7 mm×7 mm方形空心压杆的极限承载力研究，仅给出了竹材受压承载力可取30 MPa，但并未对相应构件的破坏形态进行分类，也未对结构竞赛材料构件选择提出建议；王磊等^[9]测试了边长为5 mm和6 mm三角形和方形空心杆的极限承载力，发现荷质比在120~160 N/g之间，根据荷质比最高原则选择了合适的截面尺寸，但并未对边长更大的构件(边长12 mm)进行测试研究^[10]。

从构件角度优化结构模型，需进行专门的空心受压杆力学性能试验研究，从而为参赛者的截面选择提供依据。本文通过对不同竹皮、竹条类型组合的空心杆截面进行轴压试验和对不同构件破坏形态的分析，测试了构件的质量、极限承载力，并计算其荷质比，得出了不少有益的结论，为学生参与结构设计竞赛时选择构件提供参考，对提高大学生的结构设计竞技水平具有重要意义。

试验采用0.2 mm、0.35 mm、0.5 mm竹皮和2 mm×2 mm、3 mm×3 mm竹条制作了123个边长为5~15 mm的箱型截面受压杆构件。为保证结构为受压破坏，试件长度为100 mm。

主要测试杆件见表 1，表中试件编号分别表示不同试件边长W、空心杆厚度t。D表示单层竹皮，DT表示单层竹皮和竹条组合杆件；S表示双层竹皮，ST表示双层竹皮和竹条组合杆件；2×2 mm和3 mm×3 mm表示采用尺寸为2 mm×2 mm和3 mm×3 mm的竹条做角点。例如，DT353-3509，DT为单层竹皮和竹条，35为竹皮厚度为0.35 mm，3表示竹条边长为3 mm×3 mm，35表示空心杆的厚度为0.35 mm，09表示空心杆的边长为9 mm。

表 1(Table 1)

表 1 试件参数 编号 压杆类型 W/mm t/mm 编号 压杆类型 W/mm t/mm D35-355(5~15) 单0.35 mm+5面 5~15 0.35 S2-4(5~15) 双层0.2 mm 5~15 0.4 D5-505(6~15) 单0.5 mm+5面 6~15 0.50 S35-7(5~15) 双层0.35 mm 5~15 0.7 D5-504(6~15) 单0.5 mm+4面 5~15 0.50 S5-10(5~15) 双层0.5 mm 5~15 1.0 DT352-35(6~15) 单0.35+2 mm×2 mm 6~15 0.35 ST22-4(5~15) 双0.2+2 mm×2 mm 5~15 0.4 DT353-35(7~15) 单0.35+3 mm×3 mm 7~15 0.35 ST23-4(5~15) 双0.2+3 mm×3 mm 7~15 0.4 DT52-50(7~15) 单0.5+2 mm×2 mm 7~15 0.50 DT53-50(7~15) 单0.5+3 mm×3 mm 7~15 0.50

表 1 试件参数

本试验采用的四类杆件类型如下：(1)单层0.35 mm和0.5 mm竹皮制作的空心杆；(2)单层0.35 mm，0.5 mm竹皮，在四个角点放置2 mm×2 mm和3 mm×3 mm竹条制作的空心杆；(3)双层0.2 mm、0.35 mm、0.5 mm竹皮制作的空心杆；(4)双层0.2 mm竹皮，在四个角点放置2 mm×2 mm和3 mm×3 mm竹条后制作的空心杆。

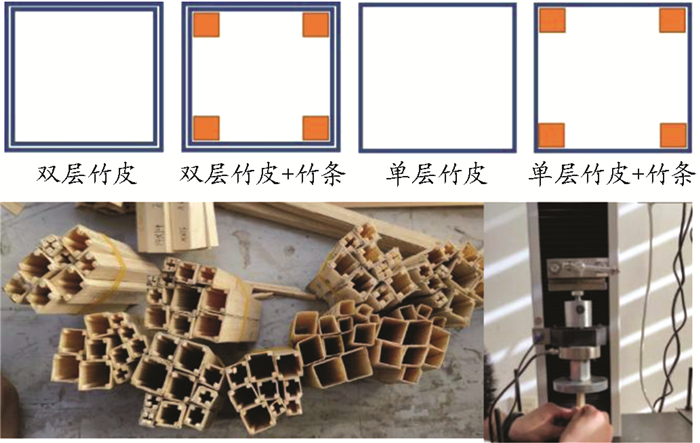
试验采用的竹皮和竹条均购于同一材料厂商，试件制作过程中尽量选用材质均匀、竹节少的材料。箱型空心杆的制作采用先在竹片顺纹方向上用刀背刻痕，然后再沿刻痕方向折叠成空心杆件，在竹皮折叠处滴胶，拟补折叠划痕和材料原有的缺陷^{[3, 10]}。如图 1给出了制作的空心杆。

图 1(Figure 1)

图 1 试件构件及加载过程示意图

试验装置采用济南川佰试验仪器有限公司生产制作的电子拉、压试验机，试验最小分辨率为1 N，试验受压行程为80 cm，试验以每分钟10 mm的速度加载，试验机自行采集荷载峰值和位移值，并绘制荷载—位移曲线。当出现试件破坏或断裂时，加载过程自动终止并回弹。图 1给出了加载过程示意图。

对大量试验结果分析发现，构件主要发生三种破坏：(1)端部侧面竹皮局部屈曲导致的杆端局部破坏；(2)某中间截面折断引起的失稳屈曲破坏；(3)竹皮或棱角开裂导致的侧棱黏结处开裂破坏。由表 2不同类型构件的破坏类型统计结果可知，单层竹皮构件以棱角处折痕破裂为主，约占总破坏的80%，原因为竹皮在棱角处刻痕对折后，连接作用明显减弱，在外荷载作用下，容易发生开裂；双层竹皮制作的空心杆，以屈曲破坏为主，占总破坏的67%，除手工制作原因外，一般不会出现棱角开裂情况，主要原因为双层竹皮增加了构件侧面连接性，但由于杆件中间部位竹皮存在缺陷或达到屈曲而出现该种破坏。

表 2(Table 2)

表 2 不同破坏形态杆件数统计分析 试件类型 杆端局部破坏 失稳屈曲 侧棱黏结处开裂 单层0.35+5面 2 4 5 单层0.5+4面 1 1 8 单层0.5+5面 5 1 4 双层0.2 mm 2 9 0 双层0.35 mm 0 9 2 双层0.5 mm 6 4 1 单层0.35 mm+2 mm×2 mm 7 2 1 单层0.5 mm+2 mm×2 mm 6 1 2 单层0.35 mm+3 mm×3 mm 5 3 2 单层0.5 mm+3 mm×3 mm 4 3 2 双层0.2 mm+2 mm×2 mm 5 5 1 双层0.2 mm+3 mm×3 mm 10 0 0 合计 53 42 28

表 2 不同破坏形态杆件数统计分析

单层竹皮棱角设置4根2 mm×2 mm竹条后，端部破坏占总破坏的58%。双层竹皮加3 mm×3 mm竹条的组合构件，端部断裂占整体破坏形式的比例进一步增大，达到71%。证明通过刚度较大的竹条可增大棱角处竹皮的连接性和整个截面刚度，从而提高了结构极限承载力。

1.端部断裂

该破坏形式是由于局部受压端竹皮的刚度较压力机受压钢板刚度小，杆件端部竹皮的局部屈曲破坏引起的，如图 2所示。实际模型除了安装支座处外，一般不会发生此破坏类型。

图 2(Figure 2)

图 2 端部破坏形态

2.中间截面断裂

一般在1/2和1/3截面之间最容易发生局部受弯屈曲破坏，如图 3所示。理想构件处于受压状态，实际在外力作用下，可能会受到弯矩和轴压共同作用。若构件中间某个截面的竹皮存在局部缺陷，则会导致构件产生局部屈曲破坏，从而整体出现受弯破坏。在手工制作过程中，可仔细查找竹皮的节点等容易破坏的位置，将其贴成双层竹皮，以减小由于局部缺陷引起该种破坏形态的发生。

图 3(Figure 3)

图 3 跨中破坏形态

3.竹皮或棱角开裂破坏

应该避免受压空心杆的竹皮或棱角开裂破坏，如图 4所示。多数破坏出现在中间竹皮，主要原因为竹皮存在顺纹裂纹，构件选材时可选择缺陷少的构件，从而避免此类破坏的出现。但棱角处破坏在单层竹皮结构中出现的几率较大，可通过在棱角处粘贴0.2 mm竹皮的方式提高其承载力。

图 4(Figure 4)

图 4 棱角开裂破坏形态

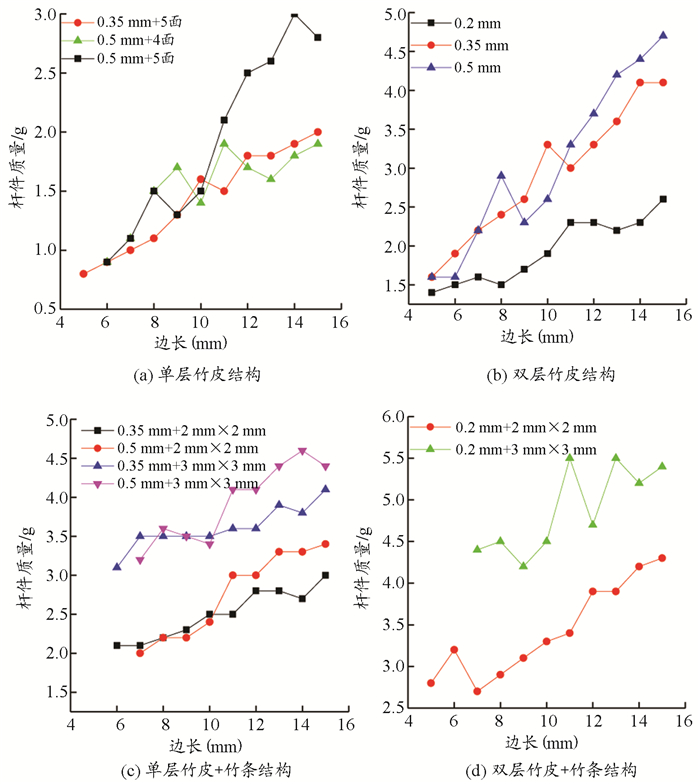
由图 5给出了四类不同杆件的质量随空心杆边长的变化曲线可知，0.35 mm制作5个面的质量与0.5 mm制作4个面的相差不大。当采用双层竹皮后，质量迅速增加，且0.2 mm厚竹皮的质量较0.35 mm和0.5 mm竹皮的质量明显小。单层竹皮在角点放置2 mm×2 mm和3 mm×3 mm的竹条后，质量提升较大。

图 5(Figure 5)

图 5 构件质量随边长变化关系

1.极限承载力与试件宽度的关系

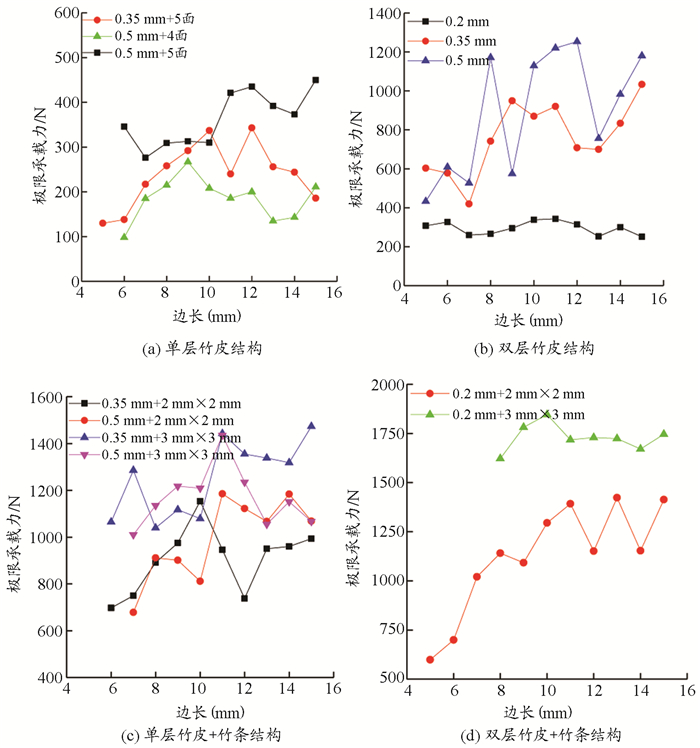
由图 6给出了四类不同杆件极限承载力随边长增加曲线可知，各类空心杆的极限承载力随边长的增加呈现出先增加后降低的趋势(或趋于稳定)。

图 6(Figure 6)

图 6 构件承载力随边长变化关系

单层竹皮制作空心杆的承载力在100 N~350 N之间，仅0.5 mm竹皮+5个面构件的承载力超过400 N。单层竹皮构件边长在8 mm~12 mm之间时，承载力最高，原因是边长增大后，单边容易发生屈曲，导致构件承载力降低，这也是目前国内比赛一般不采用边长大于10 mm空心杆的主要原因。对单层竹皮制作的空心杆，以0.35 mm或0.5 mm竹皮，边长为10 mm为最优选择，极限承载力能达到300 N。

将竹材变为双层后，随边长增加，极限承载力呈现出先增加后减小趋势，且边长在10 mm时承载力较高。竹皮由单层变为双层后，构件的极限承载力明显提升，0.35 mm竹皮承载力由300 N升为1000 N，0.5 mm竹皮承载力由280 N升为1200 N，主要原因为双层竹皮增加了侧边局部稳定性。而0.2 mm竹皮制作的空心杆承载力随边长增加几乎不变，承载力仅有230 N左右。所以，0.2 mm双层竹皮适合制作受力较小的次要杆件，且边长适合采用5 mm。

在0.35 mm和0.5 mm单层竹皮制作的空心杆四角设置竹条后，极限承载力进一步提高，以0.35 mm竹皮+3×3竹条制作的空心杆承载力最高，承载力可达2000 N，但质量增加2.5倍，对受力特别复杂的构件，可考虑该种结构。另外，0.35 mm竹皮+3 mm×3 mm竹条的杆件极限承载力较0.5 mm竹皮+3 mm×3 mm竹条杆件的极限承载力大，但前者质量明显小于后者，证明前者在提高构件承载力方面具有更大的优势。0.35 mm竹皮+2 mm×2 mm竹条杆件极限承载力较0.5 mm竹皮+2 mm×2 mm竹条杆件的极限承载力小，但其承载力较0.35 mm单层竹皮提高约4倍。

双层竹皮+2 mm×2 mm或3 mm×3 mm竹条制作的构件极限承载力会进一步提高，对目前结构设计竞赛的模型而言，仅适合受力特别复杂位置采用。

2.极限承载力与竹皮厚度的关系

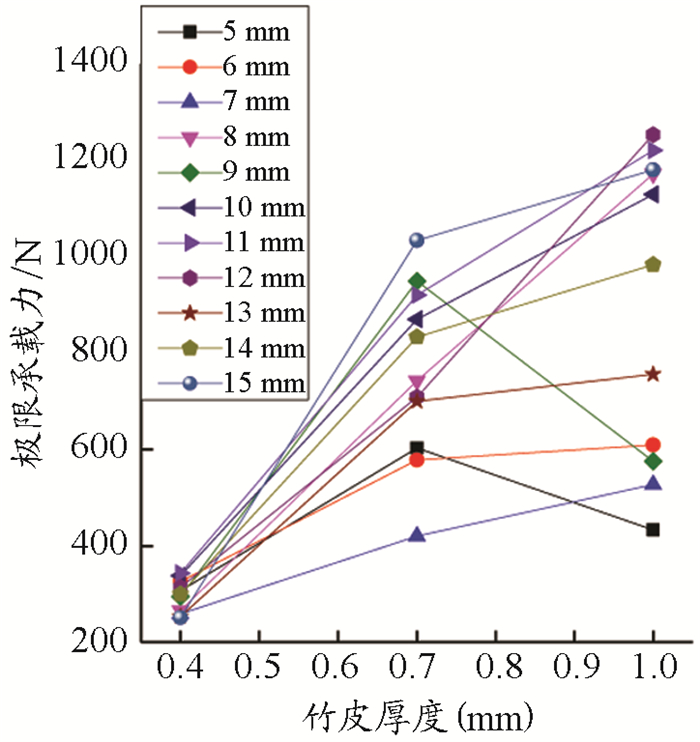
由图 7给出了极限承载力随着竹皮厚度变化的情况可知，对双层竹皮而言，随竹皮厚度增加，承载力逐渐提高，即采用0.5 mm竹皮制作的双层空心杆具有较高承载力。边长为10 mm和11mm的空心杆，在利用各种厚度竹皮时，均有较高承载力。

图 7(Figure 7)

图 7 构件极限承载力与竹皮厚度的关系

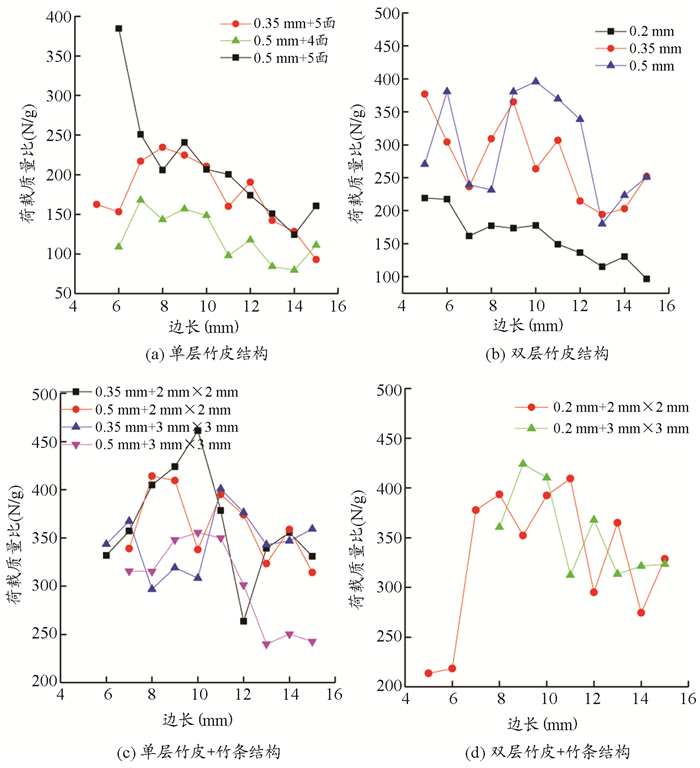
由图 8给出了各类构件的极限荷载与质量之比(荷质比)随杆边长变化曲线可知，双层竹皮构件的荷质比随着边长增加而降低，证明尺寸越小，构件基本不会发生局部屈曲破坏。对于截面边长较大的构件，可增加横隔板的方式提高局部稳定性。

图 8(Figure 8)

图 8 构件荷质比随边长变化关系

单层竹皮制作空心杆的荷质比随边长的增加逐渐降低，且0.35 mm+5面的构件荷质比(100~200 N/g)大于0.5 mm构件+4面(50~150 N/g)。0.35 mm+5面的构件荷质比与0.5 mm+5面的构件荷质比相差不大，说明虽然0.5 mm竹皮具有较高承载力，但并不能有效提高荷质比，0.35 mm和0.5 mm竹皮空心杆需根据结构受力情况选取。本文测试的荷质比较文献^[9]的试验结果低。

在双层竹皮构件中，0.5 mm竹皮构件的荷质比最大，可达400 N/g，0.35 mm竹皮构件荷质比居中，在200 ~350 N/g之间；0.2 mm构件荷质比最小，在100~200 N/g之间。证明对双层竹皮构件，以0.5 mm竹皮为主，且构件边长以小于10 mm较为合理。

单层竹皮四角加竹条后，荷质比明显提高，均大于250 N/g，且随着边长增大而减小。0.35 mm+2 mm×2 mm竹条在边长为10 mm时，荷质比可达460 N/g，且将2 mm×2 mm竹条换成3 mm×3 mm竹条后，荷质比提高不明显。证明0.35 mm+2 mm×2 mm竹条在边长为10 mm时，承载力能达到理想效果，是单层竹皮加肋构件的最佳选择。0.5 mm+2 mm×2 mm竹条制作构件的荷质比大于0.5 mm+3 mm×3 mm竹条构件。

双层竹皮加竹条后，荷质比较双层竹皮构件有一定提高，但与单层竹皮四角加竹条的相差不大，证明双层竹皮加四角加肋构件对提高构件的整体承载力有限，并非最佳选择。其荷质比也随着边长增加而降低，最大为边长为8~10 mm。

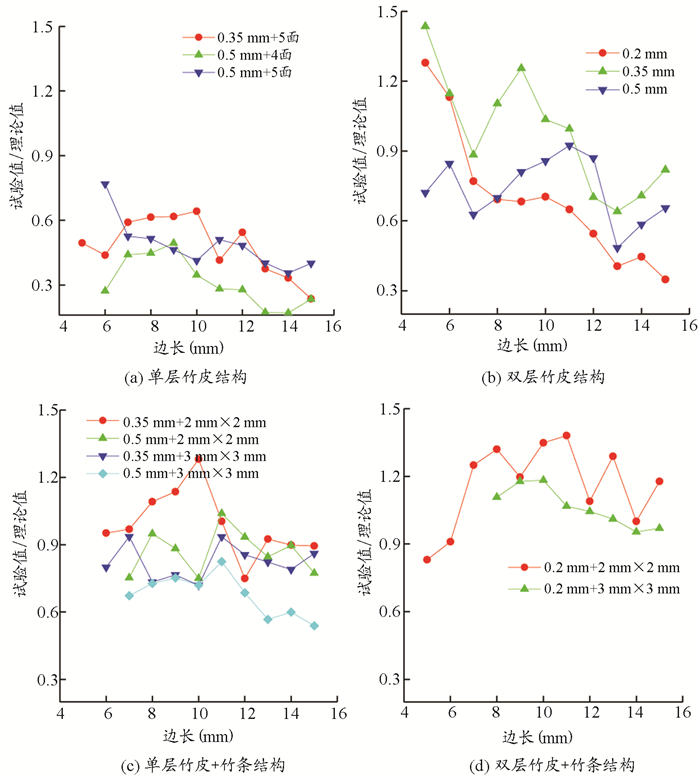
由于本次制作构件均为轴心受压短柱，理论计算时不考虑轴心受压屈曲破坏，理论极限承载力为截面面积与抗压强度乘积，其中竹材强度取结构设计大赛赛题中给出的理论抗压强度30 MPa^[7]。为探讨手工制作质量对空心杆极限承载力的降低作用，图 9给出了实测极限承载力与理论计算值随受压空心杆边长的对比情况。

图 9(Figure 9)

图 9 试验值与理论计算值对比

由图 9可知，单层竹皮轴压杆的试验值与理论值之比小于0.6，除双层竹皮构件在边长大于10 mm时比值小于0.6外，其余空心杆的比值均大于0.6，有的甚至超过1.0，说明单层竹皮空心杆的手工制作质量较差，空心杆四角较容易出现局部屈曲问题，若想按照理论设计值进行模型设计，需考虑手工制作引起的极限承载力降低作用。另外，图 9(a)显示，单层竹皮构件的试验与理论比值随边长增大而减小，0.35 mm+5面的单层空心杆在边长低于10 mm时，比值大于0.6，是单层竹皮构件的最佳尺寸选择。

由图 9(b)可知，双层竹皮空心杆的试验值与理论值之比也随边长增加逐渐降低，且0.35 mm双层空心杆因手工制作导致的承载力降低较小，比值基本能达到0.9以上；0.2 mm双层空心杆在边长大于7mm后，质量不宜保证，不适合制作边长大于7 mm的受压构件。

与纯单层和双层竹皮构件相比，在四角加上竹条，将空心杆最容易出现问题的角点这个薄弱环节予以补强，从而导致因手工制作水平差异导致的承载力降低减小，且试验与理论比值不随边长的增大而降低，单层竹皮+2 mm×2 mm竹条结构的手工制作降低作用大于单层竹皮+3 mm×3 mm竹条构件，且承载力较高；双层竹皮+竹条结构的试验值与理论值之比大于0.9，基本不会因手工制作降低承载力；虽然单层和双层竹皮加竹条结构的荷质比提高有限，但单层竹皮+2 mm×2 mm竹条和双层竹皮构件的手工制作水平较容易保证，较适合设计模型中受力较大的构件。

本文开展了不同类型空心杆的受压承载力试验研究，分析了不同构件的破坏形式、质量、极限承载力和荷质比。主要得出以下结论：

(1) 受压空心杆的破坏形式主要有：端部局部破坏、中部失稳屈曲破坏和侧棱开裂破坏。单层竹皮构件以棱角开裂为主，双层竹皮构件以受弯破坏为主；在手工制作中，可控制截面边长在10 mm内，防止中部失稳屈曲破坏；在角点设置包角，防止棱角开裂破坏；

(2) 空心杆极限承载力随边长的增加呈先增加后降低的趋势，最佳边长为8~12 mm。单层竹皮构件的极限承载力在200~300 N，双层竹皮构件可达1000 N，竹皮加竹条组合构件承载力可超过1200 N；

(3) 单层竹皮构件的荷质比较小，且0.35 mm+5面构件的荷质与0.5 mm+5面构件相差不大；双层竹皮构件以0.5 mm竹皮空心杆具有最优荷质比(达到400 N/g)，适合承载力较大的构件制作；双层竹皮或单层竹皮+竹条结构的荷质比较双层竹皮结构提高有限，且随着边长增大而减小，仅适合于受力特别复杂的构件。

(4) 单层和双层竹皮构件的试验值与理论值之比随边长的增加而降低，说明边长越大，因手工制作对构件极限承载力的降低作用越明显；0.35 mm+5面的单层空心杆在边长小于10 mm时，手工制作质量会导致理论承载力降低40%；竹皮+竹条结构的试验值与理论值之比随边长的增加变化不明显，手工制作引起的承载力降低小于10%。