2. 清华大学 水利系, 北京 100084
2. Department of Hydraulic Engineering, Tsinghua University, Beijing 100084, P. R. China
改革开放以来,国民经济迅速发展,无形中也促进了岩土工程技术的进步,特别是岩土工程施工工艺技术方面成绩斐然。然而由于历史原因,我国大陆的岩土工程相关规范受苏联的影响很大,导致这些规范在设计计算方法上,与其他欧、美、日等发达国家和地区的差异很大,使得我国国标等规范难以应用于境外的工程项目,再加上境外地区的岩土工程项目,其咨询、设计与监理多整合为一体,以致我国岩土工程从业企业只能参与勘察或施工项目的工作,难以开展咨询、设计与监理的竞标。这一实际现状,不仅导致企业难以获得理想的利润,也制约着我国岩土工程的发展。
此外,随着我国国际影响力的增加,岩土工程的咨询、勘察、设计、监理与施工等技术的控制与管理工作,如何与国际接轨的问题也日趋突出[1]。要解决这一关键问题,除了要开展相关标准与系统的整合研究外,关键仍在做好新时期岩土工程专业人才的培养工作。有鉴于此,本文从岩土工程设计理念着手,从土力学的教学视角讨论安全系数的取值问题,并以基础的地基承载力与边坡稳定分析的计算原理为例,探讨我国现行规范与欧、美、日等国家和地区常用设计计算公式的差异,分析我国标准的不足之处,以期为我国岩土工程人才的培养提供新的借鉴与思考。
一、岩土工程的设计方法 (一) 容许应力设计法早在19世纪初,随着工业革命的发展,许多强度高的新材料(如铁、钢等)可以被大量生产制造,这使得传统经验或试误的设计方法无法满足建设发展的需要,也因此萌生了基于古典力学理论的容许应力设计法(allowable stress design)[2],并应用于结构工程、岩土工程与水利工程等土木工程的建设中,人们可以开始安全、经济且高效地构筑所需的建筑物,极大地促进了近现代土木工程的发展。
容许应力设计法也被称为工作应力设计法(working stress design),其设计概念是通过结构构件的极限应力与适合的安全系数,得出可供设计用的容许应力,其代表着结构构件所能承受的工作应力。也就是说,结构构件所处的应力若小于其容许应力,则该构件在设计意义上不会被破坏。以浅基础的地基承载力为例[3],其数学表达式可写为:
| $ \frac{{F + G}}{A} \le {q_{{\rm{all}}}} = \frac{{{q_u}}}{{FS}} $ | (1) |
式中,F为上部结构传递至基础顶面的荷载(kN); G为基础和基础以上土的自重(kN);A为基础底面积(m2);qall为容许承载力(kPa);qu:极限承载力(kPa);FS为安全系数。
工程实践中也可根据工程师的设计习惯,采用净容许承载力qall(net)的概念设计,即
| $ \frac{F}{A} \le {q_{{\rm{all(net)}}}} = \frac{{{q_u} - q}}{{FS}} $ | (2) |
式中,q为基础底面以上土的有效自重应力(kPa)。
从式(1)与式(2)不难看出,容许应力设计法的关键核心在于极限承载力与安全系数的决定。但在实践过程中发现,安全系数的决定有时非常困难,过大的安全系数导致工程设计过于保守,造成工程投资的浪费,而过小的安全系数则会导致额外的风险[2]。此外,局部构件达到强度并不意味着整体结构的破坏,而结构可接受的损坏程度也随着构件的重要性以及荷载条件的不确定性而变化[4]。这些因素都使得容许应力设计法已不能满足在保证安全的前提下,最经济的设计需求。
举例来说,在基础设计中,地基的稳定性与基础允许变形的要求明显不同,若只考虑相同的安全系数,往往不能充分发挥地基的承载能力,亦即不能更经济且有效地设计[5]。因此,为了更合理地考虑结构的环境条件与新材料的有效应用,便发展出基于可靠度理论的极限状态设计法(limit states design)。
(二)分项系数法实践中发现,采用可靠度设计法对结构物所涉及的荷载和抗力均进行概率分析是不现实的,因此一种简化的可靠度法——因数设计法(factor design)被提出,这一方法的典型代表如我国的分项系数法[5]与美国的荷载与抗力因数设计法(load and resistance factor design, LRFD)[6]。简单来说,其是利用可靠度理论将荷载与抗力分别考虑不同的系数,来表示结构物在使用阶段中可能承受的荷载以及材料所能提供的抗力(分别考虑荷载与抗力的可靠度),并以此来进行结构设计,其数学表达式可写为
| $ {\gamma _R}{R_k} \ge \sum {\gamma _i}{Q_i} $ | (3) |
式中,γR为抗力的分项系数;Rk为抗力的标准值;γi为第i个荷载效应的分项系数;Qi为第i个荷载的标准值。
式(3)可看出,分项系数法与容许应力法相比,其安全系数不再唯一。时至今日,对于结构工程来说,除了少部分特殊情况外,如钢结构的疲劳计算,其余基本采用分项系数法设计[7]。而对于岩土工程来说,仍需开展更多且更系统的整合研究,才能以分项系数法设计。
(三)岩土工程的设计考量目前岩土工程的设计理念多采用基于容许应力概念的极限状态设计法,即同步考虑承载能力的极限状态与正常使用的极限状态。以基础设计来说,需同时满足基底压力要小于容许地基承载力,以及地基的变形要小于设计的容许值。
尽管我国大陆在岩土工程设计理念的关键核心与其他国家和地区差异不大,但在建议的计算方法上差异则非常明显,特别是在承载能力极限状态的验算上,部分规范仍停留在经验容许值。如:公路桥涵地基与基础设计规范(JTG 3363-2019)利用岩土类别、状态及其物理力学特性指标与工程经验,查表得出地基承载力的基本容许值[8]。由于基础的地基承载力,不仅与土的抗剪强度指标(c', ϕ')密切相关,也与基础型式(形状、宽度B与埋深Df)有关,仅依据土的孔隙比、含水量与液性指数等物理性质来决定容许承载力,显然会有较大的误差,且其潜在风险也不易被评估。从古典力学的发展历史来看,这种方法已不适合简单归纳到前述的容许应力设计法里。
如前所述,容许应力设计法的核心在通过力学手段求得极限承载力,再考虑合适的安全系数进行工程设计,因此这一方法的关键在于安全系数的取值,亦即可通过安全系数取值的分析,了解我国大陆规范的设计方法与其他国家和地区的差异,而这也有助于消除土力学或基础工程教学过程中学生常见的思维误区,以完善相关的知识体系,提高国际竞争力。此外,这一讨论也可为我国规范的修订、推广和应用,提出新的思路与借鉴。
二、安全系数取值的思考与讨论 (一) 浅基础地基承载力的计算由于地基极限承载力的决定是应用容许应力设计法的重要基础,因此早在20世纪20年代开始,有非常多的学者(如:Prandtl, Reissner, Terzaghi, Meyerhof, De Beer, Hansen, Vesic等)针对浅基础的地基极限承载力问题,开展了大量的研究工作[3, 9],最终总结出地基的极限承载力公式;且为了便于工程实践,对基础形状、埋深与荷载倾斜对极限承载力的影响加以修正,提出了更具一般性的广义极限承载力公式。这一公式也成为欧、美、日等发达国家和地区估算浅基础地基极限承载力的基本方法,而不同国家和地区,依据其土性特点与工程经验,选择不同的承载力系数Nc、Nq与Nγ的数值,以及形状、埋深和荷载倾斜的修正系数公式。
我国大陆受苏联的影响,相关学者依据多数基础事故是由变形主控的这一实际现象,且变形是基于线弹性原理计算而得,因此利用弹性附加应力计算公式结合Mohr-Coulomb强度准则,来验算地基在荷载作用下是否处于弹性变形状态,并以此得出设计所需的地基承载力特征值[5, 10],其代表规范为建筑地基基础设计规范(GB 50007)。
显然,由于设计理念的不同,这两者在浅基础地基承载力计算结果上的差异也非常明显;且由于历史原因,世界上多数国家和地区均采用基于Terzaghi等人的研究成果进行设计工作,这使得我国规范的推广遇到一定的困难,且无形中制约了我国企业开展国际岩土工程项目的设计业务。为了了解这两者设计理念的差异,以下通过简介、举例与讨论进行阐述。
1. 广义极限承载力公式广义极限承载力公式的数学表达式可写为[3]
| $ {q_{\rm{u}}} = c'\cdot{N_c}{F_{cs}}{F_{cd}}{F_{ci}} + q\cdot{N_q}{F_{qs}}{F_{qd}}{F_{qi}} + \frac{1}{2}\gamma B\cdot{N_\gamma }{F_{\gamma s}}{F_{\gamma d}}{F_{\gamma i}} $ | (4) |
式(4)中,Fcs、Fqs、Fγs为形状修正系数;Fcd、Fqd、Fγd为埋深修正系数;Fci、Fqi、Fγi:荷载倾斜修正系数。常用的修正系数的计算公式见表 1。
| 表 1 形状、埋深与荷载倾斜的修正系数公式 |
尽管我国建筑地基基础设计规范并没有采用式(4)计算极限承载力,但这一概念在一些土力学教材里也有介绍,并将其称为Hansen极限承载力公式[9]。
对于偏心荷载基础,则采用Meyerhof建议的有效面积的概念来估算基础所能承受的荷载[14],此时基础按偏心后的有效尺寸计算地基的极限承载力,而有效面积随偏心距增大而减少,使得基础所能承受的荷载也相应减少。
得出极限承载力后,即可考虑合理的安全系数以求得容许承载力。一般情况下,安全系数不小于3;而对于短期荷载,如地震、风和雪荷载,安全系数可适当取小,但仍需在2以上。
2. 地基基础设计规范(GB 50007)——浅基础的地基承载力公式地基基础设计规范建议的浅基础地基承载力特征值fa(kPa)可以表示为
| $ {f_a} = {M_b}\gamma b + {M_d} \cdot q + {M_c}{c_k} $ | (5) |
式(5)中,Mb、Md、Mc为与ϕk有关的承载力系数;b为基础宽度(m),大于6 m按6 m取值,对于砂土小于3 m按3 m取值;γ为基础底面以下的土的有效容重(kN/m3);ck、ϕk分别为基底下一倍短边宽深度内的有效黏聚力(kPa)和有效内摩擦角(°)的标准值。
式(5)基本上是采用塑性区发展深度为基础宽度的1/4所对应的临界荷载p1/4作为地基承载力特征值,并根据实践经验对ϕ>20°的情况适当提高基础宽度承载力系数Mb值,且适用于基本没偏心(偏心距e≤b/30)的条件。
然而,工程实践中有时所面临的基础荷载为小偏心荷载(e≤b /6),按规范建议则不能使用规范公式计算。由于初步设计时,往往还未开展平板载荷试验或运用其他原位测试手段,这使得许多工程师还是利用规范公式或是更为粗糙的经验查表法设计,这无形中弱化了设计理念的严谨性,不利于我国规范的推广。
此外,我国规范建议公式的设计理念在校核地基在荷载作用下是否处于弹性状态,其本质上仍属于容许应力设计法的思路。此时,FS=qu/fa,且由于fa的推导过程与假设FS不再唯一,这使得工程师在设计时,将不易评估相应的风险。
对于偏心荷载问题,规范规定
| $ {p_{k{\rm{max}}}} \le 1.2{f_a} $ | (6) |
式(6)中,pkmax为基础底面的最大压力值(标准组合,kPa)。
从式(6)可看出,其允许基底最大压力超过基础承载力特征值。然而,偏心荷载是长期存在的,却可提高其能承受的承载力,这也有违常规的设计逻辑。当然,这也说明了采用弹性状态校核而得出的承载力特征值,其设计理念与承载能力极限状态的校核仍有一定的区别。此外,承载力特征值的概念也涉及“临界”荷载的概念,而这一“临界”概念,与一般中文字义的理解不同,容易使学生产生混淆,不利于学生理解,因此在土力学教学过程中需重点关注和强化这一问题,以利于学生工程设计逻辑思维的培养。
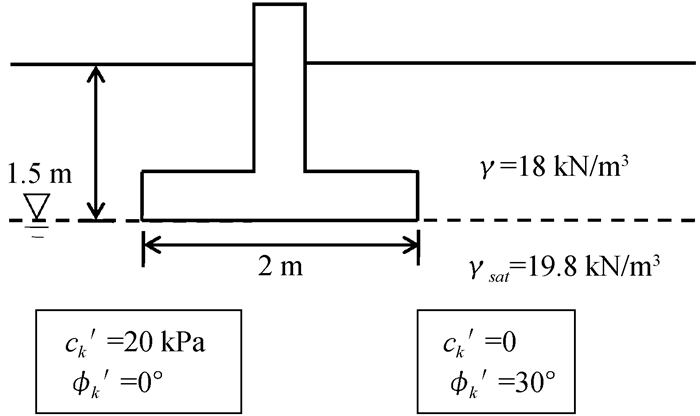
3. 算例分析与讨论本文利用方形与条形基础地基承载力的算例以直观地了解上述这两种方法在设计上的差异,基础下方饱和粘土层的总应力(ϕ=0设计)与有效应力(c=0设计)强度指标的标准值如图 1所示。且为了计算方便,将地下水位设于基础底面,即不考虑地下水位对滑动土体自重的修正问题,并假设地基土若发生局部剪坏模式,则依据Terzaghi的建议进行ϕ的折减,修正承载力系数值,且承载力系数采用Vesic提出的建议值[15],如此即可利用式(4)与表 1计算广义极限承载力,其结果如表 2所示。
|
图 1 坐落于饱和粘土层的浅基础 |
| 表 2 地基极限承载力与承载力特征值的比较 |
计算结果可看出
(1) 对于ϕ=0设计,qu/fa基本小于2。这说明对于饱和软土的不排水条件设计,采用规范建议公式计算,所得的结果偏危险。
(2) 对于c=0设计,若地基破坏模式为整体剪坏,则qu/fa均大于4。即对于排水条件设计,采用规范建议公式计算,所得的承载力特征值较保守,而这一结果同样也适用于粗粒土地基。
(3) 尽管规范建议公式仅适用于荷载没偏心的条件,但对于方形和矩形基础的c=0设计或粗粒土地基,若地基破坏模式为整体剪坏,则利用规范公式计算小偏心荷载的基础,仍有一定的安全储备;但对于承受大偏心荷载的条形基础,采用规范公式计算,仍需注意其潜在风险。
(4) 倘若地基出现局部或冲剪破坏模式,如依据Terzaghi的建议进行ϕ的折减,则因承载力系数的降低,将导致qu大幅减少,此时规范建议公式对c=0设计或粗粒土地基,并没有提供较为保守的地基承载力设计值。这一结果也说明,采用极限承载力设计,地基剪坏模式的判断及其合理修正的问题非常重要。
简言之,在软土的不排水设计、地基发生局部或冲剪破坏模式,采用建筑地基基础设计规范的计算方法有可能导致较大的设计风险。
此外,这一算例也说明,在土力学教学过程中,不宜仅介绍我国规范的建议公式及其计算方法,而需强化学生对土力学基本理论的理解,并适当剖析我国现行规范的设计思路与古典力学的内在联系,以利于评估相应的设计风险,提高学生优化设计的水平与能力。而此举也有助于在参与境外岩土工程项目时,可较快地掌握相关的设计规范与标准。
(二)桩基础的地基承载力计算与浅基础一样,我国大陆对桩基础承载力的设计理念也与其他国家和地区差异不大,以竖向单桩承载力为例,其基础型式均可表示为
| $ {Q_u} = {Q_p} + {Q_s} = {q_p}{A_p} + u\sum {q_{si}}{l_i} $ | (7) |
式(7)中,Qu为单桩竖向极限承载力(kN);Qp为单桩总极限端阻力(kN);Qs为单桩总极限侧阻力(kN);qp为极限端阻力(kPa);qsi为桩侧第i层土的极限侧阻力(kPa);Ap为桩端底面积(m2);u为桩身周长(m);li为桩侧第i层土的厚度(m)。
在具体的计算方法中,我国桩基规范(JGJ 94- 2008)仍给出经验参数法的建议,即利用土的状态与桩型依据经验查表取值[16],而多数国家和地区则利用古典力学方法结合工程经验计算得出[17](对于粗粒土地基,也考虑了端阻力与侧阻力的临界深度问题)。同样,这一简化做法也不利于我国规范的推广。
即使避开这一问题不谈,采用经验查表法所得的单桩竖向极限承载力标准值与其他方法(如:单桩竖向静载荷试验)相同,都只考虑“2”的安全系数,即可得出单桩竖向承载力特征值,而这导致许多学生不能理解安全系数取值的标准,也不利于培养学生工程设计的逻辑思维。因此在土力学教学过程中同样也需强化学生对容许应力设计法的理解,并适当指出现行规范的不足之处,以利于我国规范的完善与发展。
(三)边坡稳定分析的基本概念容许应力设计法的概念同样也可应用于边坡稳定分析,此时与一般工程设计不同,FS变为待求的未知数,并可令其为潜在滑动面上土的平均抗剪强度τf与其作用的下滑剪应力τd的比值,若假设τf与τd可表示为Mohr-Coulomb准则的型式,则
| $ FS = \frac{{{\tau _f}}}{{{\tau _d}}} = \frac{{c' + \sigma '{\rm{tan}}\phi '}}{{c{'_d} + \sigma '{\rm{tan}}\phi {'_d}}} $ | (8) |
式(8)中,σ′为潜在滑动面上的正应力(kPa);c'd为下滑剪应力的有效黏聚力分量(kPa);ϕ'd为下滑剪应力的有效内摩擦角分量(°)。
从式(8)可看出,对于ϕ=0设计;FS=c'/c'd=黏聚力分量的安全系数Fc;对于c=0设计;FS=(tanϕ')/(tanϕ'd)=内摩擦角分量的安全系数Fϕ。此时,一些学生认为可对黏聚力与内摩擦角分别考虑不同的安全系数来评价边坡的稳定性。从单纯的数学计算来看,这一做法似乎没有问题,但由于边坡稳定分析安全系数的概念是基于容许应力设计法,倘若Fc≠Fϕ就不能将潜在滑动面上土所提供的抗剪强度与所作用的应力联系起来,进而违背基本的理论架构,因此在应用这一概念分析边坡稳定性时,FS=Fc=Fϕ。从这一例子来看,土力学的问题不能简单视为数学游戏,其背后隐含着工程设计的基本原理与内涵,因此在土力学教学过程中也需对此加以关注,才能较好地培养学生工程设计的逻辑思维。
三、结语通过上述分析与讨论,可看出尽管我国现行规范的设计基本理念与其他国家和地区差异不大,但由于受苏联的影响,在计算方法上的差异则非常明显,甚至部分规范还保留经验查表法。这一做法无形中弱化了我国规范的影响力,且不利于将其推广和应用至世界其他国家和地区。
此外,随着我国国民经济的迅猛发展,岩土工程积累了大量的实践经验。这些经验是优化设计方法的重要基石,倘若能系统地收集与整理室内与现场试验的结果,并设置于岩土工程信息平台里,再结合相应的科学研究,将有助于构建新的设计方法与标准。如此不仅可大幅提高我国岩土工程的设计水平,也有利于我国设计标准的推广与应用。
在学生工程设计逻辑思维的训练上,建议强化土力学基本理论知识的理解,在教学中尽可能地剖析我国规范的设计原理及考量因素的内在联系,并辅以基于古典力学的计算方法的介绍,最后再结合计算能力的强化训练,这样有利于学生日后参与境外岩土工程项目时,能够较快地掌握相关设计规范与标准。而对岩土工程专业人才的这一训练与培养,可为我国岩土工程相关企业奠定坚实的人才储备基础。
| [1] |
顾宝和. 浅谈岩土工程的专业特点[J]. 岩土工程界, 2007(1): 19-23. DOI:10.3969/j.issn.1674-7801.2007.01.014 |
| [2] |
Allen, D.E. Limit states design[DB/OL]. Canadian Building Digest, 1982-01-01. https://doi.org/10.4224/40000759.
|
| [3] |
Das B.M.. Principles of geotechnical engineering[M]. Cengage learning, 2020.
|
| [4] |
Otani S. Earthquake resistant design of reinforced concrete buildings[J]. Journal of Advanced Concrete Technology, 2004, 2(1): 3-24. DOI:10.3151/jact.2.3 |
| [5] |
周景星, 李广信, 张建红, 等. 基础工程[M]. 清华大学出版社, 2015.
|
| [6] |
AISC, 1986. Load and resistance factor design[M]. In: Manual of Steel Construction. American Institute of Steel Construction, Chicago.
|
| [7] |
中华人民共和国住房和城乡建设部. 钢结构设计标准: GB 50017-2017[S]. 北京: 中国建筑工业出版社, 2017.
|
| [8] |
中华人民共和国交通运输部. 公路桥涵地基与基础设计规范: JTG 3363-2019[S]. 北京: 人民交通出版社, 2019,
|
| [9] |
李广信, 张丙印, 于玉贞. 土力学[M]. 2版. 北京: 清华大学出版社, 2013.
|
| [10] |
中华人民共和国住房和城乡建设部. 建筑地基基础设计规范: GB 50007-2011[S]. 北京: 中国计划出版社, 2012.
|
| [11] |
de Beer E E. Experimental determination of the shape factors and the bearing capacity factors of sand[J]. Géotechnique, 1970, 20(4): 387-411. DOI:10.1680/geot.1970.20.4.387 |
| [12] |
Hansen J.B. A revised and extended formula for bearing capacity[J]. Danish Geotechnical Institute, Bulletin No. 28, Copenhagen. 1970.
|
| [13] |
Meyerhof G G. Some recent research on the bearing capacity of foundations[J]. Canadian Geotechnical Journal, 1963, 1(1): 16-26. DOI:10.1139/t63-003 |
| [14] |
Meyerhof G.G. The bearing capacity of foundations under eccentric and inclined loads[C]. Proc. of the 3rd Int. Conf. on SMFE. 1953, 1: 440-445.
|
| [15] |
Vesi A S. Analysis of ultimate loads of shallow foundations[J]. Journal of the Soil Mechanics and Foundations Division, 1973, 99(1): 45-73. DOI:10.1061/JSFEAQ.0001846 |
| [16] |
中华人民共和国住房和城乡建设部. 建筑桩基技术规范(JGJ94-2008)[S]. 中国建筑工业出版社, 2008.
|
| [17] |
Das B.M., Sivakugan N. Principles of foundation engineering[M]. Cengage learning, 2017.
|
 2021, Vol. 30
2021, Vol. 30

