“一带一路”国家战略倡议自2013年实施至今,我国同沿线国家在城市基础设施建设方面开展了大量合作,为新时代城市化建设提供了众多有益范本,对国内高校的专业升级产生了重要影响。
2016年6月2日,中国正式成为《华盛顿协议》缔约国,在打开中国工程教育毕业生走向国际人才市场大门的同时,也考量了中国工程教育毕业生的综合能力[1]。世界各国越来越重视实业生产和新经济、新业态、新技术的发展。现阶段,强调对具有创新创业能力和跨界整合能力的新型工程科技人才培养,成为高等院校对传统工科专业升级以及工程教育创新的重要使命。
面对新一轮科技革命和产业变革,新经济潮对传统工科产生了巨大冲击,我国以教育部领衔的“复旦共识”“天大行动”和“北京指南”应运而生[2-3]。新工科背景下,城市地下空间工程专业发展迎来了重大机遇,同时也将面临教学改革方面的挑战。
南京作为“一带一路”国家战略交汇点的重要枢纽城市,正努力提升与首位度相匹配的城市能级,以国际化的理念推进城市发展,在对老城有机更新和新城建设的同时,不断探索城市地下空间工程建设的科学发展。
南京工业大学聚焦于国内一流、国际知名创业型大学的办学定位,其城市地下空间工程专业是江苏省首开、全国首批土木工程大类的特色专业,于2019年评选为教育部全国城市地下空间工程专业教学指导组副组长单位,并于2020年度入选国家级一流本科专业建设点,是新工科背景下学校学科建设的重点专业。
南京工业大学城市地下空间工程专业面向城市地下空间开发利用的全产业链,立足学校完备的学科布局,构建融合城市规划、地质工程、土木工程和交通工程等多学科交叉的人才培养模式;面向数字孪生城市,依托产学研融合平台,协同行业标杆企业,构建以虚拟仿真、创新训练、工程实践为特色的实践教学体系。
土力学作为城市地下空间工程专业核心课程。在各高校的课堂教学中,现阶段仍较多采用年代久远且离学生实际生活较远的工程案例,如1913年的加拿大特朗斯康谷仓地基失稳、意大利比萨斜塔、墨西哥城的地基沉降等。此类经典工程案例虽然能够作为土力学的教学素材,但却是传统土木工程专业中普遍沿用至今的案例。既没有考虑到城市地下空间工程的专业性,也没有结合新时代中国新基建特色,无法体现教学内容的前沿性和时代性,在教学过程中难以与学生产生很好的专业共鸣。如何在土力学教学中,结合城市地下空间工程专业特点,让学生有针对性地掌握知识点,并能将其应用于城市地下空间的开发建设,是专业课教学中急需解决的问题。因此,新工科背景下,面向城市地下空间工程专业的土力学案例教学探索显得尤为重要且迫在眉睫[5]。
一、新工科背景下土力学案例教学探索 (一) 教学案例引入南京作为华东地区及长三角地区的唯一特大城市,肩负着“一带一路”国家战略、长江经济带和长三角一体化枢纽城市的重要使命。在新型城镇化建设的过程中,南京市江北新区中央商务区地下空间项目作为新时代背景下的新基建工程,是新工科背景下的典型案例。
南京市江北新区中央商务区地下空间项目位于国家级南京市江北新区的核心区域,其地下空间剖面示意图如图 1所示。地下空间总占地面积约62 hm2,最大挖深约48 m。项目总建筑面积约148万m2,主要内容包括地下停车场约55万m2,地下配建商业约24万m2,两个3线换乘轨道交通站厅及区间约5.14万m2,综合管廊、地下环路及其他市政设施约18.7万m2,附属设备约29.9 m2等。该项目为国内现阶段建设规模最大、集成度最高的城市地下空间。

|
图 1 南京市江北新区中央商务区地下空间项目剖面示意图 |
该项目基坑距离长江最近处仅仅700 m,地下水位平均埋深仅1.35 m,近江平均挖深约40 m,最大开挖深度达48 m,地下连续墙平均深度达72 m。地勘报告显示,场地主要为粉质黏土、淤泥质粉质黏土、夹薄层的粉土、粉砂等。为实现施工阶段的挡土结构物与地下空间投运后的主体结构复合设计,该项目在最深基坑处设计采用800 mm的地下连续墙,如图 2所示。

|
图 2 地下连续墙现场实景照片 |
基坑工程历来被认为是实践性很强的岩土工程问题,是土力学中的重要课题,同时基坑工程又极具时代性。随着城市地下空间的大力开发,基坑规模越来越大,开挖越来越深,周围建筑越来越密集,地质条件以及周边情况越来越复杂,基坑工程已变成一个综合性的岩土工程问题。
南京市江北新区中央商务区地下空间项目,城市规划定位高、城市要素高度集成、地质水文复杂多变、岩土结构设计困难等,是新工科背景下城市地下空间工程专业土力学课程案例探索的最佳选择。该工程案例的基坑设计和施工涵盖了经典土力学中的强度、变形、渗流三大问题。
强度问题主要体现在地下连续墙设计过程中,土压力的计算、稳定性验算等;变形问题主要体现在开挖过程中,基坑底部回弹、维护结构后的地表沉降等;渗流问题主要体现在基坑降水产生的基坑内外水头差,从而引起的潜在管涌风险等,都与土力学的教学内容息息相关。本文以土压力理论为例对其进行教学探索,以期实现激发学生学习积极性,实现为高校毕业生实际工作能力提升奠定良好实践基础的目的。
(二)朗肯土压力计算理论土体的强度是土力学中三大主要问题之一,土压力计算是其主要知识点,是土力学专业课程中的重点授课内容[5]。土压力根据墙体位移条件可以分为静止土压力、主动土压力和被动土压力。
朗肯土压力理论是依据半空间体的应力状态和土的极限平衡理论推出土压力强度的计算方法,它的基本假定为墙背直立、光滑,墙后填土面水平。
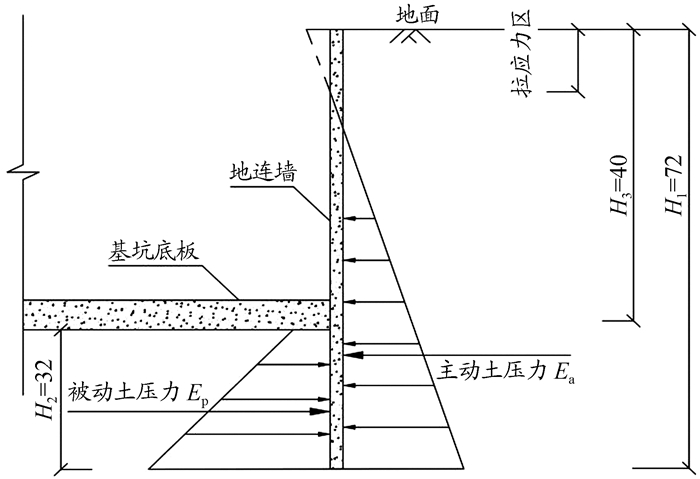
将上述工程案例简化为典型的土压力计算模型,如图 3所示。若挡土墙发生离开填土方向移动,直到墙后填土达到极限平衡状态时,作用在挡土墙上的土压力即为主动土压力。根据土的极限平衡条件,地面以下任一深度z处的主动土压力强度σa为:
| $ {\sigma _{\rm{a}}} = \gamma z{K_{\rm{a}}}{\rm{ - }}2c{\rm{ }}\sqrt {{K_{\rm{a}}}} $ | (1) |
|
图 3 土压力计算模型图 |
式中,Ka——朗肯主动土压力系数
Ka=tan2(45°-ϕ/2)
γ——土的重度;
c——土的黏聚力;
ϕ——土的内摩擦角。
由式(1)可知,主动土压力由两部分组成:一是由土自重引起的压力,二是由黏聚力引起的拉力。黏聚力的存在减少了作用在墙上的土压力,并且在墙上部形成一个负侧压力区(拉应力区)。由于土体不能承受拉力,令σa=0,就可等到填土受拉区的最大深度z0为:
| $ {z_0} = \frac{{2c}}{{\gamma \sqrt {{K_a}} }} $ | (2) |
则作用在单位长度挡土墙上总的主动土压力Ea为:
| $ {E_{\rm{a}}} = \frac{1}{2}\gamma {\left( {{H_1} - {z_0}} \right)^2}{K_{\rm{a}}} $ | (3) |
式中,H1——地下连续墙高度。
若挡土墙发生向填土方向移动,直到墙后填土达到极限平衡状态时,作用在挡土墙上的土压力即为被动土压力。根据土的极限平衡条件,地面以下任一深度z处的被动土压力强度σp为:
| $ {\sigma _{\rm{p}}} = \gamma z{K_{\rm{p}}} + 2c\sqrt {{K_{\rm{p}}}} $ | (4) |
式中,Kp——朗肯被动土压力系数
| $ {K_{\rm{p}}} = {\rm{ta}}{{\rm{n}}^2}({45^\circ } + \phi /2) $ |
黏聚力的存在增加了被动土压力,则作用在单位长度挡土墙上总的被动土压力Ep为:
| $ {E_{\rm{p}}} = \frac{1}{2}\gamma H_2^2{K_{\rm{p}}} + 2c{H_2}\sqrt {{K_p}} $ | (5) |
式中,H2——基坑底板以下地下连续墙高度。
(三)有均布荷载的土压力计算在地下连续墙施工阶段,需要考虑地面的工作荷载对土压力计算的影响,通常取为均布荷载。
若填土表面上有均布荷载q时,则地面以下任一深度z处的主动土压力强度σa为:
| $ {\sigma _{\rm{a}}} = {\gamma _z}{K_{\rm{a}}} + q{K_{\rm{a}}} - 2c\sqrt {{K_{\rm{a}}}} $ | (6) |
此时,拉应力区最大深度z0为:
| $ {z_0} = \frac{{2c}}{{\gamma \sqrt {{K_{\rm{a}}}} }}{\rm{ - }}\frac{q}{\gamma } $ | (7) |
当式(7)中z0>0时,在z0深度内填土中将产生拉裂缝而使土压力为0,则单位长度挡土墙上总的主动土压力Ea为:
| $ {E_{\rm{a}}} = \frac{1}{2}\gamma {\left( {{H_1} - {z_0}} \right)^2}{K_{{\rm{a}}}} $ | (8) |
当式(7)中z0<0时,填土中不会出现拉应力区,则总的主动土压力Ea为:
| $ {E_{\rm{a}}} = \frac{1}{2}\gamma {H_1}^2{K_{\rm{a}}} + q{H_1}{K_{\rm{a}}} - 2c{H_1}\sqrt {{K_{\rm{a}}}} $ | (9) |
若填土表面上有均布荷载q时,则地面以下任一深度z处的被动土压力强度σp为:
| $ {\sigma _{\rm{p}}} = \left( {{\gamma _z} + q} \right){K_{\rm{p}}} + 2c\sqrt {{K_{\rm{p}}}} $ | (10) |
则作用在单位长度挡土墙上总的被动土压力Ep为:
| $ {E_{\rm{p}}} = \frac{1}{2}\gamma {H_2^2}{K_{\rm{p}}} + qH{K_{\rm{p}}} + 2c{H_2}\sqrt {{K_{\rm{p}}}} $ | (11) |
南京市江北新区中央商务区,场地土层条件复杂,并非理想化的单一土层。在地下连续墙的工程设计中,土压力的计算应考虑土层性质的不同(重度γ、黏聚力c、摩擦角ϕ)对土压力的影响。
在计算成层土的土压力时,需注意两点:一是由于各土层的重度γ不同,土压力分布会在土层分界面处出现转折;二是由于各土层的黏聚力c和摩擦角ϕ,所以主动土压力系数Ka和被动土压力系数Kp不同,在计算各土层土压力时,需采用对应的黏聚力c和摩擦角ϕ。
二、基于“两性一度”标准下的教学案例研讨土力学问题的复杂性和不确定性一半以上都源于水[6]。南京市江北新区中央商务区场地地下水位平均埋深仅1.35 m,在计算土压力时,必须考虑地下水位以下土体由于水的浮力作用,有效重度的减轻引起土压力减小的问题。因此,地下水位以下的土体在计算土压力时必须采用浮重度γ′计算。作用在地下连续墙的土压力还应包括水压力的作用,即地下连续墙上的总压力包含了土压力和水压力两部分。
南京市江北新区中央商务区地下空间工程项目,其地质条件复杂。地下连续墙后的土层既有弱透水性的淤泥质粉质黏土,又有强透水性的含卵石砾砂,更有几乎不透水的泥质砂岩。如表 1所示,作用于地下连续墙上的总压力究竟应该采用水土分算还是水土合算,要根据其适用的工况来确定[7]。
| 表 1 土层参数表 |
现阶段,对于砂性粉土、砂土和碎石土等强透水性土质,其土体颗粒是碎散的,孔隙水水力贯通。基于有效应力原理,宜采用水土分算法[7-8]。对此,无论是学术界还是工程界均取得共识。
对于粉质黏土、黏性土等弱透水性的土体,其土颗粒表面存在结合水,土体孔隙中的水并非完全水力贯通。若按静水压力模式计算土压力体系中的孔隙水压力的结果并不准确,所以采用水土分算并不适宜,采用水土合算更为合理[7-9]。同样对于岩石类特殊的不透水介质,采用水土分算也并不适宜。虽然现阶段对于弱透水性土体和岩石类特殊土体,其土压力计算在学术界并无统一意见,但在实际工程应用中,常采用水土分算的方式计算此类土体的土压力。
引入南京市江北新区中央商务区地下空间项目作为教学案例,很好地体现了新工科背景下的时代性和创新性。通过开展土水分算合算问题的讨论,引导学生运用所学的土力学知识解决复杂工程问题,更提升了课程的高阶性和挑战度。
三、案例教学实施在课堂教学中,选取具有较强视觉冲击力的视频、图片等素材,生动形象地展示南京市江北新区中央商务区地下空间项目,能够增强学生对地城市地下空间工程的感性认知,激发学生的学习兴趣。通过案例引入开展朗肯土压力计算理论的教学,将实际工程案例简化为经典的土压力计算理论模型,使学生对土压力的理解不再只是停留在表面,而是能够真正将其应用到实际的地下空间工程中。考虑到实际场地土层条件的复杂性,以及在地下连续墙施工阶段地面工作荷载的影响,讲解成层土和有均布荷载的土压力计算方法,逐步培养学生解决复杂问题的综合能力和高阶思维。
在“土水分算合算”研讨课程设计中,在学生掌握了相关土压力知识点的基础上,组织学生针对水—土压力的计算究竟应采用水土分算还是合算,以及各自的适用工况等问题开展研讨,引导学生从已经学过的有效应力原理和不同三轴试验间的内在联系进行深入思考分析,提升课程的挑战度。
在课程考核中,为了能够较好的评价课程教学效果和学生的学习效果,针对案例教学中各环节设计相应评价指标及权重值,加强学习过程的评价考核权重,减少期末考试成绩的占比,对学生的理论基础知识掌握情况、分析解决问题的能力、自主学习能力、创新能力等方面进行综合考察评价。
四、结语新工科背景下城市地下空间工程专业的培养目标,必须突出学生理论联系实际的能力。土力学是城市地下空间工程专业重要的专业课程,也是一门理论性、经验性和实用性很强的学科,因此其教学案例更应立足于与学生息息相关的实际工程实践中。
在教授基本理论知识的同时,也应注重拓展学生专业思维。如对于挡土结构物后的黏性土,在现阶段的学术界或工程界并未形成共识的水土分算合算问题,针对本文所举案例项目的复杂地层条件拓展性研究水土合算或水土分算的适用性,充分调动学生专业课程学习兴趣,引发其专业共鸣,同时能够使学生迅速适应工程实际需求,掌握完备的理论基础和提升专业思维能力。
| [1] |
袁立群, 崔诗才, 赵庆双. 新工科背景下土力学案例教学研究[J]. 高等建筑教育, 2019, 28(2): 61-65. |
| [2] |
胡波, 冯辉, 韩伟力, 等. 加快新工科建设, 推进工程教育改革创新——"综合性高校工程教育发展战略研讨会"综述[J]. 复旦教育论坛, 2017, 15(2): 20-27. DOI:10.3969/j.issn.1672-0059.2017.02.004 |
| [3] |
"新工科"建设复旦共识[J]. 高等工程教育研究, 2017, 162(1): 10-11.
|
| [4] |
王璐, 沈扬, 刘云, 等. "新工科"视角下土木类大学生学习共同体构建[J]. 高等建筑教育, 2020, 29(4): 1-7. |
| [5] |
陈国兴, 樊良本, 陈甦, 等. 土质学与土力学[M]. 2版. 北京: 中国水利水电出版社, 2006.
|
| [6] |
沈扬. 土力学原理十记[M]. 北京: 中国建筑工业出版社, 2015.
|
| [7] |
王钊, 邹维列, 李广信. 挡土结构上的土压力和水压力[J]. 岩土力学, 2003, 24(2): 146-150. DOI:10.3969/j.issn.1000-7598.2003.02.002 |
| [8] |
李广信. 基坑中土的应力路径与强度指标以及关于水的一些问题[J]. 岩石力学与工程学报, 2012, 31(11): 2269-2275. DOI:10.3969/j.issn.1000-6915.2012.11.015 |
| [9] |
高彦斌, 姚天骄, 杨正园. 饱和黏性土的总强度与基坑工程水土合算土压力分析方法[J]. 同济大学学报(自然科学版), 2020, 48(9): 1296-1304. |
 2021, Vol. 30
2021, Vol. 30

