本科生课堂教学是本科教育的核心环节。多年以来,教育主管部门、高等院校和高校教师对本科生课程教学给予了高度重视,开展了大量教学研究工作。工科类专业的本科课程设置主要包括基础课(公共课)、专业基础课和专业课。对基础课和专业基础课的教学研究较为深入系统,而对专业课的教学研究则相对薄弱。由于专业课种类繁多,又各具特点,对专业课课堂教学的共性问题研讨尚显薄弱。事实上,在整个本科教学体系之中,专业课程占总课程门数的60%以上,而课时则占总学时的40%,甚至50%以上。与此形成鲜明对比的是,对工科类专业的本科专业课课堂教学共性问题的教学研讨寥寥无几。因此,以土木工程专业课课堂教学实践为基础,提出共性与具体、科学与常识、定性与定量“三结合”的教学理念,即在课堂教学中注重科学共性基础与具体问题相结合、科学原理与生产生活经验常识相结合、定性与定量相结合。
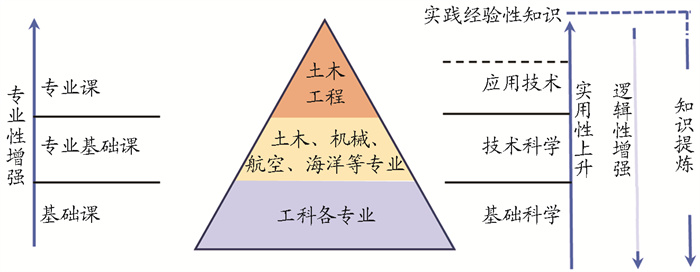
一、工科类专业本科生课程体系设置与钱学森现代科学技术体系观在工科本科生课程体系中,主要包括基础课、专业基础课和专业课。对土木工程本科生而言,基础课包括高等数学、普通物理学等课程,这些课程也是绝大部分工科专业学生要学习的课程。土木工程专业基础课包括理论力学、材料力学、结构力学等课程,有些也是机械工程、航空航天工程、港口、水利和海洋工程等多个学科的专业基础课。专业课则包括荷载与结构设计、钢结构、钢筋混凝土结构等课程。从基础课、专业基础课到专业课,专门化程度上升、参与学习的人数逐步由整个工科到部分工科专业再缩小为土木工程专业。从专业及学习的人数来看,从下到上呈金字塔形(图 1)。从基础课到专业课的知识实用性上升,但与此同时其适用范围减小、逻辑性减弱。钱学森先生将现代科学技术体系划分为11个门类,同时,在每个门类中又分为基础科学、技术科学与工程技术3个层次[1]。不难看到,工科类专业的大学本科基础课、专业基础课和专业课的设置,与基础科学、技术科学和应用技术3个层次的划分具有内在一致性。
|
图 1 土木工程专业本科知识体系及其逻辑性示意图 |
从经验性知识到应用技术、技术科学与基础科学的过程是从感性认识向理性认识提升和飞跃的过程[2]。与实践经验性知识相比,专业课知识具有一定的科学基础与逻辑体系,但与专业基础课和基础课相比,专业课知识经验性相对较强,逻辑性相对较弱。学生在大学一、二年级基本学完基础课和专业基础课,建立起对现代科学逻辑严密性、定量精确性和体系完整性的印象,开始接触专业课后,有逻辑体系不再、精确性“瞬间崩塌”、内容“零碎杂糅”之感,而且,似乎感觉基础课和专业基础课所学知识在专业课中的应用很少。这一强烈的反差,是造成不少本科生感觉专业课学习难以深入,对专业课学习兴趣下降的重要原因。
基础课知识是经简化、提炼和抽象后积淀下来的逻辑严密的科学知识。例如,一般工科本科生在高等数学中学习的知识体系,在150年前已经基本成型,即使线性代数与概率论中的知识,也已经有80年以上的历史[3]。数学家希尔伯特指出,经过逻辑梳理的知识体系和理论工具,虽然在某种意义上变得更为抽象,但本质上更简单、更强大[4-5]。逻辑体系不具跳跃性,一步一个阶梯,因此,学习具有逻辑体系的知识在本质上更为容易。这可能是为什么近代以来的学校教育,无论在小学、中学和大学,都以逻辑化的知识教育为第一要务的根本原因。反之,在本科专业课中学习的知识,则往往历史相对较短,且由于实际问题的复杂性而难以对每个环节进行逻辑严密的科学处理,在本科课程中通常仅给出最终的简化结果。工程实际问题总体上较零碎,跳跃性较大,逻辑体系不严整。事实上,随着科学技术的发展,人们不断从实践经验性知识中提取科学认识,夯实科学基础,对应用技术、技术科学乃至基础科学进行更新和完善[1, 6],这是一个不断发展、永无止境的动态过程。专业课相当于“技术科学”与“应用技术”的衔接,或“应用技术”为主,即使随着时间的推移和科技水平的提高,专业课的相关知识得到更新和完善,与基础课相比,其逻辑性相对较弱的基本格局也不会随着时间的推移而得到根本改变。
二、本科生专业课程课堂教学的“三结合”在本科生专业课的课堂教学中应体现共性与具体、科学与常识、定性与定量三结合的教学理念,即科学共性基础与具体问题相结合、科学原理与生产生活经验常识相结合、定性与定量相结合,使学生既能把握总体的逻辑体系、掌握知识要点,又能逐步学习和领会对工程实际应用和决策来说至关重要的一些基本原则。
(一)科学共性基础与具体问题相结合现代工程技术虽然难免具有经验性知识与成分,有时甚至比重还较大,但是,科学共性原理在工程分析、设计与决策中占有基础性地位[6],则是现代工程技术与以经验为主的古代工程技术的根本性差别。因此,结合专业课中的具体知识点强调科学共性基础与具体问题相结合的重要性,由此建立专业课不同知识点之间的内在逻辑联系至关重要。
以土木工程专业课荷载与可靠性设计原则为例,在风荷载和地震作用两部分,分别介绍风的基本知识和地震基本知识,其中风的分级表和地震烈度表是重要的基本知识。事实上,人们对具体现象进行科学认识的第一步,即从感性认识迈向理性认识的第一步,往往是对纷繁芜杂的经验知识进行初步整理,给出合理的分类,因此,在讲课中,应强调科学分类这一科学认识过程的统一性。例如,对于风级,无论是唐代科学家李淳风将风的等级根据树木响应的情况分为“动叶、鸣条、摇枝、堕叶、折小枝、折大枝、折木飞砂石、拔大树和根”等八级风力标准[7],还是“蒲氏风级”中以“静、烟直上”,即“大漠孤烟直”景象为特征的“静风”,或以“渔船满帆时倾于一方”,即“风正一帆悬”的“和风”,以及“微枝折毁”的“大风”和“陆上少见,见时可使树木拔起或建筑物摧毁”的“狂风”等12级标准[8],在早期无法进行定量观测的情况下,都是以人们可见可感的海洋或陆地地面物征象作为科学划分的第一标准。类似地,在中国地震烈度表中,对于6度以下的情况,也主要以诸如“惊慌失措,仓皇逃出”等人的感受和“不稳定物翻倒”等物理现象区分。从这里,不难看到古今中外的科学家在风级和地震烈度研究科学方法上的共同之处。事实上,跨出从经验到科学认识的这一步,即科学分类,虽然难免具有经验性和模糊性,但却意味着人们开始对基本现象进行系统化梳理与逻辑归类[2],因而开始触及科学的脉搏,乃是真正科学研究,即理性认识的开始。
又如,在介绍动水压力和风压力的过程中,都需要用到伯努利公式,即对于层流中的一根流线,其“动”压强和“静”压强之和为常数。这一原理,从本质上解释了动水压力与水的密度成正比、与流速平方成正比,风压力与空气密度成正比、与风速(气流速度)平方成正比这两个事实在科学原理上的统一性。尽管在教材中[8],这一基本原理的推导是在风压部分(在水压力之后)进行的,但在讲到动水压力时可进行一个更为简洁的推导。事实上,只需要两个关键公式就可以解决问题:考察一维稳定层流的流线所在的微小直线流管(不是水管的管道),记横轴方向空间坐标为x,以向右为正,微团长度为dx。设截面积为A,流体微团的速度为v。显然,速度v和流体压强p本质上是x和t的函数。对于稳定层流,在给定空间点的“视”速度不随时间变化,即
| $ \partial v\left( {x, t} \right)/\partial t = 0 $ |
与此同时,该流体微团左侧的压力为p(x, t)A,右侧的压力为p(x+dx, t)A。因此,根据牛顿第二定律,有
| $ \rho A{\rm{d}}x{\rm{d}}v(x, t)/{\rm{d}}t{\rm{ }} = [p(x, t) - {\rm{ }}p(x{\rm{ }} + {\rm{d}}x, t)]A $ |
式中,dv(x, t)/dt为流体微团的加速度,是一个全微分。这是第一个关键公式。从中消去A,并对右侧利用一阶Taylor展开,可得
| $ \rho {\rm{d}}v\left( {x, t} \right)/{\rm{d}}t + \partial p/\partial x = 0 $ |
对于流体微团来说,其所在位置也与时间有关,即
| $ {\rm{d}}v(x, t)/{\rm{d}}t{\rm{ }} = \partial v(x, t)/\partial t + v\partial v/\partial x $ |
由于
| $ \rho v\partial v/\partial x + \partial p/\partial x = 0 $ |
这是第二个关键公式。由此积分即可得到ρv2/2+p=C,C为积分常数。此即著名的伯努利公式[9],这一公式对层流流体(无论气体还是液体)均成立。在这一推导过程中,同时复习了高等数学中的全微分概念、Taylor展开和链式法则,从而认识到基础课所学知识(科学共性基础)是如何融会贯通地应用到具体工程问题中的。通过这一概念,避免了欧拉描述、拉格朗日描述、当地速度、对流影响等本科生不易理解的概念。
与此相反,虽然同为流体,但在风对结构的作用与波浪对结构作用的计算中,基本公式却不同。在风对结构的作用中,顺风向风压是CDρav2/2,其原理来自伯努利公式,CD是一个比例系数,ρa是空气密度。而在波浪对小直径圆柱形物体的计算中,则可采用Morison公式
| $ C{\prime _D}D{\rho _w}v{\rm{ }}\left| {{\rm{ }}v{\rm{ }}} \right|{\rm{ }}/2 + {\rm{ }}C{\prime _{acc}}{\rho _w}\pi {D^2}\dot v{\rm{ }}/4 $ |
其中,D是圆柱体直径,C′D,C′acc为通过实验确定的系数,ρw为水的密度。该式中第一项是黏性作用项(与速度有关),第二项是与惯性力有关的项,ρwπD2/4是单位长度圆柱体大小的水的质量,而
科学共性原理的统一性往往体现为科学规律(如物理或力学规律)及其数学公式表达的一致性。不少学生对数学公式表现出某种天然的畏惧。在具体讲课过程中,让学生意识到数学公式是表达科学规律的精确语言和强大工具,从而消除学生的畏惧感,增强基于科学共性原理、利用这一工具精确表达和解决具体工程问题的信心。
(二)科学原理与生产生活经验常识相结合在专业课中,来自生产生活经验常识的知识较多。拘泥于生产生活经验常识可能导致创造性的禁锢,甚至错误的直觉判断。然而,科学原理与生产生活经验常识并非总是相悖的,相反,在大部分情况下具有一致性。事实上,科学原理与生产生活经验常识是对立统一的。人们根据生产经验常识而对问题产生误判的情况,一般是对基本条件的认识不清晰或对存在复杂非线性耦合效应的系统进行“线性外推”的结果[10]。例如,亚里士多德没有认识到对轻质物体(如羽毛)来说空气作用力不可忽略,因而得出了错误的落体运动规律。与基础课教学相比,在专业课课堂教学中,科学原理与生产生活经验常识的结合尤为重要,可帮助学生逐步建立工程直觉。
例如,在课程中,涉及楼面活荷载的取值。在规范中给出的楼面活荷载取值,是通过经验或实际数据、采用概率统计并加以适当工程判断的结果[11]。在这里,符合客观实际与概率统计分析是处理这一问题的科学原则。对于活荷载的处理,有两个要点:第一,从历史上看,在不同时期修订的规范中活荷载取值一般是增大的。以桥梁为例,近30年,车流密度增大,因而活荷载必然增大,这一经验常识就是前述荷载设计取值增大的基本背景。第二,活荷载的取值依据与使用情况及物理背景有关。例如,对于普通住房的楼面活荷载,我国现行规范的取值为2.0 kN/m2。这一数值对于一般的学生来说没有直观概念。事实上,在一个房间的楼面上若每平方米上站3个人,每人平均体重70 kg,则其重力密度约2.0 kN/m2。上述人员布局情况虽然稍显极端,但在家庭聚会时可能局部楼面会接近这一极端状态,考虑到设计荷载取值一般偏大,作为设计取值标准是具有合理性的。将上述设计取值与日常经验常识结合,有助于逐步建立工程直觉。
又如,在侧压力和地震作用部分,都涉及波动,需要介绍一些波的基本性质。但由于课时有限,不可能通过详细的波动方程推导介绍这些基本概念。因此,结合生产生活常识直观地说明有关概念,是学生比较容易接受的方式。首先,波动分为体波和面波,即在物体内部传播的波和仅在表面附近存在和传播的波。例如,海洋表面上可能惊涛骇浪,而一定深度以下则十分平静。不仅是水面,地球表面也存在类似情形。体波又分为纵波和横波。固体中可以传播纵波和横波,但静止流体,不能承受剪应力,横波是剪切波,不能在流体中传播。固体中的波传播速度比流体中的波速大。沈括在《梦溪笔谈》中记载:“古法以牛革为矢服,卧则以为枕。取其中虚,附地枕之,数里内有人马声,则皆闻之。”就是利用了这一性质。波速又和很多因素有关,不仅在不同介质中不同,在同一介质中不同类型波的波速也不同,而且可能与波长等有关。例如,在平静的湖面上丢入一个石头产生的涟漪,一秒钟只传播数米;但1960年智利大地震引起的海啸,以每小时800 km(约220 m/s)的速度,横穿太平洋,24 h后袭击了日本海岸。可见水波波速可以从每秒几米到每秒200多米,不仅与介质的性质有关,还与波长(或频率)有关,即存在散射现象。波浪还有浅水波和深水波的差别。浅水波的波速与水深有关,浅水波的波速为
通过上述生产生活经验中关于波动现象的常识与物理规律加以解释,有助于学生对相关知识的深入理解。
(三)定性与定量相结合定性与定量相结合,是基于科学基础、解决具体复杂工程问题的不二法门[10, 13]。现代计算机技术与装备的发展,为定量计算与分析提供了强大的工具。然而,定量计算的基础是正确的科学理论与合理的工程模型。对定量计算结果的判断与检验,随着现代分析工具和方法的发展而愈益重要[14]。在专业课的课程教学中,关于定性与定量相结合的例子俯拾皆是。
例如,前述列举的浅水波与深水波的概念,关于“深”“浅”,是定性的区别,这是由于浅水波与深水波有一系列性质上的差别。然而,何为“深”,何为“浅”?并非简单地根据绝对水深而论。根据波动理论,当水深小于波长的1/2时,为浅水波,否则为深水波。因此,以大海之深,可有浅水波,以池塘之浅,可载深水波。由此可见,“深、浅”水波的分类依据是水深与波长之比。类似地,对小圆柱物体,可以采用Morison公式计算波浪作用力。当物体的尺度较大时,可以采用直墙上的波浪作用方法计算。介于其间的第二类问题,则需要根据绕射理论具体分析。大体上说,海上的灯塔一般属于第一类,海边的防波堤一般属于第三类,而大型浮体,如大型货船或航母,则可能属于第二类。对于不同的分类,需要分别采用不同的定量方法分析。然而,这3种定性分类本身,并非简单地以人的感觉为依据,而是通过波长与物体尺度之比这一定量指标来划分,即波长与物体线度之比小于0.2、介于0.2~1.0和大于1.0时,分别为上述三类。因此,从科学上看,并非肉眼直观所见的水中之墙都是“直墙”,而是从定量上满足波长与长度之比大于1的构筑物方为波浪力计算中定义的科学意义上的“直墙”。
又如,在波浪力计算中,有一个高度差定义为“波浪中线(平分波高的中线)与计算水平面(即平均水平面或静水面)之差”。如何理解二者之差?涉及线性波与非线性波的定性差别。“风乍起,吹皱一池春水”,一般由此产生的波是微小的波,类似于对称波纹(正弦形状),基本是上下对称的,这时波浪中线与计算水平面是重合的,二者之差为零。“大雨落幽燕,白浪滔天”,这时的波浪,已经接近或发生破碎,其形状波峰尖、波谷缓,正如在海边沙滩常见的波浪那样。这时的波浪为非线性波浪,显然,此时计算水平面较波浪中线要低。由此可见,在分析中考虑波浪中线与计算水平面之差,在某种程度上考虑了非线性波浪影响。线性波浪与非线性波浪是定性不同的两种情况,如何区分?可以用波陡,也就是浪高与波长之比来定量划分。对于深水波,当波陡大于5%时,一般非线性效应开始变得显著,而波陡达到10%时波浪开始破碎。
在土的侧压力计算中,根据挡土墙是否移动及如何移动,有静止土压力、主动土压力、被动土压力之别。一般学生容易记反主动土压力与被动土压力的定性特性。实际上,可以直观理解为“主动土”压力和“被动土”压力。“主动土”压力是指土“主动地”发生变形并产生对挡土墙的压力,这是由于挡土墙具有离土体而去的位移。“被动土”压力是由于挡土墙要向土体方向移动,因而土体“被动地”受到外来的压力。如此一来,就容易理解“主动土”压力一定小于静止土压力,而“被动土”压力一定大于静止土压力。在这一定性认识的基础上,采用Rankine土压力理论,结合Mohr应力圆上土应力状态点的移动,很容易根据图解进一步计算出“主动土”压力和“被动土”压力大小。
在工程实践中,根据工程经验给出某些物理或力学量的数量级估计是非常重要的[13]。例如,在总高632 m的上海中心大厦开始规划之初,基本方案尚未确定,只有总尺寸、总高度和总层数的基本设想,判断地基是否能承载,需要多少根桩,就需要估计总重量。在重力荷载一节中,给出了混凝土结构折算到每层单位面积重量的基本数值[5],对钢筋混凝土结构,折算的每层单位面积平均重量为4.95~7.43 kN/m2。混凝土的容重约为24 kN/m3,将包括楼板、墙、柱等混凝土总重量平铺折算为混凝土楼板时,其等效厚度约为0.2~0.3 m。对于上海中心大厦,按照130层估算,其总折算等效厚度为26~39 m。对于上海中心大厦这样的超高层建筑,一般设计安全性要求较高、用材较多,且层数越多,中下部柱和墙的截面积相对楼板面积比例越大,因而折算重量越大,底部折算重量可以考虑1.5~2.0的放大因子。以平均每层面积70 m×70 m估计,130层总重量为46~92万t,中值约为69万t。这一估计值与实际重量74.8万t在同一数量级上[15]。可见,即使根据工程经验进行粗略的定量估计,在设计中特别是规划阶段,也对工程决策起到重要作用。
三、结语工科类本科专业课程教学起着连接大学基础教育与工程实践教育的桥梁作用,具有至关重要的地位。因此,文章梳理了工科类专业的本科课程体系与钱学森现代科学技术体系观之间的对应关系,论述了专业课程教学的逻辑地位,在本科专业课程教学中应体现科学共性基础与具体问题相结合、科学原理与生产生活常识经验相结合、定性与定量相结合的教学理念,并通过具体教学实践进行了阐述。共性与具体、科学与常识、定性与定量相结合的三项基本原则,不仅是处理工程技术问题的重要方法,也是哲学基本原理在本科生专业课中的具体体现。在教学过程中,上述三个方面不是完全分开的,在一个具体问题中可能同时体现了其中的两个甚至三个方面。
| [1] |
顾孟潮. 钱学森论建筑科学[M]. 2版. 北京: 中国建筑工业出版社, 2014.
|
| [2] |
毛泽东. 毛泽东选集(第一卷)[M]. 2版. 北京: 人民出版社, 1991.
|
| [3] |
M.克莱因. 古今数学思想[M]. 上海: 上海科学技术出版社, 2009.
|
| [4] |
希尔伯特. 数学问题[M]. 李文林, 袁向东, 译. 大连: 大连理工大学出版社, 2014.
|
| [5] |
陈建兵. 研究生课程中教师应起到怎样的作用?[J]. 高等工程教育研究, 2015(4): 116-120. |
| [6] |
钱学森. 工程和工程科学[J]. 力学进展, 2009, 39(6): 643-649. |
| [7] |
陈美东. 中国科学技术史[M]. 北京: 科学出版社, 2003.
|
| [8] |
李国强, 黄宏伟, 吴迅, 等. 工程结构荷载与可靠度设计原理[M]. 4版. 北京: 中国建筑工业出版社, 2016.
|
| [9] |
欧特尔. 普朗特尔流体力学基础[M]. 北京: 科学出版社, 2008.
|
| [10] |
钱学森, 于景元, 戴汝为. 一个科学新领域——开放的复杂巨系统及其方法论[J]. 自然杂志, 1990, 13(1): 3-10. |
| [11] |
洪华生, 邓汉忠. 工程中的概率概念[M]. 陈建兵, 彭勇波, 刘威, 等译. 北京: 中国建筑工业出版社, 2017.
|
| [12] |
王振东, 武际可. 力学诗趣[M]. 天津: 南开大学出版社, 1998.
|
| [13] |
赵凯华. 定性与半定量物理学[M]. 北京: 高等教育出版社, 2008.
|
| [14] |
王大钧, 王其申, 何北昌. 结构力学中的定性理论: 解的定性性质与存在性[M]. 北京: 北京大学出版社, 2014.
|
| [15] |
丁洁民, 巢斯, 赵昕, 等. 上海中心大厦结构分析中若干关键问题[J]. 建筑结构学报, 2010, 31(6): 122-131. |
 2022, Vol. 31
2022, Vol. 31

