b. 重庆大学 山地城镇建设与新技术教育部重点试验室, 重庆 400044;
c. 重庆大学 建筑城规学院, 重庆 400044
b. Key Laboratory of New Technology for Construction of Cities in Mountain Area, Chongqing University, Chongqing 400044, P. R. China;
c. School of Architecture and Urban Planning, Chongqing University, Chongqing 400044, P. R. China
全国大学生结构设计竞赛是由教育部、财政部首次联合批准发文的全国性9大学科竞赛资助项目之一,也是土木工程专业的最高水平赛事之一,自浙江大学2005年承办第一届始,已举办13届。大赛旨在进一步培养大学生创新意识、团队协同和工程实践能力[1-2],切实提高创新人才培养质量。从第5届开始,竞赛选用的材料均为以楠竹为原材料加工制作的竹皮,然而,随着大赛的开展,模型制作和构件设计方面的不足日渐显现。由于缺乏竹皮构件设计的理论指导,学生在进行模型制作时,需要进行大量的摸索和破坏实验以寻求最优方案。这种低效寻求最优解的现状亟待改进,国内相关研究者也对此做了一定的研究。
常林海等[3]进行了竹皮的材料力学性能试验,得到了弹性模量、极限抗拉强度,并拟合得到了受拉构件极限承载能力与构件宽度的关系。雷鸣宇等[4]对18个圆筒试件进行了轴压试验,试验结果表明,0.5 mm厚度竹皮材料相比0.35 mm厚度,其抗压强度更高,且竹筒高度越低,抗压强度越高;并建议制作抗压柱时,在适当位置添加加劲肋,以提高试件整体与局部稳定性。付善春等[5]对15个箱形截面受压杆件进行了试验,发现试件的抗拉承载力与试件的截面面积之间没有明显的正比关系。贾新聪[6]测试了湿度、层数和宽度等参数对材料抗拉性能的影响,并对0.35 mm和0.5 mm两种厚度竹皮制作的48个箱形截面压杆进行了试验研究,结果表明:竹皮压杆在一定高度范围内发生强度破坏,其抗压强度不随杆件高度改变而发生改变;但超过该范围后,同种规格试件的抗压强度随着试件高度的增加而降低,此时竹条受压破坏主要是由于杆件失稳引起的。上述研究为结构设计分析和计算机模拟提供较为精确的材料性能数据,但仍未提出科学系统的设计方法。
除了在材料和构件性能方面的研究外,有关结构选型[7]、设计制作分析[8-9]、组队方式[10]和教学启示[11]等方面的研究也日趋丰富。
竹皮构件的既有研究局限于定性分析了竹皮受压柱极限抗压强度与宽度及长细比的关系,尚无对构件的稳定性研究,不能较好指导构件的设计。为改善以模型破坏试验寻求最优解的现状,并为参赛者进行箱形截面构件截面设计时提供科学的理论指导,开展竹皮箱形截面柱整体稳定性能的试验,计算了临界长细比值,并提出竹皮箱形截面柱的柱子曲线与整体稳定性能的设计方法。
一、试验概况 (一)试件设计试验所用竹皮由杭州邦博(BAMBOO)科技有限公司提供,与结构设计大赛所用材料为同一供应商。试验前,对竹皮实际厚度进行了测量,其中0.35 mm规格竹皮实际平均厚度为0.4 mm,0.5 mm规格竹皮实际平均厚度为0.5 mm。
设计了0.35 mm与0.50 mm两种厚度竹皮等边箱形截面受压柱试件共114个,如图 1所示。每种规格箱形截面柱试件设置3种宽厚比:0.35 mm竹皮箱形截面柱宽厚比b/t为12.5、20和30;0.5 mm竹皮箱形截面柱宽厚比b/t为10、16和24。相同宽厚比试件的长细比λ设置为10~100,增长梯度为5。

|
图 1 等边箱形截面柱实物图 |
因长细比相同构件的稳定承载力受构件加工质量和制作工艺影响较大,而构件加工质量的好坏主要表现在构件初弯曲的大小。参考钢结构设计规范,构件初弯曲不超过1/1000。经测量统计,研究制作的构件初弯曲均不超过该值。
(二)材料性能试验和短柱试验0.35 mm和0.5 mm两种规格竹皮各取10个长160 mm、宽8 mm的材性试件,通过静力拉伸试验获取材料的基本力学性能(包括弹性模量E、抗拉强度fu、极限应变εu),试验结果的平均值见表 1。每种宽厚比(b/t)构件各取5个高宽比(h/b)均为2的短柱试件,试件尺寸及长细比λ见表 2,并通过轴压试验获取其局部失稳极限应力σu值,试验结果的平均值见表 2。
| 表 1 材性试验结果 |
| 表 2 短柱试验结果 |
试验采用FBS-5000N微机控制电子万能试验机进行竖向加载。试件两端为刚度远大于试件的加载圆盘,由于试件端截面较小,圆盘对试件转动约束较小,因此可近似视为两端铰接。
测量设备包括试验机配套的力传感器、位移测量系统、变形测量系统、位移计等。位移计为量程25.4 mm的数显百分表,布置于试件跨中以测量试件失稳平面内的水平位移,试验装置自带位移测量系统可直接测量试件的竖向变形,即柱顶端加载点位移。
试验以1 mm/min的速度进行位移加载,试验机自行采集荷载峰值和位移值,并绘制荷载-位移曲线。当试验力值下降超过峰值的50%时停止加载。
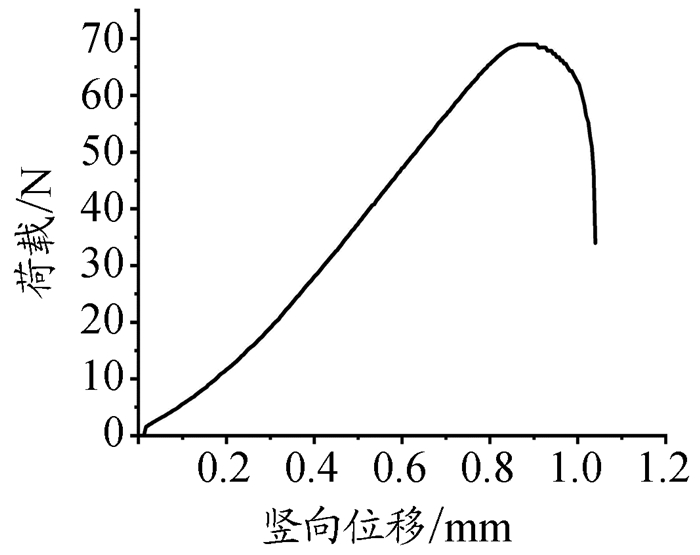
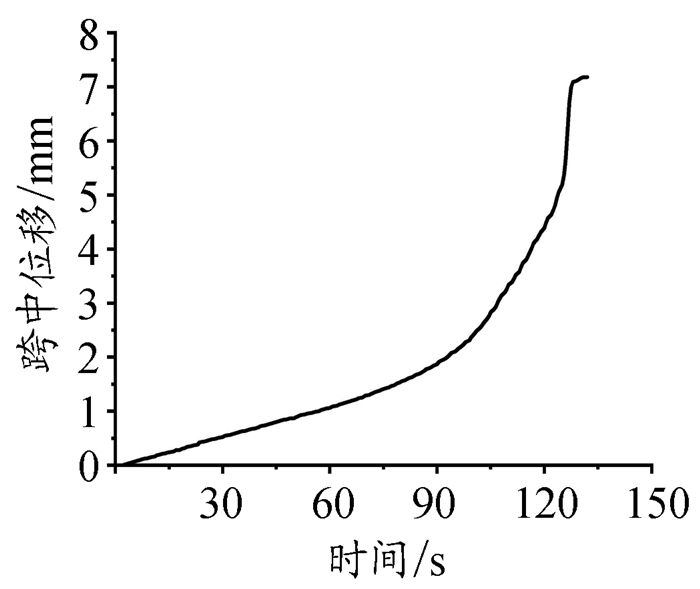
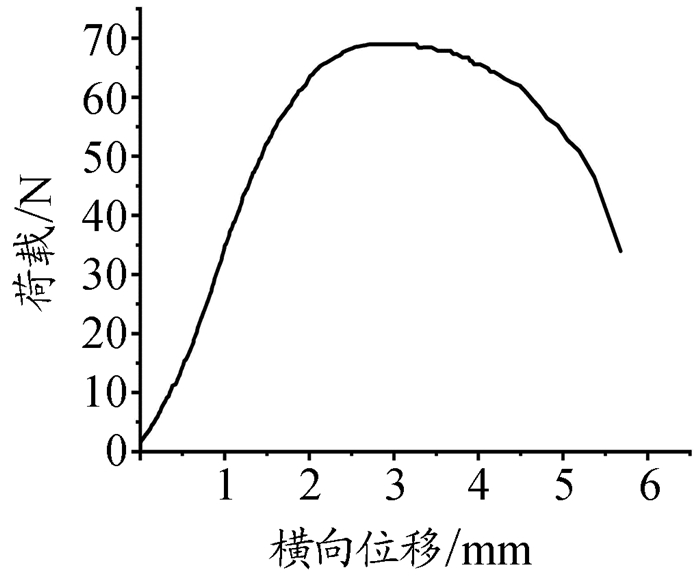
二、试验结果及分析 (一)试件破坏形式及变形分析试件典型的失稳破坏形态如图 2所示。构件在受荷时同时存在局部稳定和整体稳定问题,但长细比小于临界长细比的试件,以局部失稳破坏为主,如图 2(a)所示。发生局部失稳时,试件局部呈波浪状,各截面均达到局部屈曲临界荷载。在加载初期荷载位移呈线性变化,随着荷载逐渐增大,组成构件的板件开始发生局部屈曲,板件从上至下呈波浪形,初始波幅较小,此时已有部分板件退出工作,但构件仍具有一定的屈曲后强度,随着荷载继续增大,板件波幅也继续增大,最终由于波幅过大引起试件破坏。长细比大于临界长细比的试件,以整体失稳破坏为主,如图 2(b)所示。试件一经加载即产生挠曲,而挠度v不是随着压力N按比例增加,开始时,挠度增加慢,随后增加较快,如图 4、图 5所示。当挠度增加到一定程度时,杆件中点截面在轴力N与弯矩N·v作用下,受压侧板件应力达到局部屈曲临界应力,此时,板件开始发生凹凸,即产生局部屈曲,当达到局部屈曲极限应力时,试件破坏,竖向承载力开始下降。图 3、图 4和图 5分别为试件典型整体失稳试件的荷载—竖向位移曲线、跨中位移—时间曲线和荷载—横向位移曲线。

|
图 2 竹皮轴压箱形截面柱典型失稳破坏形态 |
|
图 3 荷载—竖向位移曲线 |
|
图 4 跨中位移—时间曲线 |
|
图 5 荷载—横向位移曲线 |
轴心受压构件的整体稳定系数φ表征构件失稳时极限承载力与短柱极限承载力的比值,即
| $ \varphi = {N_u}/A{\sigma _u} $ | (1) |
式中,Nu为极限承载力,A为试件横截面面积,σu为对应宽厚比箱形截面短柱极限强度试验值。
欧拉曲线表达式为
| $ \varphi = {N_E}/A{\sigma _u} $ | (2) |
| $ {N_E} = \frac{{{\pi ^2}EA}}{\lambda } $ | (3) |
式中, E为材料的弹性模量,采用表 1中的实测值。
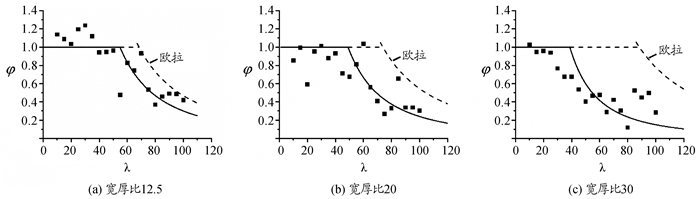
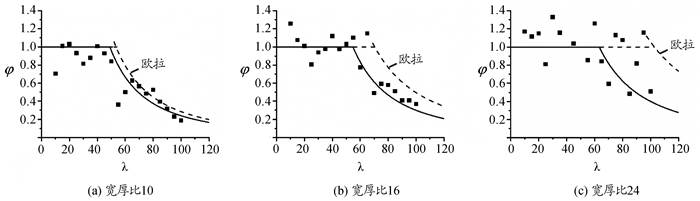
由试验结果计算得到轴心受压柱的整体稳定系数φ,计算结果绘于图 6和图 7中,并对试验数据进行拟合。图中部分试验结果值高于欧拉计算值,主要原因为材料的弹性模量为平均值,部分材料的弹性模量偏大,或者材料实际厚度偏大。两种规格箱形截面柱稳定系数拟合曲线均低于对应的欧拉曲线,且对于0.35 mm竹皮箱形截面柱拟合曲线偏离欧拉曲线较多,说明构件均存在初始缺陷,但0.5 mm竹皮箱形截面柱受初始缺陷的影响较0.35 mm竹皮箱形截面柱更小。
|
图 6 0.35 mm规格竹皮不同宽厚比构件稳定系数及拟合曲线 |
|
图 7 0.5 mm规格竹皮不同宽厚比构件稳定系数拟合曲线 |
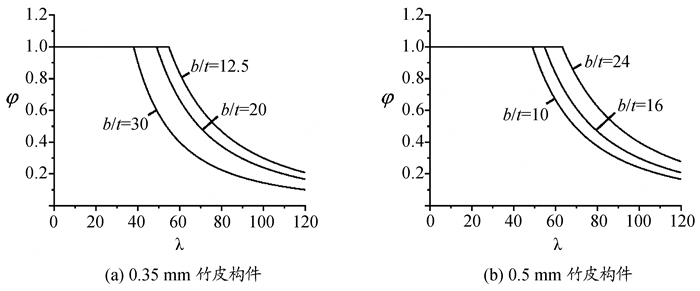
图 8为两种规格竹皮构件不同宽厚比下的柱子曲线。对于0.35 mm规格竹皮箱形截面构件,宽厚比越小,构件局部失稳破坏与整体失稳破坏的临界长细比值越大,且对于同一长细比,构件宽厚比越小,整体稳定系数值越大;对于0.5 mm规格竹皮箱形截面构件,宽厚比越小,构件局部失稳破坏与整体失稳破坏的临界长细比值越小,且对于同一长细比,构件宽厚比越小,整体稳定系数值越小。
|
图 8 柱子曲线 |
对于理想轴心受压构件,若仅考虑弯曲变形而忽略剪切变形的影响,其失稳临界力为欧拉临界力。但实际构件通常具有一定的几何初始缺陷(包括几何初弯曲、材料不均匀和端部荷载偏心),构件受压时发生极值点失稳,其临界力通常小于欧拉临界力。引入系数β对欧拉临界力进行修正,实际轴心受压构件稳定承载力按式(4)计算。
| $ N = \beta \frac{{{\pi ^2}EA}}{{{\lambda ^2}}} $ | (4) |
式中,系数β综合考虑各种初始缺陷的影响。
为简化,设计常采用的稳定承载力计算式为
| $ N = \varphi \cdot {\sigma _u}A $ | (5) |
根据式(5),压杆的稳定系数可表示为
| $ \varphi = \beta \frac{{{\pi ^2}E}}{{{\lambda ^2}{\sigma _u}}} $ | (6) |
带入实测数据,并通过拟合与反算确定了初始缺陷影响系数β值,见表 3。
| 表 3 初始缺陷系数与临界长细比 |
杆件的局部失稳破坏与整体失稳破坏的临界长细比λc可以按照实际轴心受压构件稳定承载力公式进行计算,并从以下条件得出结果
| $ \beta \frac{{{\pi ^2}E}}{{\lambda _c^2}} \le {\sigma _u} $ | (7) |
由式(7)知
| $ {\lambda _c} \ge {\rm{ }}\sqrt {\beta \frac{{{\pi ^2}E}}{{{\sigma _u}}}} $ | (8) |
λc值计算结果见表 3。
当λ≤λc时,构件极限承载力按强度进行计算
| $ {N_u} = {\sigma _u} \cdot A $ | (9) |
当λ>λc时,构件极限承载力按稳定进行计算
| $ N = \varphi \cdot {N_u} = \varphi \cdot {\sigma _u} \cdot A $ | (10) |
| $ \varphi = \beta \frac{{{\pi ^2}E}}{{{\lambda ^2}{\sigma _u}}} $ | (11) |
其中, β取值见表 3,弹性模量E与极限强度σu取实测值,见表 1、表 2。
(二)箱形截面构件设计建议竹皮构件稳定承载力受材料本身初始缺陷与构件制作加工水平的影响较大,在进行截面设计时,不能仅套用计算公式,还需对材料缺陷率与制作加工水平进行总体评定。在进行了箱形截面试件的试验与理论研究的基础上总结出箱形截面构件设计的建议。
(1) 构件的稳定承载力主要受竹节、微裂缝、初弯曲等初始缺陷的影响。对于材料本身的缺陷,可通过滴加胶水或贴竹皮的方式进行补强或在设计时对其实测强度进行折减,强度的折减系数可根据补强方式制作相应的试件通过试验确定。
(2) 本试验制作的构件无明显弯曲、扭转等缺陷,质量较好,试件均未发生因制作加工原因导致的局部破坏,计算公式并不适用于存在制作加工缺陷的构件。对制作加工质量缺陷的考虑,可基于制作加工者的手工制作水平和其加工的构件的缺陷率,按照一定的承载力保证率对稳定系数进行折减。
(3) 对6种宽厚比试件进行了试验与理论分析,从结果可以看出,对于同一长细比,0.35 mm规格竹皮构件稳定系数与宽厚比大致呈负相关,0.5 mm规格竹皮构件稳定系数与宽厚比大致呈正相关。因此,当制作的构件刚好为本文所研究的相同宽厚比构件时,可直接利用公式进行计算;当制作的构件为其他宽厚比时,可通过适当调整稳定系数进行设计,以保证设计值相对准确。
四、结论(1) 箱形截面构件在受荷时同时存在局部失稳与整体弯曲失稳问题。长细比小于临界长细比的构件在受压时以局部失稳为主,长细比大于临界长细比的构件以整体失稳为主。
(2) 得到0.35 mm与0.5 mm两种规格竹皮箱形截面构件柱子曲线。对于0.35 mm规格竹皮箱形截面构件,宽厚比越小,构件局部失稳破坏与整体失稳破坏的临界长细比值越大,且对于同一长细比,构件宽厚比越小,整体稳定系数值越大;对于0.5 mm规格竹皮箱形截面构件,宽厚比越小,构件局部失稳破坏与整体失稳破坏的临界长细比值越小,且对于同一长细比,构件宽厚比越小,整体稳定系数值越小。
(3) 计算了两种规格竹皮各3种宽厚比箱形截面构件的临界长细比值。对0.35 mm厚竹皮,宽厚比为12.5、20和30的试件,其临界长细比分别为54.8、49.0和38.7;对0.5 mm厚竹皮,宽厚比为10、16和24的试件,其临界长细比分别为49.0、54.8和63.2。
(4) 通过理论分析与数据拟合,得出两种规格竹皮各3种宽厚比箱形截面构件的极限承载力计算公式,并提出了箱形截面构件的设计建议。
| [1] |
陈俊岭, 黄皇. 结构模型竞赛在土木工程专业大学生创新能力培养中的作用[J]. 高等建筑教育, 2014, 23(2): 103-107. |
| [2] |
熊沩, 陈云, 姜宝石. 大学生结构设计竞赛对学生能力培养的探讨[J]. 高等建筑教育, 2015, 24(6): 137-140. |
| [3] |
常海林, 张旭钦, 钱格军, 等. 大学生结构设计大赛材料力学性能试验研究[J]. 高等建筑教育, 2017, 26(5): 108-114. |
| [4] |
雷鸣宇, 蒲万丽, 廖益林, 等. 竹皮材料综合力学性能探究[J]. 工业技术创新, 2016, 03(5): 949-952. |
| [5] |
付善春, 尹祖兴, 杨倩文, 等. 竹材构件材料力学性能及承载力研究[J]. 河南工程学院学报(自然科学版), 2017, 29(4): 49-52, 82. |
| [6] |
贾新聪. 结构竞赛模型材料物理力学性能及模型设计制作研究[D]. 华北水利水电大学, 2018.
|
| [7] |
马宏亮, 韩伊彤, 于景东, 等. 建筑结构模型设计中的选型与设计——以2014年辽宁省大学生结构设计大赛赛题为例[J]. 科技创新与应用, 2015(8): 172. |
| [8] |
刁泽民, 陈富廉, 李宏涛, 等. 结构设计大赛中的计算机仿真分析[J]. 电脑知识与技术, 2017, 13(8): 207-208, 248. |
| [9] |
邹翼, 王庆, 程玉珍, 等. 竹皮结构设计与制作分析[J]. 高等建筑教育, 2018, 27(4): 73-81. |
| [10] |
侯鹏程, 李悦, 杜修力. 关于我院结构设计大赛组织工作的几点思考[C]//高等学校土木工程专业建设的研究与实践——第十届全国高校土木工程学院(系)院长(主任)工作研讨会论文集. 长沙, 2010: 331-333.
|
| [11] |
乔朋, 李悦, 马乾瑛. 大学生结构设计竞赛对结构力学课程教学的启示[J]. 高等建筑教育, 2019, 28(5): 74-79. |
 2022, Vol. 31
2022, Vol. 31

