随着信息技术的高速发展,在当代大学生面前,传统的灌输式教学魅力和效果大为下降[1]。近年来,在“以学生为中心”的教育理念下,大学的目的不在“教”,而在于让每位学生有效地“学”,大学从提供教学转向为学生创造自主学习环境[2],教学重心落在培养学生自主思考和自主学习的能力上。
本文以结构力学为例,探讨“以学生为中心”的教学模式。在结构力学的传统教学模式中,教师上课时更注重原理和概念的讲解,学生解题时更注重解题步骤和方法,学生面对复杂问题时无法抓住重点,无解题思路。结构力学课程的教学难点在于结构形式多样化,不同的结构力学问题有不同的特点,虽然对于大多数问题有矩阵位移法、有限元法等通用解法,只要掌握方法后即可计算,但计算量较大,通常需要借助计算软件。计算软件的发展使结构力学中繁琐的计算变得容易实现,却并未使学生的能力素养得到全面提升。反而,过度依赖软件,部分学生愈加缺乏独立思考能力,甚至对基本的力学概念和理论理解也变得模糊[3]。因此,结构力学这门课的教学应注重培养学生对概念的理解掌握,根据结构本身的特点来寻找简便的计算方法。
为解决上述结构力学教与学的矛盾,提高教学质量,提出了面向学生自主学习能力的概念分析教学方法,以此提高学生的自主学习能力。力学概念是结构力学的基础和核心,学生只有掌握了力学概念,才能真正学懂结构力学[4]。概念分析对学生的综合能力有较高的要求,教学难度较大。为实现概念分析教学,本文采用递进式方法,将概念分析能力培养分为三个阶段——概念理解能力、概念辨析能力和概念灵活应用能力,分别设置三个层次的题型——易错题、易混淆题和多解题。易错题:设置与基本概念有关的习题,培养学生的概念理解能力。易混淆题:设置相似却并不相同的习题,培养学生的概念辨析能力。多解题:设置存在多种解法的复杂习题,培养学生的概念灵活应用能力。
各以一个习题为例分别讲解易错题、易混淆题和多解题设置的方法和要点,并阐述其与概念分析能力培养的关系。通过递进式概念分析教学的具体方法,提供可参考的递进式概念题组。
一、概念理解——易错题设置在结构力学的学习中,学生若对基本概念的理解不到位,则无法做到解题过程与前提条件的逻辑一致,会出现许多易错点,可根据这些易错点来设置易错题。以弯矩分配法为例,弯矩分配法是一种数值计算方法,因此正负号约定十分重要。在弯矩分配法的解题过程中,由于涉及的弯矩类型和需要判断弯矩正负号的次数较多,各类弯矩的符号判断是一个易错点。因此,可以将求解弯矩分配法中用于分配的弯矩(以下简称待分配弯矩)概念设置为易错题,让学生思考并解释待分配弯矩究竟是什么弯矩,又是如何得到的,加深学生对待分配弯矩概念的理解。不同学生对这个问题的理解角度不同,他们的理解方式和求解方法也不同。
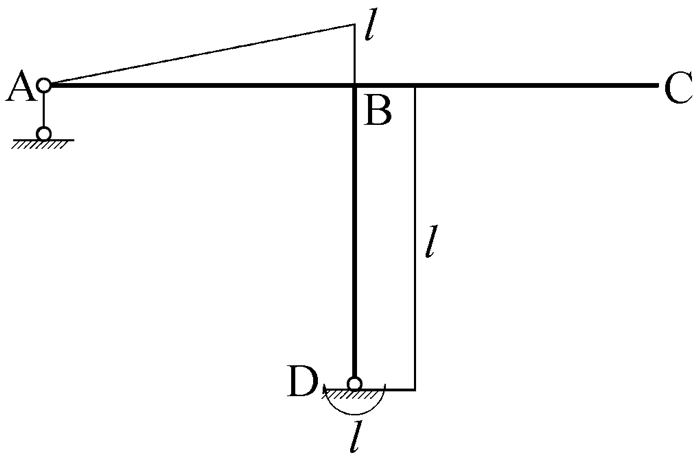
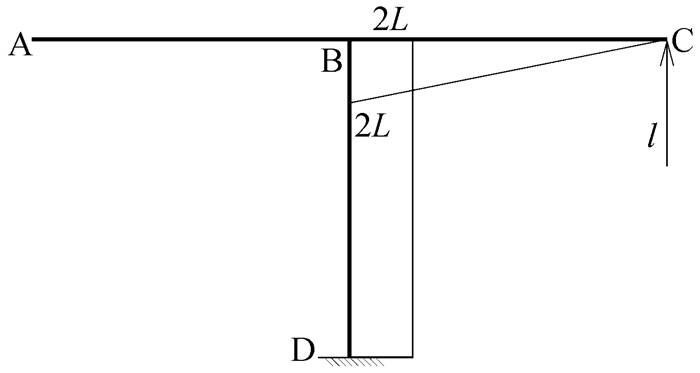
以一个简单的单结点刚架为例,AB段作用均布荷载,A结点处作用集中力矩,如图 1所示,求此刚架的待分配弯矩。
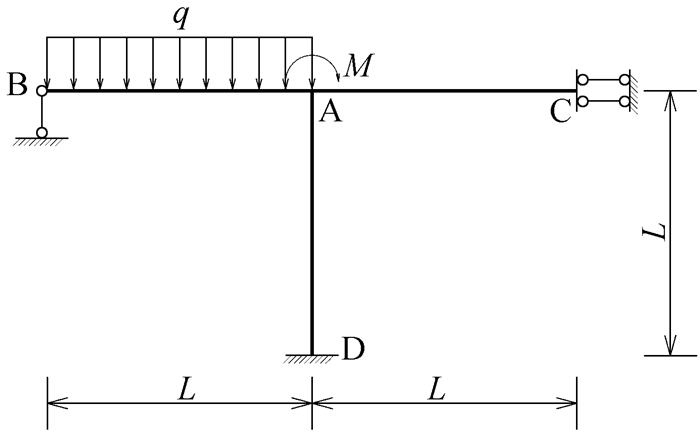
|
图 1 均布荷载和结点集中力矩作用下的单结点刚架 |
求解上述习题中的待分配弯矩,有以下几种常用的理解方式和求解方法。
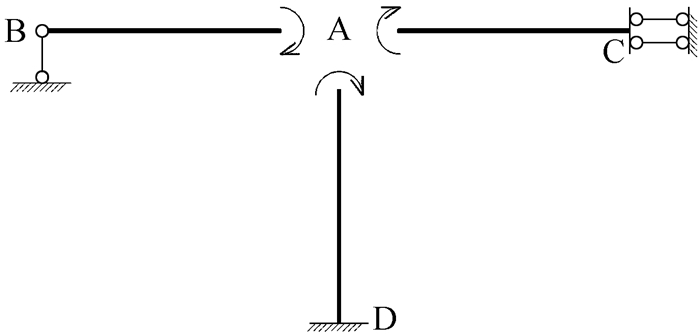
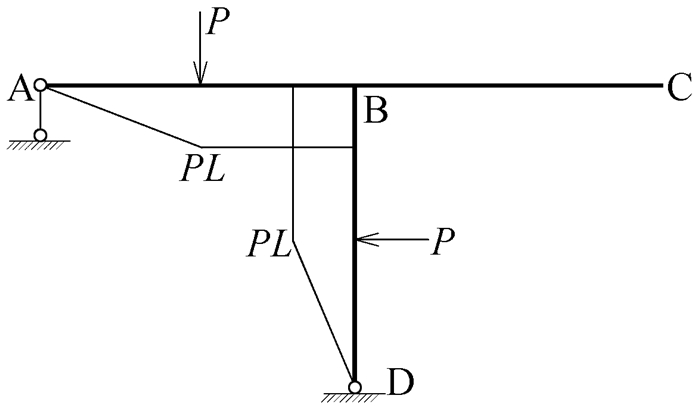
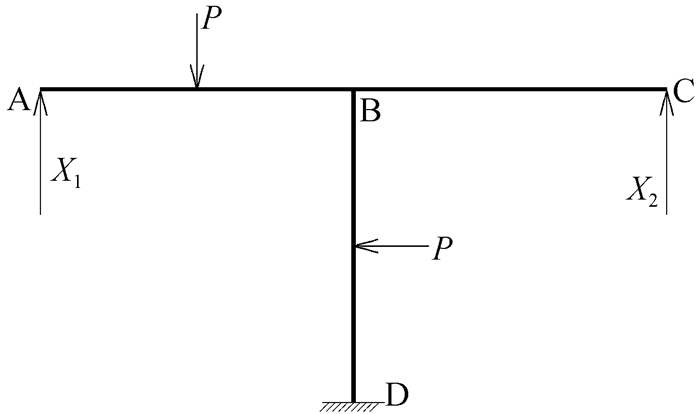
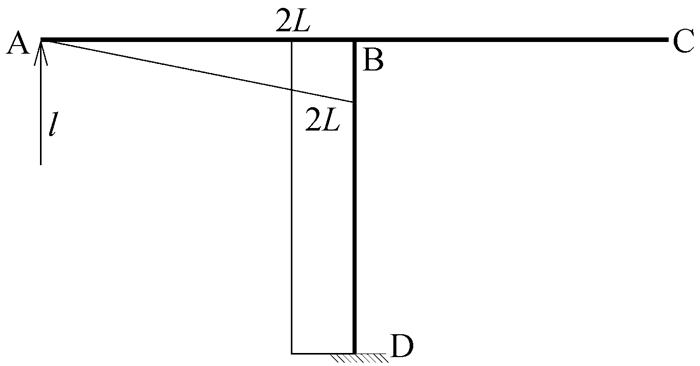
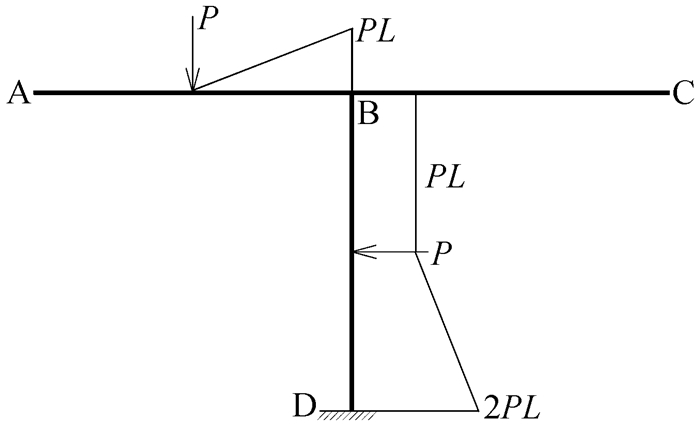
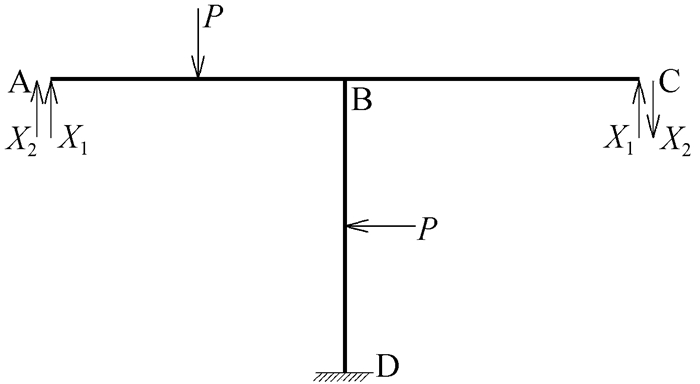
第一种理解方式从待分配弯矩概念的角度出发,待分配弯矩是向杆端进行分配的。首先,将该刚架分解为只受集中力矩作用和只受均布荷载作用两种情况,分别如图 2和图 3所示。先考虑只受结点集中力矩作用的情况,在顺时针集中力矩的作用下,可根据平衡条件画出A结点隔离体弯矩示意图,如图 4所示。根据作用力与反作用力原理,可画出AB、AC、AD三根杆件在靠近A端的杆端弯矩示意图,如图 5所示。

|
图 2 集中力矩作用下的单结点刚架 |
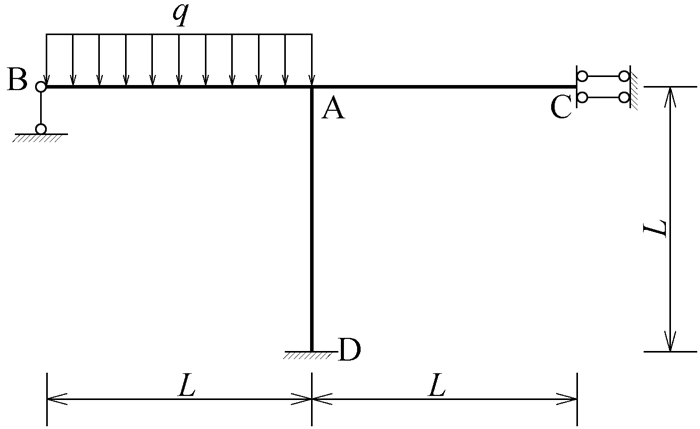
|
图 3 均布荷载作用下的单结点刚架 |
|
图 4 A结点隔离体弯矩 |
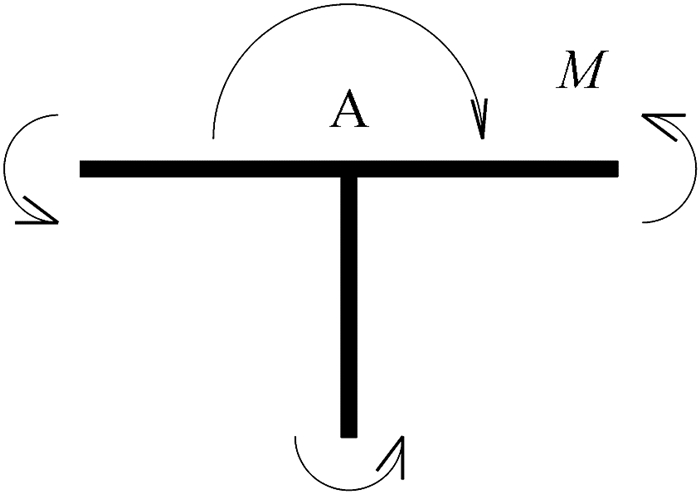
|
图 5 三杆A端隔离体弯矩 |
观察图 5可发现,三根杆件靠近A端的杆端弯矩均为顺时针,与A结点的集中外力矩方向相同。说明结点弯矩荷载和与该结点相连的杆端弯矩方向相同,弯矩分配法中的待分配弯矩就是作用在结点上的弯矩。考虑结构在一般荷载作用下的情况,在结点处附加刚臂约束,将一般荷载转化成结点弯矩荷载,再进行分配。附加刚臂约束后,刚结点处各杆端弯矩的代数和称为不平衡弯矩,并由此形成了附加刚臂中的约束力矩[5]。释放附加刚臂约束后,该约束力矩反向施加在结点上,转化成结点弯矩荷载,即待分配弯矩。许多学生将附加刚臂上的约束力矩当作待分配弯矩,这便是对待分配弯矩的概念理解有误。附加刚臂上的约束力矩是假想的、虚拟的,而待分配弯矩是真实存在、可用于分配的,这二者的概念不能混为一谈。根据上述分析,总结出一个简单的待分配弯矩公式:结点待分配弯矩=该结点弯矩荷载-该结点固端弯矩代数和。
第二种理解方式从固端弯矩符号规定角度出发,用上述公式求解时,需注意各类弯矩的正负号。其中,固端弯矩规定绕杆端顺时针为正,该弯矩的符号判断是学生容易出错的地方。以两端固定、跨中作用集中荷载的等值截面杆为例(图 6),取出中间杆单元隔离体(图 7)。对于杆单元隔离体来说,左侧杆端弯矩为上侧受拉,方向为绕左杆端逆时针,弯矩取负号;右侧杆端弯矩也为上侧受拉,方向为绕右杆端顺时针,弯矩取正号。综上,固端弯矩可根据弯矩图总结为“左下右上为正”。求固端弯矩时可通过载常数表记住弯矩图形形状,利用“左下右上为正”的口诀来判断正负号。
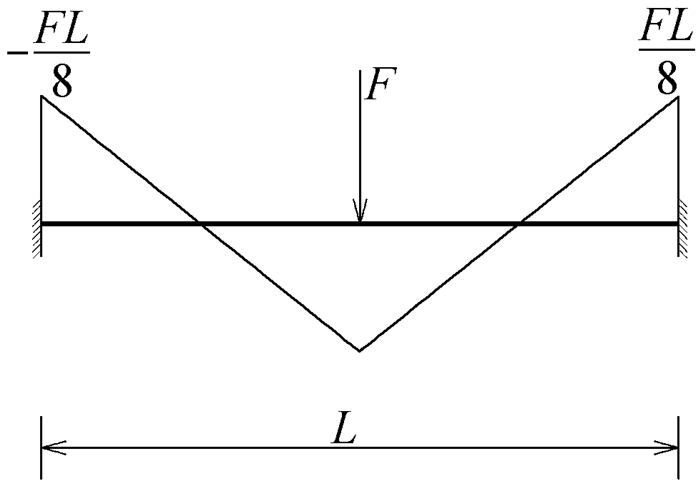
|
图 6 跨中作用集中荷载的等值截面杆 |
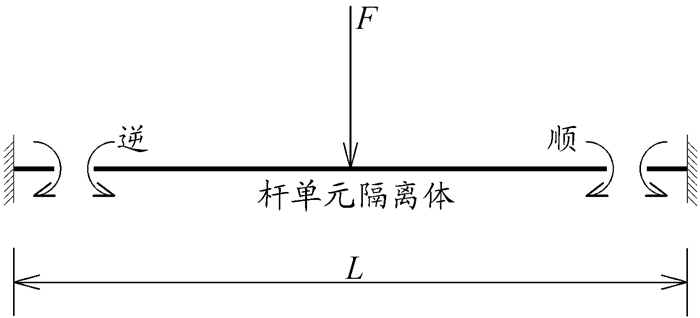
|
图 7 杆单元隔离体 |
第三种理解方式,学生不考虑各类弯矩的符号规定,只根据各类弯矩的方向求解。这种情况下,学生采用同向取正、逆向取负的计算方法求出待分配弯矩的值,降低了判断正负号时的出错概率。
第一种方法从待分配弯矩概念的角度给出了待分配弯矩的实质,即作用在结点处的弯矩,并总结了待分配弯矩的求解公式;第二种方法从固端弯矩符号规定的角度出发给出判断固端弯矩正负号的口诀;第三种方法省去了判断正负号这一步骤。三种方法各有千秋。
此类习题的设置目的是引导学生自主思考基本概念,提升学生的概念理解能力。学生从不同角度出发,总结不同的解题技巧。在课堂上,学生互相交流各自的理解方式,开拓思维,从不同角度理解同一概念,使学生对概念的理解更深刻。同时,不同学生接受的理解方式不同,从学生的角度提出多种理解方式,根据需要选择适合自己的方式。教师也可归纳总结适合大多数学生理解的解题方式。譬如此例中,推荐学生采用第一种方式来理解待分配弯矩的概念并求解。
二、概念辨析——易混淆题的多题对比设置在结构力学中,存在许多易混淆的概念。学生在解题时,容易混淆题目所给条件与其他相似条件,无法抓住重点,导致出错。究其根本原因,是学生缺乏概念辨析能力。分别归纳整理各类易混淆概念,呈现在习题中,让学生在解题过程中自主总结易混淆概念的不同之处和对最终结果的影响。
下面以力法求解超静定结构内力的习题为例进行讲解。
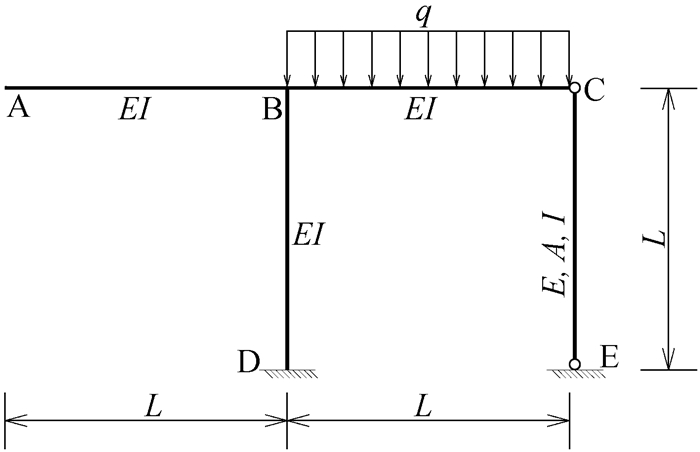
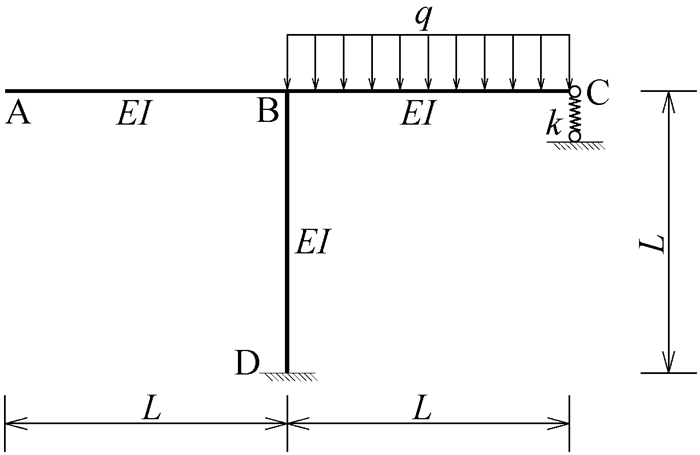
力法求解超静定结构的关键在于利用变形协调条件列出力法基本方程,若多余约束不同,则该多余约束处的实际位移不同,力法基本方程等号右端项就不同。如图 8—图 11所示,这四个超静定结构中除C处的约束条件不同——分别为可动铰支座、存在支座位移的可动铰支座、有轴向刚度的弹性杆和弹簧支座,其余各处的条件均相同,均存在一个多余约束的超静定结构。
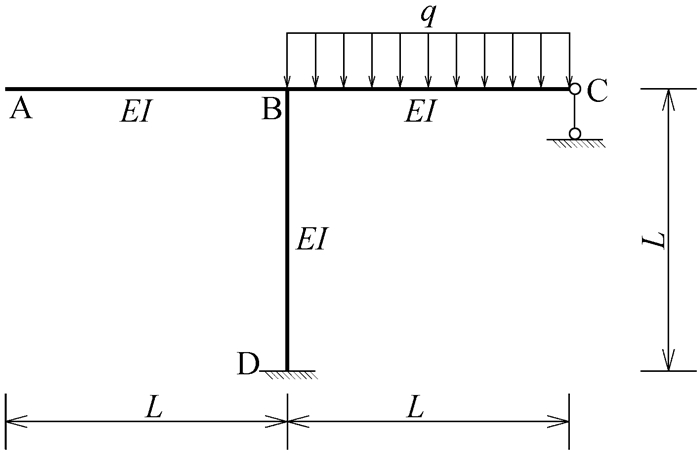
|
图 8 可动铰支座习题 |
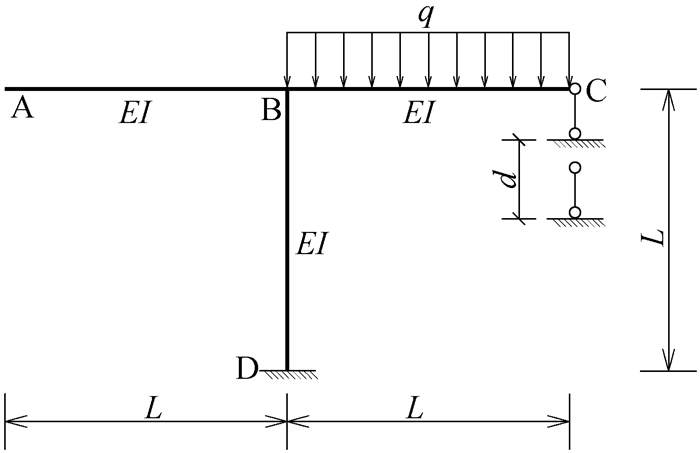
|
图 9 有支座位移的可动铰支座习题 |
|
图 10 有轴向刚度的弹性杆习题 |
|
图 11 弹簧支座习题 |
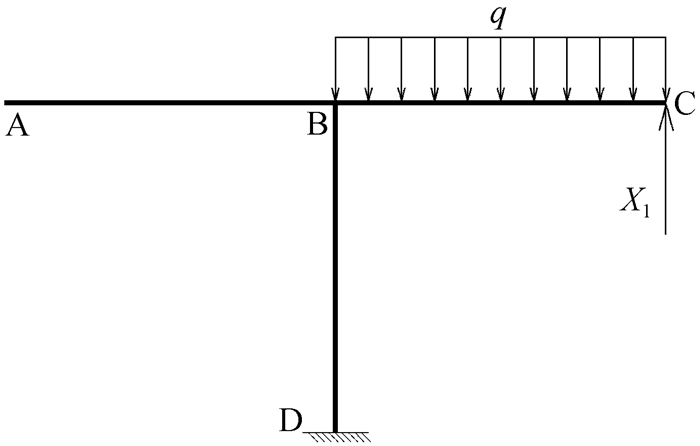
若采用力法来求解其内力,都选取C处的约束为多余约束,四题的基本体系相同,如图 12所示。
|
图 12 基本体系示意图 |
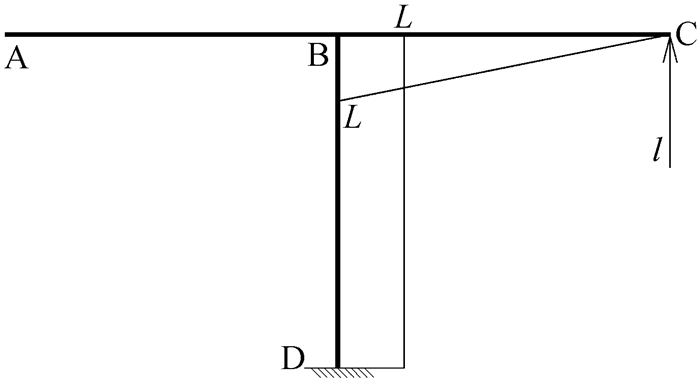
因为这四题的基本体系和外荷载都相同,所以M1图和Mp图也相同,分别如图 13和图 14所示。由图乘得出的柔度系数和自由项也相同,分别为
|
图 13 四道习题的M1图 |
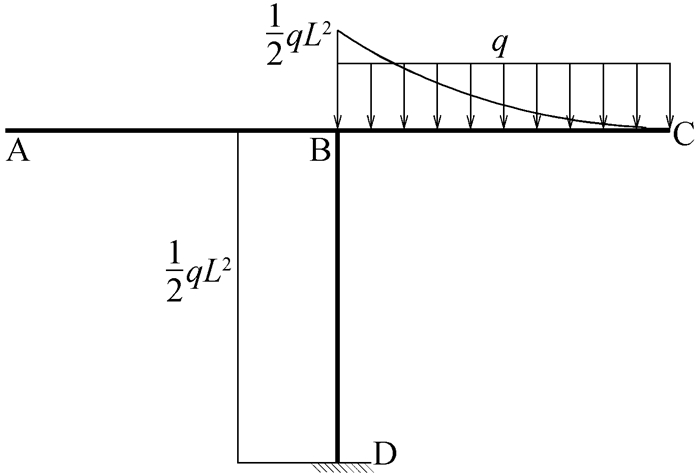
|
图 14 四道习题的Mp图 |
接下来,列出形如式(1)的力法基本方程[5]。由于基本未知量、柔度系数和自由项都相同,四道习题的力法基本方程等号左边的式子完全相同。而这四道习题的原结构在C处的约束条件不同,导致其在C处的真实位移Δc不同,所以力法基本方程的右端项不同。例1可动铰支座的竖向位移为0;例2支座在C处产生-d的支座位移;例3弹性杆产生
| δ11X1+Δ1p=Δc | (1) |
由力法基本方程解得基本未知量,继而求得四道习题中超静定结构的内力,此处不再赘述。
从上述解题过程可看出,将不同支座的概念放在一套习题中,通过对比来体现概念的差异,让学生在解题过程中分辨这些易混淆概念。通过多题对比,在解题过程中提高学生的概念辨析能力。
值得注意的是,概念辨析能力建立在学生的概念理解能力基础上。例如,本章所述习题,学生需要理解弹性杆的概念,根据题目所给的E、A、I条件,判断其为弹性杆,产生轴向位移,将其与其他支座区别,进行对比辨析。在多题对比的过程中,学生的概念理解能力也进一步得到锻炼。
三、概念灵活应用——多解题设置在结构力学中,复杂题目有多种解法,不同解法各有利弊,且时常存在最简解法。许多学生解题时不灵活,会采用最直接想到的解法,而不去思考是否有简便解法,常因复杂的解题步骤而出错。寻找题目的不同解法,需要学生从题目的特征出发,利用题目所给的一些特殊条件得到简便解法。多解题的设置,鼓励学生观察题目特征,采用多种方法来解题,并自主总结最简解法,锻炼学生对概念的灵活应用能力。
以求解一个在非对称荷载作用下的对称结构(图 15)内力习题为例进行说明。
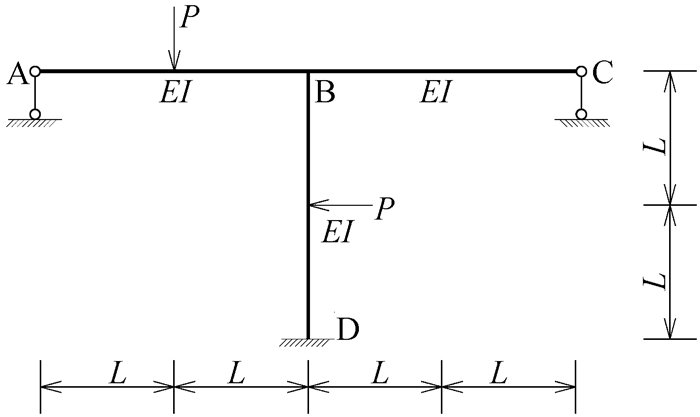
|
图 15 非对称荷载作用下的对称结构习题 |
首先,可以明确这是一个二次超静定结构,可以用力法求解,列出如式(2)和式(3)的力法基本方程
| δ11X1+δ12X2+Δ1p=0 | (2) |
| δ21X1+δ22X2+Δ2p=0 | (3) |
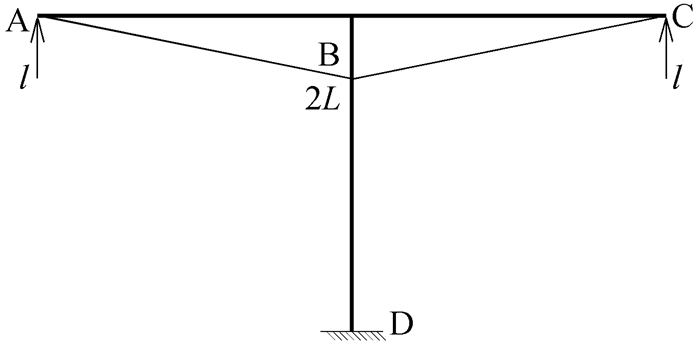
若学生没有观察到该结构对称性的特征,则会选取非对称的基本体系进行求解,即第一种解法。这里选取如图 16所示的一种非对称基本体系,画出M1图、M2图和Mp图,如图 17—图 19所示。求得柔度系数和自由项分别为
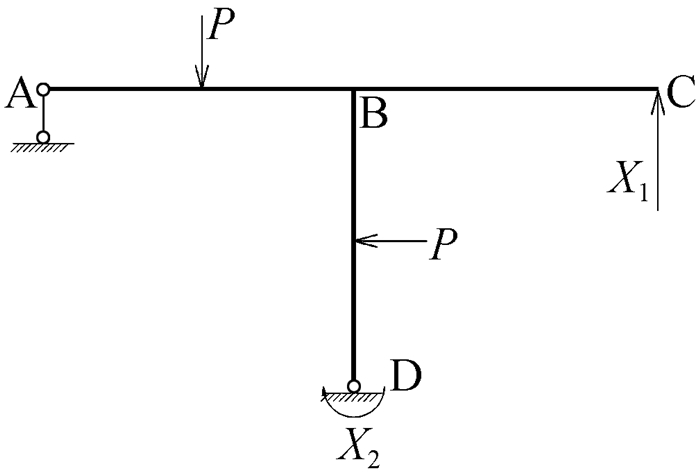
|
图 16 基本体系1示意图 |
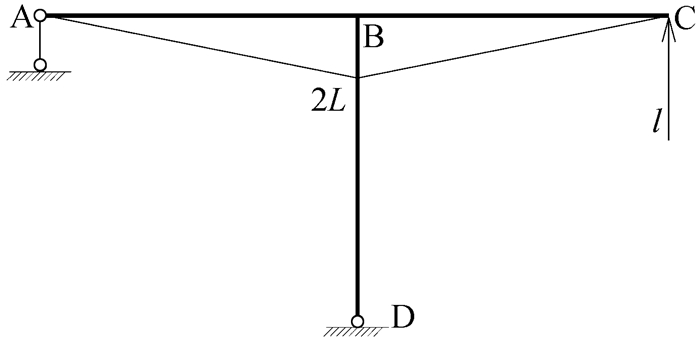
|
图 17 M1图示意图 |
|
图 18 M2图示意图 |
|
图 19 Mp图示意图 |
若学生观察到该结构对称性的特征,则会选取对称的基本体系,即第二种解法。选取A、C处的约束为多余约束,如图 20所示。由于作用荷载为非对称荷载,A、C处的约束反力不会相同,得到M1图、M2图和Mp图,如图 21—图 23所示。此方法中,基本体系对称,基本未知量X1和X2在相互对称的位置,所以M1图和M2图相互对称,柔度系数δ11和δ22相等,且δ12与Δ1p、Δ2p的计算也较第一种方法简便,说明对称性的初步应用减少了部分计算量与作图量,在一定程度上降低了出错率。计算得到柔度系数与自由项分别为
|
图 20 基本体系2示意图 |
|
图 21 M1图示意图 |
|
图 22 M2图示意图 |
|
图 23 Mp图示意图 |
若进一步利用对称性的概念,将第二种方法中的两个基本未知量替换为一组对称的基本未知量X1和一组反对称的基本未知量X2,即第三种解法,如图 24所示。在对称基本未知量X1作用下的M1图是对称的(图 25),在反对称的基本未知量X2作用下的M2图是反对称的(图 26),Mp图如图 27所示。采用此种方法,M1与M2图乘得到的交叉系数项δ12与δ21为零,δ11、δ22和Δ1p、Δ2p的计算也并不复杂。因此,式(2)和式(3)退化为两个一元一次方程,极大简化了求解X1和X2的过程,降低了出错率。求得的柔度系数和自由项分别为
|
图 24 基本体系3示意图 |
|
图 25 M1图示意图 |
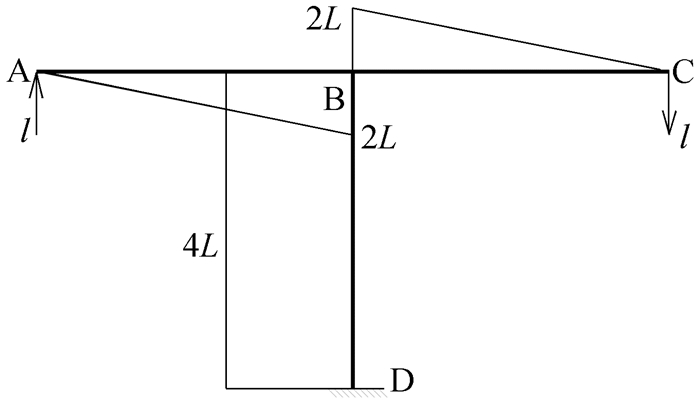
|
图 26 M2图示意图 |
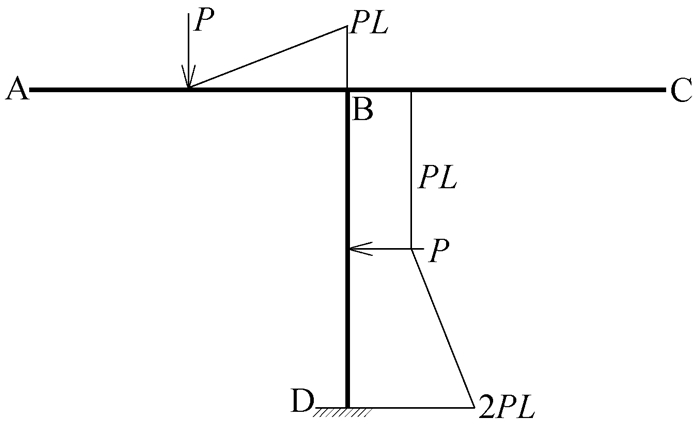
|
图 27 Mp图示意图 |
考虑到该结构为对称结构,还可采用半结构的解题方法,将二次超静定结构转化为一次超静定结构,即第四种解法。由于此题中荷载是非对称的,先将原荷载分解为一组对称荷载和一组反对称荷载,分别对其采用半结构解法计算内力后再进行叠加。对于此题来说,半结构解法较为复杂,不比第三种解法更简便,此处不再赘述。
对比以上四种解法发现,对称性的充分合理应用可以简化解题过程,第三种解法是最简解法。设置此类多解题的习题,鼓励学生从题目特征出发,采用多种解法解题,寻找最简解法,锻炼对概念的灵活应用能力。
同样的,概念灵活应用能力建立在概念理解能力与概念辨析能力基础上。例如,在上述习题中,学生需要理解对称性的概念,才能准确把握题目特征,提出第二、三、四种解法,并辨别各种解法的优缺点。在解多解题的过程中,学生的概念理解和概念辨析能力也会得到进一步提升。
四、递进式概念分析教学方法的实现学生自主学习能力的培养应与知识的难易程度安排相结合[6]。本文提出递进式概念分析教学方法来降低概念分析教学的难度,具体实现方法为:对于每章节的内容,教学结束后针对该章节知识点整理一套包含易错题、易混淆题和多解题的递进式概念题组,添加在各章节的作业中。递进式概念题组的内在关系如表 1所示。概念题组的递进关系从两方面来实现:1)概念分析上的递进关系,从基本概念到分支概念,再到概念的综合与简化,是一个由基础到提升的递进过程;2)题目难易程度上的递进关系,同一概念题组的结构形式相似,从基本题到复合题再到综合题,由简单到复杂,存在直观的递进关系。
| 表 1 递进式概念题组的内在关系 |
以弯矩分配法和力法两章的内容为例,可按表 2所述知识点分别整理出各章的递进式概念题组。
| 表 2 弯矩分配法和力法的相应习题 |
为更直观地体现递进关系,按表 2所述给出一套力法的递进式概念题组,供读者参考。易错题可按图 28设置,让学生选择合适的多余约束并探寻多余约束处变形协调条件与力法基本方程的关系。易混淆题可按图 29—图 32设置,即本文第2章内容中所述习题。此题由易错题衍生,将不同的约束条件整理在一起,供学生辨析。多解题可按图 33设置,该题结构形式与易错题和易混淆题相似,但超静定次数增加,题目难度加大。
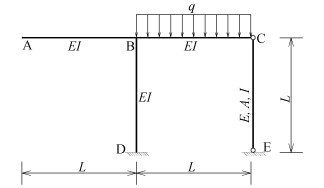
|
图 28 力法易错题习题 |
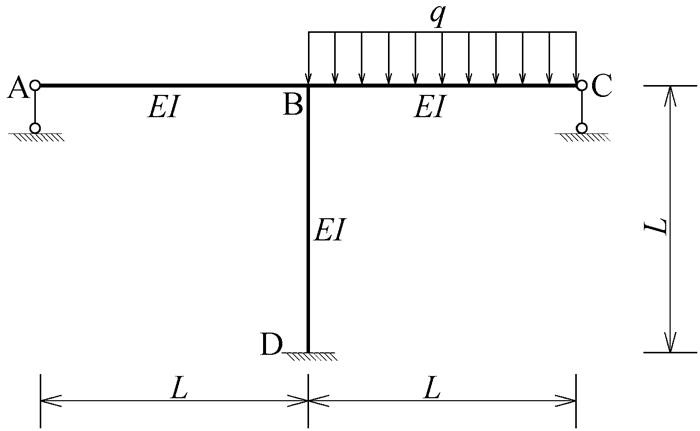
|
图 29 力法易混淆题习题1 |
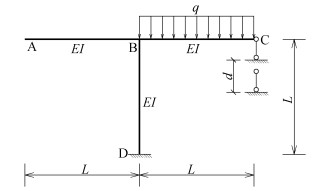
|
图 30 力法易混淆题习题2 |
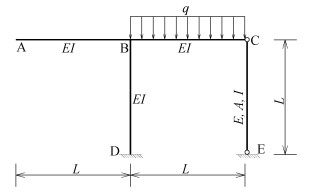
|
图 31 力法易混淆题习题3 |
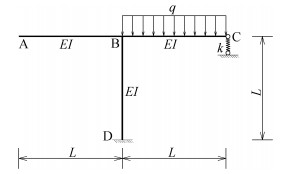
|
图 32 力法易混淆题习题4 |
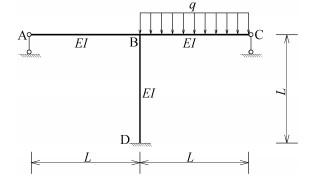
|
图 33 力法多解题习题 |
为实现“以学生为中心”的教学模式,以结构力学为例,从结构力学教与学的矛盾出发,给出面向学生自主学习能力的递进式概念分析教学方法。将概念分析能力培养分为概念理解、概念辨析和概念灵活应用三个阶段,分别设置易错题、易混淆题和多解题。在各章节设置递进式概念题组,引导学生从概念出发,在解题过程中总结易错题的简便解法、易混淆题的多题对比结论和多解题的最简解法,使学生准确理解和把握关键概念并融会贯通。
递进式概念题组从概念的基础到提升和题目的由易到难两方面来实现递进,可解决学生在概念分析方面的困难。通过易错题的设置,让学生关注基本概念,从不同角度理解同一概念,加强对概念的理解,从而提升概念理解能力;通过易混淆题的设置,将容易混淆的概念归纳整理成习题,让学生在多题对比的过程中对概念进行对比分析,从而提升概念辨析能力;通过多解题的设置,让学生从题目特征所涉及的概念出发,给出多种解法并总结最简解法,从而提升概念灵活应用能力。
| [1] |
邢以群, 鲁柏祥, 施杰, 等. 以学生为主体的体验式教学模式探索——从知识到智慧[J]. 高等工程教育研究, 2016(5): 122-128. |
| [2] |
周光礼, 黄容霞. 教学改革如何制度化——"以学生为中心"的教育改革与创新人才培养特区在中国的兴起[J]. 高等工程教育研究, 2013(5): 47-56. |
| [3] |
许凯, 陈朝峰, 杨祖权. 定性分析在结构力学教学中的应用研究[J]. 高等建筑教育, 2010, 19(6): 98-101. |
| [4] |
杜闯, 陈向上, 李静, 等. 重视结构力学课程力学概念的教学探讨[J]. 高等建筑教育, 2014, 23(6): 66-69. |
| [5] |
朱慈勉. 结构力学[M]. 北京: 高等教育出版社, 2004.
|
| [6] |
袁驷. 一个基础, 两座大厦——《结构力学》课程的改革思路与实践[J]. 力学与实践, 1998(4): 56-58. |
 2022, Vol. 31
2022, Vol. 31


