2. 武汉工程大学 土木工程与建筑学院,湖北 武汉 430074
2. School of Civil Engineering and Architecture, Wuhan Institute of Technology, Wuhan 430074, P.R. China
探究式教学是在教学过程中创设一种类似科学研究的情境,以课堂作为教师和学生沟通的主渠道,让学生在学习过程中独立自主地探究学科知识,从而理解、质疑、反思、批判、发展并创造学科知识,并从中发展与培养个性、思想、人格及社会责任感,全方位提高自身素质[1]。可见,探究式教学与传统教学模式存在显著差异。探究式教学更加注重学术深度,探讨基本教学内容的深层次内涵。教学实践中,适度追求教学内容的深度,可帮助学生加深对于基本教学内容的理解,并激发学生的专研精神和创新精神[2]。弹性力学是固体力学的重要分支,也是塑性力学等后继力学课程的重要基础,其理论被广泛应用于土木、水利、机械、航天等工程领域。然而,弹性力学相对于材料力学而言,其涉及的数学公式较多且复杂(多为偏微分方程),逻辑推理更为严密,计算工作量大,具有较强的理论性和抽象性,学生学习难度较大[3]。因此,在弹性力学教学过程中,应突出弹性力学的基本理论,向学生展现其丰富的内涵。同时,开展探究式教学,需注重从力学的基本原理方面挖掘基本教学内容的深度,引导学生从更深的层次上分析和理解这些内容。此外,教学中注重从工程案例中引入力学概念,并强调其物理意义和数学逻辑关系,强化研究方法和解题思路。使学生在理解基本教学内容的同时,能创造性地应用这些概念、原理以及公式去分析解决复杂的工程实际问题。
圣维南原理(Saint Venant’s Principle)在弹性力学中具有重要的理论与实际意义。弹性力学求解问题实质是偏微分方程组的边值问题。其中,偏微分方程组是弹性力学的共性问题;边界条件是弹性力学的个性问题。应力、位移等未知函数必须满足所有偏微分方程组和全部边界条件。其求解的困难主要在于难以满足边界条件。一方面,虽然大部分边界条件能精确满足,但在部分局部边界上的边界条件却较难精确满足;另一方面,工程中往往只知道作用于某一局部边界上的主矢量和主矩,而不清楚其面力的具体分布形式,因而无法精确地表达局部边界上的边界条件。而圣维南原理为简化局部边界上的应力边界条件提供了便利[4]。本文基于探究式教学的内涵与理念,在弹性力学课程教学过程中,以圣维南原理及其应用这一基本教学内容为例,通过对基本教学内容的深入阐述与延拓,开展了探究式案例教学的设计与实践。
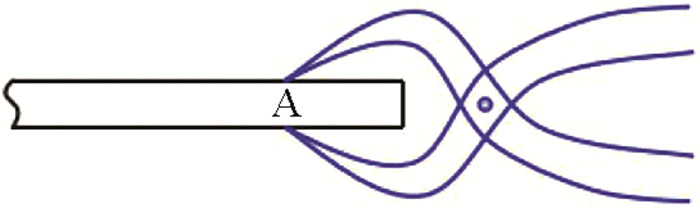
一、基本教学内容在工科专业的弹性力学课程教学中,圣维南原理及其应用的基本教学内容主要包括基本概念、基本问题和基本方法。通常,以钳子夹铁丝这一常见的生活实例为引子,如图 1所示,铁丝在A处被钳子夹紧,相当于在该处施加了一对平衡力系,无论作用力的大小,在所夹部位A处以外的其他部位几乎没有应力产生,甚至铁丝被钳子夹断后,A处以外的其他部位几乎不受影响。这个例子生动地说明了圣维南原理的真实性。
|
图 1 钳子夹铁丝 |
圣维南原理源于法国著名科学家圣维南。圣维南在1855年发现了一个现象:若将作用于物体局部边界上的面力,用另一组与它静力等效的力系来代替,则在力系作用区域近处的应力将有显著的改变,但在远处几乎不受影响。这就是局部效应原理,也称为圣维南原理。实际上,对于圣维南原理,关键在于如何理解局部边界(小边界或次要边界)、静力等效、近处以及远处等概念。
正如钳子夹铁丝的例子,在钳子夹铁丝的A处,相当于在该处施加了一对平衡力系。由此可引出圣维南原理的另一种表述:如果物体一小部分边界上的面力是一个平衡力系,那么,这个面力仅仅使近处产生显著的应力,而远处的应力可以忽略不计。在这一表述中,重点需要理解静力平衡的概念。在实际教学中,一般通过几个具体的例子,来进一步阐述圣维南原理的基本概念。
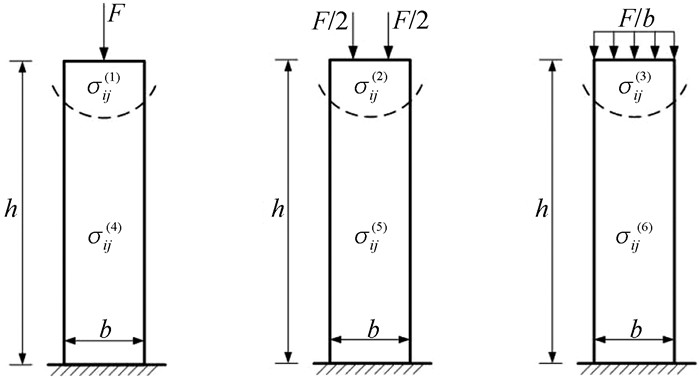
例1,如图 2中3个几何形状、尺寸及材料完全相同的细长悬臂柱,在悬臂端受不同分布的压力作用。虽然3个受压的细长悬臂柱的端部所受力系不同,但它们主矢量均为F,对悬臂端中点的主矩为0的静力等效力系。同时,由于悬臂端是一个小边界,根据圣维南原理,悬臂端附近区域的应力显著不同,即σij(1)≠σij(2)≠σij(3),而其他绝大部分区域的应力几乎相同,即σij(4)≈σij(5)≈σij(6)。
|
图 2 圣维南原理的基本概念:例1 |
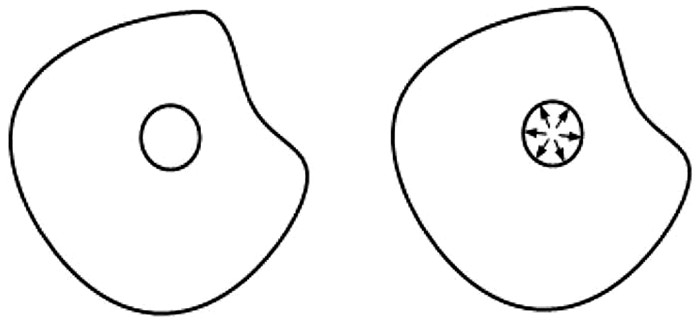
例2,如图 3中两个带小圆孔的无限平面域。右边图在小圆孔周边作用有均布压力,但由于它是一个平衡力系,即主矢量和主矩都等于0的面力,因此,小圆孔附近区域会产生显著的应力,而其他绝大部分区域,将与左边图(小圆孔周边没有任何面力作用)的应力状态相似,接近于无应力状态。
|
图 3 圣维南原理的基本概念:例2 |
从上述两个例子可知,静力等效和静力平衡这两个概念较重要。不仅要明确两者之间的区别与联系,还要清楚如何由这两个概念得到应用圣维南原理解决工程问题的两种基本方法,即静力等效法和静力平衡法。
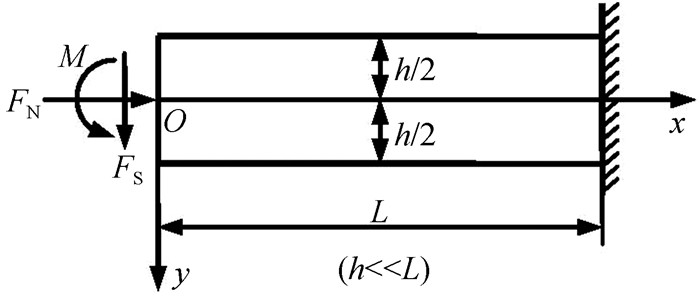
(二) 基本问题在圣维南原理及其应用的基本问题中,通常以图 4所示的等截面矩形梁为例。其中,梁的厚度为1,在局部边界上受主矢量和主矩(这里可以理解为广义面力,区别于分布面力)的作用,思考如何应用圣维南原理建立局部边界的应力边界条件。
|
图 4 基本问题 |
对于基本问题,可以通过两种基本方法来建立应力边界条件,第一种是在局部边界上,首先用假想的分布面力的主矢量和主矩与已知的主矢量和主矩进行静力等效,再利用应力边界条件公式,建立积分的应力边界条件;另一种是在局部边界附近取一微小的脱离体,考虑脱离体的静力平衡条件,进而建立积分的应力边界条件。第一种方法为静力等效法,第二种方法为静力平衡法。教学实践中,基本教学内容中一般仅介绍静力等效法,而将静力平衡法放在具体弹性力学问题的求解中直接应用。这样安排教学内容,不利于学生深刻理解静力等效法与静力平衡法之间的联系与区别,也不利于学生在解决具体问题时思考如何更好地选择求解方法。为此,在实际教学中,将两种方法同时介绍,以展现两种方法的异同点,以便帮助学生灵活应用圣维南原理来建立局部边界的应力边界条件。
事实上,在教学过程中,对于基本问题,只考虑局部边界为坐标面的情况,没有考虑一般的边界面,如斜面或曲面的情况。同时,x坐标轴一般取为梁的轴线,那么,坐标轴不在梁的轴线上应如何建立应力边界条件。上述情况需进行系统阐述。
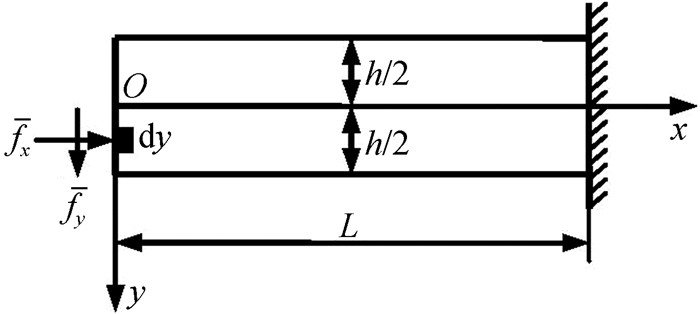
(三) 基本方法 1. 静力等效法首先分析静力等效法。假设在局部边界x=0上作用有分布的面力分量fx(y)和fy(y),如图 5所示。考虑假想的分布面力的主矢量及主矩与已知的主矢量及主矩(广义面力)是静力等效的。于是,得到图 5与图 4在局部边界x=0上的静力等效条件,见式(1)。
| $ \left\{\begin{array}{l} \sum F_x^{(5)}=\sum F_x^{(4)}, \int_{-h / 2}^{h / 2} \bar{f}_x \mathrm{~d} y=F_{\mathrm{N}} \\ \sum F_y^{(5)}=\sum F_y^{(4)}, \int_{-h / 2}^{h / 2} \bar{f}_y \mathrm{~d} y=F_{\mathrm{S}} \\ \sum M_O^{(5)}=\sum M_O^{(4)}, \int_{-h / 2}^{h / 2} \bar{f}_x y \mathrm{~d} y=M \end{array}\right. $ | (1) |
|
图 5 静力等效法 |
利用精确的应力边界条件公式,并考虑局部边界x=0是一个坐标面,其方向余弦为{-1, 0},容易得到假想的面力分量与应力分量的边界值之间的关系,即式(2)。
| $ \left\{\begin{array}{l} \overline{f_x}=l\left(\sigma_x\right)_{x=0}+m\left(\tau_{x y}\right)_{x=0}=-\left(\sigma_x\right)_{x=0} \\ \overline{f_y}=l\left(\tau_{x y}\right)_{x=0}+m\left(\sigma_y\right)_{x=0}=-\left(\tau_{x y}\right)_{x=0} \end{array}\right. $ | (2) |
再将关系式(2)代入静力等效条件式(1)中,即可得到积分的应力边界条件式(3)。
| $ \left\{\begin{array}{l} \int_{-h / 2}^{h / 2}\left(\sigma_x\right)_{x=0} \mathrm{~d} y=-F_{\mathrm{N}} \\ \int_{-h / 2}^{h / 2}\left(\tau_{x y}\right)_{x=0} \mathrm{~d} y=-F_{\mathrm{S}} \\ \iint_{-h / 2}^{h / 2}\left(\sigma_x\right)_{x=0} y \mathrm{~d} y=-M \end{array}\right. $ | (3) |
事实上,积分的应力边界条件就是应力分量边界值的主矢量及主矩与已知的主矢量及主矩之间的静力等效。因此,对于局部边界为坐标面时,也可以直接用应力分量边界值的主矢量及主矩与原问题中的主矢量及主矩进行静力等效,即可得到积分的应力边界条件。可见,对于坐标面边界,直接用应力进行静力等效比面力等效更为简洁方便;但对于一般的局部边界,如斜面、曲面等,则需要用面力进行静力等效。
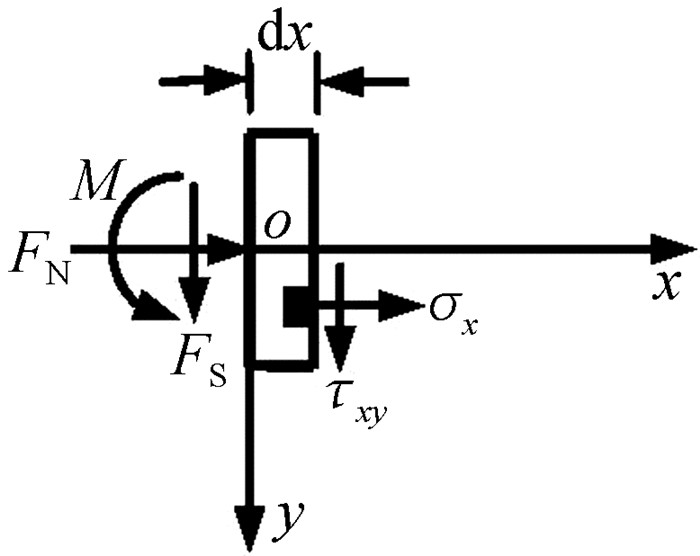
2. 静力平衡法对于静力平衡法,首先在局部边界附近取一微小的脱离体,并暴露出应力分量,如图 6所示。
|
图 6 静力平衡法 |
根据静力平衡条件,得到图 6所示脱离体的静力平衡条件:
| $ \left\{\begin{array}{l} \sum F_x=0, F_{\mathrm{N}}+\int_{-h / 2}^{h / 2}\left(\sigma_x\right)_{x=\mathrm{d} x} \mathrm{~d} y=0 \\ \sum F_y=0, F_{\mathrm{S}}+\int_{-h / 2}^{h / 2}\left(\tau_{x y}\right)_{x=\mathrm{d} x} \mathrm{~d} y=0 \\ \sum M_O=0, M-\int_{-h / 2}^{h / 2}\left(\tau_{x y}\right)_{x=\mathrm{d} x} \mathrm{~d} y \mathrm{~d} x+\int_{-h / 2}^{h / 2}\left(\sigma_x\right)_{x=\mathrm{d} x} y \mathrm{~d} y=0 \end{array}\right. $ | (4) |
最后,令dx→0,即可得到局部边界x=0的应力边界条件式(3)。通过比较式(1)与式(4),可看到静力等效与静力平衡的联系与区别。
在弹性力学的教学实践中,圣维南原理及其应用的基本方法主要包括以图 5为主的静力等效法和以图 6为主的静力平衡法。教科书中也采用了静力平衡法来处理楔形体在尖劈顶端受集中力或力偶作用的问题。为了帮助学生深刻理解圣维南原理的实质,以及掌握在不同局部边界上如何灵活应用圣维南原理,可以对基本问题和基本方法进行延拓,以便更好地理解圣维南原理的内涵,并应用圣维南原理来解决实际工程问题。
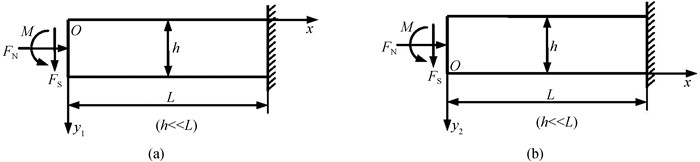
二、基本问题的延拓图 4中,当坐标轴x平移至梁的上、下边界时,如图 7(a)和7(b)所示,则需要考虑如何建立局部边界的应力边界条件。
|
图 7 基本问题的延拓 |
主矢量的静力等效条件(即沿两坐标轴投影的静力等效条件)没有实质性的变化,只需将积分的上下限作相应的改变,而主矩的静力等效条件则需要重新建立。图 7(a)的应力边界条件为式(5),图 7(b)的应力边界条件则式(6)
| $ \left\{\begin{array}{l} \int_0^h\left(\sigma_x\right)_{x=0} \mathrm{~d} y_1=-F_{\mathrm{N}} \\ \int_0^h\left(\tau_{x y}\right)_{x=0} \mathrm{~d} y_1=-F_{\mathrm{S}} \\ \int_0^h\left(\sigma_x\right)_{x=0} y_1 \mathrm{~d} y_1=-M-F_{\mathrm{N}} h / 2 \end{array}\right. $ | (5) |
| $ \left\{\begin{array}{l} \int_{-h}^0\left(\sigma_x\right)_{x=0} \mathrm{~d} y_2=-F_{\mathrm{N}} \\ \int_{-h}^0\left(\tau_{x y}\right)_{x=0} \mathrm{~d} y_2=-F_{\mathrm{S}} \\ \int_{-h}^0\left(\sigma_x\right)_{x=0} y_2 \mathrm{~d} y_2=-M+F_{\mathrm{N}} h / 2 \end{array}\right. $ | (6) |
显然,式(5)和式(6)中的第三式均以坐标原点O来建立主矩的静力等效条件。事实上,只要等式两边都以同一点来建立主矩的静力等效条件即可。此外,若以静力平衡条件来建立上述应力边界条件,也较容易得到相同的结果。
对于基本问题的延拓,还可以直接从基本问题的积分应力边界条件式(3)中,分别利用坐标变换y=y1-h/2和y=y2+h/2,即可得到式(5)和式(6)。
从基本问题的延拓中可以看到,图 7中,虽然局部边界也为坐标面,但坐标轴的位置发生了改变。在实际操作时,学生需要根据变化后的坐标轴应用静力等效条件或静力平衡条件或坐标变换来得到积分的应力边界条件,这对于深刻理解“静力等效”“静力平衡”以及“坐标变换”等概念较有利。
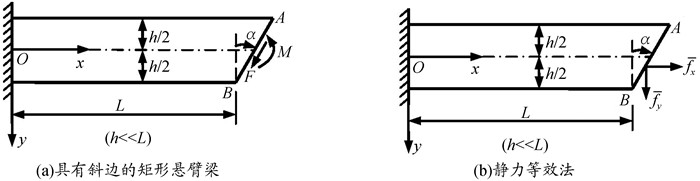
三、基本方法的延拓 (一)静力等效法的延拓图 8(a)所示有斜边的矩形悬臂梁厚度为1,在斜边的中心作用有切向力F和力矩M。应用圣维南原理建立斜边AB的应力边界条件。
|
图 8 静力等效法的延拓 |
显然,案例中的局部边界面是斜面(不是坐标面),应力分量的边界值不能直接给出,因此直接用应力等效较为不便。为此,需要按照面力等效的步骤来建立积分的应力边界条件。
首先,列出局部边界AB的外法线方向余弦l=cosα,m=sinα,并给出边界面的数学表达式。然后,列出局部边界AB上的应力,用假想的面力分量来表示的静力等效条件。应用圣维南原理,在局部边界AB上,图 8(b)与图 8(a)的静力等效条件为:
| $ \left\{\begin{array}{l} \int_A^B-\overline{f_x} \mathrm{~d} s=-F \sin \alpha \\ \int_A^{B-} f_y \mathrm{~d} s=F \cos \alpha \\ \int_A^B\left(\overline{f_x} y+\overline{f_y} y \tan \alpha\right) \mathrm{d} s=M \end{array}\right. $ | (7) |
再利用精确的应力边界条件公式:
| $ \left\{\begin{array}{l} \bar{f}_x=\cos \alpha\left(\sigma_x\right)_s+\sin \alpha\left(\tau_{x y}\right)_s \\ \overline{f}_y=\cos \alpha\left(\tau_{x y}\right)_s+\sin \alpha\left(\sigma_y\right)_s \end{array}\right. $ | (8) |
其中,斜边界s可表示为x=L-(y-h/2)tanα。
将式(8)代入式(7)中,同时,注意到弧微分与坐标微分的变换关系ds=dy/cosα,即可得局部边界AB的积分应力边界条件:
| $ \left\{\begin{array}{l} \int_{-h / 2}^{h / 2}\left[\left(\sigma_x\right)_{x=L-(y-h / 2) \tan \alpha}+\tan \alpha\left(\tau_{x y}\right)_{x=L-(y-h / 2) \tan \alpha}\right] \mathrm{d} y=-F \sin \alpha \\ \int_{-h / 2}^{h / 2}\left[\left(\tau_{x y}\right)_{x=L-(y-h / 2) \tan \alpha}+\tan \alpha\left(\sigma_y\right)_{x=L-(y-h / 2) \tan \alpha}\right] \mathrm{d} y=F \cos \alpha \\ \int_{-h / 2}^{h / 2}\left[\left(\sigma_x\right)_{x=L-(y-h / 2) \tan \alpha}+2 \tan \alpha\left(\tau_{x y}\right)_{x=L-(y-h / 2) \tan \alpha}+\tan ^2 \alpha\left(\sigma_y\right)_{x=L-(y-h / 2) \tan \alpha}\right] y \mathrm{~d} y=M \end{array}\right. $ | (9) |
事实上,对于一般的局部边界,如斜面、曲面等,应用面力的静力等效法来建立其应力边界条件较方便。
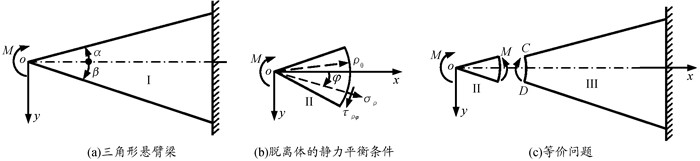
(二)静力平衡法的延拓图 9(a)中三角形悬臂梁厚度为1,在顶端O处受单位厚度的集中力偶M作用,应用圣维南原理建立其应力边界条件。
|
图 9 静力平衡法的延拓 |
对于图 9(a)所示的特殊局部边界问题,采用静力平衡法较方便。在一般弹性力学教科书中[5, 6],大多以坐标原点O为中心,取任意半径ρ0的脱离体,如图 9(b)所示。考虑脱离体的静力平衡条件,得到式(10)。
| $ \left\{\begin{array}{l} \sum F_x=0: \int_{-\alpha}^\beta\left(\sigma_\rho\right)_{\rho=\rho_0} \cos \varphi \rho_0 \mathrm{~d} \varphi-\int_{-\alpha}^\beta\left(\tau_{\rho \varphi}\right)_{\rho=\rho_0} \sin \varphi \rho_0 \mathrm{~d} \varphi=0 \\ \sum F_y=0: \int_{-\alpha}^\beta\left(\sigma_\rho\right)_{\rho=\rho_0} \sin \varphi \rho_0 \mathrm{~d} \varphi+\int_{-\alpha}^\beta\left(\tau_{\rho \varphi}\right)_{\rho=\rho_0} \cos \varphi \rho_0 \mathrm{~d} \varphi=0 \\ \sum M_O=0: M+\int_{-\alpha}^\beta\left(\tau_{\rho \varphi}\right)_{\rho=\rho_0} \rho_0 \mathrm{~d} \varphi \cdot \rho_0=0 \end{array}\right. $ | (10) |
事实上,对于这一特殊的局部边界(局部边界为顶端O处的一点),可以转化为常规的局部边界CD(即ρ=ρ0边界),如图 9(c)所示。只要脱离体II取得微小(即ρ0较小),根据静力等效条件,弹性体III与弹性体I等价,从而弹性体III具有了常规的局部边界CD(即ρ=ρ0边界),其应力边界条件即为式(10)。因此,弹性体III的解答与原问题(弹性体I)的解答相同,根据这一思想,对于变截面矩形悬臂梁则可利用三角形悬臂梁的解答来求解[7, 8]。
对于图 9(a)所示的弹性力学问题,当ρ→0时,其解答出现奇异解,说明在三角形顶端附近处的解答不适用。因此,在满足静力平衡条件时,可将三角形顶端附近的小部分弹性体作“减”处理,而不会对远离三角形顶端弹性体的解答产生影响。
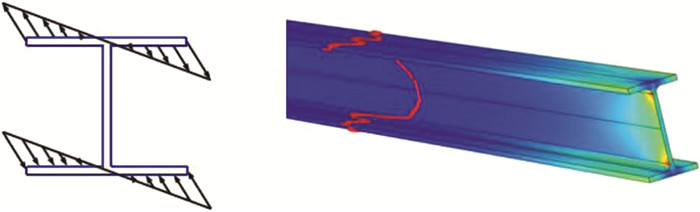
四、基本概念的延拓 (一)工程应用中的注意事项在工程实际中,圣维南原理并不能适用所有的情况,如图 10所示的工字钢受扭矩作用。对于作用在翼缘上的一对力偶,该力偶虽然是一对平衡力系,但距离该力偶较远处的部位依然存在显著的应力。因此,对于壳体、梁和桁架之类的薄壁结构,不能简单按处理“结实”物体的方式来应用圣维南原理。因为薄壁结构内的载荷路径较少,所以扰动传播的距离较远。
|
图 10 工字钢受扭矩作用 |
这个例子表明,当荷载作用区域大于物体受力处截面组成部分的最小尺寸时,圣维南原理无效。如果双力偶同时作用在腹板上,且双力偶的力臂小于腹板厚度,圣维南原理仍然有效。因此,在应用圣维南原理时应当具体问题具体分析。
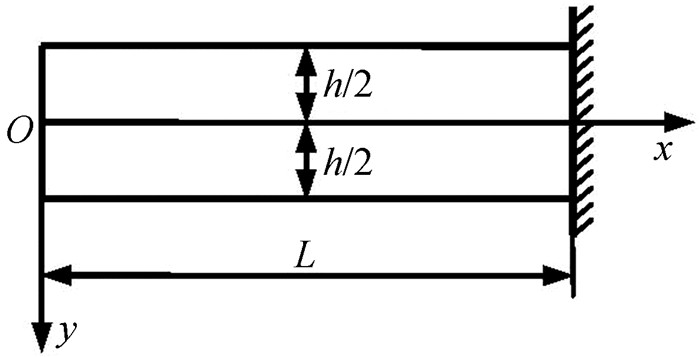
(二)对位移边界条件的启发尽管圣维南原理主要针对应力边界条件,事实上,其基本思想对于局部边界上的位移边界条件也有重要的借鉴意义,例如图 11中悬臂梁固定端位移边界条件的近似表达。固定端精确的位移边界条件可由函数方程式(11)表达。
|
图 11 位移边界条件 |
| $ \left\{\begin{array}{l} \left.u(x, y)\right|_{x=L}=u(L, y)=0 \\ \left.v(x, y)\right|_{x=L}=v(L, y)=0 \end{array}\right. $ | (11) |
该方程在实际工程中往往不易满足。此时,需要用近似的位移边界条件来替代,即式(12)。
| $ \left\{\begin{array}{l} \left.u(x, y)\right|_{x=L, y=0}=0 \\ \left.v(x, y)\right|_{x=L, y=0}=0 \\ \left.\frac{\partial v}{\partial x}\right|_{x=L, y=0}=0 \end{array}\right. $ | (12) |
显然,近似的位移边界条件是代数方程,可简化问题的求解。
可见,近似的位移边界条件与积分的应力边界条件,或者与近似的应力边界条件具有异曲同工的效果,这是圣维南原理基本思想的具体体现。最后,总结归纳应力边界条件和位移边界条件,见表 1。
| 表 1 精确的边界条件与近似的边界条件对比 |
开展探究式教学是提高高等学校教育教学质量的途径之一。探究式教学重在鼓励学生“在学习中研究,在研究中学习”,鼓励学生不要仅仅满足于教材中的基本教学内容和知识,要研究和挖掘基本教学内容的深度。通过在教学过程中给学生提供基于课程教学内容而又略高于课程教学内容的问题,这些问题可以是基于教学内容的延伸和扩展,也可以是与工程实际有关的问题,还可以是力学建模问题,激励学生敢于质疑、善于专研、勤于思考的品质,使学生初步具备研究能力和一定的科学素养。
弹性力学是固体力学的分支,主要研究弹性体在外力、位移约束或温度变化等外界因素下所产生的应力、应变和位移,从而解决各类工程中的强度、刚度和稳定问题。在弹性力学课程教学中,以圣维南原理及其应用这一基本教学内容为例,深入开展了探究式案例教学的设计与实践。在基本教学内容的基础上,通过对圣维南原理的基本概念,以及圣维南原理应用的基本问题和基本方法进行深入阐述与延拓,并进一步结合工程实践,探讨了在不同的局部边界上如何有效理解和灵活应用圣维南原理。教学实践表明,探究式教学有助于学生更加深刻地领悟力学原理的实质及实践应用,能够极大地提高学生的学习兴趣和钻研精神。学生的学习效果和学习成绩显著提高,探究式教学值得在教学中推广应用。
| [1] |
易红郡, 张燕. 剑桥大学本科生研究性教学体系的构成、特征及启示[J]. 青岛科技大学学报(社会科学版), 2020, 36(3): 100-105. |
| [2] |
范钦珊, 陈建平, 蔡新, 等. 研究型大学需要研究型教学: 力学课程研究型教学的几点体会[C]//力学课程报告论坛2008论文集. 北京: 高等教育出版社, 2009, 24-27.
|
| [3] |
梅群, 梁斌, 徐红玉, 等. 弹塑性力学课程教学改革研究[J]. 洛阳理工学院学报(自然科学版), 2015, 25(2): 93-96. |
| [4] |
刘章军, 吴勃, 卢海林. 弹性力学与有限元基础[M]. 北京: 高等教育出版社, 2019: 30-35.
|
| [5] |
徐芝纶. 弹性力学简明教程[M]. 北京: 高等教育出版社, 2002.
|
| [6] |
吴家龙. 弹性力学[M]. 北京: 高等教育出版社, 2001.
|
| [7] |
刘章军. 弹性力学内容精要与典型题解[M]. 北京: 中国水利水电出版社, 2009: 77-85.
|
| [8] |
刘章军, 叶永, 周宜红, 等. 用楔形体解答求解矩形变截面梁及其适用范围[J]. 力学与实践, 2012, 34(2): 71-74. |
 2022, Vol. 31
2022, Vol. 31


