体系的几何组成分析是结构力学课程的重要组成部分。一方面,通过体系的几何组成分析,可确定体系的几何构造是否合理、承受荷载时是否能保持几何形状不变。另一方面,几何组成分析和结构的内力分析关系密切,在结构受力分析和计算时进行几何组成分析有助于选择正确的计算方法和简捷的解题途径[1]。对学生来说,此章节的内容和分析方法比较独立,且概念性、技巧性较强,属于结构力学课程开篇的难点。关于体系几何组成分析规则的理解和分析技巧、瞬变体系分析等,鲁彩凤等[2-6]进行了专门研究并分享了教学经验。在传统教学过程中,教师重点对几何组成规则、分析技巧进行讲解,但在学生作业和测验的非难题中仍有不少错误。通过分析发现,学生对几何组成分析中一些关键概念的理解并不透彻,从一定程度上影响了学生对几何组成规则的应用和几何组成分析方法的掌握,这些问题如不能有效解决将对后续结构内力分析方法学习产生不利影响[7]。为加强学生对几何组成分析相关概念的理解,教学过程中使用了变式教学法,重点对几何组成分析的几个关键概念进行多角度解释,以帮助学生理解概念,从而能够更合理、更准确地应用几何组成分析规则和技巧。
一、结合图示的变式教学法 (一) 变式教学法“变式”教学[7]是指,在教学中用不同形式的直观材料或事例说明事物的本质属性,或变换同类事物的非本质特征以突出事物的本质特征。目的在于使学生了解事物的本质特征和非本质特征,从而对事物形成科学概念。
在中国,变式教学法较早运用于概念的教学。在20世纪80年代,学者结合数学教学实践对变式教学进行了系统、深入的实验研究与理论分析[7-9]。研究表明,概念性变式有助于学生准确把握思维技能方法。概念性变式是依托变异理论,通过对概念的多角度理解促进对概念的确切掌握,可分为概念变式和非概念变式[10]。“概念”是人类在认识事物的过程中,把所感知的事物的共同本质特点抽象出来并加以概括,形成概念式思维惯性。在概念描述中,必然会包含某一个或多个表示共同特点的部分,这些共同特点是判别本概念的重要依据,可称为“关键特征”。相应地,可将不属于“关键特征”的其他特点成为“非关键特征”。概念变式是指关键特征不变而非关键特征改变的变式,用来引入概念和突出概念的本质属性。非概念变式则是关键特征改变的变式,用来解释概念的对立面从而明确概念的外延[7]。图 1为数学中“圆的直径”的概念性变式示例。其中,基本概念中包含“通过圆心”和“两个端点在圆周上”这两个关键特征,对应的典型形式给出了最常见的直径图示。非概念变式是不满足其中一个关键特征的错误示例,包括不通过圆心和不是两个端点都在圆周上的情况。而概念变式为非关键特征的变化,即直线虽然不是水平直线、竖直或斜向,但在满足过圆心和两个端点都在圆周上的情况下仍是圆的直径。
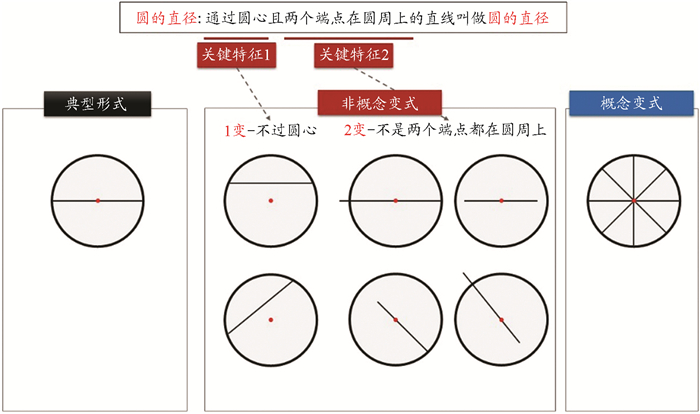
|
图 1 概念性变式的示例 |
概念性变式引入直观或具体的变式,可建立感性经验与抽象概念之间的联系。通过概念变式可突出概念的本质属性,通过非概念变式使概念的内涵更加明确、外延更加清晰。尽管变式教学源于数学教学,但其思维方法也适用于物理、化学、力学等自然科学学科。变式教学形式上是在对知识进行有层次的深入加工,在获得知识的同时提升了知识加工的能力和思维能力。通过变式教学,可促进思维技能迁移,其中的概念性变式有助于学生对思维技能方法的准确、透彻把握。
(二) 知识可视化知识可视化是用来构建、传达和表示复杂知识的图形、图像手段。应用知识可视化可以在传输知识的过程中帮助学生正确地重构、记忆和应用知识。知识可视化常利用图像或图示来提高知识的有效传播,从而提高学生学习效率。它的实质是将内隐知识或隐性知识外显化,将外显知识生动化。文字和图示是两种本质不同的知识表征系统。从心理学上看,若仅用文字这种较抽象的方式描述一种概念,并不利于学生对知识的理解。而通过图示将知识可视化,可以更直观、更具体地让学生通过视觉形式来理解事物,因为图画是人类表征知识最原始的模式,人类通过视觉接收的知识占80%以上。
在结构力学教材中,介绍一个新的概念时,往往会在语言文字表述的同时也给出对应的图示,这有助于学生理解初次接触的概念。然而,教材中一些较抽象、特征较多的概念仅有一种典型图示,可使学生浅层次的了解概念,并不能保证学生对其他符合概念特征的非典型图示的理解与应用。因此,结合概念的变式教学法特点,提供与概念变式和非概念变式的文字说明相对应的各种图示,可以在应用新的概念进行几何组成分析之前就向学生展示出不同情况的概念应用,更有效的向学生传达知识,便于学生对新概念的记忆和理解。
(三) 认知负荷理论认知负荷是表示处理具体任务时加在学习者认知系统上的负荷多维结构。根据认知负荷理论,工作记忆是信息加工的唯一场所,其容量小,只能同时存储7个或加工2~3个信息单元[11-12]。认知负荷主要包括三类,即内在认知负荷、外在认知负荷和相关认知负荷。内在认知负荷是指工作记忆对认知任务本身所包含的概念或规则等基本成分信息元素的数量及其交互性进行认知加工活动所产生的负荷。当在工作记忆中同时加工处理的信息单元越多时,产生的内在认知负荷就越高。外在认知负荷是指超越内部认知负荷的额外负荷,主要为信息的呈现方式不当增加的负荷部分。如果采用了不恰当、不合理的教学设计,会导致学习者发生与认知加工过程没有直接关联的活动,从而施加给工作记忆不必要的负荷,这属于外在认知负荷。一般认为前两类认知负荷不能促进图式构建或认知形成,属于无效认知负荷。相对而言,相关认知负荷则是有效认知负荷,指的是工作记忆对认知任务进行实质性认知操作而承受的负荷,用于知识的重组、抽象、比较和推理等更高级有意识地认知加工。
结构力学教学过程中,教学设计应以提高学生的认知效率为准则,有效管理三种认知负荷,合理科学降低内在和外在认知负荷,提高相关认知负荷,使学习者所承受的三种负荷之和不超过其工作记忆的总负荷。在介绍体系几何组成分析的相关概念时,新的概念往往与先修课程中的概念有密切关系,但又存在新的要求或特征,教学中应使学习者充分理解并强调新概念中的重要特征。理解新概念中的重要特征并学会应用概念分析问题的负荷,属于内在认知负荷。为便于学习者理解概念,课堂教学中除了对概念进行文字描述,还辅以图片呈现,再加上教师的讲解,包括了多种呈现方式,需要合理设计课件和讲授过程才能保证不过多地增加外在认知负荷。在教学过程中达到教学目标的关键在于如何增加相关认知负荷。
变式教学法在介绍概念、展示关键特征的同时,给出概念的外延和内涵,可有效帮助学生辨析概念的本质属性;同时,教学中科学应用图示、利用知识可视化、提供变式概念和非变式概念的图示,可使学生更容易理解教学内容,能增加学生学习过程中的相关认知负荷。变式教学法在介绍典型形式的同时,需要学习者了解其对应的概念变式和非概念变式的相关内容,会使内在认知负荷有所升高。但只要增加的变式教学内容能使学习者通过自动化提取已经掌握的长时记忆内容,可以在增加相关认知负荷的同时使得内在认知负荷增加的压力控制在有限范围内,从而有效降低总的认知负荷。总之,结合图示的变式教学法可以使学生学习新的力学概念时降低工作记忆的负荷,从而帮助学生提高学习效率、掌握新知识。
二、体系几何组成分析的问题及原因分析结构力学课程中,体系的几何组成分析包含较多抽象的力学概念,如几何可变体系、几何不变体系、刚片、体系的自由度、不同类型的约束等。有些概念是在理论力学和材料力学课程中要求学生熟练掌握的,有些则属于课程出现的新概念。在本单元的传统教学过程中,通常以几何组成规则、规则应用的技巧和注意问题为重点讲授内容,对出现的新概念一般不作过多的讲解和针对练习。但从学生作业或考试相关情况来看,不少学生对虚铰、铰结三角形和二元体等新概念的理解存在问题,导致规则应用或分析过程出现错误。部分学生作业的错误示例见表 1。
| 表 1 学生作业错误示例 |
认知心理学的图式理论认为,人们根据先前反应或经验进行积极组织,促使头脑中存在对外在事物的结构性认识,这种存在于记忆中的认知结构或知识结构称为图式。图式包括对所认识的对象特点以及相互关系的认识,这种认识是对反复出现的情况概括认识,省略了细节而概括了一些相似情况的共同特点[13-14]。简单地说,图式是对一个整体的抽象。
结构力学课程中,学生对虚铰、二元体、铰结三角形等概念的学习和理解,就是在学习者脑中形成图式的过程。要使学生真正理解这些概念,形成图式,就必然经过辨识每个概念中的细节和关键特征,并通过与其他不符合关键特征的对象进行对比分析的学习过程。最终,在学生大脑中形成一种可重复的认知模式或结构单元,即为图式。图式的形成,可以帮助学生建立一种模块化、自动化且稳定的认知过程,这种通过大脑分析、记忆编码形成稳定的知识属于记忆中的“长时记忆”。简单地说,一旦图式形成即可建立一个概念的长时记忆,学生再次遇到这个概念时大脑会自动或流程式地找到对应图式,并快速作出判断。但是,图式在没有“自动化”之前是不稳定的,需要通过变换情境使学习者加强学习。一般情况下,仅学习教材上的概念,多数学生并不能形成稳定的图式,这种不稳定体现为表 1中学生作业中常见的错误题目。
因此,结合变式教学法的特点,作者在教学过程中将概念性变式引入体系几何组成分析相关概念的讲解,以帮助学生形成稳定的图式,从而更加全面、准确的理解这些概念。
三、体系几何组成分析的概念性变式教学 (一) 虚铰的概念性变式虚铰概念:两根不相连的链杆构成的两刚片之间的连接叫虚铰。这个概念包括必须满足的3个关键特征,即“两根”“不相连”“两刚片之间的连接”。根据概念,虚铰的典型形式、非概念变式和概念变式如图 2所示。
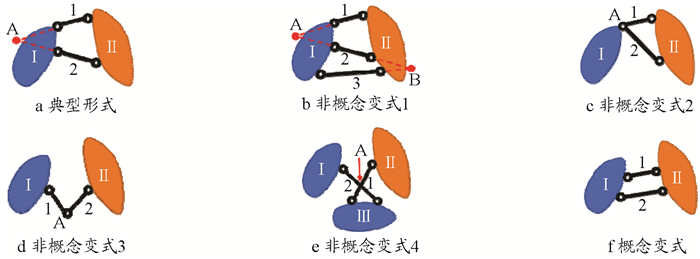
|
图 2 虚铰的概念性变式 |
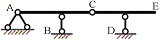
根据概念,对图 2a中虚铰的典型形式进行说明:刚片Ⅰ和Ⅱ之间由链杆1和2连接,且链杆1和2不相连,则A为连接刚片Ⅰ和Ⅱ的虚铰。
根据虚铰概念的3个关键特征,分别给出不满足某一个关键特征时的非概念变式,如图 2b—图 2e所示,并分别结合各关键特征的变化情况进行说明。非概念变式1不满足“两根链杆连接”刚片的情况,如图 2b所示,刚片Ⅰ和Ⅱ由3根链杆连接,则连接Ⅰ和Ⅱ的是虚铰A和链杆3,或虚铰B和链杆1,不能认为是两个虚铰或仅有一个虚铰。非概念变式2不满足“两根链杆不相连”的情况,如图 2c所示。链杆1、2连接在一起(交于点A),则连接刚片Ⅰ和Ⅱ的是实铰A,不是虚铰。非概念变式3和非概念变式4不满足“两刚片之间的连接”的情况,如图 2d、2e所示。其中,图 2d中链杆1和2不是刚片Ⅰ和Ⅱ之间的(直接)连接,则A不是虚铰;图 2e中链杆1连接刚片Ⅰ、Ⅱ,链杆2连接刚片Ⅰ、Ⅲ,不是两个相同刚片之间的连接,两根链杆不是两个刚片之间的连接,则A不是虚铰。
最后,图 2f是虚铰的概念性变式。刚片Ⅰ和Ⅱ之间由链杆1和2连接,链杆1和2平行,交点A在无穷远处,则连接刚片Ⅰ和Ⅱ的虚铰A在无穷远处。虽然和典型图示存在不同之处,但3个关键特征完全满足,属于虚铰。
(二) 铰结三角形的概念性变式铰结三角形概念:三根链杆由不共线的三个铰两两连接,组成的体系为铰结三角形。这个概念包括必须满足的3个关键特征,即“三根链杆”“不共线”“三个铰两两连接”。根据概念,铰结三角形的典型形式、非概念变式和概念变式如图 3所示。
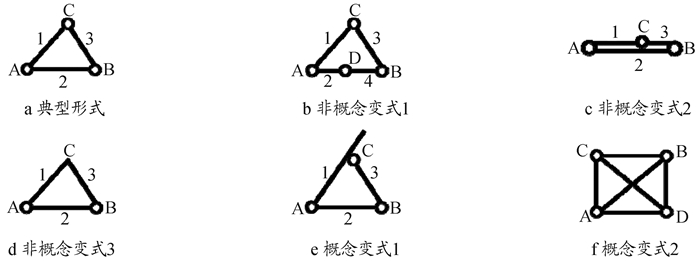
|
图 3 铰结三角形的概念性变式 |
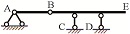
根据概念,对图 3a中铰结三角形的典型形式进行说明:链杆1、2、3由3个铰两两连接,其中铰A连接1和2,铰B连接2和3,铰C连接1和3,且三个铰不共线,则三角形ABC为铰结三角形。
根据虚铰概念的3个关键特征,分别给出不满足某一个关键特征时的非概念变式,如图 3b-3d所示,并分别结合各关键特征的变化情况进行说明。非概念变式1不满足“三根链杆”的情况,如图 3b所示,4根杆由4个铰连接,即使AD、BD共线,看似形成三角形图形,但三角形ABC不是铰结三角形。非概念变式2不满足“不共线”的情况,如图 3c所示,铰A、B、C在一条直线上,三角形面积蜕化为零,这时图形ABC不是铰结三角形。非概念变式3不满足“三个铰两两连接”的情况,如图 3d所示,杆件1、3之间是由刚结点C连接的,则三角形ABC不是铰结三角形。
最后,图 3e、3f给出的是铰结三角形的概念性变式。图 3e中,杆1和3由铰C连接,虽然铰C不在杆1的端部,三角形ABC仍可认为是铰结三角形。图 3f中,三角形ABC已经满足铰结三角形的3个关键特征,这时,如果还有其他杆件与铰结三角形的某一个或多个铰相连,则三角形ABC仍是铰结三角形。
(三) 二元体的概念性变式二元体概念:两根链杆(夹角不是180°)一端用铰连接、另一端与其他部分连接的构造,称为二元体。这个概念包括必须满足的4个关键特征,即“两根链杆”“夹角不是180°”“用铰连接”“另一端与其他部分连接”。根据概念,二元体的典型形式、非概念变式和概念变式如图 4所示。
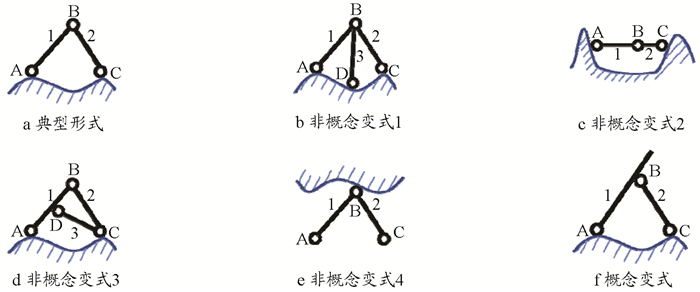
|
图 4 二元体的概念性变式 |
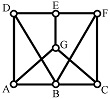
根据概念,对图 4a中二元体的典型形式进行说明:链杆1、2由铰B连接,另一端与其他部分连接的体系,且∠ABC≠180°,则构造ABC为二元体。
根据虚铰概念的4个关键特征,分别给出不满足某一个关键特征时的非概念变式,如图 4b-4e所示,并分别结合各关键特征的变化情况进行说明。非概念变式1不满足“两根链杆”的情况,如图 4b所示,铰B连接了链杆1、2、3共计3根杆,则构造ABC不是二元体。非概念变式2不满足“夹角不是180°”的情况,如图 4c所示,杆1、2由铰B连接,但∠ABC=180°,则构造ABC不是二元体。非概念变式3不满足“一个铰连接”的情况,如图 4d所示,链杆1、2除了由铰B连接,还有一根杆3与杆1和2连接,则构造ABC不是二元体。非概念变式4不满足“另一端与其他部分连接”的情况,如图 4e所示,杆1、2通过在B端铰结,且在B端与其他部分连接,则构造ABC不是二元体。
最后,图 4f为二元体的概念性变式。图 4f中,链杆1和2由铰B连接,另一端与其他部分连接的体系,虽然铰B不在杆1的端部,构造ABC仍是二元体。
(四) 变式教学效果分析体系几何组成的上述概念对应的典型形式一般是教材中普遍在介绍概念后给出的典型示意图,也是学生最直接记忆或理解的概念典型形式,如果体系分析中出现这种典型图示,学生一般都能正确判断。由于体系的形状和杆件组成方式多种多样,学生在具体题目中遇到的往往不是概念介绍时的典型形式,如果没有理解概念的内涵和外延,经常会出现概念性错误,影响体系几何组成分析规则的应用,进而导致结果错误。以往教学经常在学生作业或测试题中出现错误后,在作业讲解或习题课上进行教学反馈,从认知规律看,不利于知识的掌握。为使学生在学习概念初期就能形成完整深入的理解,可在总结常见错题的基础上,采用变式教学法教授概念,详细介绍满足概念要求的其他形式、给出非概念变式和概念变式的图示,以增强学生对新概念的理解。将概念性变式引入几何组成分析一章的教学后,学生作业和考试的错误有所减少。为分析教学效果,作者在学期末的教学内容掌握情况调查中对学生掌握体系几何组成分析一章的情况进行了调研,要求学生对本章知识点的掌握程度进行主观评分,总分为5分。不同学年、不同方法的土木工程专业本科学生学习效果评价如图 5所示。其中,变式教学法为2020年线上、线下混合教学中初次采用变式教学法的学习效果评分。常规教学1、2、3分别为2020年线上、线下混合教学中2019年和2018年在线下教学中采用常规教学法的学生学习效果评分。
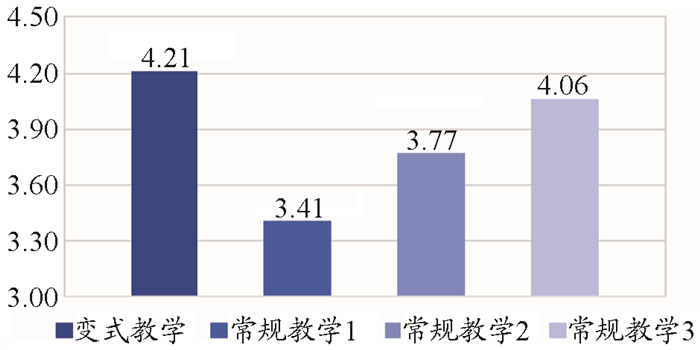
|
图 5 不同教学方法的学生学习效果评分对比 |
从图 5数据可看出,2020年虽然教师首次采用线上、线下混合教学方法进行结构力学课程授课,由于应用了变式教学法,本章知识点掌握程度评分为4.21,高于采用常规方法教学后的评分,也高于2020年其他未采用变式教学法授课的学生评分,表明该方法有利于学生对几何组成分析相关知识点的掌握。
四、结语源于数学教学的变式教学法也适用于结构力学课程教学。在体系几何组成分析部分课堂教学中,利用概念性变式对出现的新概念进行讲授,可以帮助学生在概念学习初期多角度、全方位地理解其本质,预防可能出现的概念错误或混淆,促进学生正确、合理地应用几何组成规则完成体系分析。同时,概念性变式教学,也有利于发展学生独立概括概念特征的思维能力,可在结构力学教学中推广应用。
| [1] |
赵均海, 王新华, 贾红英. 结构力学(上册)[M]. 北京: 化学工业出版社, 2010.
|
| [2] |
王建祥, 胡景龙, 陈国新. 平面体系机动分析模式及其应用[J]. 高等建筑教育, 2017, 26(3): 62-65. |
| [3] |
鲁彩凤, 鲁凤弟. 从几何组成分析中找到结构内力分析的方法[J]. 高等建筑教育, 2012, 21(5): 101-104. |
| [4] |
袁全, 袁驷, 李易, 等. 几何可变体系大变形机构模态的二元体构建法[J]. 力学与实践, 2018, 40(5): 510-513, 519. |
| [5] |
郇筱林, 王崇革. 平面体系几何组成规则的理解和简化分析技巧[J]. 力学与实践, 2018, 40(6): 696-699. |
| [6] |
张琳楠, 徐春晖, 秦太验. 平面体系机动分析的一般方法[J]. 力学与实践, 2014, 36(6): 738-741. |
| [7] |
鲍建生, 黄荣金, 易凌峰, 等. 变式教学研究[J]. 数学教学, 2003(1): 11-12. |
| [8] |
鲍建生, 黄荣金, 易凌峰, 等. 变式教学研究(续)[J]. 数学教学, 2003(2): 6-10, 23. |
| [9] |
鲍建生, 黄荣金, 易凌峰, 等. 变式教学研究(再续)[J]. 数学教学, 2003(3): 6-12. |
| [10] |
赵国庆, 熊雅雯, 王晓玲. 思维发展型课堂的概念、要素与设计[J]. 中国电化教育, 2018(7): 7-15. |
| [11] |
赵立影, 吴庆麟. 基于认知负荷理论的复杂学习教学设计[J]. 电化教育研究, 2010, 31(4): 44-48. |
| [12] |
唐剑岚, 周莹. 认知负荷理论及其研究的进展与思考[J]. 广西师范大学学报(哲学社会科学版), 2008, 44(2): 75-83. |
| [13] |
赵慧臣. 知识可视化的视觉表征研究综述[J]. 远程教育杂志, 2010, 28(1): 75-80. |
| [14] |
康立新. 国内图式理论研究综述[J]. 河南社会科学, 2011, 19(4): 180-182. |
 2023, Vol. 32
2023, Vol. 32