一、研究钢筋混凝土结构设计原理课程教学方法的必要性

土木工程不仅仅是一个专门的学科，还是人类文明、文化、历史、技术、经济的载体。混凝土结构是现代土木工程结构最主要的结构形式，已广泛应用于工业和民用建筑等领域，它的安全可靠性关系着国计民生。钢筋混凝土构件力学性能独特的变化使得从其出现至今已发展成为土木工程结构中最重要的学科。钢筋混凝土结构设计原理不仅是混凝土结构学科的主干课程，而且是土木工程专业的一门专业必修课，也是该专业学时最多的一门课程。

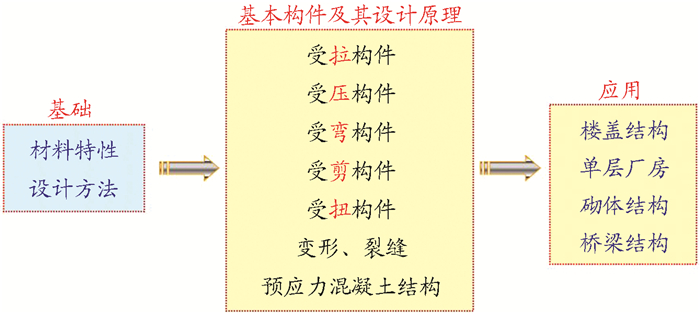
钢筋混凝土结构设计原理以理论力学、材料力学、弹塑性力学、结构力学、概率论与数理统计理论，以及土木工程材料等基础课程理论为基础，综合利用所学的力学基本理论、结构设计基本知识和方法，通过建立合理的力学模型并进行详细准确的计算分析，完成对结构体系和构件的设计，并通过图纸展现出来，它所包含的理论知识(图 1所示)、学习方法和思维方式是学习钢筋混凝土结构设计、砌体结构、桥梁工程、基础工程等后续专业课程的基础^[1-7]，是从基础课向专业课过渡的重要课程。

钢筋混凝土结构设计原理的许多理论都是建立在科学实验和工程经验基础之上，采用了许多基本假定，具有半理论、半经验、答案不唯一、概念多、内容多、符号多、公式多等特点，学习难度相对较大，加之该课程实践性较强，与实际工程设计联系紧密，急需教师研究一种可以提高教学质量的行之有效的教学方法。

二、钢筋混凝土结构设计原理课程的主要内容及蕴含的哲学思想

由图 1可知，钢筋混凝土结构设计原理主要内容包括：(1) 钢筋和混凝土材料的力学性能分析；(2)钢筋混凝土结构设计与基本假定；(3)钢筋混凝土梁的受弯分析与设计；(4)钢筋混凝土梁中的剪切和斜向受拉，以及斜截面抗剪分析与设计；(5)钢筋混凝土构件的构造分析，如黏结、锚固及延伸长度；(6)素混凝土构件与钢筋混凝土构件的受扭分析与设计；(7)钢筋混凝土短柱受压分析与设计；(8)钢筋混凝土细长柱受压分析与设计；(9)钢筋混凝土柱受拉分析与设计；(10)钢筋混凝土构件的适用性分析，如裂缝分析和挠度分析；(11)预应力钢筋混凝土构件的力学性能分析与设计；(12)设计原理在混凝土结构设计中的应用，如楼盖结构、单层厂房、砌体结构、桥梁结构及组合结构等。

该课程主要涉及材料、构件、结构的分析与设计，内容较多。在教学和学习过程中，要将理论分析与工程实际相结合，从简单分析向复合分析转变；将基础知识与工程创新相结合；将科学的经验与理论、工程概念及实践性(如试验与实施等)相融合，采取灵活的教学方式帮助学生加深对课程内容的理解和应用。

三、拓展钢筋混凝土结构设计原理课程教学内容的必要性

创新是发展的灵魂，创新驱动发展。钢筋混凝土结构设计原理课程主要内容的更新经历了不断创新的实践过程。贝叶斯思维方法是基于贝叶斯理论公式分析得到的。贝叶斯公式包含研究变量的先验分布信息、研究变量的似然函数信息，以及研究变量的后验分布信息三部分。钢筋混凝土结构设计原理课程中研究变量一般指梁正截面受弯承载能力、梁斜截面受剪承载能力、梁受扭承载能力, 以及柱的受压和受拉承载能力等。影响这些研究变量的随机变量很多，如截面尺寸、混凝土强度、钢筋强度等。这些随机变量的概率分布均已知，按照混凝土结构设计原理的相关公式，研究变量可由上述随机变量进行表达，进而利用数值模拟方法可以得到研究变量的先验分布信息。研究变量的似然函数信息可以通过梁以及柱等构件的服役信息来获取，进而结合贝叶斯公式即可得到研究变量的后验分布信息。研究变量的先验信息是基于经验设计公式和数值模拟方法得到的，具有较强的主观性。采用贝叶斯公式将构件的服役信息和先验信息融合，得到的后验信息可以降低研究变量的主观性，使其更符合实际情况。

由上述可知，贝叶斯思维方法可以提高人们对客观事物认知能力，减少对事物的主观认识，实现对客观事物的逐渐加深。混凝土学科发展过程中渗透着贝叶斯思想，如：钢筋混凝土结构设计规范从经验规范到半经验规范，最后到基于随机概率论的结构设计规范，这个演变过程，体现了人们更加客观地认识客观事物，不断降低人为的主观认识水平，这是科技和文化属性不断进步的特征。

钢筋混凝土结构设计原理是土木工程专业的专业基础课程，具有理论与工程实践相结合的特征，课程的掌握程度很大程度上影响其他专业课的学习和掌握；因此，努力学习并拓展相关主要内容，可以提高学生的专业素养。

四、本体论的哲学概念和本体模型的建模过程 (一)本体论的基本理论

本体论的定义在哲学领域一直存有争论。在马克思主义出现之前，哲学上对于本体论的定义有广义与狭义的区别，在马克思主义出现后，本体论开始融入实践之中。从广义上说，本体论是世界的最终本性，这种本性需要通过认识论来认知。因此，在广义本体论的定义上，一般将本体论与认识论相结合，通过比较它们的区别来定义本体论。本体论是一切事物的最终本性，需要认识论来认识它，因此，本体论与认识论是对偶的存在。从狭义上说，世界一切又分为世界的起源和世界的本性两个方面。世界的起源为宇宙论，而世界的本性为本体论。因此，本体论与宇宙论是对偶的存在。

马克思主义哲学认为，物质为世界的起源，限定了宇宙论的观点。马克思主义哲学既不采取认识论与本体论对偶存在，又不采取宇宙论与本体论对偶存在，而是坚持以唯物辩证法解释所有问题。

综上可知：本体论是客观事物的最终本性，这种本性需要通过认识论来认知。因此，一般将本体论与认识论相结合，通过比较来定义本体论。总体而言，本体论是一切事物的最终本性，而最终本性需要认识论来认识它，因此，只有不断地实践和认识，才能对客观现象的本质(或本体)进行合理的认识和掌握。

(二)本体模型的建模过程 1. 本体论的意义

(1) 理解层面：本体论概念已深入具体的基础学科中，如：信息科学技术、人工智能、工程技术等。通过探究本体论的构造、本质、作用，进一步深化对本体论的研究，以更好地规范对本体论的运用，使本体论的具体科学应用有更明确的方向和更可靠的学理基础，从而使之更健康地向前发展。

(2) 应用层面：本体论作为一个哲学概念，是研究本质的哲学思维。本体论可以将影响本体的因素融合起来，反映本体的本质特性，从而能构建和人类一样的智能系统，并应用于土木工程领域。

2. 构件本体模型

基于本体论的基本理论建立客观事物的本体模型：(1) 结合认识论，详细列出本体模型所涉及的词条；(2) 结合认识论，建立各词条之间的关系；(3) 给出最终本体模型的精细化关系。

五、基于本体模型的钢筋混凝土结构设计原理课程教学方法研究

钢筋混凝土结构设计原理课程的教学内容较多，其中承载能力的计算分析教学内容主要包括：钢筋混凝土梁正截面受弯承载能力分析、钢筋混凝土梁斜截面抗剪承载能力分析、钢筋混凝土梁受扭承载能力分析、钢筋混凝土柱抗压承载能力分析、钢筋混凝土柱抗拉承载能力分析等。通过认识论，建立部分教学内容的本体模型，给出可广泛普及的行之有效的教学方法。

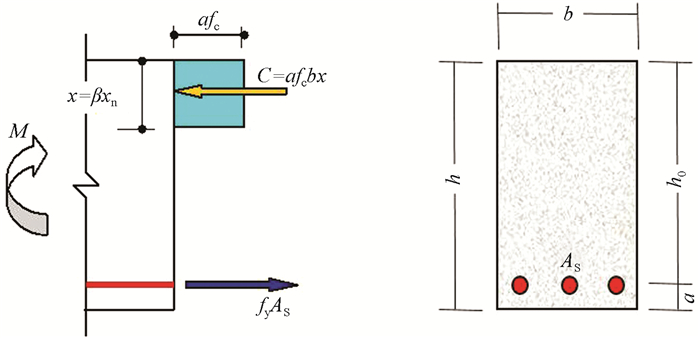
(一)适合于截面复核的钢筋混凝土梁正截面受弯承载能力本体模型

采取单筋矩形截面梁(图 2所示)建立对应的本体模型。图 2中h为截面高度；h₀为截面有效高度；A_S为受拉钢筋面积；b为截面宽度；a为钢筋形心到截面受拉边缘的距离；M为设计弯矩；α与β是由混凝土应力-应变本构曲线得到的特定型号混凝土的等效矩形图形系数；x为简化的受压区高度；x_n为实际受压区高度；f_c为混凝土强度设计值；f_y为钢筋强度设计值。

(1) 准确认识单筋截面梁试验过程中受拉区混凝土拉裂、受拉区钢筋屈服及受压边缘混凝土压碎三个阶段的特征，三个阶段对应的弯矩值分别为开裂弯矩、屈服弯矩及极限弯矩。极限弯矩即受弯承载能力本性值，极限状态下受拉区混凝土的抗拉性能不予考虑。截面极限弯矩与截面的惯性矩相关，因而在词条里包括极限状态下受压区截面的尺寸(b、x_n)。截面极限弯矩与钢筋与混凝土的材料破坏相关，因而在词条里包括f_c与f_y。结合试验梁的破坏现象、混凝土和钢筋的应力应变曲线、极限状态破坏的破坏特征，为了得到简化的计算方法，引入α与β作为词条。

综上可知，受弯承载能力本性值涉及词条包括h、h₀、A_S、b、a、M、α、β、x、x_n、f_c以及f_y。

(2) 由图 2可知，通过截面力的平衡表达关系式式(1)和弯矩平衡表达关系式式(2)可将上述各词条联系起来，

$\alpha f_c b \beta x=f_y A_s$

(1)

$M \square M_u=\alpha f_c b \beta x\left(h_0-\frac{\beta x}{2}\right)=f_y A_s\left(h_0-\frac{\beta x}{2}\right)$

(2)

(3) 通过(2)的详细计算分析，得到单筋矩形截面梁的受弯承载能力本体模型或本性值M_u，以便于后续的截面复核。

由上述分析可知，建立单筋矩形截面受弯承载能力本性值或本性模型，必须了解截面极限状态所涉及的词条和词条之间的关系表达式，而词条主要通过单筋梁试验和极限破坏认识分析得到，词条的关系式主要通过力和弯矩的截面平衡关系式来描述。

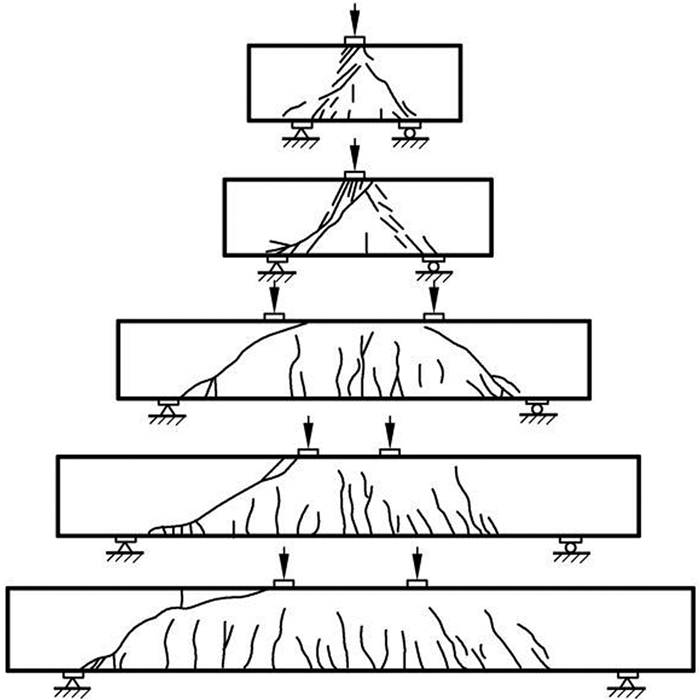
(二)无腹筋梁斜截面受剪承载能力本体模型

由图 3可知，无腹筋梁剪切破坏与梁上荷载的传递路径有关，传递路径主要包括梁机构传递和拱机构传递。剪跨比λ是影响荷载传递路径的主要因素，进而影响无腹筋梁截面的应力状态，因而取λ的影响系数α_c为词条；剪切破坏的特征包含混凝土的拉裂特征，因而一般取混凝土抗拉强度f_t作为词条；纵筋配筋率ρ可以提高无腹筋梁截面的抗剪承载能力，因而取纵筋配筋率的影响系数β_ρ为词条；无腹筋梁的截面形状会影响抗剪承载能力极限状态，因而截面尺寸(截面宽度b和截面有效高度h₀)也作为词条；尺寸效应会影响截面抗剪承载能力，因而尺寸效应影响系数β_h也作为词条。

综上可知，无腹筋梁斜截面受剪承载能力本体模型的词条主要包括α_c、f_t、β_ρ、b、h₀、β_h。

认识到无腹筋梁的受剪机理复杂，影响因素很多，很难综合考虑，至今尚未建立全面合理的分析模型，且受剪破坏都是脆性的，因而结合文献[1]与文献[8]，采用式(3)作为联系各词条的关系表达式。

$V_c=\alpha_c \beta_h \beta_\rho f_t b h_0$

(3)

式(3)即为无腹筋梁抗剪承载能力的本体模型。

结合上述(一)与(二)本体模型的建模过程，对钢筋混凝土构件抗拉承载能力、抗压承载能力、抗弯承载能力、抗剪承载能力及抗扭承载能力等的本体模型进行合理的建模分析。由此可知，本体模型是钢筋混凝土设计原理课程行之有效的学习和教学方法。

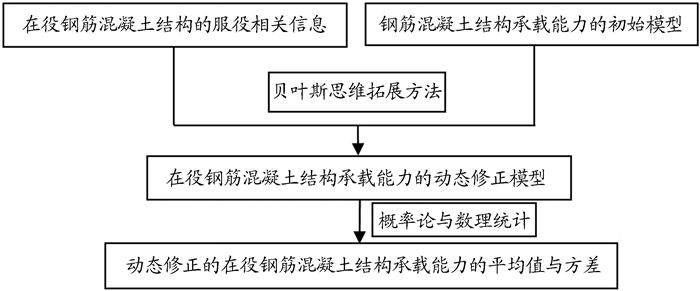
六、钢筋混凝土结构设计原理课程内容的贝叶斯拓展

在进行钢筋混凝土构件安全性极限承载能力和适用性承载能力分析过程中，所得的计算公式均存在大量主观认识(如：许多参数都是主观认识的产物)，因而为了更加客观地掌握和了解承载能力的实际情况，有必要对教材承载能力理论值进行动态修正。主要采用贝叶斯思维方法对钢筋混凝土结构承载能力进行修正。修正思路如图 4所示。(1)结合钢筋混凝土结构安全性/适用性承载能力的理论计算公式(即上述承载能力的本体模型)，考虑到模型中变量的随机性，采用数值模拟方法，得到钢筋混凝土结构初始承载能力的概率分布模型；(2)利用服役钢筋混凝土结构的服役信息，包括退化信息和验证荷载效应信息等，采用贝叶斯思维方法^[9]，即可得到服役钢筋混凝土结构的时变修正模型；(3)结合概率论相关知识，即可得到服役钢筋混凝土结构承载能力动态修正的平均值和方差。结合图 4，实现混凝土抗压强度和钢筋抗拉强度的动态修正分析。

结合图 4，给出钢筋混凝土结构设计原理课程钢筋混凝土梁在服役情况下受弯承载能力的动态修正过程，其他承载能力的动态修正过程(或拓展过程)可参考进行。

钢筋混凝土设计原理课程中适筋梁受弯承载能力分析是很重要的一部分内容，根据文献[1]与文献[8]可以得到适筋梁的初始受弯承载能力R(即上述本体模型值)，考虑到混凝土和钢筋两种材料标准强度以及截面尺寸的随机性，采用蒙特卡罗模拟方法得到考虑随机性的适筋梁受弯承载能力R的概率密度函数和分布函数f_R(x)和F_R(x)。考虑到在役钢筋混凝土梁的相关服役信息，通过贝叶斯思维方法^[9]对f_R(x)和F_R(x)分别进行修正，实现对适筋梁受弯承载能力R的拓展分析。

(一)钢筋混凝土梁的服役信息

在役钢筋混凝土受弯梁的服役相关信息包括受弯承载能力的退化信息如式(4)所示和历史随机性验证荷载效应信息(历史验证弯矩信息)。结合退化信息，得到不同时刻受弯承载能力的相互关系，如式(5)所示。对于服役钢筋混凝土受弯构件，退化信息可以通过查阅相关文献得到；随机性验证荷载效应(或随机性验证弯矩)主要基于监测或检测系统得到的应变信息，通过材料力学中应变与弯矩之间的数学表达式得到

$R(t)=R_0 \cdot g(t)$

(4)

式中：R₀为适筋梁的理论承载力计算值；g(t)为R₀的退化函数，如式(5)所示。

$g(t)=1-k \cdot t^\alpha$

(5)

式中：α为比率参数；k为退化函数的单因子。

基于式(4)，可得第t_i时刻的抗力R(t_i)与当前时刻的抗力R(t_p)的关系式为

$R\left(t_i\right)=\frac{R\left(t_p\right) \cdot g\left(t_i\right)}{g\left(t_p\right)}$

(6)

由于钢筋混凝土梁在服役过程中，会同时受到退化函数和验证荷载效应的影响，因而它的受弯承载能力会不断发生变化，因而有必要让学生了解承载能力的变化规律。后续会采用贝叶斯思维方法对承载能力进行动态修正分析，从而得到服役梁承载能力的变化规律。

(二)服役梁受弯承载能力的贝叶斯修正拓展 1. 考虑验证荷载效应的在役钢筋混凝土梁承载能力贝叶斯修正拓展

假定R与Q^*相互独立，服役梁经历Q^*之后仍然安全，进而可得R>Q^*。利用贝叶斯方法可得修正的承载能力概率分布为

$F_{R . \text { up }}(x)=\frac{P\left[R \square x, R-Q^*>0\right]}{P\left[R-Q^*>0\right]}$

(7)

式中：P[R□x, R－Q^*>0]=$\int\limits_{-\square}^x F_{Q^*}(u) f_R(u) \mathrm{d} u$, P[R－Q^*>0]=$\int\limits_{-\square}^{+\square} f_R(x) F_{Q^*}(x) \mathrm{d} x$。

进一步可得修正的承载能力概率密度函数和概率分布函数分别为

$f_{R, \text { up }}(x)=\frac{F_{Q^*}(x) f_R(x)}{\int\limits_{-\square}^{+\square} f_R(x) F_{Q^*}(x) \mathrm{d} x}$

(8)

$F_{R, \text { up }}(x)=\frac{\int\limits_{-\square}^x F_{Q^*}(u) f_R(u) \mathrm{d} u}{\int\limits_{-\square}^{+\square} f_R(x) F_{Q^*}(x) \mathrm{d} x}$

(9)

考虑到不同服役期内验证荷载效应的分布函数不同，因而可将式(8)与式(9)进一步修正

$f_{R, \text { up }, n}(x)=\frac{f_R(x) \prod\limits_{i=1}^n F_{Q^*, i}(x)}{\int\limits_{-\square}^{+\square} f_R(x) \prod\limits_{i=1}^n F_{Q^*, i}(x) \mathrm{d} x}$

(10)

$F_{R, \text { up }, n}(x)=\frac{\int\limits_{-\square}^x f_R(x) \prod\limits_{i=1}^n F_{Q^*, i}(x) \mathrm{d} u}{\int\limits_{-\square}^{+\square} f_R(x) \prod\limits_{i=1}^n F_{Q^*, i}(x) \mathrm{d} x}$

(11)

式中：F_{Q^*, i}(x)为第i个服役期验证荷载效应所服从的概率分布函数。

2. 考虑退化函数和验证荷载效应的承载能力贝叶斯修正拓展

考虑到退化函数和验证荷载效应历史，结合式(4)、式(6)，式(10)与式(11)可修正为

$f_{R, \text { up }, n, g(t)}(x)=\frac{f_R(x) \prod\limits_{i=1}^n F_{Q^*, i}\left(\frac{x \cdot g\left(t_i\right)}{g\left(t_p\right)}\right)}{\int\limits_{-\square}^{+\square} f_R(x) \prod\limits_{i=1}^n F_{Q^*, i}\left(\frac{x \cdot g\left(t_i\right)}{g\left(t_p\right)}\right) \mathrm{d} x}$

(12)

$F_{R, \text { up }, n, g(t)}(x)=\frac{\int\limits_{-\square}^x f_R(x) \prod\limits_{i=1}^n F_{Q^*, i}\left(\frac{x \cdot g\left(t_i\right)}{g\left(t_p\right)}\right) \mathrm{d} x}{\int\limits_{-\square}^{+\square} f_R(x) \prod\limits_{i=1}^n F_{Q^*, i}\left(\frac{x \cdot g\left(t_i\right)}{g\left(t_p\right)}\right) \mathrm{d} x}$

(13)

了解在役钢筋混凝土梁受弯承载能力的值，主要通过平均值和方差来体现，进一步采用概率论相关理论可得修正承载能力的平均值与方差分别为：

$\mu_{R, \text { up }, n, g(t)}=\left\{\int\limits_{-\square}^{+\square} x f_R(x) \prod\limits_{i=1}^n F_{Q^*, i}\left(\frac{x \cdot g\left(t_i\right)}{g\left(t_p\right)}\right) \mathrm{d} x\right\} /\left\{\int\limits_{-\square}^{+\square} f_R(x) \prod\limits_{i=1}^n F_{Q^*, i}\left(\frac{x \cdot g\left(t_i\right)}{g\left(t_p\right)}\right) \mathrm{d} x\right\}$

(14)

$\sigma_{R, \text { up }, n, g(t)}^2=\frac{\int\limits_{-\square}^{+\square}\left(x-\mu_{R, u p, n, g(t)}\right)^2 f_R(x) \prod\limits_{i=1}^n F_{Q^*, i}\left(\frac{x \cdot g\left(t_i\right)}{g\left(t_p\right)}\right) \mathrm{d} x}{\int\limits_{-\square}^{+\square} f_R(x) \prod\limits_{i=1}^n F_{Q^*, i}\left(\frac{x \cdot g\left(t_i\right)}{g\left(t_p\right)}\right) \mathrm{d} x}$

(15)

结合式(1)~(15)，实现抗力的概率动态修正分析。基于动态修正的抗力分布结果，我们通过以下原则来判断实际的抗力信息：(1) 如果修正之后的抗力标准差小于修正之前的值，则修正之后的抗力客观性较强，更为符合实际情况；(2) 如果修正之后的抗力标准差大于修正之前的值，则修正之后的抗力主观性较强，修正结果较为不可靠。因此，要得到更为实际的修正的抗力信息，就必须得到可靠的构件服役信息或详尽的验证荷载效应信息，一般通过现场无损检测或破坏性试验来获取似然信息。

七、结语

钢筋混凝土梁的抗弯承载能力、抗剪承载能力、抗扭承载能力和钢筋混凝土柱的抗拉承载能力、抗压承载能力均可以通过建立本体模型得到较好的理解和掌握。前提必须通过试验和理论分析(即认识论)得到合适的词条以及词条之间的关系表达式。因此，抓住本体模型的基本理论和对应的建模过程，可轻松建立每一章与之对应的教学思路。