2. 东南大学 经济管理学院, 江苏 南京 211102
2. School of Economics and Management, Southeast University, Nanjing 211102, P. R. China
市场风险是指由资产价格波动导致投资者收益的不确定性。流动性风险源于流动性的不足,是指资产不能按照市场价格立即变现而使变现价格产生的不确定性[1]。投资者尤其是机构投资者变现资产的过程不可避免地将影响资产价格,产生流动性风险。在指令驱动市场中,如A股市场,如果投资者投资理念趋同、持股集中或者发生羊群效应,有可能进一步加大流动性风险[2]。因此,在测度市场风险时,有必要考虑流动性风险因子。20世纪90年代以来,随着VaR技术在风险管理方面的广泛应用,一些学者对传统的VaR方法进行扩展,提出了经流动性调整的VaR模型(Liquidity-adjusted VaR,简称La-VaR)。Bangia等[3]提出了著名的BDSS模型,创造性地在传统VaR的基础上加上可观测的买卖价差作为流动性风险。此后,Le Saout[4],Francois-Heude和Wynendaele[5]使用这种方法进行了研究,胡经生等[6]、陈剑利等[7]也借鉴Bangia等[3]的方法研究中国市场。宋逢明、谭惠[8]建立了一个对流动性风险进行调整的VaR模型,用以度量中国股票的价格风险和流动性风险。胡小平和李超杰[9]、谢福座和左柏云[10]基于Copula方法测度了经流动性调整的市场风险。张金清和李徐[2]、张蕊等[11]基于Copula方法研究了市场风险与流动性风险的集成(整合)风险。
Copula方法是多资产、多风险建模的常用方法,但现阶段测度经流动性调整的市场风险,或者研究市场风险与流动性风险的集成(整合)风险时,主要采用的是常相关Copula模型(静态Copula模型),即Copula函数的参数是常量,而事实上金融时间序列间的相关性会随市场波动而发生变化,这就需要建立新模型来描述时间序列之间的动态(时变,Time-varying)相关结构。最先研究时变Copula模型的是Patton[12],他提出用一个类似ARMA(1, 10) 的过程来描述二元Copula函数的相关参数。Patton[13]随后基于时变Copula研究了汇率间非对称相关性。Mendes[14]基于时变Copula测度了投资组合的CVaR。罗付岩、邓光明[15]基于时变Copula模型估计了投资组合的VaR。周好文、晏富贵[16]基于时变Copula研究了基金、股票和国债动态尾部相关性。
市场处于常态时,流动性充裕,只需付出较小的流动性成本就能完成投资交易,而当市场巨幅下跌,市场风险较大时,投资者可能需要付出巨大的流动性成本才能完成交易,甚至不能进行交易(如金融危机时),也就是说,极端情况下,市场风险与流动性风险的相关性可能呈现出与正常情况下不一样的特征。静态Copula模型无法准确地刻画这一特征,需要借助于时变Copula方法。基于此,本文基于时变Copula方法研究经流动性调整的市场风险:首先基于GARCH-EVT模型对市场风险因子和流动性风险因子建模,然后应用时变Copula测度市场风险因子与流动性风险因子间的动态相关结构,最后应用Monte Carlo方法模拟市场风险因子和流动性风险因子,计算经流动性调整的市场风险La-VaR和La-ES值。
一、市场风险和流动性风险因子市场风险因子一般使用收益率来描述。设Pt为资产的收盘价,将资产损失率定义为:
| $ {R_{\rm{t}}} = - \ln \left( {{P_{\rm{t}}}/{P_{{\rm{t}} - 1}}} \right) $ |
流动性是证券市场的重要属性,学术界一般认为流动性是在不改变价格或价格微小变动的情况下迅速完成大规模交易的能力。一般而言,若单位时间完成单位成交量引起的价格变化越小,则市场流动性越好。流动性风险源于流动性的不足,是指资产不能按照市场价格立即变现而使变现价格产生的不确定性[2]。刻画流动性的指标很多,本文采用谢福座、左柏云[10]的流动性指标来描述流动性风险因子:
| $ {L_{\rm{t}}} = \left( {{P_{\max }} - {P_{\min }}} \right)/{P_{\min }}/{V_{\rm{t}}} $ |
其中,Pmax是日最高价,Pmin是日最低价,Vt为当日成交额。该指标的分子为股价的日波动率,可理解为日价差,这样Lt可以理解为一个交易日内单位成交金额所导致的最大价格变动。Lt的值越小,则流动性越好。
进一步,可以根据该指标计算在一个交易日内变现金额为V0时的变现损失率,即
| $ L{R_{\rm{t}}} = {L_{\rm{t}}}{V_0} $ |
那么,考虑了流动性的资产损失率为
| $ \begin{array}{l} La{R_{\rm{t}}} = {R_{\rm{t}}} + L{R_{\rm{t}}} = - \ln \left( {{P_{\rm{t}}}/{P_{{\rm{t}} - 1}}} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\left[ {\left( {{P_{\max }} - {P_{\min }}} \right)/{P_{\min }}/{V_{\rm{t}}}} \right] * {V_0} \end{array} $ |
金融时间序列的一个显著特点是存在条件异方差,Engle于1982年提出自回归条件异方差(ARCH)模型来刻画时间序列的条件二阶矩性质,并通过条件异方差的变化来刻画波动的时变性及聚集性。用ARCH模型对非平稳时间序列建模过程中会遇到滞后阶数过大甚至趋于无穷,导致计算上的过高复杂性,这就引入了广义ARCH—GARCH(P, Q)模型。
| $ \left\{ \begin{array}{l} {R_{\rm{t}}} = {\mu _{\rm{t}}} + {\varepsilon _{\rm{t}}}\\ {\varepsilon _{\rm{t}}} = {\sigma _{\rm{t}}}{z_{\rm{t}}},{z_{\rm{t}}} \sim i.\;i.\;F\left( \cdot \right)\\ \sigma _{\rm{t}}^2 = w + \sum\limits_{i = 1}^q {{\alpha _i}\varepsilon _{{\rm{t}} - i}^2} + \sum\limits_{i = 1}^p {{\beta _i}\sigma _{{\rm{t}} - i}^2} \end{array} \right. $ | (1) |
其中,p≥0,q≥0,α0≥0, αi≥0(i=1, 2, …, q),βi≥0(i=1, 2, …, p)。
(二) 极值理论(EVT)一般来说,金融资产收益都具有尖峰厚尾的特征,极值理论(EVT)仅针对尾部建模,避开了分布假设难题,有助于处理风险度量中的厚尾问题。基于EVT建模时,必须要求收益率序列独立同分布,因此,本文首先采用GARCH模型对收益率序列建模,提取标准化残差zt。假设F(z)为Z(zt所对应的随机变量)的分布函数,u为阈值,z-u表示超额值,其超额分布函数记为:
| $ \begin{array}{l} {F_u}\left( y \right) = P\left( {Z - u \le y\left| {Z > u} \right.} \right) = \left( {F\left( z \right) - } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\left. {F\left( u \right)} \right)/\left( {1 - F\left( u \right)} \right) \end{array} $ | (2) |
对于条件超额分布函数Fu(y),存在一个广义Pareto分布函数GPDξ, β(y)使得Fu(y)≈GPDξ, β(y),即对于充分大的阈值u,超额值的分布函数可以用广义Pareto分布(GPD)近似。即
| $ {\rm{GP}}{{\rm{D}}_{\xi ,\beta }}\left( y \right) = \left\{ \begin{array}{l} 1 - {\left( {1 + \xi \frac{y}{\beta }} \right)^{ - 1/\xi }}\;\;\;\;\xi \ne 0\\ 1 - \exp \left( { - \frac{y}{\beta }} \right)\;\;\;\;\;\xi = 0 \end{array} \right. $ | (3) |
其中,ξ是形状参数,β是尺度参数。ξ>0表示是厚尾的;当ξ < 0时,0≤x≤-β/ξ。
由于下跌风险普遍受关注,所以本文只考虑下尾阈值。将基于阈值u的zt的分布定义为:
| $ {F_{\xi ,\beta }}\left( z \right) = \left\{ \begin{array}{l} P\left( z \right)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;z < u\\ 1 - \frac{{nu}}{n}{\left( {1 + \xi \frac{{z - u}}{\beta }} \right)^{ - 1/\xi }}\;\;\;\;\;\;\;\;z \ge u \end{array} \right. $ | (4) |
其中,P(z)是经验分布函数(也可以用其他分布来描述,因为极值理论关心的是尾部数据的拟合,所以对中间数据的分布拟合没有任何要求)。
(三) 时变Copula时变Copula与非时变Copula的主要区别在于Copula函数的参数,前者是动态变化的,后者是固定常数。Patton[12-13]提出了时变正态Copula(记作N-Copula)、时变T-Copula、时变rotated Gumbel Copula(记作RG-Copula)和时变Symmetrized Joe-Clayton Copula(记作SJC-Copula)四种函数,其中时变T-Copula函数仅仅假设相关系数是时变的,自由度υ仍然是常量。时变N-Copula、T-Copula的相关系数演化方程分别为
| $ \begin{array}{l} {\rho _{N,{\rm{t}}}} = \Lambda \left( {{\omega _N} + {\beta _N}{\rho _{t - 1}} + } \right.\\ \;\;\;\;\;\;\;\;\;\;\left. {{\alpha _N} \times \frac{1}{{10}}\sum\limits_{j = 1}^{10} {{\mathit{\Phi }^{ - 1}}\left( {{u_{{\rm{t}} - j}}} \right){\mathit{\Phi }^{ - 1}}\left( {{v_{{\rm{t}} - j}}} \right)} } \right) \end{array} $ | (5) |
| $ \begin{array}{l} {\rho _{T,{\rm{t}}}} = \Lambda \left( {{\omega _T} + {\beta _T}{\rho _{{\rm{t}} - 1}} + {\alpha _T} \times \frac{1}{{10}}\sum\limits_{j = 1}^{10} {{T^{ - 1}}\left( {{u_{{\rm{t}} - j}};} \right.} } \right.\\ \;\;\;\;\;\;\;\;\;\left. {\left. \upsilon \right){T^{ - 1}}\left( {{v_{t - j}};\upsilon } \right)} \right) \end{array} $ | (6) |
其中,Λ(x)≡(1-e-x)/(1+e-x)是一种修正的Logistic变换,它的引入是为了确保ρN, t始终落在(-1, 1) 内;Φ-1(·)表示标准正态分布的逆分布;T-1(·;υ)表示自由度为υ的标准T分布的逆分布。
(四) La-VaR计算步骤按照上文的定义及测度模型,经流动性调整的市场风险La-VaR和La-ES计算步骤如下。
步骤1:分别对市场风险因子和流动性风险因子建模。检验市场风险因子和流动性风险因子的自相关性、ARCH效应,如果存在ARCH效应,就基于GARCH-EVT模型建模,否则在消除了自相关性后,直接用EVT建模。
步骤2:选择合适的时变Copula函数类型对市场风险因子和流动性风险因子的联合分布建模,准确地描述两类风险因子间的动态相关结构。
步骤3:基于Monte Carlo模拟法,根据两风险因子间的动态相关结构以及各自的边缘分布,模拟出与原始数据具有相同特征的风险因子时间序列,计算经流动性调整的损失率,计算La-VaR和La-ES。
三、实证分析 (一) 描述性统计分析本文主要研究中国股票市场经流动性调整的市场风险。基于简单但不失一般性的原则,选择沪深300指数代表中国沪、深股票市场。样本考察期为2005年1月4日至2010年12月31日,共1 456组数据。所有数据来源于大智慧软件,数据处理采用S-plus8.0和Matlab7.9。
2005年1月4日至2010年12月31日,共1 456个交易日,其中231个交易日沪深300指数成交额(实际上是沪深300指数中包含的所有股票的总成交额,单位:元)在109~1010之间,1 225个交易日的成交额在1010~1011之间。因此,本文假定日成交额为1010,即V0=1010。
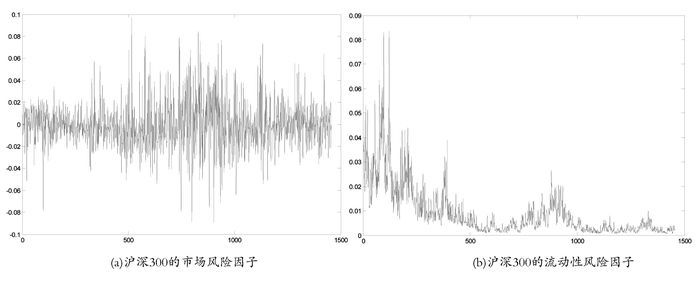
将沪深300指数的市场风险因子和流动性风险因子分别记为Rhsh和Lhsh,其描述性统计如表 1所示。由表 1可知,在样本观察期间内,沪深300指数平均收益均为正(表 1中给出的是负对数收益率)。峰度统计量和J-B检验统计量均表明市场风险因子和流动性风险因子均不服从正态分布。ARCH效应检验表明,滞后10阶,市场风险因子和流动性风险因子都具有明显的条件异方差性。Ljung-Box Q统计量显示,滞后10阶,在5%的显著水平下,市场风险因子和流动性风险因子均具有自相关性。单位根ADF检验表明,所有的序列都是平稳的。总体来看,市场风险因子与流动性风险因子均具有高峰、厚尾、条件异方差性。适合用GARCH模型建模。图 1给出了市场风险因子与流动性风险因子的变化趋势。
| 表 1 市场风险因子和流动性风险因子的描述性统计 |
|
图 1 沪深300指数的市场风险因子和流动性风险因子 |
基于Ljung-Box Q检验,并结合AIC和SC准则,最终选择AR(1) -GARCH(1, 1) -t对Rhsh建模,选择AR(5) -IGARCH(1, 1) -t对Lhsh建模。为节约篇幅,略去均值方程的参数估计结果,仅给出波动方程的参数估计结果,见表 2。
| 表 2 市场风险因子和流动性风险因子的GARCH模型参数估计结果 |
对市场风险因子和流动性风险因子的标准化残差进行Ljung-Box Q检验和ARCH效应检验(表 2的最后两列),发现消除了自相关性和ARCH效应,说明边缘分布建模是合理的,可以应用极值理论对标准化残差的尾部分布建模。
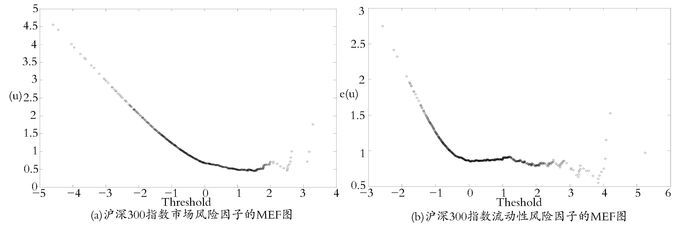
基于EVT建模,关键问题之一是确定阈值u。根据市场风险因子和流动性风险因子的标准化残差序列,作出MEF图(平均超额函数图),如图 2所示。从图 2可以看出,当u在-1左右时,MEF图基本为一条直线,但不能精确到具体的值。采用试验的办法,分别将-0.8到-1.2之间的数作为阈值,采用极大似然函数法进行参数估计,选择最大似然函数值所对应的阈值作为下尾阈值,下尾阈值及下尾分布的参数估计结果见表 3。
|
图 2 市场风险因子和流动性风险因子的经验超额函数图(MEF) |
| 表 3 市场风险因子和流动性风险因子的尾部分布参数估计结果 |
对风险因子的标准化残差序列进行概率积分变换,得到在(0, 1) 上服从均匀分布的时间序列。借助于Matlab7.9估计时变N-Copula和时变T-Copula模型的参数,结果如表 4所示。
| 表 4 时变Copula参数的演化方程估计结果 |
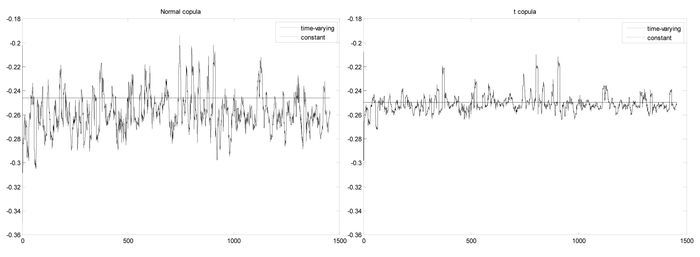
由表 4可知,无论是时变N-Copula还是时变T-Copula,市场风险因子与流动性风险因子的相关系数的滞后项系数为负,表明市场风险因子与流动性风险因子的相关性具有一定的“矫正”能力。图 3给出了基于时变N-Copula和时变T-Copula的相关系数演化趋势,发现,基于时变N-Copula相关系数的波动幅度较之时变T-Copula相关系数的波动幅度大。对时变相关系数进行描述性统计分析(表 5),发现:时变相关系数的峰度要低于正态分布的峰度,J-B统计量也表明相关系数不服从正态分布;滞后10阶,具有ARCH效应;Ljung-Box Q统计量表明相关系数序列具有较强的自相关性(这与表 4得出的结论是一致的)。
| 表 5 基于时变Copula模型的时变相关系数描述性统计 |
|
图 3 市场风险因子与流动性风险因子的动态相关系数 |
为检验时变Copula建模的合理性,并与常相关Copula模型进行比较,对经流动性调整的市场风险值La-VaR进行Kupiec检验,也称LR似然比检验,其基本思想是假定实际考察天数为N0,失败天数为n,则失败率为p=n/ N0。设La-VaR置信度为p*。假定La-VaR估计具有时间独立性,则失败天数n服从参数为N0和p的二项分布,即n~B(N0, p),在零假设p=p*下,似然比LR=-2ln[(1-p*) N0-n(p*)n]+2ln[(1-n/N0) N0-n(n/ N0) n]~χ2(1),在5%的显著水平下,如果LR>3.841 5,拒绝本模型。表 6给出了1%和5%显著水平下的检验结果:失败天数、失败率及LR统计值。
| 表 6 集成风险La-VaR的Kupiec检验结果(1 456个时点,每个时点模拟5 000次) |
由表 6可以看出,无论95%的置信度还是99%的置信度,基于时变Copula模型的La-VaR预测效果均优于常相关模式下的预测效果。T-Copula模型的预测效果要普遍要优于N-Copula,一个可能的解释是T-Copula模型能较好地刻画上、下尾部相关性。但无论是N-Copula,还是T-Copula,99%置信度下的预测效果要优于95%置信度下的预测效果。
进一步,基于时变T-Copula模型,采用Monte Carlo方法可以得到,若投资1单位,当股市日成交额为1010元,即V0=1010时,样本期内,95%置信度下,经流动性调整的市场风险日均La-VaR为0.029 7单位,日均La-ES为0.048 0单位;市场风险日均VaR为0.036 4单位,日均ES为0.055 0单位;流动性风险日均VaR为0.000 3单位,日均ES为0.000 7单位。由此可见,当股市日成交额为1010元时,中国股市主要面临的是市场风险。
四、结论Michael认为,流动性风险可能是继信用风险之后,金融业面临的下一个最重要的风险,而流动性风险的研究远远落后于市场风险和信用风险的研究[17]。现阶段主要采用静态Copula方法测度经流动性调整的市场风险,本文将时变Copula方法引入到风险测度中,提出了基于时变Copula的经流动性调整的市场风险动态测度方法,并基于沪深300指数测度了中国股票市场经流动性调整的市场风险La-VaR和La-ES。Kupiec检验发现,在预测La-VaR时,基于时变Copula模型的效果要优于常相关下的Copula模型,并且,时变T-Copula的预测效果优于N-Copula的预测效果。
| [1] | AMIHUD Y, MENDELSOHN H. Asset pricing and the bid-ask spead[J]. Journal of Financial Economics, 1986, 17: 223–249. DOI: 10.1016/0304-405X(86)90065-6 |
| [2] | 张金清, 李徐. 流动性风险与市场风险的集成度量方法研究[J]. 系统工程学报, 2009, 24(2): 164–172. |
| [3] | BANGIA A, DIEBOLD F X, SCHUERMANN T, STROUGHAIR J D.Modeling liquidity risk, with implications for traditional market risk measurement and management[R].The Wharton Financial Institutions Center, NYU Working Paper, No. FIN-99-062. |
| [4] | Le SAOUT E.Incorporating liquidity risk in VaR models[R].Working paper, University de Rennes, 2001. |
| [5] | FRANÇOIS-HEUDE A, WYNENDAELE V P.Integrating liquidity risk in a parametric intraday VaR framework[C]//7th Bergian Financial Research Forum, Liége, 2002. |
| [6] | 胡经生, 王荣, 丁成. VaR方法及其拓展模型在投资组合风险管理中的应用研究[J]. 数量经济技术经济研究, 2005(5): 141–150. |
| [7] | 陈剑利, 叶东僵, 周明华. VaR在流动性风险测度组合的运用[J]. 浙江工业大学学报, 2009, 37(5): 586–590. |
| [8] | 宋逢明, 谭惠. VaR模型中流动性风险的度量[J]. 数量经济技术经济研究, 2004(6): 114–123. |
| [9] | 胡小平, 李超杰. 基于Copula方法计算La-ES[J]. 西安电子科技大学学报:社会科学版, 2009, 19(4): 59–64. |
| [10] | 谢福座, 左柏云. 基于La-Copula-EVT模型的我国股票市场风险价值研究[J]. 南京财经大学学报, 2010(4): 52–58. |
| [11] | 张蕊, 王春峰, 房振明, 等. 市场风险与流动性风险整合风险度量研究[J]. 北京理工大学学报:社会科学版, 2010, 12(5): 18–22. |
| [12] | PATTON A J.Modeling time-varying exchange rate dependence using the conditional copula[R].Department of Economics, University of California, San Diego, 2001. |
| [13] | PATTON A J. Modeling asymmetric exchange rate dependence[J]. International economic review, 2006, 47(2): 527–556. DOI: 10.1111/iere.2006.47.issue-2 |
| [14] | MENDES B V M. Computing conditional VaR using time-varying copulas[J]. Revista Brasileira de Finanças, 2005, 3(2): 251–265. |
| [15] | 罗付岩, 邓光明. 基于时变Copula的VaR估计[J]. 系统工程, 2007, 25(8): 28–33. |
| [16] | 周好文, 晏富贵. 基于时变Copula的基金、股票和国债动态尾部相关性分析[J]. 西安交通大学学报:社会科学版, 2010, 30(4): 21–26. |
| [17] | MICHAEL. The trading dynamics of close-substitute futures markets:Evidence of margin policy spillover effects[J]. Journal of Multinational Financial Management, 2004, 14(4/5): 463–483. |
 2013, Vol. 19
2013, Vol. 19
