b. 吉林大学 商学院, 吉林 长春 130012
b. School of Business, Jilin University, Changchun 130012, P. R. China
通货膨胀一直是中国宏观经济调控的一个重要的指示变量。大多数学者使用消费者价格指数(CPI)对中国的通货膨胀水平进行衡量。但由于CPI指数中包含的经济方面比较广泛,其中的一些指标由于受到来自经济中的随机冲击的影响(例如食品及能源等),其短期变动幅度及频率比较大,造成CPI通货膨胀对随机冲击的影响也比较敏感。所以使用它来说明中国通货膨胀的趋势及经济走势存在一些质疑。因而有学者提出核心通货膨胀的概念,核心通货膨胀一般指剔除一些价格变动巨大、频繁或者短期性价格波动的商品或服务后的通货膨胀,更能体现中国通货膨胀以及经济的趋势变化特征。所以从核心通货膨胀的视角分析中国货币政策的特征更加切合实际且具有说服力。近年来中国经济较快且平稳发展的同时,中国政府不断强调转变经济发展方式,进行经济结构调整,以此促进经济进一步发展及经济市场的稳定。那么在此时期中国的货币政策是否发生了区制转移,以及不同区制上的经济政策对宏观经济变量是否存在不同的影响效果,也逐渐受到了学术界的关注。
最早说明核心通货膨胀问题的学者是Friedman[1],他认为“通货膨胀归根结底是一种货币现象”,所以核心通货膨胀应该是由货币存量变化所引起的通货膨胀。随后学者们正式提出核心通货膨胀的概念,说法不一但都认为核心通货膨胀应该代表通货膨胀中持久、长期的成分。Eckstein[2]最早提出了核心通货膨胀的概念,他认为核心通货膨胀为生产要素成本的增长趋势。Bryan和Cecchetti[3]认为应该提取出CPI各分量中的一致变动成分来代表核心通货膨胀。而Quah和Vahev[4]则从产出的角度来度量,他们认为通货膨胀中对产出不存在中长期影响的部分,代表了通货膨胀的核心变动趋势。随后也不断有学者对这一概念进行定义,例如Romer[5]、Blinder[6]、Cristadoro[7]等。学者们根据不同定义提出了多种核心通货膨胀的测算方法,目前使用比较广泛的方法包括:剔除法、滤波法、加权中位数法、动态因子指数法(DFI)以及结构向量自回归(SVAR)方法,并且一直在不断改进。很多中国学者使用了这些方法对中国的核心通货膨胀水平进行了测算,包括侯成琪、龚六堂、张维迎[8],简泽[9],汤丹、赵昕东[10]以及张又懿[11]等。本文通过借鉴上述文章,分别使用滤波法、加权中位数法、SVAR方法,对中国的核心通货膨胀水平进行测算,通过对比选择出对经济解释能力最好的一种进行研究。
而对于货币政策区制问题的研究不断成为国内外研究的焦点,主要分为两个方向:(1) 一国的货币政策是否存在区制划分,以及区制的划分情况;(2) 在不同区制下的货币政策以及经济的特征。目前对第二个方向的研究比较广泛,Frank Schorfheide[12],Troy Davig[13]等分别使用了不同形式的MS-DSGE模型分析了不同区制下的货币政策及经济特征。Leeper、Sims、Tao Zha[14]在研究MS-BVAR方法的基础上对美国货币政策区制变化特征进行了说明。中国学者龙如银、郑挺国[15],何启志、范从来[16]等也分别运用了回归模型以及VAR模型等区制转移方法对中国的通货膨胀动态特征进行刻画,证明中国存在明显的高低区制的划分。对于第一个方向的研究,国外学者Sims、Tao zha[17]以及YuFan Huang[18]等均使用比较分析法,利用MS-BVAR模型与BVAR模型的拟合差异来说明经济是否存在区制转移效应。而国内对此问题的研究比较少,对区制转移问题的研究还只局限在MS-VAR、STAR等统计方法,使用贝叶斯方法对货币政策区制转移特征进行研究的寥寥无几。国内的研究大多数都是直接指定区制转移模型,并没有对中国当前的货币政策是否存在区制转移现象加以验证与说明。所以本文使用BVAR及MS-BVAR模型,基于核心通货膨胀的视角首先对中国货币政策的区制转移效应进行验证,随后分析不同区制下货币政策以及经济的特征。
二、模型介绍由于贝叶斯方法相比频率方法充分利用了样本信息以及参数的先验信息,在进行估计时,具有方差或平方误差更小,能得到更加精确的预测结果等优点。所以本文选择使用贝叶斯方法对模型进行估计。下面对模型进行简单的介绍。
(一) BVAR模型本文使用的贝叶斯向量自回归模型(BVAR)参考Sims和Tao Zha[19]的具体形式:
| $ A\left( L \right){y_{\rm{t}}} + C = {\varepsilon _{\rm{t}}},{\varepsilon _{\rm{t}}}\left| {{y_s},s \prec {\rm{t}} \sim N\left( {0,\mathop I\limits_{m \times m} } \right)} \right. $ |
其中,yt是一个m×1的观测向量,A(L)是一个m×m的滞后系数向量,L为滞后算子,C为一个常数向量。并且假设A(0) 是一个非奇异矩阵,所以上述两个方程提供了数据分布的完全描述。估计此模型时使用贝叶斯方法,加入了数据的先验信息,使估计效果更加精确。
(二) MS-BVAR模型本文使用的马尔科夫区制转移贝叶斯向量自回归模型(MS-BVAR)参考Brandt[20]的文章,模型的具体形式为:
| $ {y_{\rm{t}}} = c\left( {{s_{\rm{t}}}} \right) + \sum\limits_{l = 1}^P {{y_{{\rm{t}}-l}}{B_l}\left( {{s_{\rm{t}}}} \right) + \varepsilon \left( {{s_{\rm{t}}}} \right), } t = 1, 2, \ldots, {\rm{T}}\;\;\;{\varepsilon _{\rm{t}}}\left( {{s_{\rm{t}}}} \right) \sim N\left( {0, \mathit{\Sigma } \left( {{s_{\rm{t}}}} \right)} \right) $ |
其中,yt表示m×1的内生变量向量,st表示变量所处的区制,并且有st=i, i=1, 2, ..., h。c(st)、Bl(st)、ε(st)、
当考虑存在h个区制的区制转移模型时,那么所构建的参数以及观测值的转移概率矩阵应该为一个h×h的矩阵。具体形式为:
| $ Q = \left[{\begin{array}{*{20}{c}} {{P_{11}}} &{{P_{12}}} &{{P_{13}}} & \cdots &{{P_{1h-1}}} &{{P_{1h}}}\\ {{P_{21}}} &{{P_{22}}} &{{P_{23}}} & \cdots &{{P_{1h-1}}} &{{P_{1h}}}\\ {} &{} &{} & \cdots &{} &{}\\ {{P_{h{\rm{1}}}}} &{{P_{h2}}} &{{P_{h3}}} & \cdots &{{P_{hh-1}}} &{{P_{hh}}} \end{array}} \right] $ |
其中,pij=p(st=j|st-1=i)。
状态及转移概率通过滤波平滑算法给定。简单描述为:
| $ \Pr \left( {{s_{\rm{t}}} = j, {s_{{\rm{t}}-1}} = i\left| {{W_{{\rm{t}}-1}}} \right.} \right) = \Pr \left( {{s_{\rm{t}}} = j\left| {{s_{{\rm{t}}-1}} = i} \right.} \right)\Pr \left( {{s_{{\rm{t}} - 1}} = i\left| {{W_{{\rm{t}} - 1}}} \right.} \right) $ |
| $ \Pr \left( {{s_{\rm{t}}} = j, {s_{{\rm{t}}-1}} = i\left| {{W_{\rm{t}}}} \right.} \right) = \Pr \left( {{s_{\rm{t}}} = j, {s_{{\rm{t}}-1}} = i\left| {{W_{{\rm{t}}-1}}, {y_{\rm{t}}}} \right.} \right) $ |
| $ \Pr \left( {{s_{\rm{t}}} = j\left| {{W_{\rm{t}}}} \right.} \right) = \sum\limits_{{s_{{\rm{t-1}}}} = 1}^h {\Pr \left( {{s_{\rm{t}}} = j, {s_{{\rm{t}}-1}} = i\left| {{W_{\rm{t}}}} \right.} \right)} $ |
其中,Wt表示一个在时间t的信息集。这些迭代概率计算可以进行从t=1到T的前向滤波计算,也可以进行从t=T到1的后向平滑计算。以上模型则构成了基准的模型估计框架。接下来把此模型应用到具体的经济问题分析当中。
三、核心通货膨胀率的测算 (一) 数据的选取对于核心通货膨胀率的测算本文选择了具有代表性的3种方法,分别为HP滤波法、加权中位数法以及SVAR方法,它们分别是滤波法、统计法以及模型法的代表。本文根据这3种方法的需要选择了相应的数据序列。使用2001年5月至2013年2月的142个月度数据进行估计。选用月度数据是考虑到其更能体现数据随时间变化的特征,并且月度数据由国家统计局公布,比较容易获得且准确。数据序列包括消费者价格指数(CPI)以及CPI指标核算中包含的8大类及14小类变量数据。其中通货膨胀率数据由CPI同比增长率数据计算得到,计算方法为通货膨胀率=CPI-100。由于产出增长率数据不存在月度数据只存在季度值,所以本文选择工业增加值同比增长率代表月度产出增长率,其中中国的工业增加值同比增长率在每年的1月份存在缺失值,本文采用插值方法补齐。代表货币政策的变量选择的是银行间拆借利率。以上数据的来源为国家统计局网站以及东方财富网、凤凰网、恒生聚源。
(二) 核心通货膨胀的估计对于本文所使用的3种估计方法(HP滤波法、加权中位数法以及SVAR方法)在此不作具体介绍,具体可参考范跃进、冯维江[21]以及陈磊[22]的相关做法。下面给出3种方法的估计结果(图 1)。
|
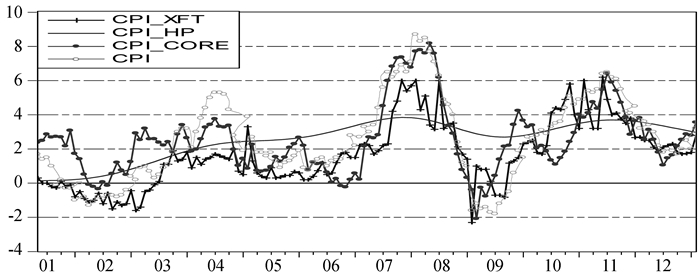
图 1 核心通货膨胀与CPI通货膨胀对比图 |
图 1中CPI代表由CPI同比增长率计算得到的通货膨胀率水平,CPI_HP代表由HP滤波法估计得到的核心通货膨胀率水平,CPI_XFT代表由加权中位数法计算得到的核心通货膨胀率,CPI_CORE代表由SVAR方法计算得到的核心通货膨胀率。对比结果可以看出,3种方法所求解出的核心通货膨胀率均比CPI通货膨胀平滑,波动幅度小。而本文将根据各种判断方法选择一种最具代表性的结果来说明中国的通货膨胀的核心趋势特征。
目前判断核心通货膨胀好坏的方法主要根据Bryan和Cecchetti[3]、Wynne[23]提出的理论,核心通货膨胀应具备的特点包括:(1) 其相对于观测到的通货膨胀更加平滑;(2) 利于预测可以观测的通货膨胀;(3) 度量应该建立在经济理论之上。张又懿[11]认为核心通货膨胀应该从以下几方面来衡量:前瞻性、时效性、易于理解性、理论性以及稳定性。本文沿用Bryan和Cecchetti[3]的判断理论进行检验,所得结果如下。
1. 波动幅度比较根据表 1,从均值角度分析,只有加权中位数方法的核心通货膨胀均值小于CPI通货膨胀,其余两种方法的均值均略大于CPI通货膨胀均值;而从波幅和标准差的角度看,三种方法的结果均小于CPI通货膨胀,而稳定性最好的为HP滤波方法求得的核心通货膨胀,波动较大的为SVAR方法所得结果。
| 表 1 波动幅度对比表 |
本文从相关性的角度来判断核心通货膨胀对CPI通货膨胀的预测能力。从相关性角度看,加权中位数方法所求结果与CPI的相关性较高。HP滤波法的相关性较小(表 2)。
| 表 2 相关性对比表 |
从经济理论的角度考虑,作为货币政策的目标,既要能反映经济的运行情况,又不能过度波动。HP滤波法虽然稳定,波动较小,但其并没有考虑经济变量之间的关系以及经济的现实情况。而SVAR方法与加权中位数法都是从经济的现实情况出发对核心通货膨胀进行的重新估计。相比较来说,加权中位数法具有较小的波动而且对通货膨胀的预测能力更强。
综合考虑以上3个检验指标所得结果,本文选择加权中位数法所得的核心通货膨胀率数据对货币政策与经济的区制效应进行进一步研究。
四、货币政策的区制转移效应本部分研究的重点在于证明中国的货币政策以及经济是否存在明显的区制转移特征,以及使用区制模型来刻画经济是否合理。鉴于在当前的文献中学者大多直接指定某个区制转移模型来刻画经济现实,而没有使用定量的论据来说明此问题,所以本部分通过对比BVAR模型与MS-BVAR模型的拟合及预测效果来加以说明。
下面给出2001年5月到2013年2月中国核心通货膨胀率、利率以及产出增长率的时间路径。横轴为时间轴,纵轴为变量(图 2)。
|
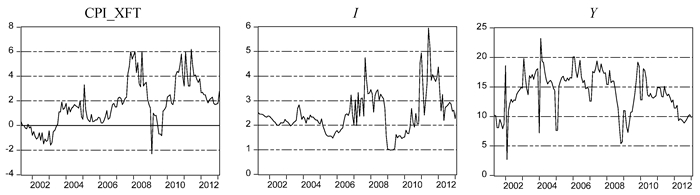
图 2 核心通货膨胀、利率以及产出增长率的时间序列图 |
从图 2中可以直观地看出3个变量在这个时间段内均发生了较大幅度的上下波动,存在着明显的高低区制的划分,但这只是从直观的角度分析,中国的经济及货币政策是否发生了区制转移,还需要通过模型给出具体说明。
在建立VAR模型之前我们对变量的平稳以及相关情况进行检验。首先使用ADF单位根检验方法,判断各变量的平稳情况以及单整阶数。从单位根检验的结果表(表 3)可知3个变量在1%的显著性水平下均是1阶单整过程,有相同的单整阶数,进而可以进行下面的协整检验。
| 表 3 单位根检验 |
根据图 2可知,3个变量均存在截距但不存在明显的变化趋势,所以我们选择有截距但无趋势的协整检验。检验结果(表 4)表明3个变量之间存在不止一个协整关系,也就是存在着共同运动的趋势,所以我们可以对上述变量建立MS-BVAR模型以及BVAR模型。
| 表 4 协整检验 |
根据VAR建模的滞后阶数判断准则AIC、HQ可知,三变量所建模型的滞后阶数为3阶。接下来通过分别建立BVAR模型与MS-BVAR模型,对比模型的样本外预测精确度,以比较两个模型对数据的解释能力,进而判断中国的货币政策是否存在区制转移效应,以及是否应该使用区制转移模型对中国的数据进行描述。首先使用2001年5月至2012年8月的数据分别建立BVAR及MSBVAR模型,本文假设经济包含两个明显的区制特征,所以区制模型包含2个明显区制。继而通过给出两种方法对2012年9月到2013年2月的数据进行样本外预测值,并对比预测值与实际值来判断模型的好坏。本文对于模型的先验设定形式如表 5。
| 表 5 超参数校准表 |
模型的2001年5月到2013年2月的模拟及预测值与实际值的对比结果见表 6。
| 表 6 精度对比图 |
表 6从4个统计量的角度对比了MSBVAR与BVAR模型的短期预测效果,分别为均值、标准差、偏度、峰度,本文将短期假设为6期。从均值和标准差的角度来看,对于利率和产出增长率,MSBVAR模型的预测值都与实际值比较接近,只有核心通货膨胀率水平,BVAR优于MSBVAR。而从数据的偏度及峰度的角度即数据的分布情况看,MSBVAR模型的统计量在3个变量上都与实际值比较接近,而BVAR模型则发生了相对较大的偏离,从这个角度说,MSBVAR模型可以更好地刻画数据的分布特征也即变动特征。综上所述,从短期预测以及数据分布特征的角度来分析,MSBVAR模型更加适合用于分析中国的经济特征。
五、区制转移效应下的经济特征本部分使用全样本即2001年5月到2013年2月的数据建立两区制MS-BVAR模型,对经济以及货币政策进行区制划分,给出区制转移特征以及经济在不同区制之间的特点。首先使用Gibbs sampler方法进行随机摄动抽样,然后使用这个初始的后验样本来识别后验的区制,继而根据此区制划分特点抽取更大的样本来说明经济的特征。本文的总抽样个数为2 500次,去除前500次样本。
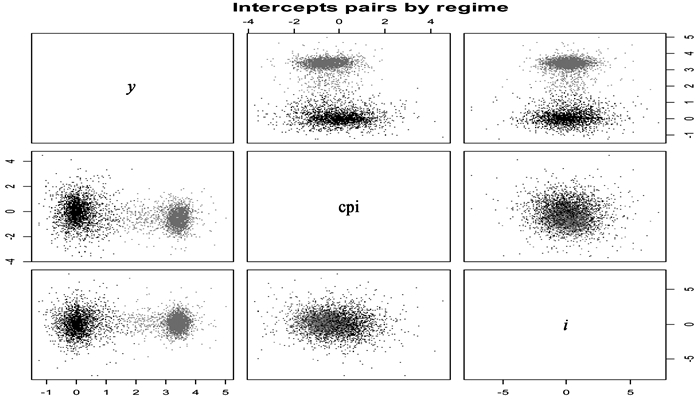
图 3显示的是3个截距项在两个区制之间的配对散点图。根据其所属不同区制给定的不同颜色深度,我们可以从图中清晰看出按3变量分区制的明显程度排序为产出增长率、核心通货膨胀率、利率。本文是从核心通货膨胀的角度观测经济的变化特征,所以接下来本文按照核心通货膨胀的区制分类建立MS-BVAR模型,并观测经济以及货币政策的变化特征。按照核心通货膨胀的角度经济分为两个区制,假设高通货膨胀区制为区制1,低通货膨胀区制为区制2。
|
图 3 截距项配对散点图 |
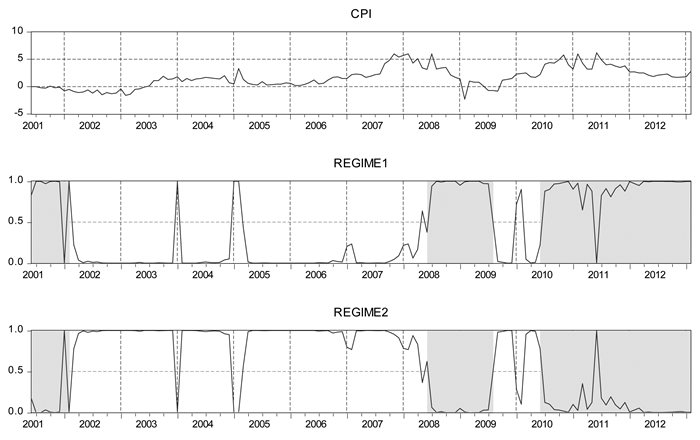
按照核心通货膨胀截距分区制重新进行后验抽样得出区制转移概率图。从图 4可以明确看出有3个时间段明显出现了通货膨胀高涨的现象。高通货膨胀时期主要分布在2001年5月到2002年4月,2008年6月到2009年8月以及2010年6月到2013年2月,其余时间均处于低通货膨胀经济平稳运行阶段。这与现实情况相符。在2008年初期,国际大宗商品价格持续上涨加大了中国的进口压力,并且国内各种食品价格轮番上涨也推动了中国通货膨胀的上升。在此期间货币投放过快以及居民形成的通货膨胀预期都形成了通胀上升的压力。2007年,政府当局频繁使用利率、存款准备金率、公开市场操作等工具进行紧缩性货币政策操作,但全年CPI仍达到104.8,上升势头持续到2008年,峰值达到108.7。由于在2008年发生了全球金融危机,中国的价格水平波动却较小。在2009年下半年价格水平发生一段时间的下降,但是为了应对2008年出现的全球金融危机对中国造成的负面影响,促进经济回升,2008年9月起货币政策操作开始转向适度宽松,到年末4次下调存贷款利率,3次下调存款准备金率,并对大型金融机构和中小金融机构实行了差别化的准备金要求,进一步放松中小金融机构的可贷资金约束。2009年正式转为实施适度宽松的货币政策,主要操作包括维持较低利率水平,配合积极的财政政策,为4万亿经济刺激计划提供信贷资金支持。而在这段时期的刺激及宽松的政策执行后,中国的通胀在2010年下半年出现反弹,2011年通货膨胀明显处于高涨状态,很不利于经济的稳定运行。而后政策转为稳健,但同时采取了适度紧缩的措施,由于货币政策存在滞后性,通胀在2012年末才出现小幅下降。
|
图 4 区制转移图 |
对于不同区制的货币政策效果分析,本文使用下面的转移概率加以说明。由表 7可知,区制1的持续概率为0.985,区制2的持续概率为0.983,所以从核心通货膨胀的视角看,其在两个区制都有较长的持续性。在高通货膨胀的持续时间相对较长。根据持续时间计算公式
| 表 7 区制转移概率 |
本文通过建立贝叶斯向量自回归模型(BVAR)和马尔科夫区制转移贝叶斯向量自回归模型(MS-BVAR模型),从核心通货膨胀的视角研究了中国经济是否存在区制转移效应以及不同通货膨胀区制下的货币政策特征,得出了以下的结论。
其一,核心通货膨胀相对于由CPI计算得出的通货膨胀更加平滑,更能反映经济的趋势变化特征。综合考虑HP滤波法、加权中位数法以及SVAR方法所估计的结果,加权中位数法能更好地体现经济的区制变化特征。
其二,通过BVAR模型与MS-BVAR模型的样本外预测精度的比较发现,MS-BVAR模型的短期预测以及数据的分布特征都更接近实际数据,所以由此判断MS-BVAR模型更适合用来说明中国的经济特征。中国的经济变化存在着明显的区制特征。
其三,不同区制下核心通货膨胀持续性均较大,都达到了0.9以上的持续概率。高通货膨胀区制的平均持续期大致为66个月,而低通货膨胀区制的平均持续期大致为59个月。持续时间较长,说明核心通货膨胀更能代表经济的趋势变化特征,受经济的短期波动成分影响较小。由此给出建议:中国货币当局在治理通货膨胀时,不仅应考虑通货膨胀的短期高低的变化特征,更要注重考虑其长期趋势的变化形式,以及不同区制下的通货膨胀变化特点,这更加有利于经济的平稳发展。
| [1] | FREIDMAN M. Inflation, causes and consequences[M]. New York: Asia Publishing House, 1963. |
| [2] | ECKSTEIN O. Core inflation[M]. Englewood Cliffls, N.J: Prentice-Hall, . |
| [3] | BRYAN M, CECCHETTI S G. Measuring core inflation[M]. MANKIW N G.Monetary policy.Chicago: University of Chicago Press, . |
| [4] | QUAH D, VAHEY S P. Measuring core inflation[J]. The Economic Journal, 1995, 105: 1130–1144. DOI: 10.2307/2235408 |
| [5] | ROMER D. Advanced macroeconomics[M]. New York: McGraw-Hill Companies, 1996. |
| [6] | BLINDER A S.Comment on measuring short-run inflation for central bankers[R].Review, Federal Reserve Bank of st.Louis, 1997. |
| [7] | CRISTADORO R, FORNI M, REICHLIN L. A Core inflation indicator for the Euro area[J]. Journal of Money, Credit and Banking, 2005, 37: 539–560. DOI: 10.1353/mcb.2005.0028 |
| [8] | 侯成琪, 龚六堂, 张维迎. 核心通货膨胀:理论模型与经验分析[J]. 经济研究, 2011(2): 4–18. |
| [9] | 简泽. 中国核心通货膨胀的估计[J]. 数量经济技术经济研究, 2005, 22(11): 3–13. DOI: 10.3969/j.issn.1000-3894.2005.11.001 |
| [10] | 汤丹, 赵昕东. 核心通货膨胀的度量方法及其应用[J]. 宏观经济研究, 2011(7): 28–34. |
| [11] | 张又懿. 核心通货膨胀衡量方法的比较[J]. 中国外资, . DOI: 10.3969/j.issn.1004-8146.2014.01.002 |
| [12] | SCHORFHEIDE F. Learning and monetary policy shifts[J]. Review of Economic Dynamics, 2005(8): 392–419. |
| [13] | DAVIG T, DOH T.Monetary policy regime shifts and inflation persistence[R].Research working papers, 2009. |
| [14] | LEEPER EM, SIMS CA, TAO Z. What does monetary policy do?[J]. Economic Studies Program, 1996, 27: 1–78. |
| [15] | 龙如银, 郑挺国, 云航. Markov区制转移模型与我国通货膨胀波动路径的动态特征[J]. 数量经济技术经济研究, 2005, 22(10): 111–117. DOI: 10.3969/j.issn.1000-3894.2005.10.012 |
| [16] | 何启志, 范从来. 中国通货膨胀的动态特征研究[J]. 经济研究, 2011(7): 91–101. |
| [17] | SIMS CA, TAO Z. Were there regime switches in U.S. monetary policy?[J]. American Economic Review, 2006, 96: 54–81. DOI: 10.1257/000282806776157678 |
| [18] | HUANG Y F.Time-varying policy targets and regime switches in U.S. monetary policy[R].Job Market Paper, 2012. |
| [19] | SIMS CA, TAO Z. Bayesian methods for dynamic multivariate models[J]. International Economic Review, 1998, 39: 949–968. DOI: 10.2307/2527347 |
| [20] | BRANDT P T.Empirical, regime-specific models of international, inter-group conflict, and politics[R]. Working paper, 2009. |
| [21] | 范跃进, 冯维江. 核心通货膨胀测量及宏观调控的有效性:对中国1995-2004的实证分析[J]. 管理世界, 2005(5): 6–13. |
| [22] | 陈磊, 张同斌. 我国通胀率与核心通胀率动态机制实证研究[J]. 数量经济技术经济研究, 2012(12): 97–111. |
| [23] | WYNNE A.Core inflation:A review of some conceptual issues[R].Federal Reserve Bank of Dallas, Research Department Working Paper, 1999(3). |
 2014, Vol. 20
2014, Vol. 20
