2. 东北财经大学 工商管理学院, 辽宁 大连 116025;
3. 重庆师范大学 经济与管理学院, 重庆 401331
2. School of Business Administration, Dongbei University of Finance and Economics, Dalian 116025, P. R. China;
3. School of Economics and Management, Chongqing Normal University, Chongqing 401331, P. R. China
城镇化又称城市化,是指随着生产力的发展和经济社会的进步,人口、资本和土地等要素禀赋及经济社会活动不断向城镇聚集,引致城镇生产和生活空间逐步扩大并随之引起的一系列经济社会变化过程,其表征为人口结构、经济结构、社会结构和空间结构的历史变迁。中国政府于2012年明确提出“新型城镇化”的发展战略并将其确立为未来中国经济发展新的增长动力和扩大内需的重要手段。此后,中国政府又于2014年进一步强调了以促进人的城镇化为核心、提高质量为导向的新型城镇化战略,并将其视为建设现代化国家的关键举措以及实施乡村振兴战略和区域协调发展战略的有力支撑。与此同时,中国制造业依靠在劳动力和资源禀赋上的比较优势取得了飞速发展,奠定了世界第一制造大国的地位。制造业推动了中国国民经济的发展,而“以人为本”的新型城镇化是社会发展与环境协调的基石。毫无疑问,新型城镇化的良性可持续发展及活力主要取决于合理制度条件下的产业生长。没有产业尤其是制造业的支撑,城镇化将变成无本之木、无源之水。那么,中国制造业的发展及其呈现的集聚态势是否显著促进了城镇化的发展?其效应究竟如何?对以上问题的回应无疑具有重要的现实意义和政策蕴含。
一、文献回顾历史经验已经证实,制造业集聚与城镇化在一国或地区经济社会发展中发挥着重要作用,其内在关联成为各国学者关注的热点话题之一。Button基于成本效益的视角,剖析了集聚经济的基本表征和内在本质,研究发现了制造业集聚与城镇化存在互动共生关系[1]。Baldwin研究发现,企业集聚引致的相关制造业集聚以及伴生的人口向城镇产业集中,促进了城镇空间拓展、城镇规模的增长以及城市群的兴起[2]。仇保兴通过分析产业集聚、工业化与城市之间关系,认为制造业集聚是实现城镇化与新型工业化良性互动的重要途径[3]。苏雪串在深入分析制造业集聚推动城镇化进程的内在机制基础上,认为制造业集聚在城镇化中期的加速阶段的作用更为显著[4]。胡伶俐、施祖麟揭示了制造业集聚促进城镇化的内在机制:制造业集聚促进了区域环境的改善,从而推动城镇人口流入,促进产业分工和市场形成,进而为城镇化的形成提供了内在基础[5]。王亚飞等通过构建动态面板协整模型和面板误差修正模型,研究发现了制造业集聚对新型城镇化具有推动作用,而新型城镇化却不是制造业集聚的动力[6]。吴丰林等基于城市数据,探析了制造业集聚的形成机理,研究认为制造业集聚有助于促进优化城市的空间密度和功能形态[7]。李华从空间集聚的视角推演了城镇形成与发展的两阶段模型,认为多样化偏好是制造业集聚的内生动力,而集聚外部性则是制造业集聚促进城镇化发展的内在途径[8]。Mills和Hamilton构建了Mills-Hamilton城市模型,认为镇城化进程的核心动力在于产业的区位选择和集聚过程[9]。罗薇薇以中国广东为例,通过格兰杰因果关系检验发现制造业集聚与城镇化存在互为因果关系[10]。袁丹和雷宏振通过构建空间计量模型研究发现,制造业集聚不仅有助于推动本地城镇化的发展,还促进了相邻地区的城镇化进程[11]。杨仁发和李娜娜的研究表明,制造业集聚能够显著地促进城镇化发展,而服务业集聚则不是城镇化发展的动力[12]。
过往的文献为研究产业集聚与新型城镇化的关系提供了丰富的经验证据和理论基础,但也存在着不足:(1)单一的人口城镇化率作为指标无法全面描述城镇化水平;(2)对于制造业集聚与城镇化的研究大多局限于传统计量方法,缺乏以空间的视角考察二者之间的影响和关系,也未测算出制造业集聚对新型城镇化所产生的空间溢出效应。本文主要贡献在于:(1)依据中国31个省份2003—2015年新型城镇化建设的24个指标,构建了评价城镇化水平的综合指标体系,并基于熵权法对中国省际新型城镇化水平进行测度;(2)研究了制造业集聚与新型城镇化之间的关系,并在省级层面上采用空间计量的方法研究制造业集聚对新型城镇化所产生的空间溢出效应。
二、理论分析与研究假设非农产业向城镇的聚集和农业劳动力向非农劳动力的转移是城镇化渐进演变的本质。经济上具有相互关联的企业由于在地理位置上的邻近从而实现了在运输成本上的节约。集聚经济的存在使得聚集区域内的企业可以通过共享中间产品投入、劳动力储备与匹配以及技术、知识溢出效应提高劳动生产率,从而提高利润与工资水平,引致劳动力不断涌入,同时制造业企业的区位选择在利润最大化原则下也不断向集聚区聚集。在以规模报酬递增和不完全竞争为假设前提的制造业部门中,劳动力集中的地方由于垄断竞争的特性,存在较高的要素报酬,这更加有利于吸引劳动力的进一步汇集,使之成为城镇发展的基础。在工业化初期,工业部门的快速扩张对劳动力具有巨大需求,在劳动力要素存在自由流动以及理性人假设前提下,劳动力将会从收益相对较低的农业部门转移至收益相对较高的工业部门,引致农村人口转移至城镇。由人口集聚形成的规模效应促进了各种成本的有效降低,这加快了各种要素资源向城镇聚集,从而促进城镇化的发展。
人口集聚是城镇规模形成的基础,而产业发展则为城镇经济发展提供了内在支撑。配第—克拉克定律指出,经济发展和收入水平的提高引致产业结构向第三产业的转移,而当前中国正处于这种趋势[12]。制造业集聚促进了生产性服务业的发展,使得集聚区基础设施和公共服务配套更加完善,从而促进金融、研发等现代服务行业投入的扩大。城镇功能的进一步强化则吸引了更高质量的制造业企业进入。制造业与服务业的这种互动发展,促进了产业结构调整和升级,从而有利于能源结构改善,通过整合生产要素推动城镇经济发展从“要素驱动”向“创新驱动”转变以及从“粗放型”的经济发展模型向“集约型”转变,从而改善生态环境、提升居民生活福利,城镇化质量进一步得到提高。据此,本文提出:
假设1:制造业集聚对当地新型城镇化发展具有推动作用。
地理学第一定律指出,任何地理事物或现象之间均存在相关性,地理距离位置更加邻近的事物彼此之间的相关性更高。由于邻近区域之间的经济条件相似、社会文化状况趋同,以人口转移、产业发展、资源聚集、要素流动实现的经济辐射引致邻近区域的空间集聚态势明显[13]。区域经济的发展受到空间因素的影响,空间溢出效应是中国区域经济发展不可忽视的重要部分[14]。
Krugman认为,溢出效应不会因为地理因素而仅仅停留在最初溢出地[15]。在制造业集聚过程中,可能不仅仅会对本地的新型城镇化进程产生影响,还会溢出到其他地区,对周边地区的新型城镇化进程产生影响。一方面,假定生产要素能够在区域之间自由流动,在成本驱动下,制造业集聚不仅会带动本地区农村剩余劳动力和其他生产要素的转移,同时还将带动周边地区同质非农劳动力和其他生产要素的转移。随着集聚程度的提高,资源和要素成本的上升促使本地的制造业向周边地区进行转移,从而形成区域产业协同和联动发展的局面。在制造业集聚所产生的扩散效应的影响下,拥有相似产业结构的城镇之间便具有了联系,以此形成大规模城市。另一方面,基于技术溢出的内生增长具有规模报酬递增的现象,若一个地区比它相邻的地区具有更强的优势,优势越强的地区的经济活动向外扩散的能力也就越强,转移速度也就越快,这就能够为周边地区的发展提供要素和资源,从而为周边地区的发展形成新的增长点[16]。如此一来,本地的制造业集聚过程也将有可能对周边地区的城镇化进程产生影响。据此,本文提出:
假设2:新型城镇化发展具有空间集聚态势。
假设3:制造业集聚对周边地区新型城镇化发展具有空间溢出效应。
三、计量模型、变量选取与数据说明 (一) 计量模型现有研究表明,中国的城镇化在地理空间上存在明显的相关性[17-19]。在产业转移和要素流动等因素的作用下,集聚经济的影响在空间上具有传播和扩散的可能,因而某一地区i的制造业也会对另一地区j的城镇化进程产生影响。若对城镇化和制造业集聚所具有的这种空间关联忽略必然导致在模型的估计上存在偏误以及进行错误的参数检验[20],传统回归分析方法也不适用于解释空间异质性[21]。空间计量模型由于考虑了变量的影响存在空间转移扩散的情况,因此本文通过构建空间计量模型来捕捉制造业集聚和新型城镇化在空间维度上所具有的关联效应,模型构建如下:
| $ \begin{array}{*{35}{l}} \ln \text{n}{{\text{u}}_{i\text{t}}}=\rho W\ln \text{n}{{\text{u}}_{i\text{t}}}+{{\delta }_{1}}{{\operatorname{lnagg}}_{i\text{t}}}+{{\delta }_{2}}{{X}_{i\text{t}}}+{{\theta }_{1}}W\ln {{\operatorname{agg}}_{i\text{t}}}+{{\theta }_{2}}W{{X}_{i\text{t}}}+{{u}_{i}}+{{\gamma }_{\text{t}}}+{{\varepsilon }_{i\text{t}}} \\ {{\varepsilon }_{i\text{t}}}=\lambda W{{\varepsilon }_{i\text{t}}}+{{\mu }_{i\text{t}}} \\ \end{array} $ | (1) |
其中,W是空间权重矩阵,反映各单元之间的空间关系,X为控制变量集合。u代表地区固定效应,γ代表时间固定效应;ε是随机扰动项;ρ和θ为空间滞后系数,反映变量之间的空间依赖关系。λ为空间误差系数,反映随机扰动项中存在的空间关系。若ρ和θ同时为零时,式(1)为空间误差模型(Spatial Error Model,SEM);若λ和θ同时为零时,式(1)为空间滞后模型(Spatial Lagged Model, SLM);若λ为零时,式(1)则为空间杜宾模型(Spatial Dubin Model, SDM),具体的模型设定需待进一步检验。对于式(1),通常采用极大似然方法对其进行参数估计[22]。
对于式(1)中的空间权重矩阵,考虑到0-1邻接权重矩阵无法反映地理上相互邻近但并非相连的个体间的空间影响以及个体间经济上的相互关联性,地理距离权重矩阵和经济距离权重矩阵尽管分别从地理空间和经济行为模式上反映了个体间的联系程度,但实际地区间的空间关联可能并非仅仅来自地理或经济的某一方面[23]。对此,本文参考侯新烁等[24]的方法,借鉴引力模型的思想,将空间权重矩阵定义为:
| $ w_{i, j}=\left\{\begin{array}{ll}{\overline{Q}_{i} \times \overline{Q}_{j} / d_{i j}^{2}} & {i \neq j} \\ {0} & {i=j}\end{array}\right. $ | (2) |
其中,
此外,本文通过Moran’s I及其散点图对中国新型城镇化进行全局空间自相关检验,其描述了研究范围内所有单元之间的整体空间关系。Moran’s I反映了观测值与空间滞后项的相关关系[25],即一个地区上的某一属性值与邻近地区上同一属性值是相关的。Moran’s I定义为:
| $ I=\frac{n}{\sum\limits_{i=1}^{n}{\sum\limits_{j=1}^{n}{{{w}_{ij}}}}}\cdot \frac{\sum\limits_{i=1}^{n}{\sum\limits_{j=1}^{n}{{{w}_{ij}}}}\left( {{x}_{i}}-\bar{x} \right)\left( {{x}_{j}}-\bar{x} \right)}{\sum\limits_{i=1}^{n}{{{\left( {{x}_{i}}-\bar{x} \right)}^{2}}}} $ | (3) |
对于Moran’s I,有Moran’s I
Lesage和Pace指出,通过采用空间计量模型回归结果的点估计系数来判断是否存在空间溢出效应的做法可能得出错误的结论,而对空间回归模型中的变量进行偏微分解释却能作为判定是否存在空间溢出效应的有效手段[26]。对此,把式(1)对应的广义空间计量模型改写为如下形式:
| $ Y=(1-\rho W)^{-1}(X \beta+W X \theta)+R $ | (4) |
其中,R包括了截距项和误差项,对于解释变量X,其对应的Y的期望值的偏导数矩阵可以写为:
| $ \left[ \frac{\partial E(Y)}{\partial {{x}_{1k}}}\cdots \frac{\partial E(Y)}{\partial {{x}_{Nk}}} \right]=\left[ \begin{matrix} \frac{\partial E\left( {{y}_{1}} \right)}{\partial {{x}_{1k}}} & \cdots & \frac{\partial E\left( {{y}_{1}} \right)}{\partial {{x}_{Nk}}} \\ \vdots & \ddots & \vdots \\ \frac{\partial E\left( {{y}_{N}} \right)}{\partial {{x}_{1k}}} & \cdots & \frac{\partial E\left( {{y}_{N}} \right)}{\partial {{x}_{Nk}}} \\ \end{matrix} \right]={{(I-\rho W)}^{-1}}\left[ \begin{matrix} {{\beta }_{k}} & {{w}_{12}}{{\theta }_{k}} & \cdots & {{w}_{1N}}{{\theta }_{k}} \\ {{w}_{21}}{{\theta }_{k}} & {{\beta }_{k}} & \cdots & {{w}_{2N}}{{\theta }_{k}} \\ \vdots & \cdots & \ddots & \vdots \\ {{w}_{N1}}{{\theta }_{k}} & {{w}_{N2}}{{\theta }_{k}} & \cdots & {{\beta }_{k}} \\ \end{matrix} \right] $ | (5) |
其中,直接效应是式(5)中偏导数矩阵的主对角线元素,表示了本地区解释变量对被解释变量的影响;间接效应是式(5)中偏导数矩阵的非对角线元素之和的均值,表示了相邻地区解释变量对本地区被解释变量的影响;而偏导数矩阵本身为总效应,其值为直接效应与间接效应的加总。
(二) 变量界定1.被解释变量:新型城镇化
依据2014—2020年《国家新型城镇化规划》,并参考王亚飞等[6]对新型城镇化指标体系的构建,本文构建了包括经济发展、人口集聚、城乡统筹、基础设施、公共服务、生态环境与科学教育等7个维度24个指标的新型城镇化发展水平评价指标体系,如表 1所示。
| 表 1 新型城镇化发展水平评价指标体系 |
对评价指标体系中指标权重的确定方法通常包括专家评分法、层次分析法、主成分分析法、因子分析法、熵权法等。相比于其他方法,熵权法通过各指标信息熵值的效用确定指标权重,从而有效避免了人为因素的干扰。对此,本文采用熵权法对中国省际新型城镇化水平进行测度。
由于本文所构建的新型城镇化评价体系中各指标在数量级、量纲,以及指标的正负取向上均有所差异,对此需要对数据进行标准化处理。采用式(6)对正向指标进行标准化处理,其值越大表明其对系统的贡献越大;采用式(7)对负向指标进行标准化处理,其值越小对系统贡献越大。
| $ x_{i j}=\frac{a_{i j}-\min \left\{a_{i j}\right\}}{\max \left\{a_{i j}\right\}-\min \left\{a_{i j}\right\}}(i=1, 2, \cdots, m ; j=1, 2, \cdots, n) $ | (6) |
| $ x_{i j}=\frac{\max \left\{a_{i j}\right\}-a_{i j}}{\max \left\{a_{i j}\right\}-\min \left\{a_{i j}\right\}}(i=1, 2, \cdots, m ; j=1, 2, \cdots, n) $ | (7) |
在此基础上,采用熵权法测度中国省际新型城镇化水平步骤如下。
计算第i项指标值在第j项指标下所占的比重pij:
| $ {{p}_{ij}}=\frac{{{x}_{ij}}}{\sum\limits_{i=1}^{m}{{{x}_{ij}}}} $ | (8) |
计算第i项指标的熵值ej:
| $ e_{j}=-\frac{1}{\ln m} \sum\limits_{i=1}^{m}\left(p_{i j} \ln p_{i j}\right), e \in[0, 1] $ | (9) |
计算第j项指标的差异性系数gj:
| $ g_{j}=1-e_{j} $ | (10) |
计算第j项指标的权重wj:
| $ {{w}_{j}}=\frac{{{g}_{j}}}{\sum\limits_{j=1}^{n}{{{g}_{j}}}} $ | (11) |
计算各项指标的综合评分Si:
| $ {{S}_{i}}=\sum\limits_{j=1}^{n}{{{w}_{j}}}{{x}_{ij}} $ | (12) |
计算得到新型城镇化各项指标的权重列于表 1 ①。
① 限于篇幅,中国省际新型城镇化水平具体测算未在正文中报告,感兴趣的读者可联系作者索取。
2.核心解释变量:制造业集聚
目前,学界关于产业集聚的测度方法主要集中于三大类:总体经济活动的测度方法、距离空间测度方法以及空间自相关法。由于本文测度的是基于省级层面的制造业集聚水平,不需要反映产业在可变空间范围内的集聚,因此本文选择基于总体经济活动的测度方法。基于总体经济活动的测度方法包括:区位熵、空间基尼系数、E-G指数以及M-S指数。对于特定区域内的产业集聚测度应选择区位熵;对于全国范围内产业集聚的测度应选择空间基尼系数、E-G指数以及M-S指数。对此,本文参考曾鹏、秦艳辉[27]和赵敏、马周剑[28]的方法,采用区位熵方法测度中国31省、直辖市和自治区的制造业集聚水平。测算公式为:
| $ \mathrm{L} \mathrm{Q}_{i}=\left(q_{i} / q\right) /\left(\mathrm{gdp}_{i} / \mathrm{gdp}\right) $ | (13) |
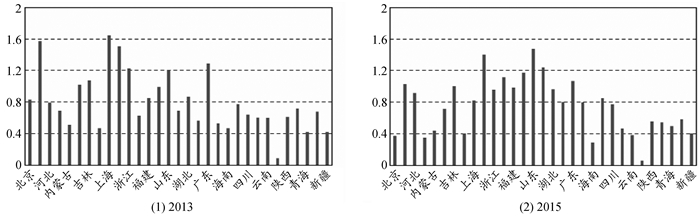
式(13)中,qi为地区i的制造业产值,q为全国制造业产值;gdpi为地区i的国内生产总值,gdp为全国国内生产总值。测算部分结果如图 1所示。
|
图 1 2003与2015年中国制造业集聚水平 |
通常,若区位熵大于1则表明某产业在该地区具有明显的专业化优势,产业集聚程度较高;若区位熵小于1则说明该产业专业化程度不足,产业集聚程度较低[29]。从图 1可以看出,天津、吉林、江苏、安徽、江西、山东、河南以及广东的制造业集聚程度最高,专业化优势明显。通过对比2003年和2015年可以发现,中国制造业集聚的空间分布具有稳定的特征。
3.控制变量
(1) 对外出口。随着全球经济一体化,出口贸易对新型城镇化的快速发展有一定影响作用。出口可以扩大对当地产品的需求,增加就业,促进经济发展。尤其是“一带一路”倡议实施以来,中国广泛参与国际竞争,为新型城镇化提供了强大动力。本文采用各省当年对外贸易经济中的出口额占GDP的比重来表示。
(2) 金融发展。现代金融作为市场经济的主要组成部分、社会资源配置的重要平台,将对中国城镇化进程产生重要影响。金融发展水平的提高能为城镇基础设施建设、公共服务供给、城镇产业发展和结构调整提供强有力的资金支持。本文选取各省当年金融机构贷款总额占GDP的比重来表示。
(3) 财政支出。政府在教育、科技、社保、就业等城镇公共服务上的财政支持也具有关键作用,尤其在基础设施建设和公共事业服务提升方面宏观统筹,直接影响着新型城镇化进程。借鉴宛群超等[30]的做法,本文选取各省当年政府公共预算财政支出占GDP的比重来表示。
(三) 数据来源与数据说明本文选取2003—2015年中国31省、直辖市和自治区的数据作为样本。所涉及的数据来源于《中国工业统计年鉴》《中国人口和就业统计年鉴》《中国教育统计年鉴》《中国科技统计年鉴》《中国高技术产业统计年鉴》《中国城市统计年鉴》《中国文化文物统计年鉴》《中国卫生和计划生育统计年鉴》《中国统计年鉴》以及各省(市)统计年鉴和统计公报。为消除异方差以及缩小数量级,本文对所有数据进行了对数处理。变量说明与描述性统计分别见表 2和表 3。
| 表 2 变量说明 |
| 表 3 变量描述性统计 |
基于式(2)和式(3),对中国31省、直辖市和自治区新型城镇化Moran’s I进行了全局空间自相关检验,结果如表 4所示:Moran’s I为0.644并且在1%的显著水平上显著为正。对此可以作出判断:中国31省、直辖市和自治区的新型城镇化水平在空间上存在依赖现象。
| 表 4 空间自相关检验 |
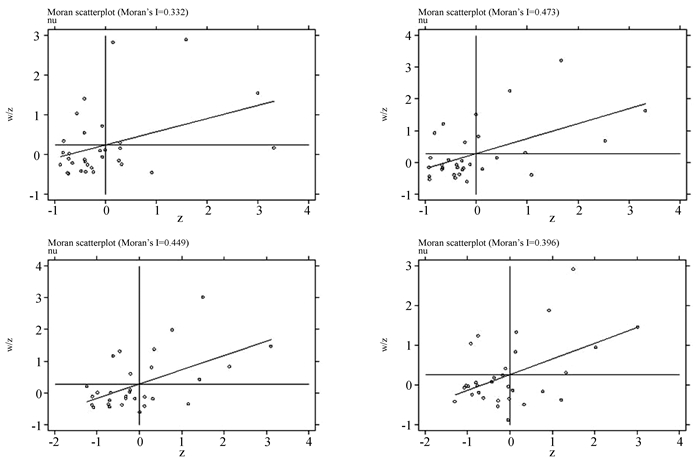
为进一步分析各地区的新型城镇化水平在空间上的异质性,本文选取了2003、2009、2012和2015年这4年的数据绘制了Moran’s I散点图。从图 2中可以看出,除少数几个省份外,其他绝大多数省份都处在一、三象限,这说明中国31省、直辖市和自治区的新型城镇化水平存在高度的正相关特征。通过对比这4年的Moran’s I散点图可以发现,除了少数几个省份存在变动的情况,其他绝大多数的省份散布在各象限的位置基本保持不变,这再次说明了新型城镇化表现出稳定的空间依赖特征。
|
图 2 中国新型城镇化Moran’s I |
本文进行了一系列检验以进行模型的筛选:Hausman检验表明模型应当设定为固定效应类型;空间滞后模型和空间误差模型的LM检验和Robust LM检验均显著拒绝不存在空间相关性的原假设,这表明空间计量方法的引入是合理的;空间杜宾模型条件下Wald检验和LR检验表明空间杜宾模型不能简化为空间滞后模型和空间误差模型,因此应当设定为空间杜宾模型;个体固定效应以及时间固定效应的LR检验均可以显著地拒绝无个体固定效应和无时间固定效应的原假设,这表明应当将模型设定为双固定效应模型。综上所述,本文将计量模型设定为双固定效应空间杜宾模型。对式(1)采用极大似然法进行估计,估计结果报告于表 5。
| 表 5 空间计量回归结果 |
如表 5所示,列(1)报告了式(1)各变量的点估计系数;列(2)—列(4)为采用偏微分方法基于式(5)对列(1)所报告的点估计系数进行的空间溢出效应分解,分别为直接效应、间接效应与总效应。由于总效应为直接效应与间接效应的加总,因此下文将主要关注对直接效应与间接效应的讨论。
首先关注本文的核心解释变量制造业集聚。制造业集聚的直接效应显著为正,这说明了制造业集聚对当地新型城镇化建设具有显著的推动作用,这验证了本文的假设1。制造业集聚,尤其是劳动密集型产业的集聚引致大量的劳动力需求,这吸纳了大量农村剩余劳动力流入城镇,进而推动人口城镇化。此外,在制造业大规模集聚的同时,传统服务业和现代服务业也获得了快速发展的机会[30],这推动生产要素在三次产业之间的流动更有效率、更合理,促进要素向城镇聚集,从而不断完善城镇配套公共服务。更重要的是,制造业集聚通过规模经济、基础设施、资源要素共享、技术和知识溢出发挥正的经济外部性[31],从而带动城市经济发展、提高城乡居民收入。其次,制造业集聚的间接效应显著为正,这说明了制造业集聚在推动本地区新型城镇化的同时,对周边地区产生了正向的溢出效应和示范效应,推动了周边地区的新型城镇化水平。究其原因,主要是在成本驱动下制造业集聚的规模效应使得企业的生产成本降低,推进了企业向该地区城镇的转移。同时,相关服务业的进入加快高端人才的聚集,从而推动产业结构升级。随着产业结构升级,产业结构趋于合理,要素成本开始上升,产业向周边地区扩散形成了区域产业联动发展,这就为周边地区的城镇化建设提供了产业基础,间接带动周边地区的城镇化发展。
控制变量的估计结果显示,对外出口的直接效应显著为正,间接效应为正但不显著,这说明随着各省出口的增加,不仅会推动本地区新型城镇化水平显著提高,还能在一定程度上带动邻接省份及全部地区的新型城镇化发展。出口一方面直接带动了地区经济的增长从而为新型城镇化的发展提供良好的基础,另一方面由出口所带来的就业效应不仅促进本地区农村剩余劳动力流入城镇,也促进了劳动力和其他资源要素的跨区域流动,对周边地区城镇化形成扩散效应。金融发展的直接效应显著为正,这表明金融发展是本地区新型城镇化的推动力量。金融的快速发展通过促进资本的有效配置,为城镇的发展提供资金支持,同时其通过发挥调节经济的杠杆作用推动产业结构不断优化从而提高城镇经济的竞争力。但是金融发展的间接效应不显著,表明本地区的金融发展对邻近地区不具有“示范效应”。此外,政府财政支出的直接效应、间接效应也显著为正,这与预期一致。就中国的情况看,基础设施建设、公共服务及房屋建设等城市化建设项目都依赖于政府的财政投入,政府在中国的社会发展和经济建设中都具有举足轻重的作用,政府财政的有力支持是持续发展的根本保障。
(三) 稳健性检验1.内生性检验
制造业集聚和新型城镇化之间可能由于存在双向因果关系导致模型存在内生性问题,本文采用工具变量法来检验制造业集聚的内生性。本文选择制造业集聚(lnagg)与其均值差值的三次方以及其滞后三期项作为工具变量[32-33],并对工具变量的有效性进行不可识别检验、弱工具变量检验以及过度识别检验,在此基础上对制造业集聚的内生性进行Hausman检验。
检验结果如表 6所示,不可识别检验在1%的显著水平上拒绝了工具变量不可识别的原假设;弱工具变量检验的统计值至少大于10%水平上的临界值;Sargen检验不能拒绝“所有工具变量均外生”的原假设。综上,本文所选择的工具变量是有效的。进一步,Hausman检验不能拒绝“不存在内生性”的原假设,这说明本文核心解释变量制造业集聚不存在内生性问题。
| 表 6 内生性检验 |
2.不同空间权重矩阵检验
本文研究的重点在于制造业集聚对新型城镇化的空间溢出效应,而空间溢出效应的测度受到空间权重矩阵选取的影响较大,针对不同空间权重矩阵下的估计进行稳健性估计是有必要的。因此,本文分别采用基于0-1邻接权重矩阵、地理距离、经济距离以及经济地理距离加权权重矩阵,并基于极大似然估计法对全样本下的空间杜宾模型进行估计,估计结果如表 7所示。结果发现:核心解释变量制造业集聚各项系数的符号方向及显著性均未发生改变,并且绝大多数控制变量的符号方向和显著性也保持了一致,这表明本文的估计结果是稳健的。
| 表 7 不同空间权重矩阵的估计 |
基于2003—2015年中国31省份的面板数据,本文考察了中国新型城镇化与制造业集聚的区域空间关联特征。通过构建空计量模型系统地分析了中国制造业集聚对新型城镇化的直接影响与空间溢出效应,研究结果表明:制造业集聚对新型城镇化的影响具有显著的推动作用,并且本地区制造业集聚对周边地区新型城镇化同样具有促进效应;增加财政支出有助于显著促进新型城镇化建设,并且空间溢出效应明显;对外出口、金融发展对本地区新型城镇化促进作用显著,但溢出效应却不明显。根据前文分析,本文给出如下政策启示。
第一,以产业集聚区作为城市功能外溢的核心地区,不断完善集聚区相关配套的基础设施和公共服务体系,实现要素资源禀赋的集聚和最优配置。第二,以人为本,着力解决发展与环境的矛盾,加大教育投入,提升人口素质,以此促进人口、土地和产业在城镇化进展中的协调发展。第三,强化地区之间的互动,不断推进产业协同和城市群的发展,促进产业集聚效率的有效提升和产业与城镇融合程度的不断提高。第四,推进金融等现代服务业的快速发展,以此促进资本的有效配置,为城镇的发展提供资金支持,同时其通过发挥调节经济的杠杆作用推动产业结构不断优化,从而提高城镇经济的竞争力。第五,加快产业结构转型升级,促进本土企业出口产品质量提升,以更好地成为新型城镇化的助推力。第六,对城镇化发展相对落后的地区,适当予以政策倾斜,并加大政府财政的投入力度,强化财政投入在新型城镇化中的重要地位,助推城镇建设的有效进行。
| [1] |
BUTTON K J. Urban economics:Theory and policy[J]. The Town Planning Review, 1978, 49(2): 247-248. |
| [2] |
BALDWIN J R, BROWN W M. Regional manufacturing employment volatility in Canada:The effects of specialisation and trade[J]. Papers in Regional Science, 2004, 83(3): 519-541. DOI:10.1111/j.1435-5597.2004.tb01923.x |
| [3] |
仇保兴. 简论我国健康城镇化的几类底线[J]. 城市规划, 2014, 38(1): 9-15. DOI:10.3969/j.issn.1000-3363.2014.01.002 |
| [4] |
苏雪串. 城市化进程中的要素集聚、产业集群和城市群发展[J]. 中央财经大学学报, 2004(1): 49-52. DOI:10.3969/j.issn.1000-1549.2004.01.012 |
| [5] |
胡伶俐, 施祖麟. 产业集聚推动城镇化发展机制研究——以桐乡市为例[J]. 特区经济, 2006(8): 362-364. DOI:10.3969/j.issn.1004-0714.2006.08.146 |
| [6] |
王亚飞, 廖甍, 董景荣. "先产后城"抑或"先城后产"?——来自中国省级面板数据的协整分析[J]. 重庆师范大学学报(社会科学版), 2019(1): 72-81. |
| [7] |
吴丰林, 方创琳, 赵雅萍. 城市产业集聚动力机制与模式研究进展[J]. 地理科学进展, 2010, 29(10): 1201-1208. DOI:10.11820/dlkxjz.2010.10.007 |
| [8] |
李华.基于产业空间集聚视角的中国城镇化发展研究[D].武汉: 武汉大学, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10486-1015026877.htm
|
| [9] |
MILLS E S, HAMILTON B W. Urban Economics[M]. New Jersey: Addison Wesley, 1997: 480.
|
| [10] |
罗薇薇. 产业集聚程度与城市化水平相关性的实证分析——以1988~2003年的广东省为例[J]. 兰州商学院学报, 2006, 22(2): 50-54. |
| [11] |
袁丹, 雷宏振. 高技术产业集聚与省域城镇化——基于空间面板模型的实证分析[J]. 科技进步与对策, 2015, 32(12): 45-49. DOI:10.6049/kjjbydc.2014110472 |
| [12] |
杨仁发, 李娜娜. 产业集聚能否促进城镇化[J]. 财经科学, 2016(6): 124-132. |
| [13] |
周敏, 刘志华, 孙叶飞, 等. 中国新型城镇化的空间集聚效应与驱动机制——基于省级面板数据空间计量分析[J]. 工业技术经济, 2018, 37(9): 59-67. DOI:10.3969/j.issn.1004-910X.2018.09.008 |
| [14] |
潘文卿. 中国区域经济发展:基于空间溢出效应的分析[J]. 世界经济, 2015, 38(7): 120-142. |
| [15] |
KRUGMAN P.Increasing returns and economic geography[R]. National Bureau of Economic Research, 1990.DOI: 10.3386/w3275.
|
| [16] |
孙振华.新型城镇化发展的动力机制及其空间效应[D].大连: 东北财经大学, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10173-1015565832.htm
|
| [17] |
谢治春. 制造业集聚与城镇化推进:基于省际面板数据的空间计量分析[J]. 当代经济科学, 2014, 36(4): 20-25, 124-125. DOI:10.3969/j.issn.1002-2848.2014.04.003 |
| [18] |
熊湘辉, 徐璋勇. 中国新型城镇化进程中的金融支持影响研究[J]. 数量经济技术经济研究, 2015, 32(6): 73-89. |
| [19] |
熊湘辉, 徐璋勇. 中国新型城镇化水平及动力因素测度研究[J]. 数量经济技术经济研究, 2018, 35(2): 44-63. |
| [20] |
ANSELIN L. Spatial econometrics:Methods and models[M]. Netherlands: Springer, 1988: 284.
|
| [21] |
范建双, 虞晓芬, 周琳. 城镇化、城乡差距与中国经济的包容性增长[J]. 数量经济技术经济研究, 2018, 35(4): 41-60. |
| [22] |
ELHORST J P. Spatial econometrics:From cross-sectional data to spatial panels[M]. Heidelberg: Springer-Verlag, 2014: 119.
|
| [23] |
韩峰, 谢锐. 生产性服务业集聚降低碳排放了吗?——对我国地级及以上城市面板数据的空间计量分析[J]. 数量经济技术经济研究, 2017, 34(3): 40-58. |
| [24] |
侯新烁, 张宗益, 周靖祥. 中国经济结构的增长效应及作用路径研究[J]. 世界经济, 2013, 36(5): 88-111. |
| [25] |
MORAN P A P. Notes on continuous stochastic phenomena[J]. Biometrika, 1950, 37(1/2): 17-23. DOI:10.2307/2332142 |
| [26] |
LESAGE J, PACE R K. Introduction to spatial econometrics[M]. New York: Chapman and Hall/CRC, 2009: 340.
|
| [27] |
曾鹏, 秦艳辉. 城市行政级别、产业集聚对外商直接投资的影响[J]. 国际贸易问题, 2017(1): 104-115. |
| [28] |
赵敏, 马周剑. 产业集聚与居民住房支付能力——基于省级面板数据的实证研究[J]. 南京审计大学学报, 2018, 15(6): 39-46. DOI:10.3969/j.issn.1672-8750.2018.06.005 |
| [29] |
林宏杰. 市场效应、政府行为与科技服务业集聚发展的空间视角分析——以福建省为例[J]. 重庆大学学报(社会科学版), 2018, 24(5): 1-17. |
| [30] |
宛群超, 杨晓岚, 邓峰. 外商直接投资如何影响省域创新效率——兼论环境规制的空间调节效应[J]. 科技管理研究, 2018, 38(5): 14-21. DOI:10.3969/j.issn.1000-7695.2018.05.003 |
| [31] |
贾兴梅, 贾伟. 中国制造业集聚对城市化的空间效应分析[J]. 财经科学, 2015(1): 79-89. DOI:10.3969/j.issn.1000-8306.2015.01.009 |
| [32] |
LEWBEL A. Constructing instruments for regressions with measurement error when no additional data are available, with an application to patents and R&D[J]. Econometrica, 1997, 65(5): 1201-1213. DOI:10.2307/2171884 |
| [33] |
黄凌云, 刘冬冬, 谢会强. 对外投资和引进外资的双向协调发展研究[J]. 中国工业经济, 2018(3): 80-97. |
 2019, Vol. 25
2019, Vol. 25


