2. 武汉大学 土木建筑工程学院, 武汉 430072;
3. 大连理工大学 土木工程学院, 大连 116024
2. School of Civil Engineering, Wuhan University, Wuhan, 430072, P. R. China;
3. School of Civil Engineering, Dalian University of Technology, Dalian 116024, P. R. China
中国80%的现役桥梁跨越水面,大约20万座桥梁的服役时间已超过25年,每年开工建设的桥梁约为1万座。桥墩处于复杂的三维水流环境中,局部冲刷易导致基础的承载力和稳定性降低,甚至失稳造成桥梁毁坏,冲刷是导致水毁的主要原因,是桥梁破坏的主要因素,60%的桥梁倒塌由冲刷造成,是超载损坏的6倍,是地震毁坏的30倍。由于冲刷发生在水下,导致桥梁损坏或破坏具有高隐蔽性,一旦破坏修复成本巨大,桥墩冲刷修缮的费用占桥梁维护费用的70%[1]。
传统的桥梁冲刷深度测量主要依靠人工检测,但水上作业严重威胁着检测人员的生命安全,且测量的准确性通常依赖检测人员的操作经验。近20年以来,桥梁冲刷监测逐渐受到国内外研究人员和学者的重视,目前正在使用和逐渐发展的冲刷监测方法大致有声呐、雷达、超声波、电磁波时域反射(time domain reflectometry,TDR)、光纤光栅等在线监测方法。声纳、雷达可确定泥沙淤积和冲刷的深度,探测装置较易安装[2, 3, 4],一般用于洪水过后的冲刷检查,但声纳和雷达的信号质量非常容易受泥沙颗粒或者水草等物的影响[5],在洪水期间,水流中含有大量泥沙和其他悬浊物时,监测的信号严重衰减,对于超声波存在同样的缺点[2]。另一方面,因声纳和雷达信号的测试、编译非常复杂,需要熟练的专业操作人员。TDR应用于桥梁冲刷监测时,通过冲刷导致相应部位的电缆变形甚至破坏,从而感知冲刷,但容易造成信号失真,影响测量结果[6]。将光纤光栅与特定的悬臂梁或其他杆件组合,布置在桥墩附近的河床,光纤光栅虽然直接或者间接地感知泥沙冲刷引起的土压力变化[7, 8, 9],但这种方法难以在恶劣服役环境下操作,并在定量方面存在困难。水下浮标和磁性定位环等作为一种冲刷监测技术,由于其监测到相应位置的冲刷后即告失效,缺乏一个长期有效、主动的服役周期[6]。
近些年,由于射频识别(radio frequency identification,RFID)技术的发展和应用,将RFID标签置于桥墩附近的河床,采用阅读器实时追踪RFID的三维位置信息判断冲刷深度和位置[10],但需要大规模地布置RFID,且仅有少量的RFID的三维位置信息反映冲刷坑的演变,因此RFID的三维运动缺乏针对性,不能主动跟踪冲刷坑的形成,同时,RFID标签价格昂贵,不适合大规模的工程应用。同样,采用微机电系统(micro-electro-mechanical systems,MEMS)的冲刷监测方法[11]存在与RFID类似的缺点。尽管如此,基于RFID或MEMS的实时定位系统在冲刷监测中的探索性研究是一项值得借鉴的在线监测技术。
磁测技术具有隐蔽性好、适应性强、不易受干扰等优点,目前逐渐应用到水下目标定位与导航、金属物探、水域探测、城市工程物探、考古及军事物探等方面。其中,磁场定位是应用最为广泛的磁测技术之一。为实现地磁定位,通常将地磁异常场反演为磁性目标。可通过测量磁性目标的磁感应强度及磁场梯度,计算磁测系统相对于目标的位置[12, 13],但目前测得的磁感应强度值包含地球背景磁场,且磁性目标的磁感应强度远小于地球磁感应强度,很难分离得到目标激发的磁感应强度。通过磁感应强度的三分量及磁场梯度,采用欧拉法的磁性目标定位[14, 15, 16],也存在磁性目标的磁感应强度与地球磁感应强度分离困难的问题。在远距离定位时,为避免目标的磁感应强度与地球背景磁场分离的问题,可采用磁场梯度通过优化的方法进行定位[17, 18]。优化搜索的目标函数是一个高度非线性的复杂多峰函数[17],受到非线性与不适定性的双重困扰,使得磁场梯度方程反演成为磁场梯度定位的难点问题。
磁测技术作为一种可穿透岩石、土体、淤泥和水流的非接触式监测技术,基于磁测技术的结构健康监测方法[18, 19]具有维护简便、可在恶劣环境中服役的优点,是一种值得深入研究的结构健康监测方法。文中针对磁性目标在运动时的磁性参数,采用运动自由度缩减的方式,解决基于优化搜索的磁场梯度反演中的非线性和不适定性的问题,利用桥墩局部冲刷机理,提出基于磁测技术的桥墩局部冲刷监测方法。采用磁性物质制作磁性标签石块,在桥墩前侧抛掷磁性标签石块,采用磁性标签石块和磁力梯度仪建立桥墩局部冲刷监测系统。通过磁场反演确定磁性标签石块的三维位移,实现桥墩局部冲刷监测,并通过模拟试验给予验证。
1 磁性标签石块的冲刷监测原理基于磁测技术探测磁性标签石块在冲刷坑中的三维位移场,跟踪磁性标签石块的运动。发生桥墩局部冲刷时,磁性标签石块随着冲刷坑的演变而移动。磁力梯度仪探测到磁性标签石块的三维位移场,根据磁性标签石块的位移场变化得到桥墩局部冲刷深度的变化,从而实现桥墩局部冲刷深度监测。
1.1 磁性标签石块的动态冲刷监测机理桥墩局部冲刷坑中,桥墩前侧的冲刷深度最大,因此,将磁性标签石块布置在桥墩前侧。桥墩局部冲刷坑可近似简化为三维漏斗[20],漏斗的倾角约为河床泥沙的休止角。对于墩前冲刷坑进一步简化为二维斜坡,则冲刷坑的发展可视为斜坡的扩展,磁性标签石块在水流作用下随着桥墩局部冲刷坑的加剧而运动,磁性标签石块的动态监测过程如图 1所示。

|
图1 磁性标签石块的冲刷监测示意图 Fig. 1 Scour monitoring of magnetic label rock |
平原河流流速一般小于3 m/s,山区河流最大流速可达5 m/s,近似取墩前行近流速为1~7 m/s。取磁性标签石块的容重为2.6 kN/m3,通过冲刷坑内的流场分析及磁性标签石块的稳定分析可得,当墩前行近流速为1~7 m/s,磁性标签石块直径为0.5 m时,磁性标签石块始终在墩前沿着冲刷坑向下运动[1, 21],可实现桥墩局部冲刷深度的动态监测。
1.2 磁性标签石块的冲刷位移场监测机理采用磁力梯度仪作为磁测仪器,在磁力梯度仪处的磁场梯度张量可视为磁性标签石块所激励,与地球磁场无关。当磁力梯度仪至磁性标签石块超过一定的距离时,可将磁性标签石块视为一个磁偶极子模型,则磁性标签石块在磁力梯度仪处的磁感应强度[22]为
| $B = \frac{{{\mu _0}}}{{4\pi }}\left[ {\frac{{3\left( {m \cdot r} \right)r}}{{{r^5}}} - \frac{m}{{{r^3}}}} \right],$ | (1) |
式中:μ0为介质磁导率;m(mx,my,mz)为磁性标签石块的磁矩;r=xi+yj+zk为磁性标签石块至磁力梯度仪的位矢,r=|r|。
磁感应强度B的梯度张量[23]为
| ${G_{ij}} = \frac{{\partial {B_i}}}{{\partial {r_j}}} = \frac{{{\mu _0}}}{{4\pi }}\left[ { - \frac{{15\left( {m \cdot r} \right){r_i}{r_j}}}{{{r^7}}} + \frac{{3{m_i}{r_j}}}{{{r^5}}} + \frac{{3{m_j}{r_i}}}{{{r^5}}} + \frac{{3\left( {m \cdot r} \right){\delta _{ij}}}}{{{r^5}}}} \right].$ | (2) |
| ${\delta _{ij}} = \left\{ {\begin{array}{*{20}{c}} 1&{i = j,}\\ 0&{i \ne j.} \end{array}} \right.$ | (3) |
如表示成空间3个方向(x,y,z)的变化率,则磁场梯度张量包括9个要素,即:
| $G = \left[ {\begin{array}{*{20}{c}} {\frac{{\partial {B_x}}}{{\partial x}}}&{\frac{{\partial {B_x}}}{{\partial y}}}&{\frac{{\partial {B_x}}}{{\partial z}}}\\ {\frac{{\partial {B_y}}}{{\partial x}}}&{\frac{{\partial {B_y}}}{{\partial y}}}&{\frac{{\partial {B_y}}}{{\partial z}}}\\ {\frac{{\partial {B_z}}}{{\partial x}}}&{\frac{{\partial {B_z}}}{{\partial y}}}&{\frac{{\partial {B_z}}}{{\partial z}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{B_{xx}}}&{{B_{xy}}}&{{B_{xz}}}\\ {{B_{yx}}}&{{B_{yy}}}&{{B_{yz}}}\\ {{B_{zx}}}&{{B_{zy}}}&{{B_{zz}}} \end{array}} \right].$ | (4) |
在无源空间中,磁感应强度的旋度为0,即▽×B=0,则磁场梯度张量为对称,Bxy-Byx=0,Bxz-Bzx=0,Byz-Bzy=0。磁感应强度的散度为0,即▽·B=0,则其迹traceG=Bxx+Byy+Bzz=0,故在磁场梯度张量的9个要素中,仅有5个要素是独立的,即Bxx,Bxy,Bxz,Byy,Byz。
磁场梯度张量G为实对称矩阵,可通过特征值转化为对角矩阵,其特征值的方程为
| ${\lambda ^3} - {I_0}{\lambda ^2} + {I_1}\lambda - {I_2} = 0,$ | (5) |
式中:I0,I1和I2分别为磁场梯度张量的不变量。
| ${I_0} = {B_{xx}} + {B_{yy}} + {B_{zz}} = 0,$ | (6) |
| ${I_1} = {B_{xx}}{B_{yy}} + {B_{xx}}{B_{zz}} + {B_{yy}}{B_{zz}} - B_{xy}^2 - B_{xz}^2 - B_{yz}^2,$ | (7) |
| ${I_2} = \det G = {B_{xx}}\left( {{B_{yy}}{B_{zz}} - B_{yz}^2} \right) + {B_{xy}}\left( {{B_{yz}}{B_{xz}} - {B_{xy}}{B_{zz}}} \right) + {B_{xz}}\left( {{B_{xy}}{B_{yz}} - {B_{xz}}{B_{yy}}} \right)$ | (8) |
磁场梯度张量的模量为
| ${C_T} = {\left[ {\sum {{{\left( {{G_{ij}}} \right)}^2}} } \right]^{0.5}} = {\left( {B_{xx}^2 + B_{yy}^2 + B_{zz}^2 + 2B_{xy}^2 + 2B_{xz}^2 + 2B_{yz}^2} \right)^{0.5}}.$ | (9) |
磁场梯度张量的不变量I1和I2可分辨磁性物质的边界,并快速反映与磁性标签石块的距离r。通过分析磁场梯度张量的不变量及磁场梯度张量的模量,可对桥墩冲刷深度进行早期预警。
磁性标签由钕铁硼磁铁和万向支架组成。磁性标签石块运动时,钕铁硼磁铁的方向角为(θ,φ),θ为磁偶极子的轴向与z轴的夹角,φ为磁偶极子的轴向在xoy平面的投影与x轴的夹角。磁性标签石块具有3个位置参数r(x,y,z)和3个磁矩参数m(mx,my,mz),即m(msin θcos φ,msin θsin φ,mcos θ)。因此,磁性标签石块在冲刷坑中运动时,钕铁硼磁铁本身具有5个自由度(x,y,z,θ,φ)。
钕铁硼磁铁置于万向支架的中心,钕铁硼磁铁的磁偶极子的轴向始终保持竖直,即θ=0。在磁性标签石块滚动、倾斜、旋转时,其磁矩参数m(mx,my,mz)可简化为m(0,0,m),从而消除了钕铁硼永磁铁的旋转自由度θ,φ。因此,钕铁硼永磁铁的运动简化为3个平动自由度r(x,y,z)。
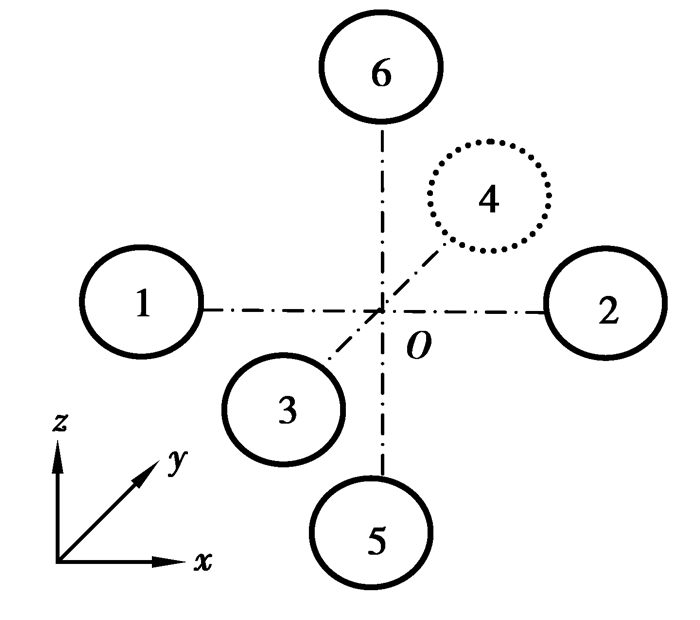
在实际磁场梯度测量系统中,一般通过多个三轴磁传感探头测量目标磁场,从而间接得到磁场梯度,文中磁传感探头中由6个三轴磁探头组合而成,可分别得到其三维磁感应强度,再计算得到磁场梯度,其空间位置如图 2所示。
|
图2 磁场探头的空间布置 Fig. 2 Arrangement of magnetometer |
| $B{'_{xx}} = \frac{{\partial {B_x}}}{{\partial x}} = \frac{{{B_{x1}} - {B_{x2}}}}{d},$ | (10) |
| $B{'_{yy}} = \frac{{\partial {B_y}}}{{\partial y}} = \frac{{{B_{y3}} - {B_{y4}}}}{d},$ | (11) |
| ${B_{zz}} = \frac{{\partial {B_z}}}{{\partial z}} = \frac{{{B_{z5}} - {B_{z6}}}}{d},$ | (12) |
| $B{'_{yz}} = B{'_{zy}} = 0.5\left( {\frac{{\partial {B_y}}}{{\partial z}} + \frac{{\partial {B_z}}}{{\partial y}}} \right) = \frac{{{B_{y5}} - {B_{y6}}}}{{2d}} + \frac{{{B_{z3}} - {B_{z4}}}}{{2d}},$ | (13) |
| $B{'_{xz}} = B{'_{zx}} = 0.5\left( {\frac{{\partial {B_x}}}{{\partial z}} + \frac{{\partial {B_z}}}{{\partial x}}} \right) = \frac{{{B_{z1}} - {B_{z2}}}}{{2d}} + \frac{{{B_{x5}} - {B_{x6}}}}{{2d}},$ | (14) |
| $B{'_{xy}} = B{'_{yx}} = 0.5\left( {\frac{{\partial {B_x}}}{{\partial y}} + \frac{{\partial {B_y}}}{{\partial x}}} \right) = \frac{{{B_{y1}} - {B_{y2}}}}{{2d}} + \frac{{{B_{x3}} - {B_{x4}}}}{{2d}},$ | (15) |
式中,Bxi、Byi、Bzi(i=1,…6)为各三轴磁传感探头处的磁感应强度,d为探头之间的基线距离。文中基线距离d取0.3 m。
通过万向支架,方程(2)中的未知数由(x,y,z,θ,φ)减少到r(x,y,z)。方程的非线性程度大幅度降低,可通过优化搜索的方式[12]求解r(x,y,z):
| $O\left( C \right) = \min {\left\{ {\frac{{\left[ {{{\left( {{B_{xx}} - B{'_{xx}}} \right)}^2} + {{\left( {{B_{xy}} - B{'_{xy}}} \right)}^2} + {{\left( {{B_{xz}} - B{'_{xz}}} \right)}^2} + {{\left( {{B_{yy}} - B{'_{yy}}} \right)}^2} + {{\left( {{B_{yz}} - B{'_{yz}}} \right)}^2}} \right]}}{5}} \right\}^{0.5}},$ | (16) |
式中,B′xx,B′xy,B′xz,B′yy和B′yz为磁力梯度仪测得的磁场梯度,Bxx,Bxy,Bxz,Byy,Byz为通过式(1)、式(3)~式(5)计算得到的磁场梯度,均含有未知的位矢r(x,y,z)。
磁性标签石块至磁力梯度仪的位矢r(x,y,z),与初始状态的位矢比较,得到磁性标签石块的位矢变化Δr(u,v,w),即可得到墩前冲刷坑的演变。
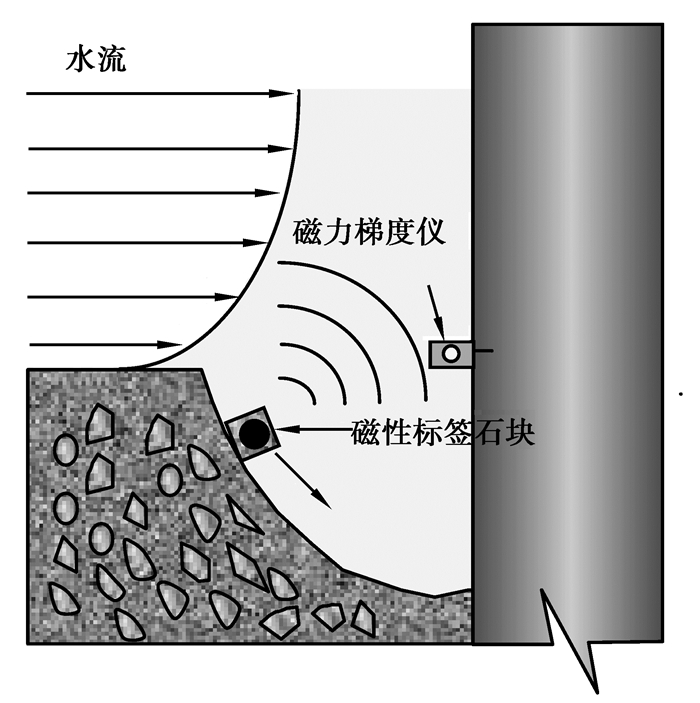
2 基于磁性标签石块的桥墩局部冲刷监测系统基于磁性标签石块的桥墩冲刷监测系统包括磁性标签石块和磁力梯度仪,如图 3所示。将磁性标签浇筑在混凝土中,即磁性标签石块。在桥墩前侧抛掷磁性标签石块,在桥墩前侧布置磁力梯度仪。
|
图3 桥梁局部冲刷监测系统 Fig. 3 Bridge local scour monitoring system |
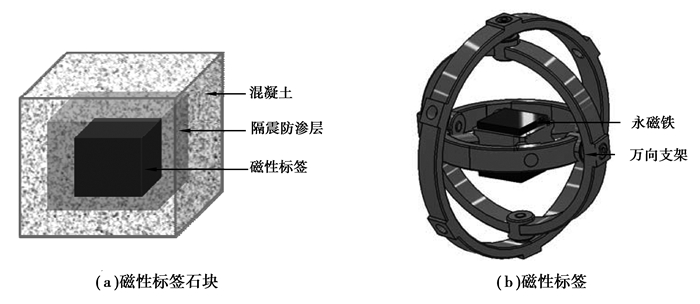
磁性标签石块由磁性标签、隔震防渗层和混凝土外壳组成,如图 4所示。为防止剧烈撞击导致磁性标签的磁性消失,采用橡胶作为隔震层;同时,采用电磁穿透率高、耐磨损、抗冲击的环氧工程塑料封装,作为磁性标签的防渗层。针对水环境中的各种化学性侵蚀、物理性撞击和磨损等,将封装好的磁性标签浇筑在混凝土石块中,即磁性标签石块。磁性标签包括钕铁硼永磁铁和万向支架,其中钕铁硼永磁铁置于万向支架的中心。
|
图4 磁性标签石块的结构 Fig. 4 Structure of magnetic label rock |
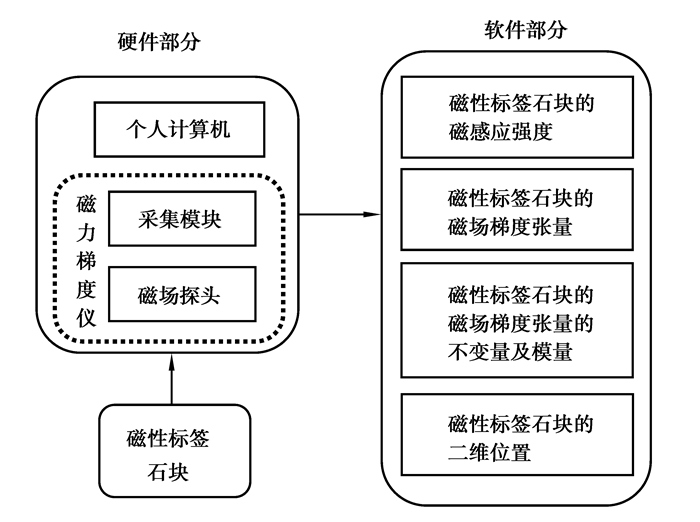
桥墩局部冲刷监测的系统集成如图 5所示。硬件部分包括磁性标签石块、磁力梯度仪和个人计算机,其中,磁力梯度仪包括磁场探头和数据采集模块。在软件部分中,得到随时间变化的磁性标签石块的磁感应强度后,根据前述的磁测原理,可依次得到磁性标签石块的磁场梯度张量、张量不变量及模量,并可计算反演得到磁性标签石块的三维位置变化。根据磁性标签石块的三维位移场变化,即可得到桥墩局部冲刷坑的演化过程。
|
图5 桥墩局部冲刷监测的系统集成 Fig. 5 System integration for bridge local scour monitoring |
磁性标签石块定位的模拟试验中,采用英国巴廷顿Mag-03低噪声版探头(分辨率为0.006 nT)和DAS1阵列式数据采集模块,在试验中,磁场梯度的测量通过多次调整磁场探头实现,采用激光测距仪测量实际位置。磁性标签石块采用烧结钕铁硼永磁铁,尺寸为70 mm×48 mm×24 mm,剩磁为1.23 T,矫顽力为860 kA/m,其磁矩约为m=9.58 A·m2。磁传感探头的中心设为坐标原点O(0,0,0),钕铁硼永磁铁的初始位置为P(0.5,0.5,2),则钕铁硼永磁铁至磁场探头的距离r=|OP|,磁矩为m(0,0,9.58)A·m2,模拟试验如图 6所示。

|
图6 磁性标签石块定位的模拟试验 Fig. 6 Experimental setup for magnetic localization of magnetic label rock |
钕铁硼永磁铁沿z轴从P0.5,0.5,2逐渐移动至P0.5,0.5,8,则钕铁硼永磁铁至磁场探头的距离为 $ r = \sqrt {0.5 + {z^2}} $。基于磁场梯度实测值,采用前述的磁场反演可得到钕铁硼永磁铁的三维位置。实际测量值(x,y,z)和反演值(x′,y′,z′)的对比见表 1。表 1中,误差 $\varepsilon = \sqrt {\left[{{{\left( {x - x'} \right)}^2} + {{\left( {y - y'} \right)}^2} + {{\left( {z - z'} \right)}^2}} \right]/3} $,相对误差 $\delta = r'/r = \left| {\sqrt {x{'^2} + y{'^2} + z{'^2}} - \sqrt {0.5 + {z^2}} } \right|/\sqrt {0.5 + {z^2}} $。
| 表1 磁性标签石块的定位误差 Table 1 Localization error for magnetic label rock |
从表 1可得,当钕铁硼永磁铁沿着z轴从P(0.5,0.5,2)移动至P(0.5,0.5,8)时,误差从0.017 m增大到0.207 m,相对误差δ从1.4 %增大到4.5 %。最大误差和最大相对误差分别小于0.2 m和5 %,其精度完全满足桥墩冲刷监测的要求。通过增大磁矩可提高监测距离,对于磁矩为15 Am的磁性目标和分辨率为0.2 nT的磁传感探头,最大探测距离可达到12 m,精度为0.3 m[17]。
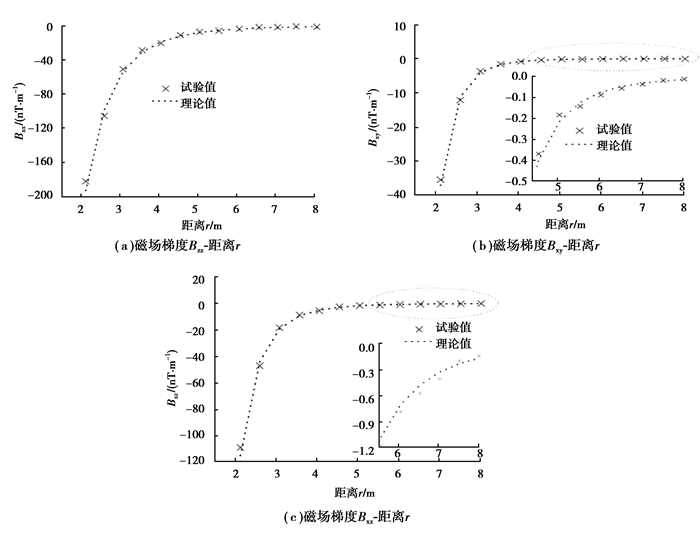
当钕铁硼永磁铁沿着z轴从P(0.5,0.5,2)移动至P(0.5,0.5,8)时,由于实验中Bxx=Byy=-0.5Bzz,Bxz=Byz,磁性标签石块至磁力梯度仪的距离r与冲刷深度直接相关,故仅分析磁场梯度Bzz,Bxy和Bxz随着距离r的关系,如图 7所示。
|
图7 磁场梯度与距离的关系 Fig. 7 Relation between magnetic gradient tensor and distance r |
从图 7可知,磁场梯度Bzz,Bxy和Bxz的绝对值随着距离r(冲刷深度)的增大而减小。磁场梯度的绝对值与(冲刷深度)距离直接相关,且试验值与理论值基本吻合。
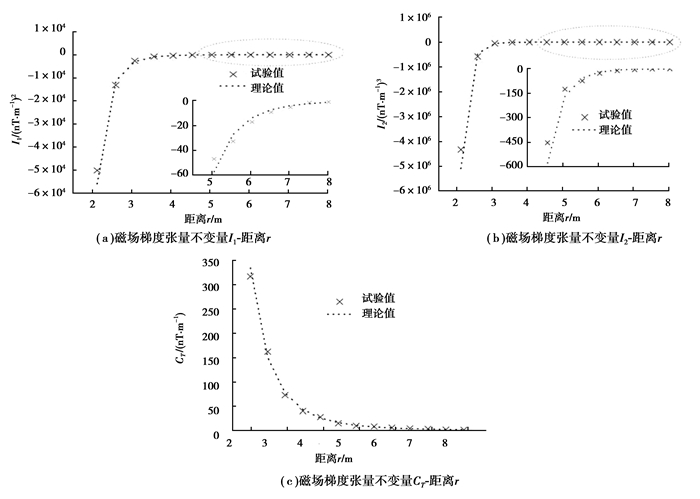
磁场梯度张量的不变量I1,I2及张量的模量CT与距离r的关系如图 8所示。
|
图8 磁场梯度张量不变量I1,I2和张量模量CT与距离r的关系 Fig. 8 Relation between I1,I2,CT and distance r |
从图 8可知,磁场梯度张量的不变量I1,I2的绝对值及磁场梯度张量的模量CT亦随着(冲刷深度)距离增大而减小,且试验值与理论值基本吻合。
磁场梯度、磁场梯度张量的不变量及张量的模量均与距离(冲刷深度)高度相关。故在桥墩冲刷监测中,可通过磁场梯度、磁场梯度张量的不变量及张量的模量进行初步的冲刷监测预警。磁场反演的计算可得到桥墩前侧冲刷位移场三维的位置r(x,y,z),可反映冲刷深度的长期演化规律。
4 结 论1)提出了一种基于磁性标签石块的桥墩局部冲刷监测方法。该冲刷监测系统包括内嵌磁性物质的磁性标签石块和磁力梯度仪,通过运动自由度缩减的方式,避免了基于优化搜索的磁场梯度反演中的非线性和不适定性的问题,采用磁场梯度反演磁性标签石块的三维位移场实现桥墩局部冲刷的实时监测。
2)磁性标签石块可直接抛掷在桥墩前侧,不需要布线,不受水流、泥沙、桥墩等的物理冲击和化学侵蚀的影响,也不需要维护,可长期服役、大规模、粗放式布设,适合洪水期间的桥墩冲刷监测。
3)在磁性标签石块的模拟定位试验中,最大误差为0.2 m,最大相对误差为5%,满足桥墩局部冲刷监测的要求。磁场梯度、磁场梯度张量不变量及张量的模量均与冲刷深度紧密相关,可直接用于桥墩局部冲刷监测的早期预警。
4)由于桥墩周围局部三维流场的复杂性,文中对桥墩局部流场和磁性标签石块的受力进行了简化,尚需要进一步的理论分析和试验验证。
| [1] | 江胜华,周智,欧进萍.基于赫兹接触理论的桥墩局部冲刷防护石块起动简化公式[J]. 中国公路学报,2014,27(5):118-124. JIANG Shenghua, ZHOU Zhi, OU Jinping. Simplified formula of riprap initiation for bridge local scour protection using hertz contact theory[J]. China Journal of Highway and Transport, 2014, 27(5): 118-124. (in Chinese)( 2) 2) |
| [2] | Hayden J T, Puleo J A. Near Real-Time Scour Monitoring System: Application to Indian River Inlet, Delaware[J]. Journal of Hydraulic Engineering, 2011, 137(9): 1037-1046.( 2) 2) |
| [3] | Falco F D, Mele R. The monitoring of bridges for scour by sonar and sedimetri[J]. NDT & E International, 2002, 35(2): 117-123.( 1) 1) |
| [4] | Deng L, Cai C S. Bridge Scour: Prediction, Modeling, Monitoring, and Countermeasures — Review[J]. Practice Periodical on Structural Design and Construction, 2010, 15(2): 125-134.( 1) 1) |
| [5] | Yu X B, Yu X. Assessment of an automation algorithm for TDR bridge scour monitoring system under various conditions[C].Transportation Research Board 88th Annual Meeting. January 11-15, 2009. [S.L.]: [s.n.], 2009.( 1) 1) |
| [6] | Yankielun N E, Zabilansky L. Laboratory investigation of time-domain reflectometry system for monitoring bridge scour[J]. Journal of Hydraulic Engineering, 1999, 125(12): 1279-1284.( 2) 2) |
| [7] | Lin Y B, Lai J S, Chang K C, et al. Flood scour monitoring system using fiber Bragg grating sensors[J]. Smart Materials and Structures, 2006, 15(6): 1950-1959.( 1) 1) |
| [8] | Lin Y B, Chen J C, Chang K C, et al. Real-time monitoring of local scour by using fiber Bragg grating sensors[J]. Smart Materials and Structures, 2005, 14(4): 664-670.( 1) 1) |
| [9] | Zhou Z, Huang M H, Huang L Q, et al. An optical fiber bragg grating sensing system for scour monitoring[J]. Advances in Structural Engineering, 2011, 14(1): 67-78.( 1) 1) |
| [10] | Lauth T J, Papanicolaou A N. Experimental/Feasibility Study of Radio Frequency Tracers for Monitoring Sediment Transport and Scour around Bridges[C]. Proceedings of the World Environmental and Water Resources Congress, Ahupua'a, 2008, 345-354.( 1) 1) |
| [11] | Lin Y B, Lai J S, Chang K C, et al. Using mems sensors in the bridge scour monitoring system[J]. Journal of the Chinese Institute of Engineers, 2010, 33(1): 25-35.( 1) 1) |
| [12] | Cattin V, Vial F, Maillot M C. Device and method for detecting the path of an object moving in two dimensions: US, US 8224618 B2[P]. 2012.( 2) 2) |
| [13] | 黄玉,郝燕玲.水下地磁异常反演中位置磁矩联合迭代算法[J].华中科技大学学报(自然科学版),2011,39(7):95-98. HUANG Yu, HAO Yanling. Iterative-combined algorithm of position and magnetic moment in underwater geomagnetic anomaly inversion localization[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2011, 39(7): 95-98. (in Chinese)( 1) 1) |
| [14] | Phillip W S. Inversion using Euler deconvolution of the magnetic gradient tensor[J]. AESC Extended Abstracts, 2006, 2006(1): 1-3.( 1) 1) |
| [15] | 张朝阳,肖昌汉.海底布放磁传感器的磁定位方法的模拟实验研究[J].上海交通大学学报(自然版),2011,45(6):826-830. ZHANG Zhaoyang, XIAO Changhan. Simulation experiment research for magnetic localization method for magnetometer sensor at seabed[J]. Journal of Shanghai Jiaotong University (Natural Science Edition), 2011, 45(6): 826-830. (in Chinese)( 1) 1) |
| [16] | Davis K, Li Y G, Nabighian M. Automatic detection of UXO magnetic anomalies using extended Euler deconvolution[J]. Geophysics, 2010, 75 (3): 13-20.( 1) 1) |
| [17] | Liu R H, Wang H. Detection and localization of improvised explosive devices based on 3-axis magnetic sensor array system[C]. 2010 Symposium on Security Detection and Information Processing, [S.L.]: Procedia Engineering, 2010(7): 1-9.( 2) 2) |
| [18] | 江胜华,周智,欧进萍.基于磁场梯度定位的边坡变形监测原理[J].岩土工程学报,2012,34(10):1944-1949. JIANG Shenghua, ZHOU Zhi, OU Jinping. Slope deformation monitoring principle based on magnetic gradient tensor[J]. Chinese Journal of Geotechnical Engineering, 2012, 34 (10): 1944-1949. (in Chinese)( 2) 2) |
| [19] | 江胜华,周智,欧进萍.基于磁测的边坡深部大变形监测方法[J].岩土力学,2013,34(10):3033-3038. JIANG Shenghua, ZHOU Zhi, OU Jinping. Slope internal large deformation monitoring using magnetic survey[J]. Rock and Soil Mechanics, 2013, 34 (10): 3033-3038. (in Chinese)( 1) 1) |
| [20] | Miller M J. Model for the time rate of local sediment scour at a cylindrical structure[D]. US: University of Florida, 2003.( 1) 1) |
| [21] | Richardson E V, Harrison L J, Richardson J R, et al. Evaluating Scour at Bridges[R]. 3th ed, Washington, DC: Federal Highway Administration, U.S. Department of Transportation, 1995.( 1) 1) |
| [22] | 张朝阳,肖昌汉,高俊吉,等.磁性物体磁偶极子模型适用性的试验研究[J].应用基础与工程科学学报,2010,18(5):862-868. ZHANG Zhaoyang, XIAO Changhan, GAO Junji, et al. Experiment research of magnetic dipole model applicability for a magnetic object[J]. Journal of Basic Science and Engineering, 2010, 18(5): 862-868. (in Chinese)( 1) 1) |
| [23] | Wynn W M. Magnetic dipole localization using the gradient rate tensor measured by a five-axis magnetic gradiometer with known velocity[C]. Detection Technologies for Mines and Minelike Targets, [S.L.]: SPIE Proceedings, 1995, 2496, 357-367.( 1) 1) |
 2016, Vol. 39
2016, Vol. 39

