2. 安徽科技学院 机械工程学院, 安徽 滁州 233100
2. College of Mechanical Engineering, Anhui Science & Technology University, Chuzhou 2331001, Anhui, P. R. China
行星齿轮传动具有体积小、重量轻、速比大、效率高等特点,在航空、船舶传动、汽车、起重机械及其他机械传动中获得了越来越广泛的应用,吸引了众多专家学者的研究目光[1, 2, 3, 4, 5]。齿轮副间存在的时变啮合刚度、齿侧间隙等因素,决定了行星齿轮传动系统强非线性的本质[6],文献[7, 8, 9, 10, 11, 12]的研究结论也证实了行星齿轮传动系统存在诸如运动状态的稳定性分岔、幅值跳跃等非线性动力学特征。
在工程实际中,机器的启动、停车以及工作状态的转换都会使得行星齿轮系统所传递的功率频繁变化,因而非常有必要研究行星齿轮传动系统随传递功率的分岔特性,以揭示传递功率的变化对其运动状态稳定性的影响规律,获得各种稳定的周期轨道与相应传递功率区间的映射关系。目前,有关行星齿轮传动系统分岔特性方面的研究还比较少见。文献[6]采用直接数值积分法,定性研究了行星齿轮传动系统随齿侧间隙等参数的全局分岔规律。文献[8]采用改进的PNF方法结合Floquet原理研究了行星齿轮传动系统的共存周期轨道的稳定性随转速的局部精细分岔规律。而关于行星齿轮传动系统随传递功率的分岔特性研究尚未见报道。
考虑到PNF(Poincaré-Newton-Floquet)方法需要在每次迭代计算前单独预估迭代初始值,计算效率较低,笔者将基于虞烈等[13]提出的CPNF(continuous Poincaré-Newton-Floquet)方法研究传递功率对行星齿轮传动系统周期轨道稳定性的局部精细分岔规律,并采用直接数值积分的方法绘制系统随功率的全局分岔图,以验证仿真结果的可靠性。
1 力学模型及振动微分方程本文力学模型采用文献[6]中的2K-H型行星齿轮传动系纯扭转非线性动力学模型,以下是该模型的简单介绍。2K-H型行星齿轮系统有1个太阳轮(以S表示),N个行星齿轮(第i个齿轮以pi表示),1个行星架(以C表示)和1个内齿圈(以R表示,固定于基础之上)组成,各齿轮为直齿圆柱齿轮,系统的扭转振动模型如图 1所示。

|
图1 系统扭转非线性振动模型 Fig. 1 Nonlinear vibration model of the system |
图中,太阳轮、行星架、第i个行星轮的角位移分别以θs、θc、θpi表示;太阳轮、第i个行星轮、内齿圈的基圆半径分别以rbs、rbpi、rbr表示;行星架半径以rc表示,其值为太阳轮与行星轮的节圆半径之和,标准安装下亦即太阳轮与行星轮的分度圆半径之和;太阳轮与第i路行星轮组成的外啮合副的啮合刚度、啮合阻尼系数、半齿侧间隙、综合啮合误差分别以kspi、cspi、bspi、espi表示;内齿圈与第i路行星轮组成的内啮合副的啮合刚度、啮合阻尼系数、半齿侧间隙、静传递误差分别以krpi、crpi、brpi、erpi表示,各齿轮的压力角均为α。
引入如下量纲一的参数$\Omega =\omega /{{\omega }_{n}}$, $\tau ={{\omega }_{n}}t$, ${{\omega }_{n}}=\sqrt{\frac{{{k}_{\text{msp}i}}}{{{m}_{\text{eq}1}}}}$, ${{m}_{\text{eq1}}}=\frac{{{m}_{\text{c}}}{{m}_{\text{s}}}}{{{m}_{\text{c}}}+{{m}_{\text{s}}}},$${{m}_{\text{eq2}}}=\frac{{{m}_{\text{c}}}{{m}_{\text{s}}}}{{{m}_{\text{c}}}+2{{m}_{\text{s}}}}$, ${{m}_{\text{s}}}=\frac{{{J}_{\text{s}}}}{r_{\text{bs}}^{2}}$, ${{m}_{\text{p}i}}=\frac{{{J}_{\text{p}i}}}{r_{\text{bp}i}^{2}}$, ${{m}_{\text{c}}}=\frac{{{J}_{\text{c}}}+\sum\limits_{i=1}^{3}{{{m}_{\text{p}i}}r_{\text{c}}^{2}}}{r_{\text{bc}}^{2}}$, $X=\bar{X}{{b}_{\text{c}}}$, $\dot{X}=\dot{\bar{X}}{{b}_{\text{c}}}{{\omega }_{n}}$, $\ddot{X}=\ddot{\bar{X}}{{b}_{\text{c}}}\omega _{n}^{2}$, $b={{b}_{\text{c}}}\bar{b}$, $e={{b}_{\text{c}}}\bar{e}$。其中,Js、Jpi、Jc分别为太阳轮转动惯量、第i个行星轮转动惯量、行星架转动惯量;bc为位移标称尺度,X表示相应齿轮副的啮合点相对位移;e表示相应齿轮副的静传递误差;ω表示齿轮的啮合频率,ωn表示固有频率;kmspi表示系统外啮合副的平均啮合刚度,字母上加“-”表示相应物理量量纲一的结果。
根据刚体平面运动微分方程并结合上述量纲一的参数,容易列写行星轮系的纯扭转量纲一的振动微分方程为
| $\left\{ \begin{align} & {{{\dot{\bar{X}}}}_{\text{sp}i}}+\frac{1}{\omega _{n}^{2}{{m}_{\text{eq}1}}}\sum\limits_{i=1}^{N}{\left[ {{k}_{\text{msp}i}}+{{k}_{\text{asp}i}}\sin \left( \tau \Omega +{{\varphi }_{\text{asp}i}} \right) \right]}f\left( {{{\bar{X}}}_{\text{sp}i}},{{{\bar{b}}}_{\text{sp}i}} \right)+ \\ & \frac{1}{\omega _{n}^{2}{{m}_{\text{p}i}}}\left[ {{k}_{\text{msp}i}}+{{k}_{\text{asp}i}}\sin \left( \tau \Omega +{{\varphi }_{\text{sp}i}} \right) \right]f\left( {{{\bar{X}}}_{\text{sp}i}},{{{\bar{b}}}_{\text{sp}i}} \right)+\frac{1}{\omega _{n}^{2}{{m}_{\text{p}i}}}{{c}_{\text{sp}i}}{{{\dot{\bar{X}}}}_{\text{sp}i}}- \\ & \frac{1}{\omega _{n}^{2}{{m}_{\text{p}i}}}\left[ {{k}_{\text{msp}i}}+{{k}_{\text{asp}i}}\sin \left( \tau \Omega +{{\varphi }_{\text{sp}i}} \right) \right]f\left( {{{\bar{X}}}_{\text{sc}}}-{{{\bar{X}}}_{\text{sp}i}}-{{{\bar{e}}}_{\text{sp}i}}-{{{\bar{e}}}_{\text{rp}i}},{{{\bar{b}}}_{\text{rp}i}} \right)+ \\ & \frac{1}{{{\omega }_{n}}{{m}_{\text{p}i}}}{{c}_{\text{rpp}i}}\left( {{{\dot{\bar{X}}}}_{\text{sc}}}-{{{\dot{\bar{X}}}}_{\text{sp}i}}-{{{\dot{\bar{e}}}}_{\text{sp}i}}-{{{\dot{\bar{e}}}}_{\text{rp}i}} \right)+\frac{1}{{{\omega }_{n}}{{m}_{\text{eq}1}}}\sum\limits_{i=1}^{N}{{{c}_{\text{sp}i}}}{{{\dot{\bar{X}}}}_{\text{sp}i}}+ \\ & \frac{1}{\omega _{n}^{2}{{m}_{\text{c}}}}\sum\limits_{i=1}^{N}{\left[ {{k}_{\text{mrp}i}}+{{k}_{\text{arp}i}}\sin \left( \tau \Omega +{{\varphi }_{\text{rp}i}} \right) \right]}f\left( {{{\bar{X}}}_{\text{sc}}}-{{{\bar{X}}}_{\text{sp}i}}-{{{\bar{e}}}_{\text{sp}i}}-{{{\bar{e}}}_{\text{rp}i}},{{{\bar{b}}}_{\text{rp}i}} \right)+ \\ & \frac{1}{{{\omega }_{n}}{{m}_{\text{c}}}}\sum\limits_{i=1}^{N}{{{c}_{\text{rp}i}}\left( {{{\dot{\bar{X}}}}_{\text{sc}}}-{{{\dot{\bar{X}}}}_{\text{sp}i}}-{{{\dot{\bar{e}}}}_{\text{sp}i}}-{{{\dot{\bar{e}}}}_{\text{rp}i}} \right)}=\frac{{{F}_{\text{D}}}}{\left( {{m}_{\text{s}}}{{b}_{\text{c}}}\omega _{n}^{2} \right)}+\frac{{{F}_{\text{L}}}}{\left( {{m}_{\text{c}}}{{b}_{\text{c}}}\omega _{n}^{2} \right)}-{{{\dot{\bar{e}}}}_{\text{sp}i}}\left( \tau \right){{{\dot{\bar{X}}}}_{\text{sc}}}+ \\ & \frac{1}{{{\omega }_{n}}{{m}_{\text{eq}2}}}\sum\limits_{i=1}^{N}{{{c}_{\text{sp}i}}{{{\dot{\bar{X}}}}_{\text{sp}i}}+\frac{2}{{{\omega }_{n}}{{m}_{\text{c}}}}\sum\limits_{i=1}^{3}{{{c}_{\text{rp}i}}}\left( {{{\dot{\bar{X}}}}_{\text{sc}}}-{{{\dot{\bar{X}}}}_{\text{sp}i}}-{{{\dot{\bar{e}}}}_{\text{sp}i}}-{{{\dot{\bar{e}}}}_{\text{rp}i}} \right)+} \\ & \frac{2}{\omega _{n}^{2}{{m}_{\text{c}}}}\sum\limits_{i=1}^{N}{\left[ {{k}_{\text{mrp}i}}+{{k}_{\text{arp}i}}\sin \left( \tau \Omega +{{\varphi }_{\text{rp}i}} \right) \right]}f\left( {{{\bar{X}}}_{\text{sc}}}-{{{\bar{X}}}_{\text{sp}i}}-{{{\bar{e}}}_{\text{sp}i}}-{{{\bar{e}}}_{\text{rp}i}},{{{\bar{b}}}_{\text{rp}i}} \right)= \\ & \frac{{{F}_{\text{D}}}}{\left( {{m}_{\text{s}}}{{b}_{\text{c}}}\omega _{n}^{2} \right)}+\frac{{{F}_{\text{L}}}}{\left( {{m}_{\text{c}}}{{b}_{\text{c}}}\omega _{n}^{2} \right)}AAA \\ \end{align} \right.$ | (1) |
方程(1)中,f表示相应齿轮副上的间隙非线性函数;kmrpi表示系统内啮合副的平均啮合刚度;kaspi表示系统外啮合副刚度波动幅值;karpi表示系统内啮合副刚度波动幅值;φspi表示系统第i路外啮合副刚度波动初相位;φrpi表示系统第i路内啮合副刚度波动初相位;FD为作用在太阳轮上的等效扭矩,FL为作用在行星架上的等效扭矩。
2 CPNF方法CPNF[13, 14]法是将确定参数下用来判断系统周期轨道稳定性的PNF方法与参数延续算法相结合形成的一种计算方法。这种方法利用预测校正原理,根据上一个参数值下求得的周期轨道对下一个参数值下的迭代初始值进行预估,很好地解决了迭代的初始值问题。该方法的另一优点是在迭代计算周期轨道的过程当中可以同步获得周期轨道的状态转移矩阵,使周期轨道的求解与稳定性判断工作可以同步进行,因而大大提高了周期轨道稳定性局部分岔的计算效率。
对于如下含有参数ω的n维非线性动力系统
| $\dot u = f\left( {u,\omega ,t} \right),\left( {u,\omega ,t} \right) \in {\rm{R}} \times {\rm{R}} \times {{\rm{R}}^n}。$ | (2) |
应用庞加莱映射,可以把求解该非线性动力系统周期解曲线的问题转变为求解点映射系统
| ${u^{\left( {k + 1} \right)}}\left( \omega \right) = P\left( {\omega ,{u^{\left( k \right)}}} \right)$ | (3) |
在庞加莱截面上的不动点
| ${u^*}\left( \omega \right) = P\left( {\omega ,{u^*},\left( \omega \right)} \right)$ | (4) |
的问题,即求解非线性代数方程
| $Q\left( {\omega ,u} \right) = u - P\left( {\omega ,u} \right) = 0$ | (5) |
的解曲线问题。CPNF方法将该问题的求解过程分成了预测和校正两步。
2.1 预测假设已经求得ω=ωk时周期解在庞加莱截面上的不动点uk,那么采用欧拉型积分公式,可以得到如下预测公式
| $\left\{ \begin{array}{l} u_{\left( {k + 1} \right)}^0 = {u_k} - {\left[ {{Q_u}'\left( {{\omega _k},{u_k}} \right)} \right]^{ - 1}} \times {Q_\omega }'\left( {{\omega _k},{u_k}} \right) \times \Delta \omega = \\ {u_k} - {\left[ {E - {P_u}'\left( {{\omega _k},{u_k}} \right)} \right]^{ - 1}} \times {P_\omega }'\left( {{\omega _k},{u_k}} \right) \times \Delta \omega {\omega _{\left( {k + 1} \right)}} = \\ {\omega _k} + \Delta \omega , \end{array} \right.$ | (6) |
式中:P′u(ωk,uk)=DP(ωk,uk)为当参数取ω=ωk时Poincaré映射(3)在uk处的Jacobi矩阵;P′ω(ωk,uk)为Poincaré映射(3)在参数ω=ωk处的梯度向量;P′u(ωk,uk)及P′ω(ωk,uk)可以在第k步校正过程中获得,u(k+1)0为第(k+1)步校正计算的迭代初始值。
2.2 校正第k步校正过程实际就是利用PNF方法求解参数ω=ωk时系统周期解的牛顿迭代过程,不同的是,牛顿迭代的初始值已经由前一步的预测过程给出,而不需要由计算者人为给定,从而大大提高了求解的成功率,节省了计算时间。其系统第k步周期解的迭代公式为
| $u_k^{\left( {i + 1} \right)} = u_k^{\left( i \right)} - {\left[ {DP\left( {{\omega _k},u_k^{\left( i \right)}} \right) - E} \right]^{ - 1}}\left[ {P\left( {{\omega _k},{u_{k\left( i \right)}}} \right) - u_k^{\left( i \right)}} \right],$ | (7) |
其中,DP(ωk ,uk(i))以及P(ωk,uk(i))由联立微分方程组
| $\left\{ \begin{array}{l} \dot \phi = D{f_u}\left( {u,{\omega _k},t} \right)\left| {_{u = uk}\varphi ,\varphi \in {{\rm{R}}^{n \times n}},} \right.\\ \dot u = f\left( {u,{\omega _k},t} \right), \end{array} \right.$ | (8) |
以(E,uki)为初始值积分一个庞加莱映射周期T得到。式(8)中Dfu(u,ω,t)为非线性动力系统(2)的Jacobi矩阵。当利用公式(7)迭代求出满足精度要求的第k步周期解uk时,就同时得到了相应的状态传递矩阵DP(ωk,uk),可以用于周期解uk的稳定性分析以及第(k+1)步的预测。
为了实现第(k+1)步的预测,还需要计算梯度向量P′ω(ωk,uk),可以通过如下微分方程组
| $\left\{ \begin{array}{l} \dot \psi = D{f_u}\left( {u,\omega ,t} \right)\psi + D{f_\omega }\left( {u,\omega ,t} \right),\psi \in {{\rm{R}}^n},\\ \dot u = f\left( {u,{\omega _k},t} \right), \end{array} \right.$ | (9) |
由以(0,uk)为初始值积分一个庞加莱映射周期T,即可得到(P′ω(ωk,uk),P(uk))。式(9)中,Dfω(u,ω,t)为非线性动力系统(2)的关于参数ω的梯度向量。
3 行星齿轮传动系随传递功率的分岔规律以下运用CPNF方法研究行星齿轮非线性系统的传递功率P在196~220 kW变化时,系统周期运动稳定性的分岔特性。行星齿轮系统的基本参数如下:模数m=1.75 mm,压力角α=20°,太阳轮齿数zs=24,行星轮齿数zpi=39,内齿圈齿数zr=106,标称尺度bc=10 μm,行星轮个数N=3,内外啮合副齿侧间隙bspi=brpi=50 μm,量纲一的转速Ω=0.958 6。
CPNF方法在进行校正时,涉及到计算非线性动力系统(1)对应状态方程的Jacobi矩阵Dfu(u,ω,t)。考虑到纯扭转非线性动力学模型的非光滑性,Jacobi矩阵Dfu(u,ω,t)采用有限差分形式近似代替[14]。
3.1 周期一轨道随功率的稳定性分岔当传递功率P=220 kW时,经PNF方法计算,只获得了一个稳定的周期一不动点P1(0.993 218 5,-2.647 681 1,5.401 011 1,-1.933 860 6),其轨道相图如图 2所示。

|
图2 P=220 kW时稳定的周期一轨道 Fig. 2 Stable phase thajectory of P1 when P=220 kW |
由此考虑在小于P=220 kW的某段功率区间内,系统的运动可能以周期一轨道的形态稳定运行,为了确定周期一轨道保持稳定的功率范围以及具体的失稳分岔点功率值,以下通过CPNF方法计算了周期一轨道的Floquet乘子的最大模随功率P的变化曲线,如图 3所示。

|
图3 周期一轨道最大Floquet乘子模随功率的变化曲线 Fig. 3 The changing curve of P1 Floquet multiplier with power |
从图 3中可以看到,在P为211~220 kW范围内,周期一轨道的Floquet乘子的最大模小于1,即运动状态能够保持稳定;在P为196~211 kW范围内,Floquet乘子的最大模大于1,即周期一运动依然存在,但已经发生了Lyapunov意义下的失稳[15],变成不稳定的运动形态。由此可确定,周期一轨道稳定性的分岔功率为P=211 kW。
为了确定周期一轨道的稳定性在P=211 kW处具体的分岔途径,笔者模拟了在功率P=211 kW前后,周期一轨道具有最大模的Floquet乘子穿出复数域上单位圆的途径,如图 4所示,图中箭头方向指示了当传递功率由大变小时,周期一轨道Floquet乘子的变化走向。显然,Floquet乘子是由实轴负半轴穿出单位圆的,根据周期轨道分岔理论[15],当传递功率由大变小经过分岔点功率P=211 kW时,周期一轨道会发生倍周期分岔而失稳裂变成周期二轨道。
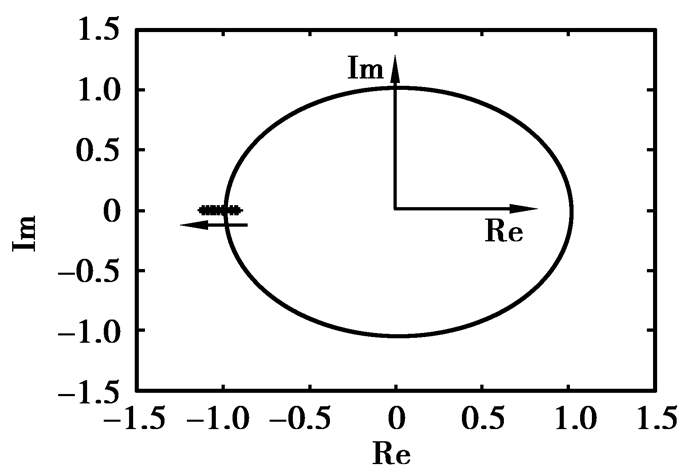
|
图4 周期一轨道Floquet乘子随功率穿出单位圆的途径 Fig. 4 The way across the unit circle of P1 Floquet multiplier |
由以上周期一运动的稳定性分岔分析可知,在小于211 kW的某个功率区间内,系统的运动将会以稳定的周期二轨道的形态存在。
当传递功率P=211 kW时,经PNF方法计算,获得了一个不稳定的周期一不动点P1(1.122 263 389 05,-2.681 586 539 89,5.462 945 802 425,-1.903 188 660 61)和一个稳定的周期二不动点P2(0.956 373 419 33,-2.724 380 076 71,4.664 356 134 64,-1.953 595 730 27),其周期轨道相图分别如图 5和图 6所示。

|
图5 P=211 kW时不稳定的周期一轨道 Fig. 5 Unstable phase thajectory of P1 when P=211 kW |
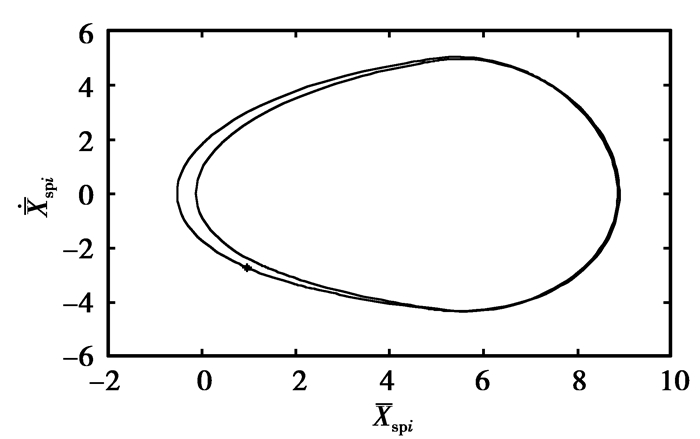
|
图6 P=211 kW时稳定的周期二轨道 Fig. 6 Stable phase thajectory of P2 when P=211 kW |
以上计算结果验证了CPNF方法关于周期一轨道在P=211 kW处发生倍周期分岔的预测。为了确定周期二轨道保持稳定状态的功率范围以及具体的失稳分岔点功率值,通过CPNF方法计算的周期二运动的Floquet乘子的最大模随功率P的变化曲线如图 7所示。

|
图7 周期二轨道最大Floquet乘子模随功率的变化曲线 Fig. 7 The changing curve of P2 Floquet multiplier with power |
从图 7中可以看到,在P为205.8~211 kW范围内,周期二轨道的最大Floquet乘子模小于1,即运动状态能够保持稳定;在P为196~205.8 kW范围内,最大Floquet乘子模大于1,即周期二运动依然存在,但已经发生了Lyapunov意义下的失稳[9],变成了不稳定的运动形态。由此可以确定,周期二轨道稳定性的分岔功率为P=205.8 kW。
为了确定周期二轨道稳定性在P=205.8 kW时具体的分岔途径,笔者模拟了功率由大变小经过P=205.8 kW时,周期二轨道具有最大模的Floquet乘子穿出复数域上单位圆的途径,如图 8所示。显然,Floquet乘子是由实轴负半轴穿出单位圆的,根据周期轨道分岔理论[15],当传递功率由大变小经过分岔点功率P=205.8 kW时,周期二轨道会发生倍周期分岔而失稳裂变成周期四轨道。

|
图8 周期二轨道Floquet乘子随功率穿出单位圆的途径 Fig. 8 The way across the unit circle of P2 Floquet multiplier |
由以上周期二运动的稳定性分岔分析可知,在小于205.8 kW的某个功率范围内,系统的运动将会以稳定的周期四轨道的形态存在。
当传递功率为205.8 kW时,经PNF方法计算,获得了一个不稳定的周期一不动点P1 (1.246 607 377 329,-2.707 429 571 563,5.523 882 489 132,-1.867 422 471 809)、一个不稳定的周期二不动点P2 (2.098 566 305 065,-2.734 138 541 796,8.311 191 163 223,-1.323 076 184 707)和一个稳定的周期四不动点P4(2.797 053 954 0,-2.606 852 968 25,8.572 761 368 432 6,-1.587 082 095 98),其周期轨道相图分别如图 9~11所示。

|
图9 P=205.8 kW时不稳定的周期一轨道相图 Fig. 9 Unstable phase thajectory of P1 when P=205.8 kW |

|
图10 P=205.8kW时稳定的周期二轨道相图 Fig. 10 Unstable phase thajectory of P2 when P=205.8 kW |
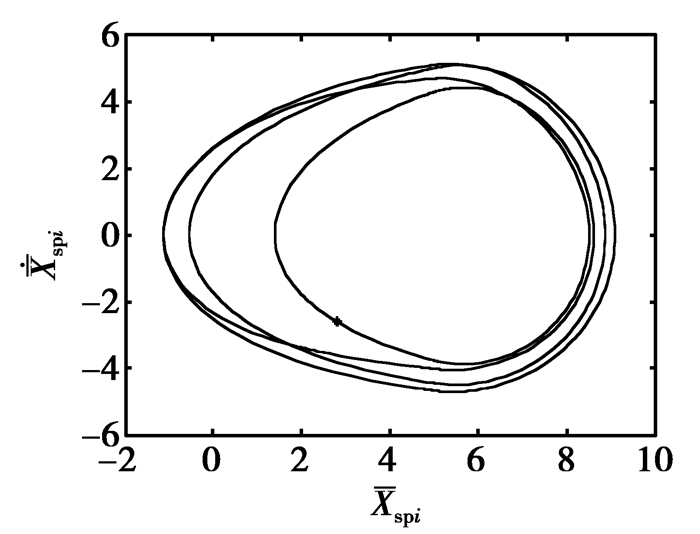
|
图11 P=205.8 kW时不稳定的周期四轨道相图 Fig. 11 Stable phase thajectory of P4 when P=205.8 kW |
以上计算结果验证了CPNF方法关于周期二轨道在P=205.8 kW处发生倍周期分岔的预测。为了确定周期四轨道保持稳定的功率范围以及具体的失稳分岔点功率,以下通过CPNF方法计算了周期四轨道的Floquet乘子的最大模随功率P的变化曲线,如图 12所示。
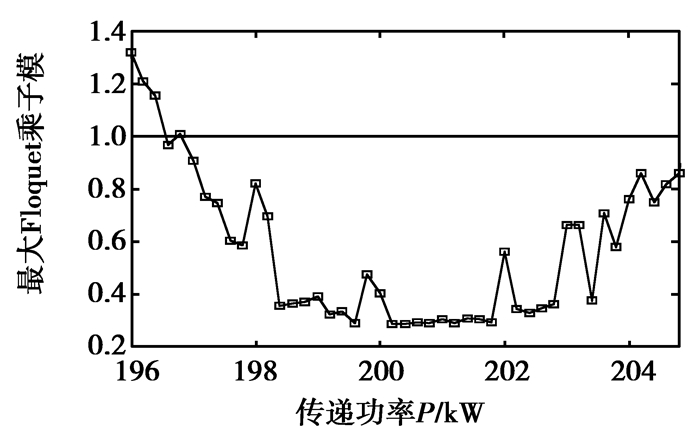
|
图12 周期四轨道最大Floquet乘子模随功率的变化曲线 Fig. 12 The changing curve of P4 Floquet multiplier with power |
从图 12中可以看到,在196.8~205.8 kW范围内,周期四轨道Floquet乘子的最大模小于1,即运动状态能够保持稳定;在196.0~196.8 kW范围内,Floquet乘子的最大模大于1,即周期四轨道依然存在,但已经发生了Lyapunov意义下的失稳[15],变成不稳定的运动形态。由此可确定,周期四轨道稳定性的分岔功率为P=196.8 kW。
为了确定周期四轨道稳定性在P=196.8 kW时具体的分岔途径,笔者模拟了功率由大变小经过P=196.8 kW时,周期四轨道具有最大模的Floquet乘子穿出复数域上单位圆的途径,如图 13所示。显而易见,Floquet乘子是由实轴负半轴穿出单位圆的,也就是说随着功率的由大变小,周期四轨道在P=196.8 kW处会发生倍周期分岔而失稳裂变成周期八轨道[15]。
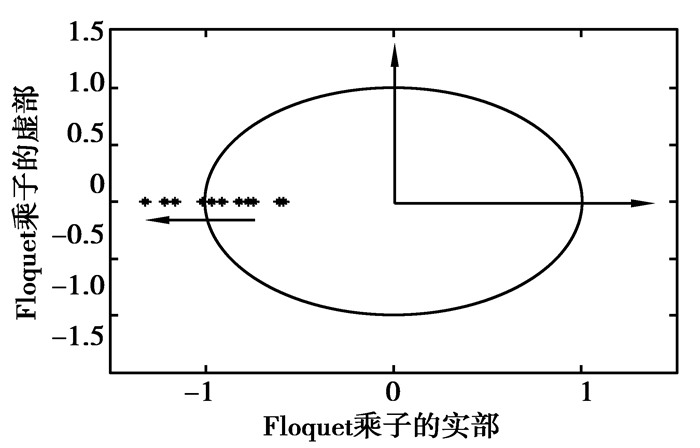
|
图13 周期四轨道Floquet乘子随功率穿出单位圆的途径 Fig. 13 The way across the unit circle of P4 Floquet multiplier |
当传递功率为196.0 kW时,采用PNF方法计算获得了如下4个共存的周期不动点:
P1(1.326 969 56,-2.720 465 9,5.563 583 4,-1.840 685 9);
P2(2.478 602 02,-2.779 455 9,8.898 100 5,-0.994 215 5);
P4(-0.007 560 10,-2.361 369 9,2.470 765 6,-1.816 708 5);
P8(3.313 389 72,-2.629 371 0,8.819 356 8,-1.698 036 1)。
同时得到了以上各周期不动点的状态转移矩阵P1、P2、P4、P8。
| $\begin{array}{l} {P_1} = \left[ {\begin{array}{*{20}{c}} { - 0.580\;1}&{ - 2.361\;1}&{ - 0.004\;9}&{0.388\;2}\\ {0.428\;3}&{0.561\;7}&{ - 0.142\;2}&{ - 0.258\;8}\\ {0.284\;2}&{0.626\;8}&{ - 0.931\;9}&{ - 2.448\;1}\\ {0.185\;0}&{0.772\;0}&{ - 0.088\;5}&{ - 0.843\;3} \end{array}} \right],\\ {P_2} = \left[ {\begin{array}{*{20}{c}} { - 0.638\;3}&{ - 2.506\;3}&{ - 0.001\;3}&{0.404\;4}\\ {0.385\;7}&{0.453\;6}&{ - 0.135\;1}&{ - 0.235\;3}\\ {0.250\;3}&{0.549\;0}&{ - 0.937\;0}&{ - 2.459\;4}\\ {0.203\;6}&{0.858\;2}&{ - 0.140\;0}&{ - 0.992\;5} \end{array}} \right],\\ {P_4} = \left[ {\begin{array}{*{20}{c}} {1.114\;0}&{ - 1.678\;5}&{ - 0.591\;1}&{2.504\;6}\\ {0.012\;5}&{0.472\;4}&{0.029\;1}&{ - 0.487\;8}\\ { - 1.238\;8}&{1.466\;0}&{0.471\;4}&{ - 2.416\;0}\\ { - 1.575\;5}&{2.191\;9}&{0.724\;2}&{ - 3.459\;8} \end{array}} \right],\\ {P_6} = \left[ {\begin{array}{*{20}{c}} {00.071\;0}&{ - 0.265\;3}&{ - 0.043\;4}&{0.265\;8}\\ {0.225\;1}&{ - 0.404\;8}&{ - 0.014\;4}&{0.551\;8}\\ { - 0.007\;6}&{0.808\;6}&{0.171\;3}&{ - 1.040\;5}\\ {0.118\;2}&{0.355\;7}&{0.104\;2}&{ - 0.415\;7} \end{array}} \right]。 \end{array}$ |
进一步分析以上4矩阵的特征值模的最大值,亦即Floquet乘子模的最大值,分别为λ(P1)=1.278 438 866,λ(P2)=1.605 355 509,λ(P4)=1.320 196 013 62,λ(P8)=0.691 605 07,显然在该组参数下只有周期八运动稳定。
3.5 周期运动稳定性随传递功率的分岔特性总结以上分析,可以大致勾勒出传递功率在196.0~220.0 kW范围内系统周期运动状态稳定性的分岔情况,如图 14所示。图中实线表示稳定的周期运动,点划线表示不稳定周期运动。作为对比,笔者采用直接数值积分的方法绘制了行星齿轮传动系统随功率的全局分岔图,如图 15所示。可以发现在功率区间196.0~220.0 kW内,两图所显示的分岔规律以及分岔点功率值非常吻合。需要指出的是,基于CPNF方法预测的局部分岔图可以获得所有共存周期轨道(包括不稳定的周期轨道)的分岔规律,而基于直接数值积分的全局分岔图只能显示渐进稳定的周期轨道之间的分岔关系,这是CPNF方法预测的局部分岔图的优点之一。此外,由于局部分岔图中14所显示的分岔点参数是由Floquet乘子定量判断而得,所以比全局分岔图 15定性显示的分岔点参数值更加精确。
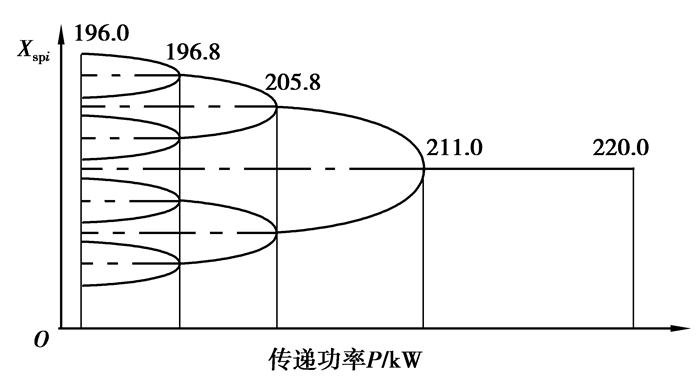
|
图14 周期运动稳定性随传递功率的局部分岔图 Fig. 14 The local bifurcation diagram with power |
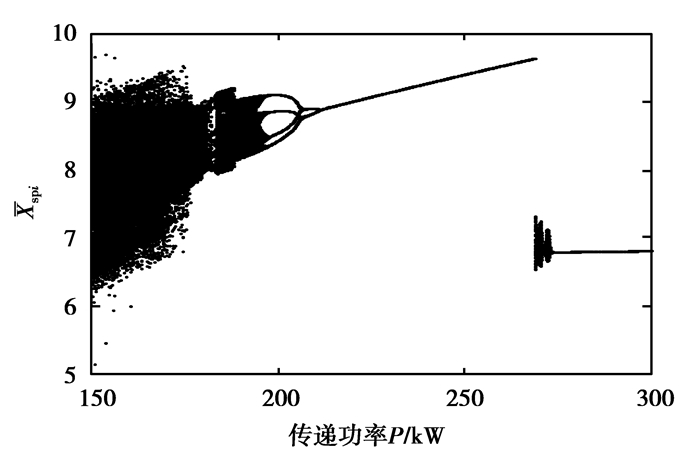
|
图15 行星齿轮系统随传递功率P的全局分岔图 Fig. 15 The global bifurcation diagram with power |
从分岔图 14中可以看到,在功率196.0~196.8 kW范围内,行星齿轮非线性系统共存一个不稳定的周期一运动、一个不稳定的周期二运动、一个不稳定的周期四运动和一个稳定的周期八运动;在功率196.8~205.8 kW范围内,行星齿轮非线性系统共存一个不稳定的周期一运动、一个不稳定的周期二运动和一个稳定的周期四运动;在功率205.8~211.0 kW范围内,行星齿轮非线性系统共存一个不稳定的周期一运动和一个稳定的周期二运动;在功率211.0~220.0 kW范围内,行星齿轮非线性系统呈现单一而稳定的周期一运动。
总而言之,在传递功率196.0~220.0 kW范围内,随着功率值的逐渐增大,行星齿轮传动系统的各周期轨道均是通过倍周期倒分岔的途径在相应功率分岔点处发生稳定性突变的。全局分岔图 15显示,经过充分的倍周期分岔后,在小于196.0 kW的某个功率值上,行星齿轮非线性系统会呈现混沌运动状态。
4 结 论1) 采用CPNF方法研究获得的行星齿轮传动系统的周期运动轨道稳定性随传递功率的局部分岔规律,与通过直接数值积分法得到的的全局分岔规律基本吻合,证明了CPNF方法在研究行星齿轮传动系统分岔特性方面的有效性。
2) 在某些确定的参数组合下,行星齿轮传动系统会共存多个周期轨道,这些轨道有的稳定,有的不稳定;随着功率值的逐渐增大,行星齿轮传动系统的渐进稳定的周期轨道会通过倍周期倒分岔的途径发生失稳;在轻载工况下,行星齿轮非线性系统容易呈现混沌运动状态。
| [1] | 陈兵奎, 易文翠, 钟晖, 等. 线面共轭啮合原理及齿面构建方法[J].机械工程学报, 2012, 48(19):17-22. CHEN Bingkui, YI Wencui, ZHONG Hui, et al. Theory of curve-surface conjugated and method of teeth surfaces constructed[J]. Journal of Mechanical Engineering, 2012, 48(19):17-22. (in Chinese)( 1) 1) |
| [2] | 王时龙, 祁鹏, 周杰, 等. 数控滚齿机热变形误差分析与补偿新方法[J].重庆大学学报, 2011, 34(3):13-17. WANG Shilong, QI Peng, ZHOU Jie, et al. Thermal deformation error analysis anf a novel compensation method for NC gear hobbing machine tools[J]. Journal of Chongqing University, 2011, 34(3):13-17. (in Chinese)( 1) 1) |
| [3] | Montestruc A N. Influence of planet pin stiffness on load sharing in planetary gear drives[J]. Journal of Mechanical Design, 2010, 133(1):788-796.( 1) 1) |
| [4] | CHEN Zaigang, SHAO Yimin. Mesh stiffness calculation of a spur gear pair with tooth profile modification and tooth root crack[J]. Mechanism and Machine Theory, 2013, 62:63-74.( 1) 1) |
| [5] | CHEN Zaigang, SHAO Yimin. Dynamic simulation of spur gear with tooth root crack propagating along tooth width and crack depth[J]. Engineering Failure Analysis, 2011,18(8):2149-2164.( 1) 1) |
| [6] | 李同杰, 朱如鹏, 鲍和云, 等. 行星齿轮系扭转非线性振动建模与运动分岔特性研究[J].机械工程学报, 2011, 47(21):76-83. LI Tongjie, ZHU Rupeng, BAO Heyun, et al. Nonlinear torsional vibration modeling and bifurcation characteristic study of a planetary gear train[J]. Journal of Mechanical Engineering, 2011, 47(21):76-83. (in Chinese)( 3) 3) |
| [7] | SUN Tao, HU Haiyan. Nonlinear Dynamics of a Planetary Gear System with Multiple Clearances[J]. Mechanism and Machine Theory, 2003, 38(12):1371-1390.( 1) 1) |
| [8] | 李同杰, 朱如鹏, 鲍和云, 等. 行星齿轮传动系的周期运动及其稳定性[J]. 振动工程学报, 2013,26(6):815-822. LI Tongjie, ZHU Rupeng, BAO Heyun, et al. Coexisting periodic solutions and their stability of a nonlinear planetary gear train[J]. Journal of Vibration Engineering, 2013, 26(6):815-822.(in Chinese)( 2) 2) |
| [9] | SHAO Yimin, CHEN Zaigang. Dynamic features of planetary gear set with tooth plasticinclination deformation due to tooth root crack[J]. Nonlinear Dynamics, 2013, 74(4):1253-1266.( 2) 2) |
| [10] | LI Tongjie, ZHU Rupeng, BAO Heyun. Study on dynamic load sharing behavior of two-stage planetary gear train based on a nonlinear vibration model[J]. Applied mechanics and Materials, 2011, 86:611-614.( 1) 1) |
| [11] | Parker R G, Wu X H.Vibration modes of planetary gears with unequally spaced planets and an elastic ring gear[J]. Journal of Sound and Vibration, 2010, 329(11):2265-2275.( 1) 1) |
| [12] | Singh A. Load sharing behavior in epicyclic gears:Physical explanation and generalized formulation[J]. Mechanism and Machine Theory, 2010, 45(3):511-530.( 1) 1) |
| [13] | 虞烈, 刘恒. 轴承转子系统动力学[M]. 西安:西安交通大学出版, 2001. YU Lie, LIU Heng. Dynamics of bearing-rotor system[M]. Xi'an:Xi'an Jiaotong University Press, 2001. (in Chinese)( 2) 2) |
| [14] | Han Qingkai. Periodic motion stability of a dual-disk rotor system with rub-impact at fixed limiter[J]. Vibro-Impact Dynamics of Ocean System and Related Problems, 2009, 44:105-109.( 2) 2) |
| [15] | 张家忠.非线性动力系统的运动稳定性、分岔理论及其应用[M].西安:西安交通大学出版社,2010. ZHANG Jiazhong.Motion stability, bifurcation theory and its application of nonlinear dynamical systems[M]. Xi'an:Xi'an Jiao Tong University Press, 2010. (in Chinese)( 5) 5) |
 2016, Vol. 39
2016, Vol. 39

