风电齿轮箱收缩盘是联接风电主轴和主齿轮箱低速级转架的主要部件,它所联接的两个部件转速较慢,但是扭矩比较大,并且载荷不稳定。为了使收缩盘联接具有足够的强度承担这种变化较大的载荷,必须对收缩盘联接进行强度计算和可靠性计算。
收缩盘联接可以归结为圆柱圆锥过盈联接。过盈联接具有结构简单、定心能力好、承载能力高,以及在冲击载荷下性能良好等优点,因此,在工程中使用广泛。传统的计算方法是建立在弹性力学基础上,把收缩盘内外环、行星架、主轴等效为厚壁圆筒模型,并等效为平面应力问题应用拉梅方程进行计算[1, 2, 3],一些学者在此基础上也做过很多的研究,如李伟建等[4]提出锥面过盈联接的一种工程计算方法。有些学者利用有限元计算方法结合工程理论计算进行深入研究,如唐亮[5]对圆柱和圆锥过盈联接进行了理论计算并提出优化算法;殷丹华等[6]推导了圆锥无键联接接触压力的解析公式,并利用有限元进行了对比计算。由于传统解析方法没有考虑到接触和收缩盘内外环锥度的影响,很难精确求解,而以上学者虽然利用有限元方法考虑了联接的非线性,但由于简化为平面应力问题进行计算,未考虑到工作扭矩的影响,也未考虑到尺寸公差、加工误差以及各计算参数的分散性带来的整体联接的可靠性问题。
文中在收缩盘设计时将其简化为轴对称问题并在ANSYS中建立非线性接触的参数化有限元模型,施加载荷和约束进而求得结构应力和应变值,考虑到收缩盘受到主轴扭矩作用,通过修改APDL命令对结构应力进行修正计算,并在此基础上考虑收缩盘结构多种设计参数的不确定性计算得到结构可靠性,为优化设计提供依据。
1 可靠性分析方法 1.1 可靠性设计机械可靠性设计又称为机械概率设计,它是将随机方法引入到机械产品设计中,以产品的失效和可靠性作为研究对象的一种设计方法。因为与机械产品可靠性有关的种种因素均表现出不同程度的非确定性,即随机性,因此,产品的可靠性是一项系统工程,即是由多项工程实施和保证才能够保证产品的可靠性。而可靠性设计中所涉及到的变量都会处理成满足一定概率分布的随机变量,变量之间可以通过概率函数进行多值转换[7]。
1.2 蒙特卡罗随机有限元法蒙特卡罗法又称随机抽样法,概率模拟法或统计试验法,是概率分析中最常用的传统方法,它能清楚地模拟实际问题的真实行为特征[8]。蒙特卡罗随机有限元法,就是把确定性有限元技术与蒙特卡罗法相结合进行随机结构分析的方法[9]。蒙特卡罗超拉丁采样模拟是一种具有记忆性的采样方法,它将随机变量的取值范围分成具有等概率的n个区间(n为采样数目),每一个随机变量在每一个区间中只能“撞击”一次,因此,不会出现采样点重叠的现象[10]。将这些随机样本值按有限元的建模、网格划分、求解的步骤进行计算,得到结构响应分析的结果变量数值。重复各变量随机取值、得到结果变量的n个数值,最后对结果变量进行统计,确定其各种统计参数如均值、方差、偏态系数、峰态系数等,以及概率分布函数等参数,为可靠性分析作好准备。
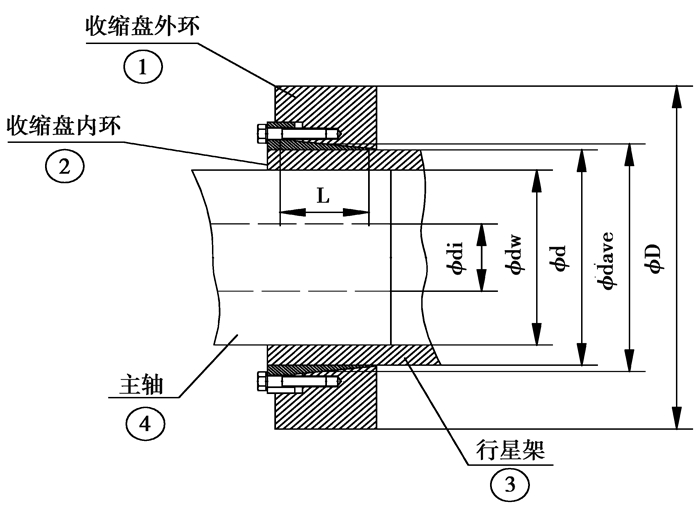
2 收缩盘联接有限元分析 2.1 收缩盘装配工作原理收缩盘联接结构件主要由收缩盘内环、外环、主轴和行星架构成,如图 1所示。
|
图1 收缩盘装配简图 Fig. 1 Shrink disc connection |
收缩盘内环外环为锥面配合,装配时通过拧紧内环螺栓产生轴向推力使得内外环紧密配合,产生沿锥面法向的压力,通过消除各接触面的间隙并产生摩擦力来传递主轴扭矩[11],因此,对于联接的传扭性能来说,各接触面摩擦力矩之和需大于主轴工作扭矩,否则在联接处将产生打滑并造成联接失效。同时,必须保证收缩盘内外环、转架和主轴结构件的强度以防止应力超过屈服极限而造成强度失效。
2.2 收缩盘联接有限元模型为简化计算提高后续可靠性的计算速度,需要对模型进行适当的简化。考虑到模型在不受扭矩作用下只承受径向和轴向载荷,其内部的应力状态为轴对称应力状态,因此,可以将模型简化成轴对称问题进行求解。在轴对称问题下,通过旋转体轴线的子午面在变形过程中始终不会扭曲,所以在θ面(周向)上没有剪应力。而实际工况中,收缩盘将承受主轴扭矩作用,因此,需要在原轴对称应力结果下修正θ面剪应力,应用Von Mises准则进行强度校核,为
| $\sigma =\sqrt{\frac{{{\left( {{\sigma }_{x}}-{{\sigma }_{y}} \right)}^{2}}+{{\left( {{\sigma }_{z}}-{{\sigma }_{y}} \right)}^{2}}+{{\left( {{\sigma }_{z}}-{{\sigma }_{x}} \right)}^{2}}+6\left( \tau _{xy}^{2}+\tau _{yz}^{2}+\tau _{xz}^{2} \right)}{2}},$ | (1) |
式中:σx、σy、σz、τxy分别从ANSYS结果数据库中提取;τyz和τxz都为周向切应力,其中τyz=0,τxz=$\frac{{{M}_{i}}{{\rho }_{i}}}{{{I}_{p}}}$,式中Mt为扭矩,ρi为第i个节点的回转半径,Ip为截面极惯性矩。
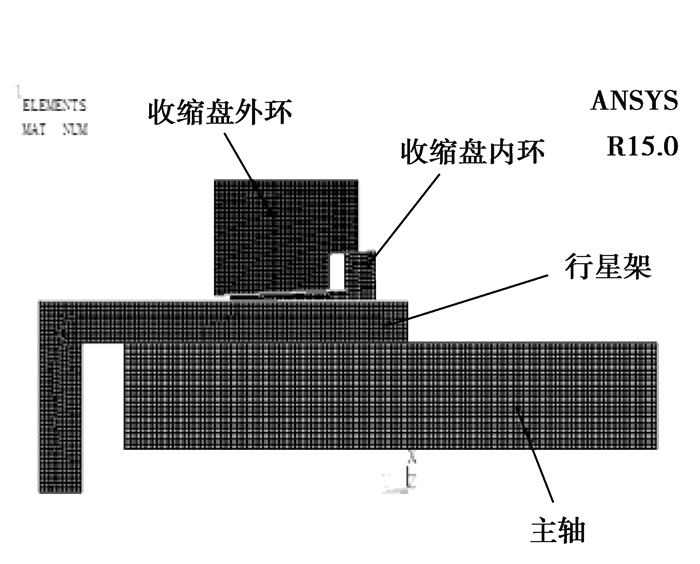
收缩盘联接有限元模型如图 2所示,结构件单元都为Plane182轴对称单元。行星架材料为QT700,其弹性模量为1.76×1 011 Pa,屈服强度为380 MPa,收缩盘内外环和主轴材料为42CrMoA,弹性模量为2.06×1 011 Pa,其中,收缩盘内外环热处理后屈服强度为1 200 MPa,主轴屈服强度为900 MPa。需要在收缩盘内外环之间、收缩盘内环和行星架之间以及行星架和主轴之间建立非线性接触,接触对单元采用Contac172和Target169单元进行模拟,摩擦系数为0.2,其中,需要考虑到行星架和主轴之间的过盈量0.069 mm。忽略螺栓联接,以内环轴向等效位移代替预紧作用,内环轴向推程为25 mm。主轴的工作扭矩为3 800 kN·m不直接施加在有限元模型上,但在后续切应力修正上体现出。
|
图2 收缩盘有限元计算模型 Fig. 2 FEA model of shrink disc connection |
收缩盘联接首先需要保证可传扭能力,即各接触面摩擦力矩合力应大于工作扭矩以保证接触面不打滑,这需要提取各接触单元上的接触压力计算出总的摩擦力矩Ttotal。在所有接触面中,主轴和行星架之间的接触为最重要的接触,传动链的动力主要通过这对接触从主轴传递到行星架上,它也是最为薄弱容易出现打滑的一对接触,因此,文中主要关注此处的联接可靠性,其Ttotal为
| ${{T}_{\text{total}}}=\sum\limits_{i=1}^{n}{\frac{{{p}_{i}}\pi {{D}^{2}}L\mu }{2}},$ | (2) |
式中:pi为每个接触单元法向接触应力;D为接触单元的回转直径;L为接触线长度;μ为摩擦系数;n为接触单元个数。
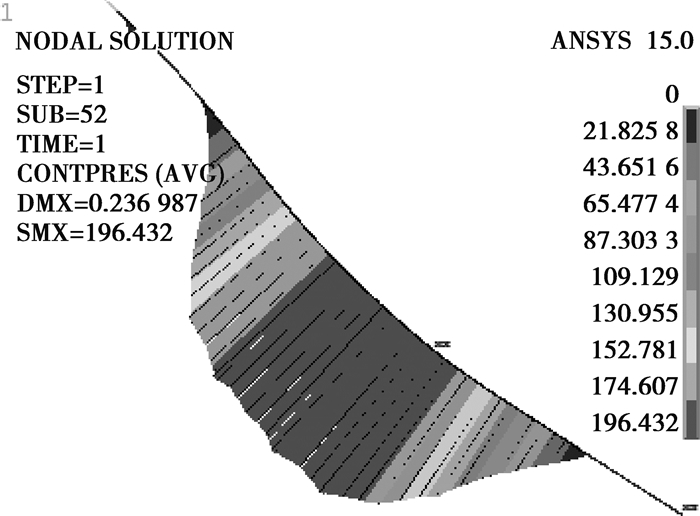
图 3为主轴和行星架之间接触面上的法向接触应力分布,可以看出在接触面中部应力分布比较均匀,最大接触应力为196 MPa。经过式(2)通过插入APDL命令在ANSYS后处理中得到Ttotal=5 118 kN·m,摩擦力矩大于工作力矩,联接可靠,主轴和行星架之间的接触不会发生打滑。
|
图3 主轴-行星架法向接触压力分布 Fig. 3 Pressure distribution between shaft and LSS |
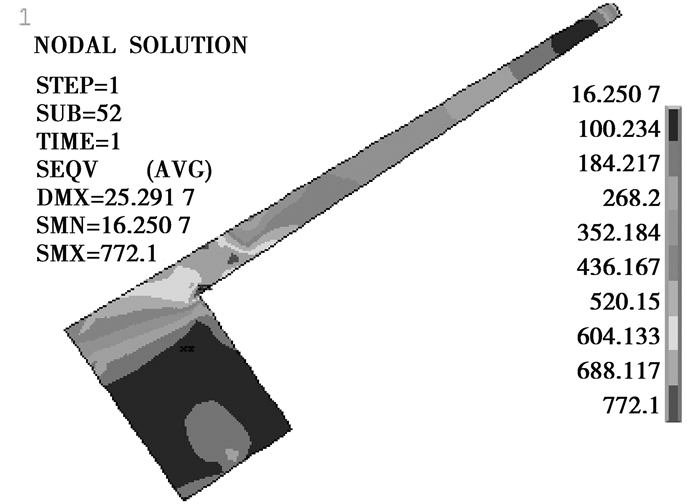
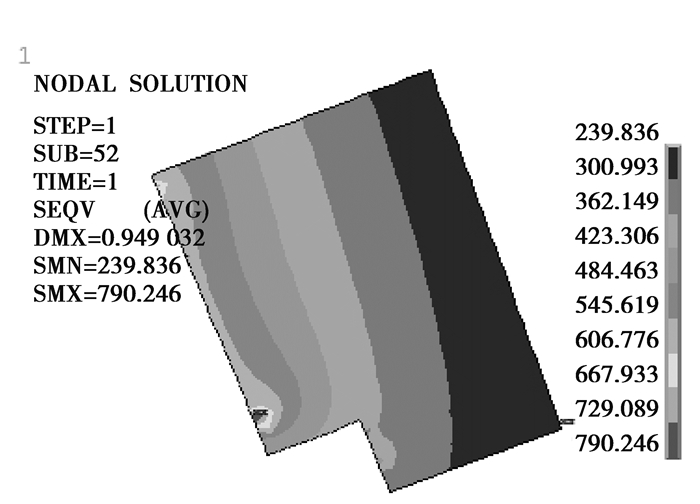
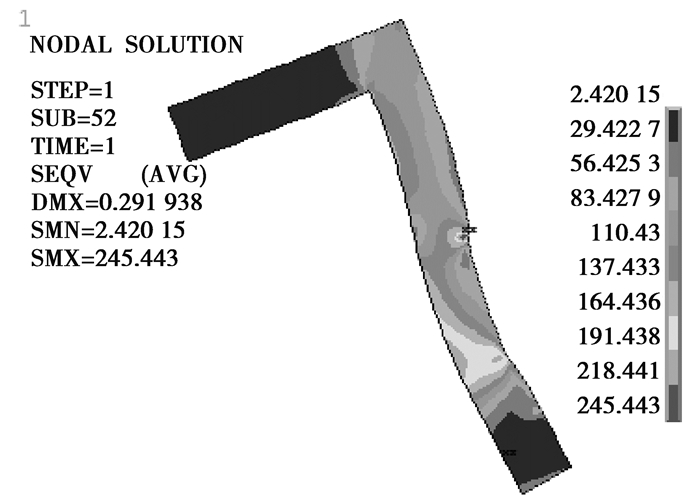
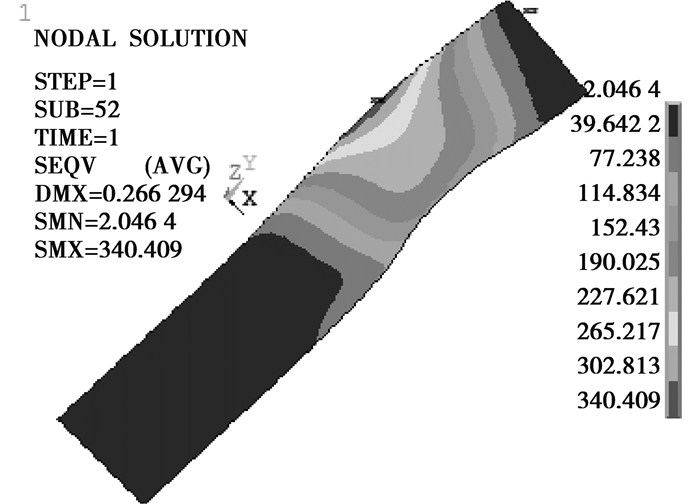
结构件强度分析主要关注到结构件的应力是否超过各自材料的屈服强度。ANSYS提取出未考虑到扭矩作用下的Von Mises应力,如图 4~7所示。其中,收缩盘内外环在接触区域应力较高,最大应力达到790 MPa,行星架在也在与收缩盘内环接触的边缘位置达到应力最大值245 MPa,主轴应力较为均匀,其最大应力为340 MPa。内外环局部应力过大是由于应力奇异造成,在后续可靠性分析中需要将此剔除。
|
图4 收缩盘内环米塞斯应力 Fig. 4 Von-mises stress of inner shrink disc |
|
图5 收缩盘外环米塞斯应力 Fig. 5 Von-mises stress of outer shrink disc |
|
图6 行星架米塞斯应力 Fig. 6 Von-mises stress of LSS |
|
图7 主轴米塞斯应力 Fig. 7 Von-mises stress of shaft |
考虑工作扭矩作用后,根据式1通过插入APDL命令对各结构件每个节点应力进行切应力修正,修正后结构件最大应力均小于各自屈服强度,结构件强度满足设计要求,如表 1所示。
| 表1 收缩盘计算最大应力结果 Table 1 The maximum stress of component |
概率设计技术是用来评估设计参数的不确定性对于系统响应的影响行为及其特性,其中,设计参数包括几何尺寸、加工误差、材料、载荷等不确定因素[12]。根据实际工作情况,以抽取主轴和行星架之间的接触面摩擦系数(MU1)、主轴和行星架接触过盈量(delta1)、收缩盘内外环半锥角(angle)、收缩盘内环小端高度(height_i)、收缩盘内环推程(distance)以及主轴工作扭矩(MX0)为满足一定分布的随机变量,设计参数如表 2所示。
| 表2 设计变量及其分布 Table 2 Design variable and distribution |
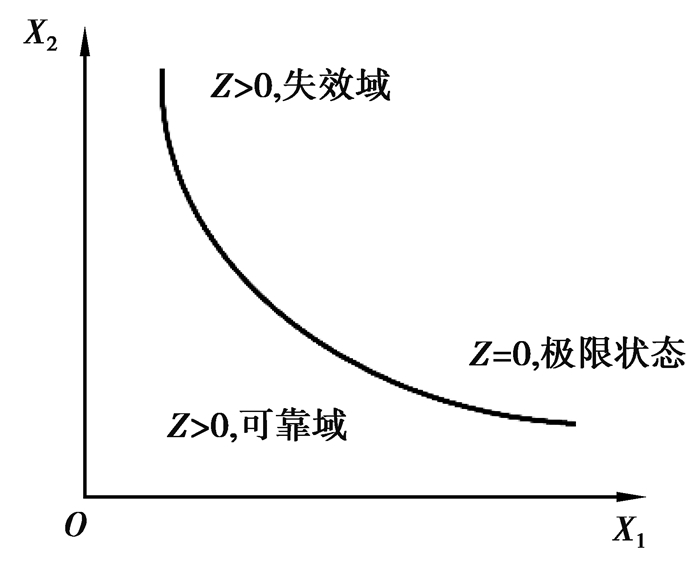
在整个系统,如果结构的一部分超过某一特定状态就不能满足设计规定的某一功能要求,该状态就称为结构极限状态。结构的极限状态实质上是结构工作状态的一个阀值[13],如果工作状态超过这一阀值,则结构处于不安全、不耐久或不适用的状态;若工作状态没超过这一阀值,则结构处于安全、耐久、适用的状态。一般用Z=g(X)表示结构的工作状态,称作结构的功能函数。当Z>0时结构可靠,当Z < 0时结构失效,当Z=0时,结构处于极限临界状态[14],如图 8所示。
|
图8 结构工作状态简图 Fig. 8 Structure function state |
功能函数Z=g(X)的累积分布函数F(X)为
| $F\left( X \right)=P\left( X\le x \right)=\int_{-\infty }^{x}{g\left( x \right)\text{d}x}。$ | (3) |
在实际工程中,结构失效的形式有很多种,只考虑结构单失效模式下的可靠度是不准确的。在本研究中,收缩盘联接的可靠性至少包括了联接可靠性和结构强度可靠性,该串联模式中任一结构失效则会造成整体结构的失效[15]。一般由于主轴、收缩盘内外环材料较好、强度较高,很少发生屈服,而行星架在整个系统中偏危险,因此,在结构强度可靠性分析中只考虑行星架以减少计算量。
定义Z1=Ttotal-MX0为联接功能函数,当Ttotle < MX0时,Z1 < 0联接失效;
定义Z2=σallowable-σ为结构件强度功能函数,σallowable为行星架屈服强度,σ为行星架修正剪应力后的米塞斯应力,当Z2 < 0时结构件强度失效;
定义Z01为Z1和Z2串联系统的功能函数,显然当Z1或Z2任意一值小于零时,Z01 < 0,因此,Z01可表示为
| ${{Z}_{01}}=\left\{ \begin{align} & -{{Z}_{1}}\times {{Z}_{2}}\ \ \ \left( {{Z}_{1}} < 0并且{{Z}_{2}} < 0 \right), \\ & {{Z}_{1}}\times {{Z}_{2}}\ \ \ \ \ \ \ \ \ \ \ \ \ \left( 其他 \right)。 \\ \end{align} \right.$ | (4) |
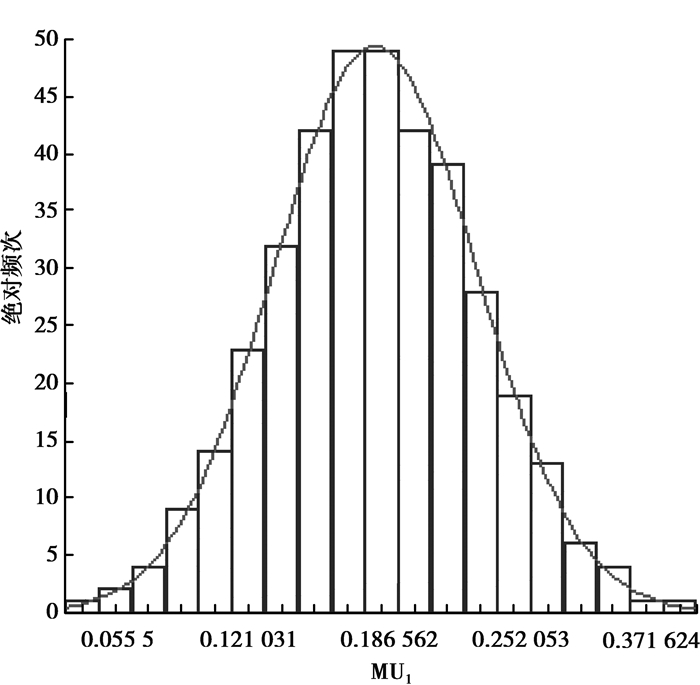
在ANSYS/PDS模块下,采用Monte Carlo超拉丁方抽样法对模型参数进行380次抽样计算,对各参数的样本进行检查,随着采样次数的增加各样本基本上都满足各自分布函数,采样均值和采样方差都收敛于各自分布设定的均值和方差,说明样本抽样有效,样本点数目也达到统计要求。从图 9可以看出摩擦系数(MU1)的采样频率基本上满足正太分布函数。图 10显示的是推程(distance)的采样频率分布,基本上也满足均匀分布,均值稳定在27.5左右。
|
图9 摩擦系数(MU1)的采样频率分布 Fig. 9 The distribution of MU1 sampling |

|
图10 推程(distance)的采样分布 Fig. 10 The distribution of distance sampling |
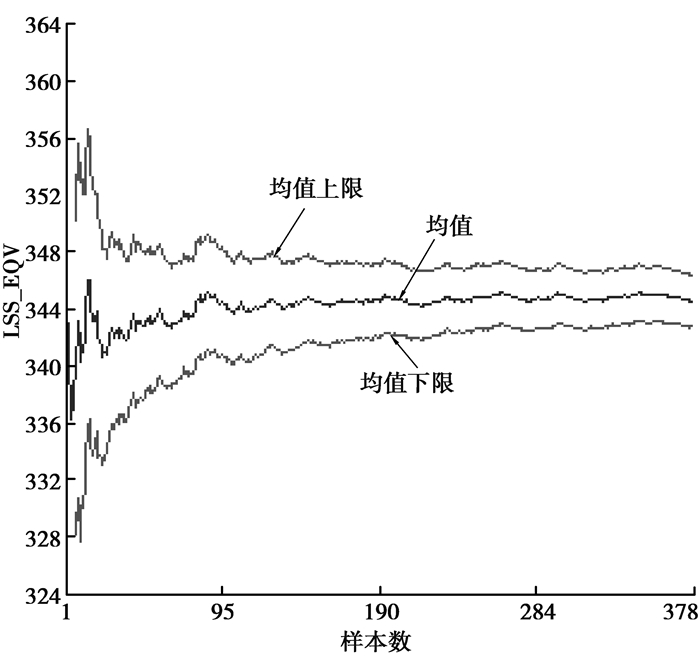
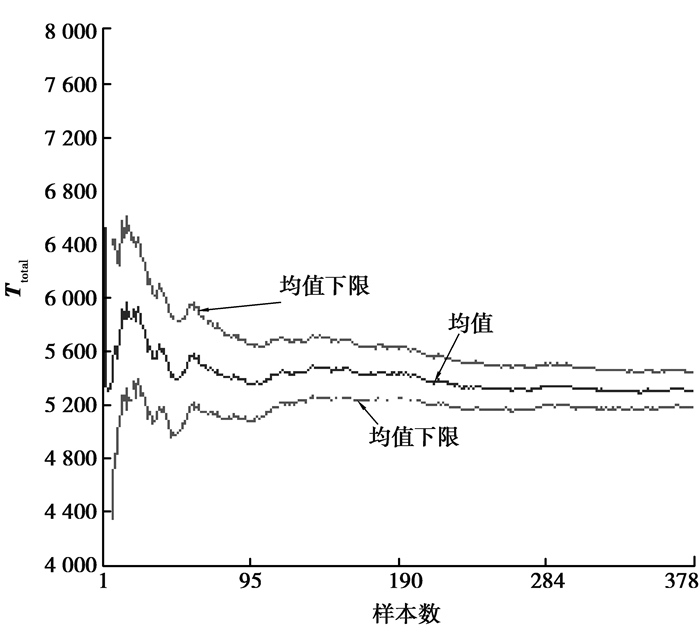
对于结果评判,主要输出了行星架修正后的等效应力(LSS_EQV)和接触面合成的摩擦力矩(Ttotle)。从图 11为等效应力LSS_EQV在95%置信空间下的均值走势,经过多次采样计算后等效应力均值收敛在344 MPa左右,低于其屈服强度380 MPa。图 12为摩擦力矩Ttotle在95%置信空间下的均值走势,随着抽样计算次数的增加,置信区间的宽度不断减小,均值收敛在5 400 kN·m左右,高于主轴工作扭矩3 800 kN·m。
|
图11 等效应力(LSS_EQV)均值走势 Fig. 11 The convergence of LSS_EQV |
|
图12 摩擦力矩(Ttotle)均值走势 Fig. 12 The convergence of Ttotle |
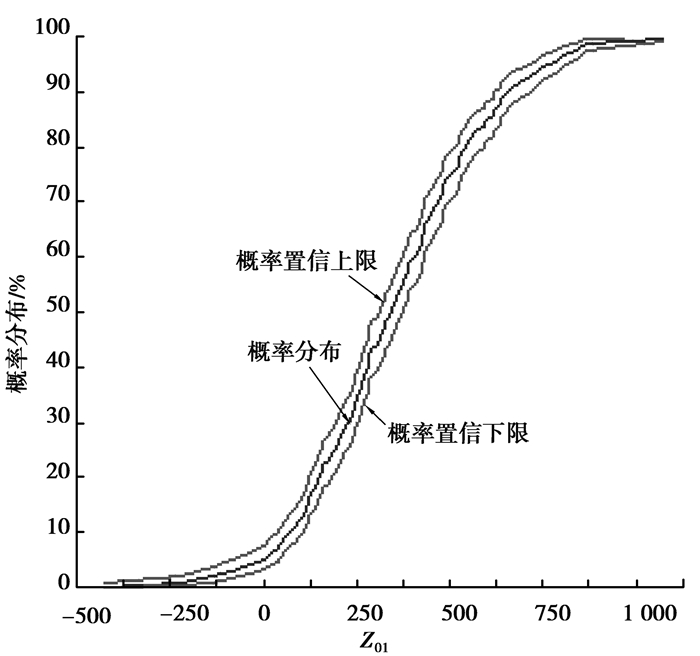
图 13为总体功能函数Z01的累积概率分布图,可以看出,在95%的置信度下Z01 < 0的概率为5.2%,即系统整体的可靠度为94.8%,失效率为5.2%,可靠度相对较高满足了设计的要求。
|
图13 Z01累积概率分布 Fig. 13 Cumulative distribution function of Z01 |
图 14为Z01的灵敏度示意图,可以看出摩擦系数、推程和收缩盘内环小端面高度对整体功能函数影响较大。其中,摩擦系数的大小对联接的传扭性能有较大影响,摩擦系数越大传扭性能越好。收缩盘内环的推程大小对传扭性能和结构件强度有较大影响,推程越大收缩盘接触面挤压力就越大从而传扭性能和结构件应力越高。而收缩盘小端面的高度的改变则会影响行星架局部的应力大小。其他参数对功能函数影响则很小,因此在设计时可以根据需要把握主要参数。

|
图14 Z01敏感度示意 Fig. 14 The sensitivities of Z01 |
1) 通过对风电齿轮箱收缩盘强度进行分析,结果表明收缩盘联接的各结构件强度满足设计要求,接触面未发生打滑,传扭性能有效。
2) 应用ANSYS/PDS模块对收缩盘联接进行可靠性分析,可以看出整体可靠度为94.8%,其中接触面的摩擦系数、收缩盘内环推程值和其小端面高度值对整体可靠度均有较大的影响。
3) 通过使用有限元法大大提高了分析的精度,缩短了设计周期并有效的对产品进行优化提高经济效益。
| [1] | 徐芝纶.弹性力学简明教程[M].北京:高等教育出版社,2002. XU Zhilun.Introduction to elasticity[M].Beijing:Higher Education Press, 2002.(in Chinese)( 1) 1) |
| [2] | 林绍邦.圆锥面过盈联接[J].广东机械学院学报,1994,12(1):23-29. LIN Shaobang.Interference-couple technology between cone surfaces[J].Journal of Guangdong Mechanical Institute,1994,12(1):23-29.(in Chinese)( 1) 1) |
| [3] | 魏延刚.轴毂过盈联接的应力分析和接触边缘效应[J].机械设计,2004,21(1):36-39. WEI Yangang.Research on stress analysis and contacting edge effect for interference fit joint of hub[J].Journal of Machine Design,2004,21(1):36-39.(in Chinese)( 1) 1) |
| [4] | 李伟建,潘存云.锥面过盈联接静力分析的一种工程方法[J].机械强度,2011,33(1):86-92. LI Weijian,PAN Cunyun.Engineering approach to static analysis of tapered interference fit[J].Journal of Mechanical Strength,2011,33(1):86-92.(in Chinese)( 1) 1) |
| [5] | 唐亮.风电锁紧盘的算法优化与分析研究[D].太原:太原科技大学,2014. TANG Liang.The algorithm optimization and research on wind turbine's shrink disk[D].Taiyuan:Taiyuan University of Science & Technology,2014.(in Chinese)( 1) 1) |
| [6] | 殷丹华,朱如鹏.一种圆锥面无键联接接触压力和应力的解析计算方法[J].中国制造业信息化,2011,40(11):22-25. YIN Danhua,ZHU Rupeng.A calculation for the contact pressure and stress of conical keyless connection[J].Manufacturing Information Engineering of China,2011,40(11):22-25.(in Chinese)( 1) 1) |
| [7] | 冯桢,于涛,郭培燕,等.基于ANSYS/PDS模块的油缸可靠性设计[J].煤矿机械,2006,27(11):21-23. FENG Zhen,YU Tao,GUO Peiyan,et al.Probabilistic design of cylinder using ansys/pds[J].Coal Mine Machinery,2006,27(11):21-23.(in Chinese)( 1) 1) |
| [8] | 董艳秋,田敬博.蒙特卡洛法结构可靠性分析[J].黑龙江工程学院学(自然科学版),2010,24(1):27-29. DONG Yanqiu,TIAN Jingbo.Structural reliability analysis of Monte Carlo method[J].Journal of Heilongjiang Institute of Technology,2010,24(1):27-29.(in Chinese)( 1) 1) |
| [9] | 李良巧.机械可靠性设计与分析[M].北京:国防工业出版社,1998:67-76. LI Liangqiao.Mechanical reliability design and analysis[M].Beijing:National Defense Industry Press,1998:67-76.(in Chinese)( 1) 1) |
| [10] | 曾攀,雷丽萍,方刚.基于ANSYS平台有限元分析手册——结构的建模与分析[M].北京:机械工业出版社,2011. ZENG Pan,LEI Liping,FANG Gang.Finite element analysis guide:modeling and analysis of structure[M].Beijing:China Machine Press,2011.(in Chinese)( 1) 1) |
| [11] | 杜静,程海燕,何玉林,等.风力发电机组主轴胀套联接有限元分析[J].机械与电子,2009(1):68-70. DU Jin,CHEN Haiyan,HE Yulin,et al.Finite element analysis of taper-lock connection in wind turbine spindle[J].Mechanical and Electronic,2009(1):68-70.(in Chinese)( 1) 1) |
| [12] | 王建梅,陶德峰,唐亮,等.加工偏差对风电锁紧盘性能的影响分析[J].机械设计,2014(1):59-63. WANG Jianmei,TAO Defeng,TANG Liang,et al.Analysis of influence on performance of wind turbine's shrink disk by machining deviation[J].Journal of Machine Design,2014(1):59-63.(in Chinese)( 1) 1) |
| [13] | 刘成立.复杂结构可靠性分析及设计研究[D].西安:西北工业大学,2006. LIU Chengli.Research on reliability analysis and design of complex structure[D].Xi'an:Northwestern Polytechnical University,2006.(in Chinese)( 1) 1) |
| [14] | ANSYS 15.0高级分析指南[M].ANSYS Inc, 2013. ANSYS 15.0 a dvanced analysis guide[M]. ANSYS, Inc, 2013.( 1) 1) |
| [15] | 熊会民,卢玉明.机械串联系统的可靠性[J].中国科学技术大学学报,1990(1):116-121. XIONG Huimin LU Yuming.A reliability of mechanical series system[J].Journal of China University of Science and Technology,1990(1):116-121.(in Chinese)( 1) 1) |
 2016, Vol. 39
2016, Vol. 39

