2. 中国科学院武汉岩土力学研究所 岩土力学与工程国家重点实验室, 武汉 430071;
3. 河南理工大学 土木工程学院, 河南 焦作 454003
2. State Key Laboratory of Geomechanics and Geotechnical Engineering, Institute of Rock and Soil Mechanics, Chinese Academy of Sciences, Wuhan 430071, P. R. China;
3. School of Civil Engineering, Henan Polytechaic University, Jiaozuo 454003, Henan, P. R. China
随着国内矿物冶炼技术的不断进步,矿山尾矿颗粒呈现细粒化的发展趋势。由于目前对细粒尾矿的定义还没有达成普遍共识,笔者将颗粒粒径大于0.075 mm的质量占土粒总质量的50%以下的尾矿视为细粒尾矿。同传统工艺产生的尾矿不同,新型细粒化工艺下的尾矿颗粒粒径均值更小,级配范围更窄,固结时间更长,筑坝静、动力稳定性也相对较差。研究细粒尾矿性质成为尾矿坝研究所遇到的新问题、新考验,围绕细粒尾矿问题开展理论研究具有很强的现实指导意义和学术价值。
尾矿是一种结构性人造多分散粉体,它的粒径分布既十分复杂,又有一定规律。一方面,尾矿筑坝是一个大规模、长时期的过程,在此期间粉碎工艺的改进、沉积距离的改变等,都会影响颗粒粒径分布,在坝体内形成复杂的级配空间分布;另一方面,细粒尾矿的形成和搬运过程受人工控制,产生的颗粒群的级配具有一定的规律性。细粒尾矿的粒径分布是一个受多因素控制的问题,影响着尾矿的物理力学特性,研究细粒尾矿的粒径分布规律,可为细粒尾矿的土工试验提供更为科学的级配方案,也是确定坝体破坏模式的依据。
如果某种颗粒群的粒度分布符合某种数学规律,则可以用粒度分布数学模型来描述粒度分布[1]。A.M.Gaudin在1926年基于大量磨矿实验得到的粒度分布函数为
| $F\left( x \right)=c{{x}^{a}},$ | (1) |
式中:F(x)为分布函数;x为粒度大小;a、c为实验参数。
Rosin等[2]于1933年提出可以用二参数的Weibull分布函数描述粉煤灰的粒径分布。Weibull[3]在1951年详细总结了二参数的Weibull分布函数的各种应用实例。Jopony等[4]分析了马来西亚Lohan地区铜矿粒径分布的函数表达式。Giuliano V等[5]对硫铁尾矿水系沉积物的粒度进行干、湿筛分和激光粒度分析,发现硫铁尾矿沉积物的分布可以用Rosin-Rammler函数描述。Gonzales等[6]研究了不同粒度分布的尾矿材料在空气中的扩散范围及其对环境影响。郑钢镖等[7]利用粒径的密度分布函数求取了任意两个分布粒径之间粉尘重量所占总粉尘重量的百分比。刘铁英等[8]拟合单、双峰的颗粒尺寸分布,取得良好的反演效果。李功伯等[9]探讨了微观尺度上矿石破碎过程,并认为其符合G-S分布函数。以上对散体材料颗粒粒径分布的研究为探讨细粒尾矿材料粒径分布规律奠定了良好基础,但从已有研究成果可以看出,不同的粉体具有不同的粒径分布,针对细粒尾矿粒径分布的数学模型研究较少,对模型的分析和应用还鲜有提及。
粒径分布的自相似特性在很早就引起了人们的注意,对破碎块石粒径分布的分形描述取得了巨大成功。Mandelbrot[10]早在1983就用分形方法对破碎矸石块度分布进行研究,发现其具有高度的自相似特点。高峰等[11]认为G-S分布函数和Weibull分布函数都可以归结为分形分布。杨金玲等[12]发现实验所得的体积分形维数比质量分形维数小是由实验方法不同导致的。胡云锋等[13]针对不同土地利用条件下土壤粒径分布的分维特征进行统计,结果表明风蚀强度越大,土壤分维越小。张季如等[14]通过对6种土样的偏光显微镜观察,提出用数量分布表征土壤分形特性。目前,针对细粒尾矿粒度分形的研究成果不多,分形维数描述和数学模型描述的优劣还缺乏例证。
在粒径分布形成机理方面,许多学者也进行过研究。Epstein[15]将岩石破碎的过程看作是多次破碎的效果叠加,每次破碎的效果可以由两个函数进行控制。李功伯等[9]把矿岩粉碎的过程假设为一个四面体的四角不断地被分割的自相似模型,并推导了粒径分布的分形函数。谢和平等[16]从岩石的损伤演化的角度分析岩石的破损问题,认为粒径分布的自相似是由于微观裂隙几何形状的自相似引起的。由于粒径分布控制因素复杂,一种粉体粒径分布的产生机理并不一定适用于所有粉体,这就要求具体问题具体分析,在引用前人结论时留意研究成果的适用性。
从已有资料上看,目前国内还缺乏针对细粒尾矿粒径分布的研究,这导致的最主要问题是:
1) 在配制实验级配时,用筛分后的各级粒径进行配比,配比出的级配不符合自然条件下的级配规律,降低了研究价值和结论可靠性;
2) 工程上常用D50、Cu、Cc值描述级配,但这种方法实质上是用级配曲线上的特殊点来代表整体曲线,无法反映粒径分布曲线所包含的全部信息。
笔者以甘肃某铅锌矿尾矿库试样为研究对象,验证了二参数Weibull分布函数对细粒尾矿粒径分布描述的准确性,阐述了该分布函数在工程上的应用,并将其与分形描述进行对比,最后给出了一种粒径分布形成过程的机理解释。
1 细粒尾矿粒径分布模型的建立 1.1 试样描述及粒度分析试验结果本次试验样本包括82个标准尾矿试样,取自甘肃某铅锌尾矿库库区轴线上布置的5个具有代表性的钻孔,钻孔编号为zk22、zk23、zk24、zk25与zk26,具体的位置见图 1所示。其中,zk22与zk23位于初期坝,zk24、zk25与zk26布置于堆积子坝。本次取样钻孔深度在46~94 m之间,取样间隔随深度变化:0~20 m内,每2.0 m取一个样;20~30 m内,每2.5 m取一个样;30~50 m内,每3.0 m取一个样;50 m往下,每4.0 m取一个样。将试样用铁皮包裹、密封、编号后,运输至实验室分析。
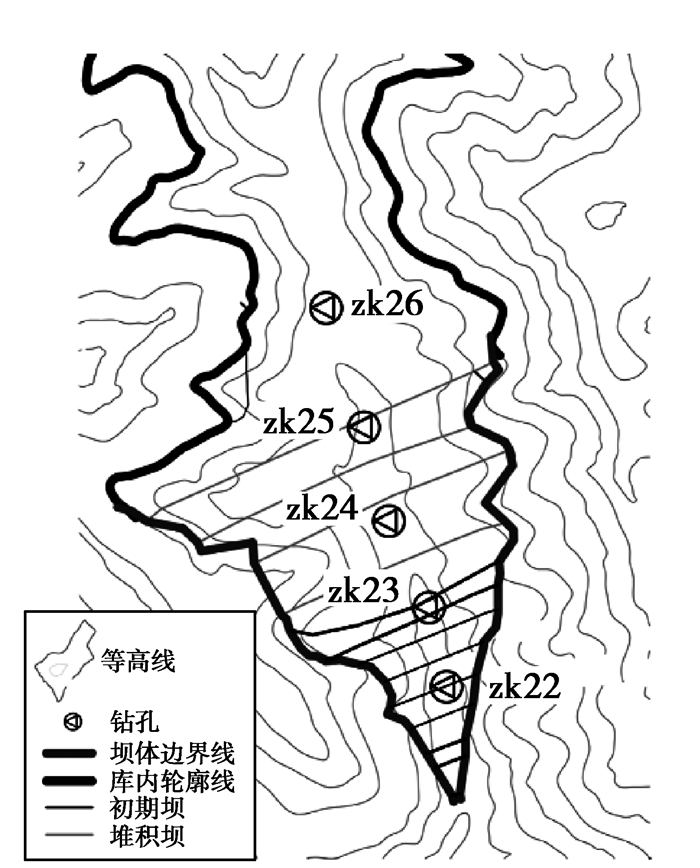
|
图1 钻孔布置平面图 Fig. 1 Floorplan of drill hole |
对大于0.075 mm的土粒用筛分法分析,对小于0.075 mm的土粒用密度计法分析,并绘制筛下积累分布曲线,图 2是一个典型的尾矿试样粒度特性指标试验结果。对试验结果统计发现,82个试样中,D50平均值0.039 mm,超过0.075 mm的试样共3个,约占总试样数的4%;D60均值0.051 2 mm,超过0.075 mm的试样共12个,约占总体的12%;D70均值0.067 mm,超过0.075 mm的试样共17个,约占总体的21%。从以上指标看,这些尾矿试样符合细粒尾矿的定义。
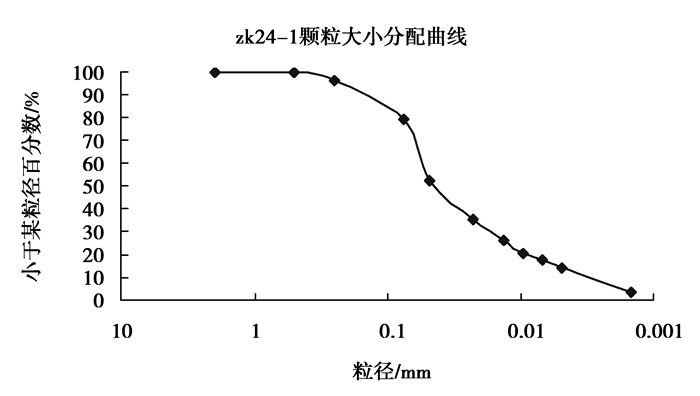
|
图2 粒度特性指标试验结果 Fig. 2 A typical cumulative particle-size distribution curve |
对土的粒径分布特征进行描述时,常采用平均粒径D50、不均匀系数Cu和曲率系数Cc。统计82个试样的颗分结果,平均粒径D50在0~0.1 mm之间,不均匀系数Cu大于5的试样大约占90%,曲率系数Cc介于1~3之间的占85%左右。
1.2 不同分布函数模型的准确性对比选用3种较常用的分布函数模型对细粒尾矿粒径分布进行对比。这3种分布函数分别为:二参数的Weibull分布函数、G-S分布函数和对数正态分布函数。
二参数的Weibull分布函数表达式为
| $F\left( x \right)=1-{{\text{e}}^{-\left( \frac{x}{\eta } \right)m}},$ | (2) |
式中:m为均匀性系数;η为特征粒径。
G-S分布函数表达式为
| $F\left( x \right)={{\left( \frac{x}{d} \right)}^{b}},$ | (3) |
式中:x为粒度大小;d为分布特征值;b为分布指数。
对数正态分布函数表达式为
| $F\left( x \right)=\frac{1}{2}\text{erfc}\left[ -\frac{\ln x-\mu }{\sigma \sqrt{2}} \right],$ | (4) |
式中:erfc为互补误差函数;μ为变量对数的平均值;σ为变量对数的标准差。
为了使得得到的积累分布曲线图像简单明了,方便对不同分布函数拟合结果进行对比,对函数进行线性化处理。对于式(2),经两次对等式两边取对数后,可得
| $lnln\frac{1}{1-F\left( x \right)}=m\ln x-m\ln \eta ,$ | (5) |
| $Y=lnln\frac{1}{1-F\left( x \right)},X=\ln x.$ | (6) |
则
| $Y=mX-m\ln \eta .$ | (7) |
同理,对于式(3),令
| $Y'=\ln F\left( x \right),X'=\ln x,$ | (8) |
那么,式(3)等价于
| $Y'=bX'-b\ln d.$ | (9) |
已知若x服从对数正态分布,则X″=lnx服从正态分布,即
| $\frac{X''-\mu }{\sigma }\tilde{\ }N\left( 0,1 \right).$ | (10) |
令
| $Y''=\frac{X''-\mu }{\sigma }\tilde{\ }N\left( 0,1 \right),$ | (11) |
则有Y″与X″呈线性关系,且服从标准正态分布N(0,1)。
将zk24-1号试样数据分布放在X-Y坐标、X′-Y′坐标和X″-Y″坐标下,并用最小二乘法进行拟合,结果如图 3所示。
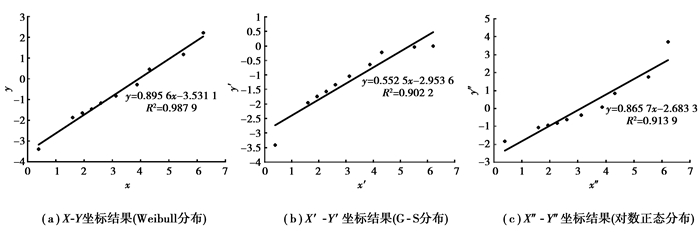
|
图3 3种分布函数拟合效果对比 Fig. 3 Fitting effect comparison of three kinds of functions |
从图 3看出,Weibull分布函数的可决系数约为0.98,G-S函数的可决系数约为0.90,对数正态分布函数的可决系数约为0.91,拟合效果最好的是Weibull分布函数。
为进一步检验结果可靠性,用同样的方式对24号钻孔的20个试样进行平行处理,去掉2个明显离散的试样结果,统计结果如表 1所示,Weibull分布函数的可决系数平均值约0.99,G-S函数和对数正态分布函数的可决系数平均值约为0.92,Weibull分布函数的拟合结果明显优于其他两个函数。
| 表1 3种分布函数拟合效果统计 Table 1 Comparison of three kinds of functions |
为了对试验数据在X-Y坐标中的线性相关性进行验证,本节选择24号钻孔数据中的zk24-19号数据进行计算证明。
用t检验法检验时,设统计假设为:
H0表示Y与X线性无关,H1表示Y与X线性相关。则拒绝域为
| ${{K}_{0}}=\left\{ \left| R \right|>{{r}_{a}}\left( n-2 \right) \right\},$ |
式中:rα(n-2)可从相关系数检验临界值表查得,这里取值0.872。
zk24-19号数据的相关系数R=0.984>0.872,故拒绝H0,认为Y与X线性相关。
同理,对表 1中的18个测试数据进行检验,结果均证明线性相关。
为进一步增加数据可靠性,对82个试样的拟合效果用可决系数进行统计,结果如表 2所示。
| 表2 Weibull分布函数拟合效果统计 Table 2 Fitting effect of Weibull distribution function |
从表 2可以看出,有75%以上的样本用Weibull分布函数拟合的可决系数大于0.98,92%以上的样本用Weibull分布函数拟合的可决系数大于0.95。这从统计上说明细粒尾矿的粒径分布是服从Weibull分布的。
2 Weibull粒径分布模型的应用 2.1 对粒径积累分布曲线的外推预测实验室中通常用筛分法和沉降法结合起来测量细粒尾矿的粒径分布,两者互有优劣。筛分法用时短,操作简单,但对细粒尾矿的筛分效果不理想;沉降法对细小颗粒的粒径有较好的辨析效果,但耗时长,操作复杂。由于细粒尾矿的粒径分布服从Weibull分布,因此,通过筛分法试验数据来预测沉降法的结果在理论上是可行的。
拟合曲线/直线对两端数据之间的内插预测较为可靠,但对超过两端数据点的外推预测则需要用试验进行检验。依据82次颗粒分析试验的结果可知,当细粒尾矿的粒径在0.001~0.500 mm之间时,Y与X满足线性分布关系,即当粒径在0.001~0.500 mm之间时,对粒径积累分布曲线的内推预测和外推预测都是可靠的。对于一元线性回归直线,置信度为95%的点预测区间为
| $\left( {{{\hat{Y}}}_{0}}-\delta \left( X{{Y}_{0}} \right),{{{\hat{Y}}}_{0}}+\delta \left( {{X}_{0}} \right) \right),$ | (12) |
式中: ${{\hat{Y}}_{0}}$ 为X=X0时的点预测值;δ(X0)为X=X0时的随机误差。
工程上往往需要的不是对某点的预测,而是对整个粒径分布函数的区域带预测。则X-Y关系的近似预测带公式为
| ${{{\hat{Y}}}_{1}}\left( X \right)=mX-m\ln \eta -{{u}_{1-\frac{a}{2}}}\hat{\sigma },$ | (13) |
| ${{{\hat{Y}}}_{2}}\left( X \right)=mX-m\ln \eta -{{u}_{1-\frac{a}{2}}}\hat{\sigma }.$ | (14) |
式中: ${{\hat{Y}}_{1}}$ (X)、 ${{\hat{Y}}_{2}}$ (X)为预测带上下边界函数;u为正态分布分位数;α为显著水平; $\hat{\sigma }$ 为残差标准差。
仍然以zk24-1号数据为例,其细筛筛分结果如表 3所示。
| 表3 zk24-1号试样细筛筛分结果 Table 3 zk24-1 sample sieve screening results |
根据表 3中实验结果,在X-Y坐标下做出的显著水平为0.05的预测带如图 4。从图 4可以看出,用3个数据点做出的最小二乘法外推拟合直线和图 3(a)中的拟合直线表达式相近,实测的9个数据点均落在预测带之内,对粒径积累分布曲线的外推预测是准确的。
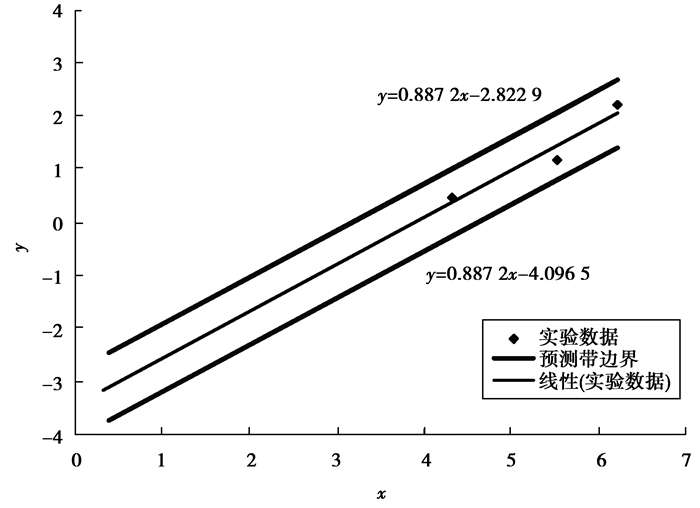
|
图4 据细筛筛分结果做出的XY拟合直线及其预测带 Fig. 4 Fitting line and its prediction belt in the X-Y coordinates |
将外推预测结果表达为粒径积累质量百分比关系,如图 5、表 4。可见,除了0.05 mm粒径附近的预测效果较差以外,其余粒径预测值与实测值基本吻合。
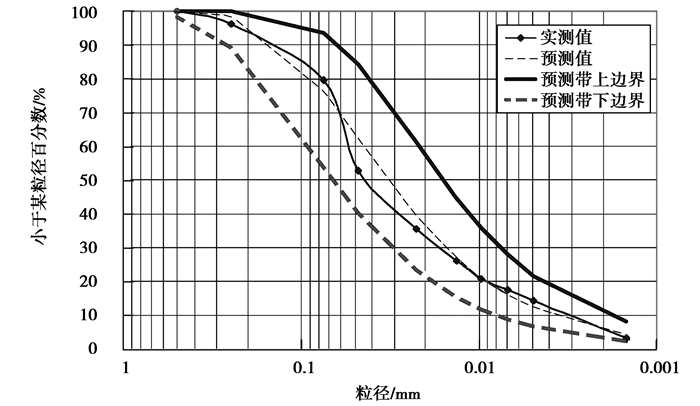
|
图5 外插法预测效果 Fig. 5 Extrapolation prediction effect |
| 表4 外插法预测效果 Table 4 Extrapolation prediction |
需要注意的是,本次外插只使用了3个点的数据,实际运用中可以在0.5~0.075 mm之间进行加密筛分,或者增加比0.075 mm更小孔径的筛子,点预测值定将更加贴近实测值,预测带也会更加狭小和准确。
2.2 对粒径分布概率密度函数的估计由于测量数据点的粒径不是等距间隔的,所以通过细粒尾矿的粒径的积累分布曲线不能直接获得概率密度曲线。例如用表 4中的数据作直方图时,其横坐标间距先密后疏,最小横坐标间距是3.44 μm,最大横坐标间距是250.00 μm,不能满足直方图分析要求。一种解决办法是,首先得到Weibull积累分布的函数表达式,计算得到m、η值,再根据Weibull概率密度函数对粒径的概率密度曲线进行估计。
二参数的Weibull概率密度函数表达式如下
| $f\left( x \right)=\frac{m}{{{\eta }^{m}}}{{x}^{m-1}}{{\text{e}}^{-\left( \frac{x}{\eta } \right)m}}.$ | (15) |
利用最小二乘法对表 4中数据进行计算可以得到zk24-1号试样的m=0.895 6,η=23.628 5,据此作出概率密度函数如图 6所示。从图可以看出,在细粒尾矿中,粒径细的颗粒所占比例高,粒径粗的颗粒所占比例低。这是因为矿石在粉碎为细粒尾矿的过程中,粗颗粒大量粉碎为细颗粒,而颗粒越细越不易粉碎,所以在最终粒径分布中颗粒越粗所占比例越低。
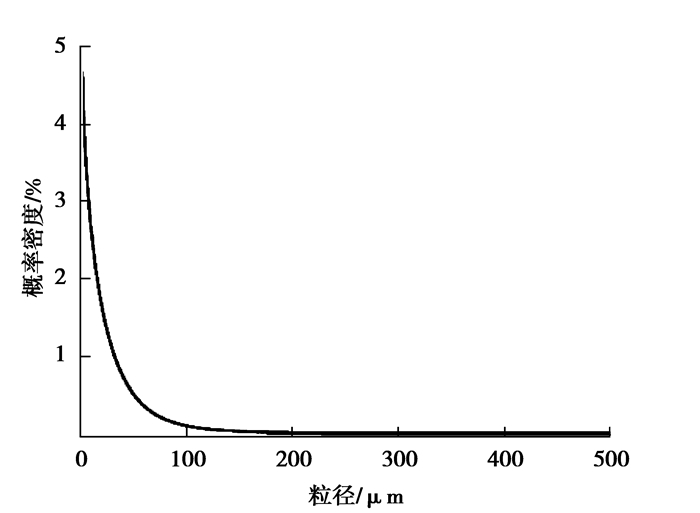
|
图6 对粒径分布概率密度函数的估计 Fig.6 Estimate of the particle size distribution of probability density function |
在解读Weibull分布模型的积累分布函数曲线和概率密度函数曲线时,必须结合实际情况对曲线两端的数据进行修正。从式(2)得到,只有当x=0和∞时,F(x)的值才能取到0和1。图 6结果也表明:当粒径无限增大时,概率密度无限接近于0,但并不等于0;当粒径无限接近于0时,概率密度取得最大值——而事实上,试样中没有大于0.5 mm粒径的颗粒,粒径小到某种程度时概率密度应该为0。
因此,在实际运用中需要对F(x)和f(x)加一些限制条件。对于图 6所示的曲线函数,可以认为粒径小于500 μm且大于1.5 μm时,Weibull分布模型对粒径的分布描述是准确的。
2.3 对大量级配数据的统计性描述级配指标是用来反映级配特征的物理量,但是现有描述指标不便于描述大量级配数据的统计性特征,为此,本节对颗分曲线进行分析,提出用2个指标描述颗分曲线的方法。
因为细粒尾矿的颗分曲线能够在XY坐标上形成一条直线,所以可以用直线的斜率和截距来描述粒径分布,即用均匀性系数m和比例参数B(定义B=-mlnη)唯一确定一条颗粒分布积累曲线。
B值控制级配的范围。取m=0.9,在B=-3.5、-4.0、-4.5、-5.0、-5.5、-6.0、-6.5、-7.0时绘制出相应的累积质量百分比与粒径关系见图 7,可知,随着B的减小,曲线向右移动,级配范围增大,粗颗粒增多。
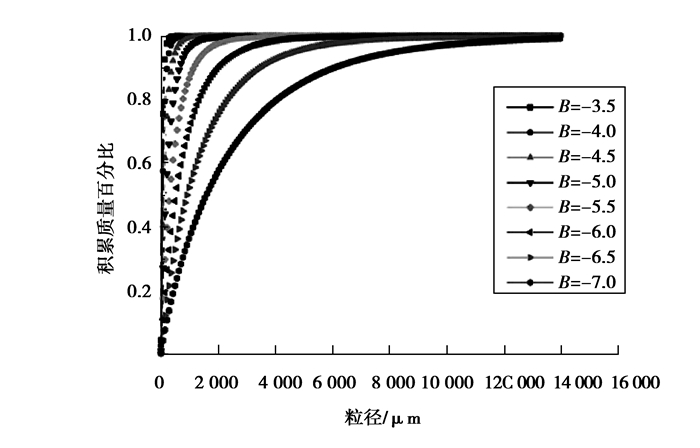
|
图7 B值对粒径分布曲线的影响 Fig. 7 The influence of B value on particle size distribution curve |
m为均匀性系数,控制整条曲线的形状。当m=1,它是指数分布;m=2时,是瑞利分布;当m=3.5时,近似正态分布。当m在小范围内变化时,可以使曲线产生和改变B相似的变化:m值越小,粒度分布范围越宽,且变化更加显著。这说明粒径级配曲线受m和B的综合影响。
m和B对颗粒级配的影响可以反映在m-B的二维平面中,平面中的每一个点都代表一种级配,本次颗分试验结果反映在mB空间中的情况如图 8。图 8表明,本次试验试样的级配在mB平面内呈带状分布,在m=1,B=-3.5附近较为集中。经计算得到m平均值0.92,标准差0.17;B平均值-3.7,标准差0.84。这表明在竖直方向上,细粒尾矿级配的m值变化很小,主要是B值发生变化,并且这种变化不是离散的,而是在中心值(m=0.92,B=-3.7)附近集中。
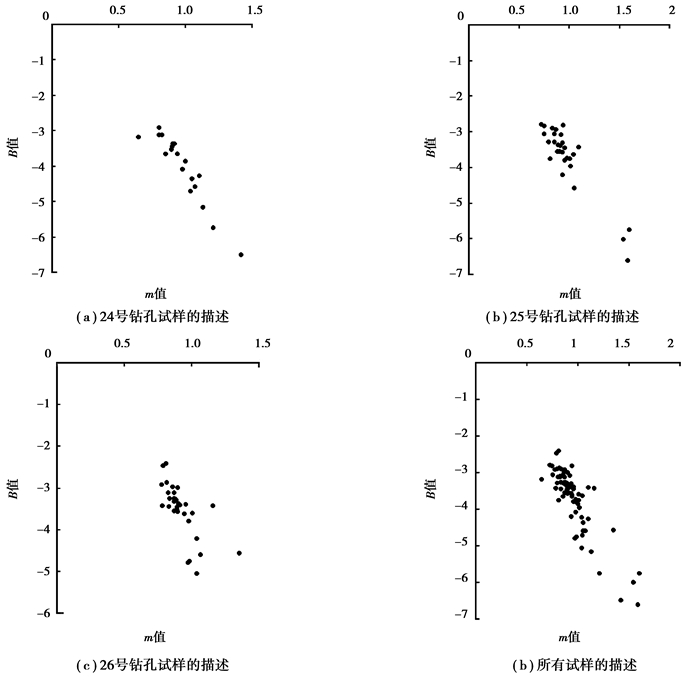
|
图8 试样级配在m-B平面的描述 Fig. 8 Sample grading in the m-B coordinates |
m-B平面为定量描述大数量试样的级配提供可能,其优点在于平面内的点和级配有一一对应的关系,但这种描述只适合于在X-Y坐标中具有线性关系的散体材料。
3 Weibull粒径分布模型与分形模型的关系在假定每级粒度的破碎率为常数,破碎过程有自相似规律的情况下,可以推导出以下公式[9]
| $y={{\left( x/d \right)}^{E-D}}$ | (16) |
式中:y指粒度为x时的筛下体积比例;E为拓扑维数,取E=3;D为分形维数。
根据筛下体积比例与筛下质量比例的关系,容易导出
| $F\left( x \right)={{\left( x/d \right)}^{E-D}}.$ | (17) |
据此对试样的质量分维数进行统计发现,试样的分维数大致在2.0~2.6之间,尤其集中在2.3~2.6,这符合岩石破碎分维数的一般经验,并接近自然材料破碎后最优级配曲线的分形维数2.5[17]。
对Weibull分布函数进行泰勒展开后得到
| $\begin{align} & F\left( x \right)={{\left( \frac{x}{\eta } \right)}^{m}}+R\left( x \right), \\ & R\left( x \right)=\frac{{{\text{e}}^{\theta }}{{\left( -\frac{x}{\eta } \right)}^{m}}}{2}\cdot {{\left( \frac{x}{\eta } \right)}^{2m}}. \\ \end{align}$ | (18) |
其中0<θ<1。
忽略R(x),有
| $F\left( x \right)\approx {{\left( \frac{x}{\eta } \right)}^{m}}.$ | (19) |
此时Weibull分布函数退化为GS函数,且m=E-D。对比式(3)和式(17),可发现b=E-D,说明G-S分布函数实质上就是一种分形分布,而G-S分布函数是Weibull分布函数的一种简单形式。
根据2.2的结果,用G-S分布函数数学模型描述粒径分布时,不如Weibull分布函数准确,这可能是假设条件“每级粒度的破碎率为常数”与实际情况有所出入造成的——由于细颗粒的强度大于粗颗粒(“尺度愈小、强度愈高”的观点在材料学里已得到广泛认可),其破碎的概率比大粒径的颗粒要小。破碎率与粒径的关系在Weibull分布中可以用R(x)考虑,这或许是Weibull分布函数与G-S分布函数本质上的不同之处。
4 细粒尾矿粒径分布形成机理的分级破坏假说从上文可知,细粒尾矿具有细粒多、粗粒少的粒径分布特征,这种现象可以用颗粒的分级破坏进行解释。首先,假设颗粒的粒径分布是多遍破碎的结果,在每一遍的破碎中,第n级粒径按破碎率Pn破碎为n+1级粒径(n=0,1,2,3,…)。考虑破碎率随粒径减小而减小,假设破碎率函数为
| ${{P}_{n}}={{0.5}^{n}}.$ | (20) |
其次,现实中的单颗颗粒破碎后会产生大小不一的各种粒径。这里假设一颗颗粒破碎后产生2颗体积为原体积1/2的颗粒,破碎函数表达式为
| $\begin{align} & F\left( x,y \right)=0,0\le x\le \frac{y}{2}; \\ & F\left( x,y \right)-1,x\ge \frac{y}{2}. \\ \end{align}$ | (21) |
式中:F(x,y)表示粒径为y的一颗颗粒破碎所产生的,粒度x<y的颗粒的数量积累百分比。
在上述条件下,设定初始时有100颗单粒体积为100单位的颗粒,那么经N=120遍破碎后的分布如表 5、表 6所示。其中Vn为第n级粒径单粒体积,Vn=1.562 5时不产生破碎。假设密度为1,则该粒径质量总和等于Vn与该粒径颗粒数量之积。表 5中颗粒数量中有小数出现,并且出现总体积和总质量“丢失”的情况,但这并不影响对整体分布的定性判断。
| 表5 细粒尾矿粒径分布的形成过程的模拟计算(颗粒数量)(1) Table 5 Simulation calculation of formation process of fine-grained tailings(grain number)(1) |
| 表6 细粒尾矿粒径分布的形成过程的模拟计算(颗粒质量)(2) Table 6 Simulation calculation of formation process of fine-grained tailings(grain quality)(2) |
根据表 5、表 6的结果,破碎开始后会在某一粒径产生数量和质量的峰值,这个峰值会随着N的增大移向下一粒径等级。当N的增大到一定程度(例子中N=10),颗粒数量和质量的分布会接近正态分布,之后粗粒越来越少而细粒越来越多,最后形成类似图 6的粒径分布。
|
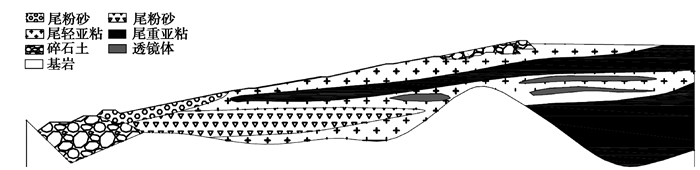
图9 细粒尾矿库剖面示意图 Fig. 9 Cutaway view of fine tailings pond |
虽然以上分析的破碎概率和破碎函数都基于假设,并且没有考虑尾矿破碎后的选矿、运输、沉积过程,但能够定性上反映细粒尾矿粒径分布形成过程的基本规律。
5 库内尾矿级配的区域化分布特征尾矿是水力充填坝,尾矿的沉积分布规律由尾矿粒径、排放方式、矿浆浓度等因素决定。图 9是甘肃某上游法细粒尾矿库概化剖面示意图,尾矿颗粒粒径按尾粉砂、尾亚砂、尾轻亚粘、尾重亚粘的分类顺序依次减小。从图中可以看出:尾粉砂和尾亚砂集中分布在坝体底部,达到一定坝高后坝体内尾矿以尾轻亚粘和尾重亚粘为主,这反映了筑坝初期排放尾矿颗粒粗,后逐渐变细的历史过程,是该矿选矿工艺改造、选矿细粒化造成的;从总体上看,颗粒粒径越大,沉积距离越近,加上分层筑坝方式的影响,各类尾矿形成的地层倾角与坝体坡度有趋同关系;当滩面的坡度较缓时,推移力变弱,细粒尾矿容易在滩面地势较低的区域和两扇形区交界处过早沉积,使得坝体重存在夹层和透镜体。
尾矿的粒径分布对尾矿的沉积特性有重要影响。在其他条件相同的情况下,细粒尾矿库沉积尾矿粒径分选性较差,更容易形成夹层和透镜体,不利于尾矿坝的稳定性。研究细粒尾矿的粒径分布规律,有利于我们更科学地评估尾矿坝稳定性。
6 结 论笔者以某尾矿坝细粒尾矿为研究对象,用筛分法和沉降法对82个样本进行了颗粒分析试验,在此基础上研究了细粒尾矿粒径分布规律研究及其运用,得出以下主要结论:
1) 用Weibull数学分布模型可以很好地描述、预测细粒尾矿粒径积累分布曲线,并估计粒径的概率密度曲线。使用这种模型描述细粒尾矿时,必须结合实际情况对曲线两端进行修正。
2) 用均匀性系数m和比例参数B能够完整表达细粒尾矿的分布特征。在m-B平面内描述本次颗分试样的结果具有带状特征,这种描述方式可以为描述颗粒级配的变化提供新的表达方式;
3) 分析了该尾矿试样的分形维数,与前人研究吻合。常用的分形模型对细粒尾矿粒径分布进行描述时的误差来源于破碎率的取值,而Weibull分布函数可以用特征数η来减小这种误差;
4) 在对Pn和F(x,y)进行假设后,模拟了矿石的破碎过程。结果表明,破碎过程中,粒径的概率密度分布会出现峰值,这个峰值会不断向粒径小的方向偏移,并最终呈现细粒多粗粒少的分布特点。
| [1] | 刘建立,徐绍辉,刘慧.几种土壤累积粒径分布模型的对比研究[J].水科学进展,2003,14(5):588-592. LIU Jianli, XU Shaohui, LIUHui. Investigation of different models to describe soil particle-size distribution data[J]. Advances in Water Science,2003,14(5):588-592.(in Chinese)( 1) 1) |
| [2] | Rosin P, Rammler E. The laws governing the fineness of powdered coal[J]. Journal of the Institute of Fuel,1993,7:29-36.( 1) 1) |
| [3] | Weibull W. A statistical distribution function of wide applicability[J]. Journal of Applied Mechanics,1951,18(3):293-297.( 1) 1) |
| [4] | Jopony M, Usup G, Mohamed M. Particle size Distribution of copper mine tailings from Lohan Ranau Sabah and its relationship with heavy metal content[J]. Pertanika,1987,10(1):37-40.( 1) 1) |
| [5] | Giuliano V, Pagnanelli F, Bornoroni L, et al. Toxic elements at a disused mine district:Particle size distribution and total concentration in stream sediments and mine tailings[J]. Journal of hazardous materials,2007,148(1):409-418.( 1) 1) |
| [6] | Gonzales P, Felix O, Alexander C, et al. Laboratory dust generation and size-dependent characterization of metal and metalloid-contaminated mine tailings deposits[J]. Journal of hazardous materials,2014,280:619-626.( 1) 1) |
| [7] | 郑钢镖,康天合,柴肇云,等.运用Rosin-Rammler分布函数研究煤尘粒径分布规律[J].太原理工大学学报,2006,37(3):317-319. ZHENG Gangbiao, KANG Tianhe, CHAI Zhaoyun, et al. Applied the Rosin-Rammler distribution function to study on the law of coal dust particle-size distribution[J]. Journal of Taiyuan University of Technology,2006,37(3):317-319.(in Chinese)( 1) 1) |
| [8] | 刘铁英,范利民.用双Rosin-Rammler函数求颗粒尺寸分布[J].上海理工大学学报,1998,20(2):135-138. LIU Tieying, FAN Liming, ZHENG Gang. A new algorithm for determination of the particle size distribution with bimodel Rosin-Rammler function[J]. Journal of University of Shanghai for Science and Technology,1998,20(2):135-138.(in Chinese)( 1) 1) |
| [9] | 李功伯,唐春安,徐小荷.岩石粉碎粒度G-S分布的分形几何描述[J].中国有色金属学报,1991,1(1):31-33. LI Gongbo, TANG Chunan, XU Xiaohe. Fractal geometry description of rock crushing granularity with the distribution of G-S[J]. China Nonferrous Metals,1991,1(1):31-33.(in Chinese)( 3) 3) |
| [10] | Mandelbrot B B. The fractal geometry of nature[M]. Macmillan,1983.( 1) 1) |
| [11] | 高峰,谢和平,赵鹏.岩石块度分布的分形性质及细观结构效应[J].岩石力学与工程学报,1994,13(3):240-246. GAO Feng, XIE Heping, ZHAO Peng. Fractal properties of size-frequency distribution of rock fragments and the influence of meso-structure[J]. Chinese Journal of Rock Mechanics and Engineering,1994,13(3):240-246.(in Chinese)( 1) 1) |
| [12] | 杨金玲, 李德成, 张甘霖, 等. 土壤颗粒粒径分布质量分形维数和体积分形维数的对比[J].土壤学报,2008,45(3):413-419. YANG Jingling, LI Decheng, ZHANG Ganlin, et al. Comparison of mass and volume fractal dimensions of soil particle size distributions[J]. Pedologica Sinica,2008,45(3):413-419.(in Chinese)( 1) 1) |
| [13] | 胡云锋,刘纪远,庄大方,等.不同土地利用/土地覆盖下土壤粒径分布的分维特征[J].土壤学报,2005,42(2):336-339. HU Yunfeng, LIU Jiyuan, ZHUANG Dafang, et al. Fractal dimension of soil particle size distribution under different land use/land coverage[J]. Pedologica Sinica,2005,42(2):336-339.(in Chinese)( 1) 1) |
| [14] | 张季如,朱瑞赓,祝文化.用粒径的数量分布表征的土壤分形特征[J].水利学报,2004,4(4):67-71. ZHANG Jiru, ZHU Rugeng, ZHU Wenhua. Fractal features of soils characterized by grain size distribution[J]. Journal of Hydraulic Engineering,2004,4(4):67-71.(in Chinese)( 1) 1) |
| [15] | Epstein B. Logarithmico-normal distribution in breakage of solids[J]. Industrial & Engineering Chemistry,1948,40(12):2289-2291.( 1) 1) |
| [16] | 谢和平,高峰.岩石类材料损伤演化的分形特征[J].岩石力学与工程学报,1991,10(1):74-82. XIE Heping, GAO Feng. The fractal features of the damage evolution of rock materials[J]. Chinese Journal of Rock Mechanics and Engineering,1991,10(1):74-82.(in Chinese)( 1) 1) |
| [17] | Wang J, Yan H. On the role of particle breakage in the shear failure behavior of granular soils by DEM[J]. International Journal for Numerical and Analytical Methods in Geomechanics,2013,37(8):832-854.( 1) 1) |
 2016, Vol. 39
2016, Vol. 39

