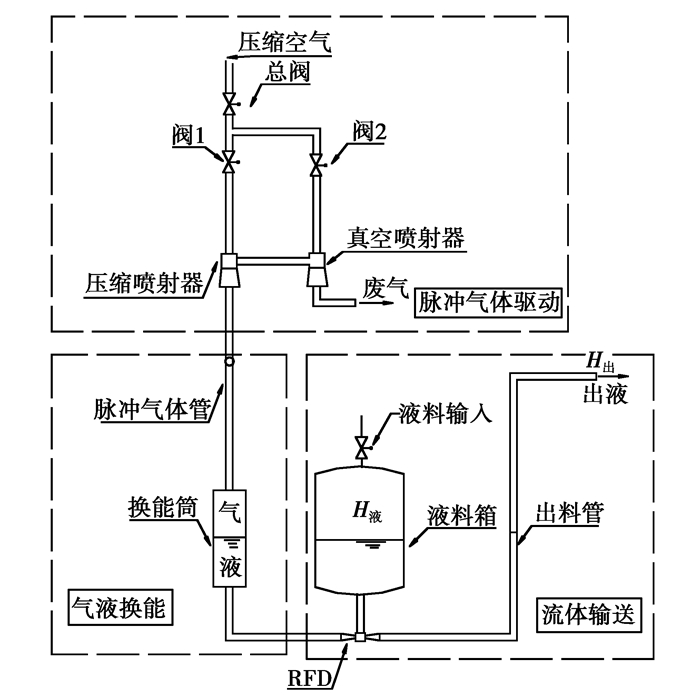
RFD是一种可用于输送含放射性、高温、剧毒、剧腐蚀等危险流体的免维修流体输送设备，其装置由脉冲气体发生单元、气液换能单元和流体输送单元组成。该装置以压缩空气为动力，由交替工作的喷射器产生脉冲气体并通过气液活塞运动产生脉冲液体，最终通过流体输送单元的RFD元件实现流动换向输出液体。周期性输送过程一般分为2个阶段，即反吸阶段将液料经由RFD先进入换能筒蓄能，压冲阶段再将换能筒中液料通过RFD直接送入出料管出料。由于完全依靠流体动力做功，不需要运动部件，设备低磨损，因此可以满足设计年限内免维修的要求，在核工业乏燃料后处理废液等危险流体的输送中具有广阔的应用前景^{[1, 2, 3]}。然而正是由于流体传能做功的特点，系统中各部件过流断面及其结构尺寸的设计至关重要，整个系统可按流体类别分为喷射器组及换能输送单元的换能筒、RFD、出料管以及液料箱输送管，前者是脉冲气体，通过脉冲压力控制后面液体段的脉冲运动，2部分相对独立。因此，为降低优化设计的维数和状态方程的复杂性，可考虑单独对液体段进行优化设计。由于优化目标包括效率和规模两方面因素，在限定设备尺寸的前提下，如何正确配套结构参数和运行参数，是获得最佳输送性能及稳定运行的关键。前期研究中，采用了枚举法和“边际效用”方法^{[4, 5]}，前者在解决维数较高的优化问题中，计算时间较长；后者改进了参数优选机制，优先选择对优化目标影响较大的参数，使方案收缩范围大大缩小，计算速度提高，但由于仅考虑单因素变化的关系，对于协同效应产生的最优方案很难获得，且在确定各参数的成本优化步长时，过于依赖设计者的意图或经验，很难科学量化^[6]；综上所述，仍需要对寻优方法进行改进，文中将讨论采用遗传算法解决上述问题^{[7, 8, 9]}。 1 RFD装置优化设计模型

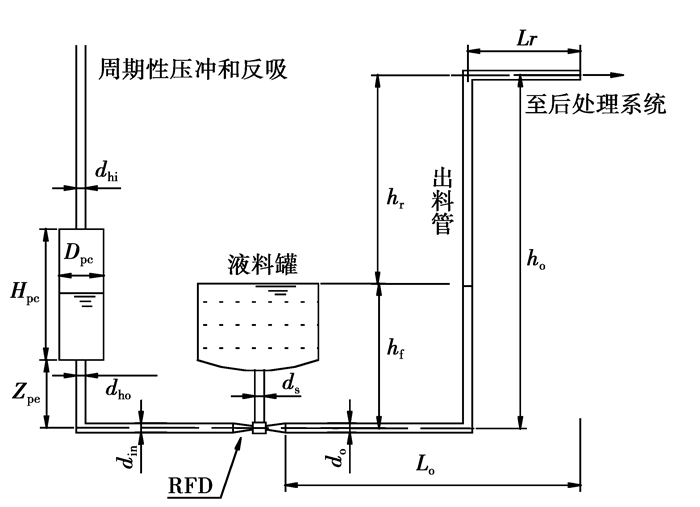
RFD装置作为一种流体输送设备，由脉冲气体发生单元、气液换能单元和流体输送单元组成(见图 1)。其设计的优化目标是以最小的系统规模达到最佳的输送性能。考虑单独对液体段进行优化设计的计算图如图 2所示。对于多目标问题，应根据用户需要进行权衡。首先，输送性能应满足用户流量和扬程指标，尽量保持较高效率；其次，系统规模主要体现在装置造价以及布置安装的限制方面，相比于输送性能，其重要性较弱，规模可以根据用户需要进行设置。综上所述，在RFD系统的优化设计过程中，将着重考虑系统输送性能的优化，同时兼顾系统规模的控制。具体做法是，以满足用户指定平均流量、扬程及参数约束条件的方案为有效方案，其输送性能和规模分别用效率N和运行周期T反映，提出复合优化判据

图1(Fig. 1)

图1 RFD装置组成示意图 Fig. 1 Schematic of RFD set

图2(Fig. 2)

图2 RFD装置计算简图 Fig. 2 Schematic for calculation of RFD set

式中：N为系统效率；T为系统周期，作为系统规模大小的衡量标准；n为装置规模指数，其值取0~1，越大表明装置越小。复合判据K越大，表明设计结果不仅能满足应用指标要求(流量、扬程、规模)且效率较高。由此，通过复合优化判据将多目标问题简化为单目标问题。现将RFD装置运行数学模型简述如下^{[1, 2]}。 1.1 流量计算

首先将RFD系统简化为孔口出流模型，然后计算RFD系统运行1个周期所输送的流体体积，除以周期而得出平均流量

式中：V_o为压冲阶段出料管出流体积；V_r为倒流体积；Δt_p、Δt_rf分别为压冲、反吸阶段时间，其和为周期T，其中，压冲时间为

式中：A_pc、A_t分别为换能筒横截面积和RFD喷嘴面积；C_d压冲流量系数，由试验装置确定；P_t为RFD浸没压力。反吸时间为

式中C_drf为反吸流量系数。

压冲阶段出料体积为

式中Q_o为压冲阶段出料管出流流量：

式中：P_o为RFD下喷嘴后端压力；C_p为扩散管阻力系数。

式中：h_o为出料管垂直高度；L_o为出料管水平长度；f为沿程阻力系数；K为局部阻力系数；A_o为出料管过流面积。

压冲阶段结束后，出料管回流体积

结合式(2)~式(8)，即可得到系统的平均流量Q_ra。 1.2 效率计算

效率实际上是指能量的利用率，即周期内的平均效率等于有用功与输入总功之比，可推导出RFD装置做功平均效率为

式中：V_pc为换能筒体积；H_pch为换能筒底部距RFD喷嘴的高度；其余同上。

针对上述水力模型及优化目标，以W和M分别表示系统性能和规模。根据数值仿真和试验，如图 2所示，需要优化的参数有：换能筒直径D_pc、换能筒高度h_pc、RFD浸没深h_f、压冲压力P_i、反吸压力P_r、喷嘴直径d_t、出料管直径d_o，将RFD的输送性能和系统规模可以表述为上述自变量的函数，即状态方程：

以上各个参数根据实际工程应用要求都有着各自的定义域，同时考虑到参数配套尺寸约束，优化目标是在满足流量的前提下使得效率最高且规模最小，数学模型如下：

鉴于传统枚举法和边际效用方法在寻优方面遇到的问题，笔者拟采用遗传算法求解上述高维优化问题^{[10, 11, 12]}。目前遗传算法应用中的问题包括：1)适应度值标定方式多种多样，且无简洁、通用的方法；2)由于变异概率过低而产生的早熟现象；3)接近最优解时收敛性不好。为改进实际计算性能通常需要解决以下问题：确定编码方案，标定适应度函数，选择遗传操作方式及相关控制参数，确定停止准则等。文中定义适应度函数如下：①若流量小于1.1倍用户要求流量，则适应度值为10；②若流量大于1.2倍用户要求的流量，则适应度值为5；③若流量介于1.1~1.2倍用户要求流量，则适应度值为4；④若满足条件3，且倒流比大于8，则适应度值为3；⑤若满足条件4，且换能筒高径比介于2.0~3.0之间，则适应度值为2；⑥若满足条件5，且分流比介于0.9~1.1之间，则适应度值为1；⑦若满足条件6且周期小于1 000 s，即为有效方案，继续优化判断则利用复合优化判据K定义适应度值(-K)，该值越小越好。

在运行遗传算法程序时，需要对包括交叉概率、变异概率、种群的大小、染色体长度、代沟、最大进化代数等参数进行设置，它们对遗传算法的性能都有很重要的影响，甚至会影响到整个算法的收敛性。交叉概率一般建议取值范围是0.4~0.99，文中选择0.7；变异概率的选取一般受种群大小、染色体长度等因素的影响，通常选取很小的值以避免引起种群的不稳定，但过小易产生未成熟收敛，文中采用高斯变异；种群大小直接影响到遗传算法的收敛性或计算效率，根据实际情况一般在10~200之间选定，通过试验，文中选择种群大小为200，可满足全局收敛到极值点；最大进化代数作为一种算法终止条件，取2 000代。 3 优化设计算例分析 3.1 遗传算法主要参数的确定

计算前，在适应度函数中给定扩散管压力回升参数，喷嘴反吸流量系数，出料管总阻力系数及喷嘴流量系数，输入要设计的RFD流量和扬程要求，定义适应度函数，变量个数为7，种群大小取200，根据各变量的取值范围定义初始种群的向量范围，交叉概率取0.7。变异操作选择高斯变异，为了使计算更快收敛到全局最优，参数尺度(scale)取0.5，压缩系数(shrink)取1。计算步数取2 000。 3.2 实例及计算结果比较分析

运用遗传算法程序进行优化设计，计算1个工况大概耗时为100 s左右。以设计参数Q=5 m³/h，H=15 m为例说明遗传算法与枚举法计算结果的差别。如表 1所示，3种方法喷嘴直径相差不大(5%)；相同条件下，遗传算法一般可得到较小的装置规模和较高的水力效率；边际效用法更适用于中、小规模样机的设计，而此时遗传算法结果与边际效用法接近，且有更高效率；遗传算法所需的压冲压力普遍小于其他算法。因此得到如下结论。

表1(Table 1)

表1 遗传算法与枚举法计算结果的对比Table 1 Comparison of the calculation results of genetic algorithm and enumeration method 方法 规模 dt/mm do/mm hpc/m Dpc/mm Pr/MPa Pi/MPa Qra/ (m3·h-1) N/% N/Tn 遗传 22 88 2.5 965 5 2.1 5.56 58.2 58.2 边际 n=0 23 98 2.9 900 5 2.0 5.74 57.7 57.7 枚举 22 79 2.8 900 5 3.0 5.92 56.5 56.5 遗传 23 71 1.7 659 5 2.2 5.53 52.2 16.5 边际 n=0.2 24 98 2.2 800 5 2.0 5.99 53.9 20.3 枚举 22 79 2.1 750 5 3.0 5.73 53 15.3 遗传 n=0.4 23.7 67 1.6 635 5 2.2 5.56 49.5 5.5 边际 21 49 1.4 500 5 3.0 5.57 37.5 8.4 枚举 23 79 2.1 750 4.5 3.0 5.86 52.4 4.4 遗传 22.6 65 1.6 608 5.0 2.3 5.61 49.1 1.8 边际 n=0.6 21.0 49 1.4 500 5.0 3 5.64 36.9 3.9 枚举 23.0 79 2.4 700 4.5 3 6.00 51.6 1.3 遗传 22.9 65 1.6 611 5 2.3 5.57 46.7 0.2 边际 n=1 23.0 49 1.9 460 3 2.9 5.55 39.3 0.16 枚举 21.0 49 1.4 500 5 3 5.57 37.5 0.11

表1 遗传算法与枚举法计算结果的对比 Table 1 Comparison of the calculation results of genetic algorithm and enumeration method

1) 传统枚举法计算结果稳定可靠，对设计参数在取值范围内的所有组合进行了全面计算，但计算精度依赖于步长精度，极大影响计算时长。

2) 边际效用方法以影响度最高参数优先“递增”的方式寻优，计算精度依赖于步长，在所需设计规模较小情况，计算结果与枚举法接近，反之偏差较大。由于采用单因素改变方式寻优，无法考虑因素间的协同效应，因此一般难以获得最好的参数组合。

3) 遗传算法采用随机方式寻优，设计参数满足约束条件，连续搜索最优解，不存在受步长限制问题，可考虑各因素间的协同优化效果，经过改进计算结果已基本稳定。 3.3 根据输送要求设计RFD装置及其运行参数

取规模权重n=0.5，根据需要流量和扬程进行设计，计算结果如表 2、表 3所示。由计算结果可知，扬程一定的条件下，随着流量的增大，RFD的压冲压力P_i和反吸压力P_r基本不变，但RFD喷嘴直径D_t、出料管直径D_o、换能筒高H_pc和直径D_pc等关键断面尺寸都有增大的趋势，符合流量变化规律；其次，流量一定时，随着扬程的增大，RFD所有参数值都有增大的趋势。扬程增大，做功增加，所以压冲压力P_i必然增大；为了保证系统具有较高的效率，换能筒体积也必然增大。

表2(Table 2)

表2 扬程一定，不同流量下RFD装置设计结果比较Table 2 Design parameters of RFD sets under different flow rates (fixed head) 扬程/m 流量/(m3·s-1) hf/m do/mm hpc/m Pi/MPa Pr/MPa Dpc/mm dt/mm 3 0.7 48 1.2 2 -0.5 450 16 5 1.4 59 1.4 2 -0.5 516 20 10 10 1.46 80 1.7 2 -0.5 634 29 15 1.2 97 1.9 2 -0.5 727 36 20 1.7 106 2 2 -0.5 773 40 3 0.2 53 1.4 2.3 -0.5 540 18 5 0.2 67 1.6 2.3 -0.5 630 23 15 10 0.2 89 2.0 2.3 -0.5 750 33 15 0.4 107 2.2 2.3 -0.5 850 40 20 1.8 115 2.4 2.6 -0.5 900 40 20 3 0.2 57 1.6 3 -0.5 620 18 5 0.2 73 1.9 3 -0.5 730 23 10 0.4 95 2.3 3 -0.5 850 33 15 0.8 114 2.5 3 -0.5 980 40

表2 扬程一定，不同流量下RFD装置设计结果比较 Table 2 Design parameters of RFD sets under different flow rates (fixed head)

表3(Table 3)

表3 流量一定，不同扬程下RFD装置设计结果比较Table 3 Design parameters of RFD sets under different heads (fixed flow rate) 流量/(m3·s-1) 扬程/m hf/m do/mm hpc/m Pi/MPa Pr/MPa Dpc/mm dt/mm 3 10 0.7 48 1.2 2 -0.5 450 16 12 0.2 51 1.3 2 -0.5 490 17 15 0.2 53 1.4 2.3 -0.5 540 18 20 0.2 57 1.6 3 -0.5 620 18 5 10 1.4 59 1.4 2 -0.5 516 20 12 0.2 64 1.5 2 -0.5 580 22 15 0.2 67 1.6 2.3 -0.5 630 23 20 0.2 73 1.9 3 -0.5 730 23 10 10 1.46 80 1.7 2 -0.5 634 29 12 0.2 85 1.8 2 -0.5 700 31.5 15 0.2 89 2.0 2.3 -0.5 750 33 20 0.4 95 2.3 3 -0.5 850 33

表3 流量一定，不同扬程下RFD装置设计结果比较 Table 3 Design parameters of RFD sets under different heads (fixed flow rate)

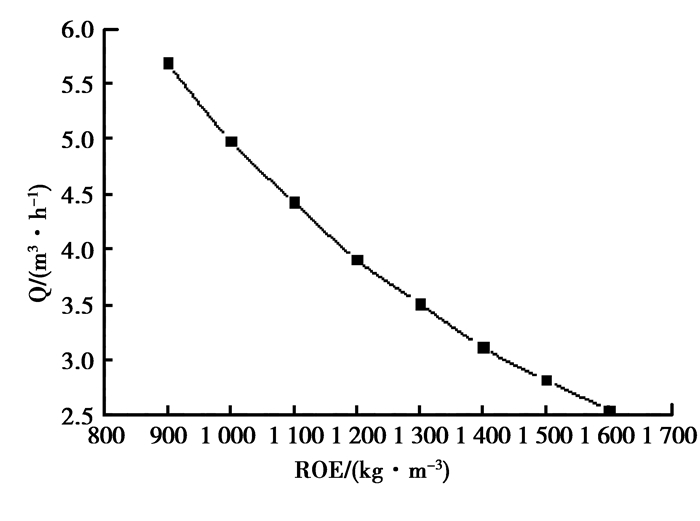
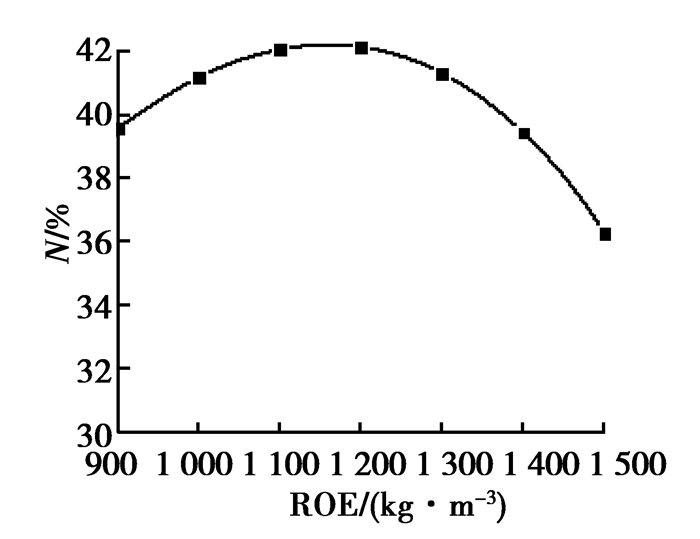
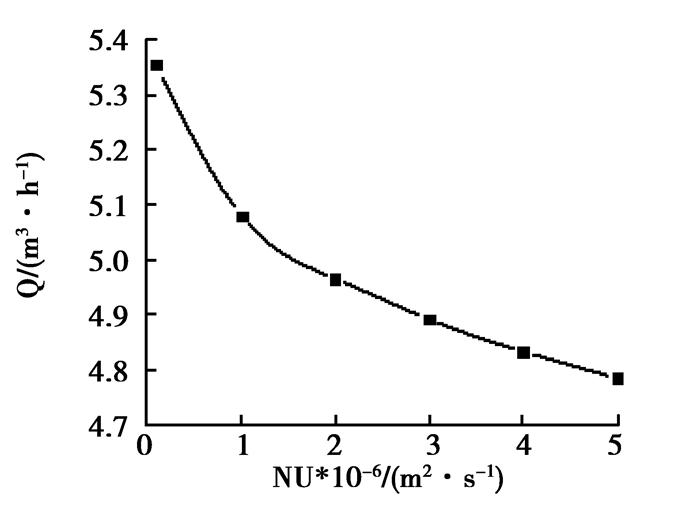
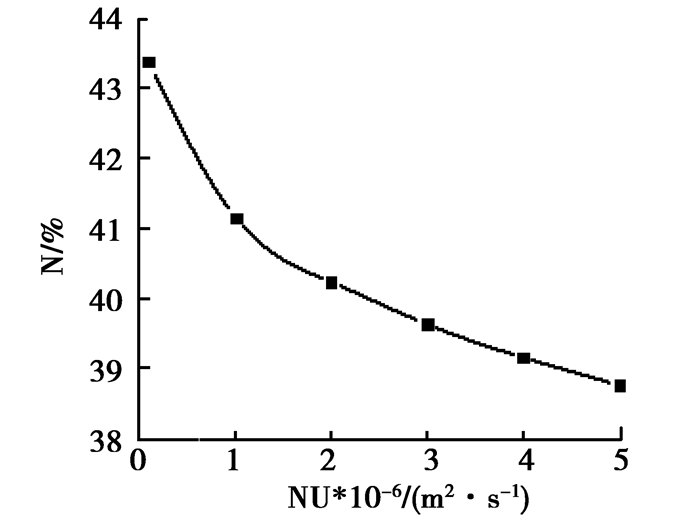
实际工程应用中，输送介质的密度、温度、粘度对装置的输送性能会产生影响，需要研究运行性能的换算规律。在流量为3 m³/h，扬程为15 m，装置规模指数n=0.5的工况下，改变介质密度和粘度值进行RFD装置设计发现，结构参数的变化并不明显，但的确影响了装置运行特性。以某RFD装置设计结果为例，根据典型工业流体的物性参数，改变密度变化范围900~1 600(kg/m³)，得到装置流量和效率随密度变化曲线，如图 3、图 4所示。由图可知，密度变大时，虽然扬程不变，但输入能量一定的条件下，平均流量必然递减，而水力效率则呈现先增大后减小的趋势，与管道的输送能力有关，存在一个系统运行高效区。进一步取粘度变化范围：0.1~5(×10^-6 m²/s)，分别计算出相应的流量和效率，得到装置流量随粘度变化曲线(如图 5、图 6所示)。由于输送阻力随粘度的增大而增大，能量以摩擦的形式耗散，所以无论是平均流量还是效率都呈现递减的趋势。

图3(Fig. 3)

图3 流量随密度变化图 Fig. 3 Variation of flow with density

图4(Fig. 4)

图4 效率随密度变化图 Fig. 4 Variation of efficiency with density

图5(Fig. 5)

图5 流量随粘度变化图 Fig. 5 Variation of flow with viscosity

图6(Fig. 6)

图6 效率随粘度变化图 Fig. 6 Variation of efficiency with viscosity

1) 基于遗传算法对RFD装置多目标高维优化模型的求解展开研究，采用了随机方式搜索全局空间，能获得比枚举法和边际效用法更优的计算结果，且计算效率大大提高。

2) 针对遗传算法在多目标情况下无法得到合理优化结果问题，通过引入复合优化判据摸索出改善遗传算法稳定性和收敛性的控制参数。

3) 利用遗传算法对RFD结构参数和运行参数进行系列化设计，总结了流量、扬程对RFD装置关键尺寸及运行参数的影响规律。

4) 针对不同的介质密度和粘度对RFD装置结构参数和运行参数的影响进行了分析，给出了不同密度和粘度下，RFD装置输送流量的换算关系。