2. 三峡大学 土木与建筑学院, 湖北 宜昌 443002
2. Civil and Architectural Institute, China Three Gorges University, Yichang 443002, Hubei, P. R. China
随着三峡库区后续规划工作的深入开展,越来越多的道路开始在三峡库区兴建,库区对筑路材料的需求量日益增大。三峡库区地形以山地为主,交通运输十分不便,库区分布着大量强度相对较低的风化砂。这些风化砂是地表岩层风化过程的中间产物,其耐久性较一般的土料差,风化砂颗粒呈棱角状,粒径大小分布不均匀,没有规则的几何形状,物理力学性质较不稳定,受力后颗粒容易破碎,整体强度较低[1, 2, 3, 4, 5]。能否解决风化砂的强度问题,使之达到路用标准,对就地取材、节约成本,推动库区经济建设具有相当重要的意义。因此,针对风化砂的不良特性,文中拟采用水泥对其进行稳定,以提高稳定后风化砂的整体强度,使其达到路面基层的规范要求。
回弹模量是表征强度的重要力学指标之一,它是指路基、路面及筑路材料在荷载作用下产生的应力与其相应的回弹应变的比值,是路面结构设计中必不可少的设计参数:在弹性变形阶段内和垂直荷载作用下,如果垂直荷载为定值,回弹模量值愈大则产生的垂直位移就愈小;如果竖向位移是定值,回弹模量值愈大,则表示能承受外荷载作用的能力就愈大,因此,路面设计中通常采用回弹模量作为抗压强度的指标[6, 7, 8, 9]。文中以三峡库区宜昌市夷陵区太平溪镇百岁溪处的风化砂为研究对象,主要研究了不同养护龄期和水泥掺量下水泥稳定风化砂抗压回弹模量的变化规律,重点分析了水泥稳定风化砂抗压强度形成的原理及抗压回弹模量的变化规律,在此基础上建立了水泥稳定风化砂抗压回弹模量与水泥掺量、养护龄期的数学模型;最后,将补充试验的结果与模型计算结果进行对比,验证了数学模型的正确性及精确程度,为三峡库区风化砂大规模应用于路面基层提供了一定的参考依据。
1 试验材料及试验方案 1.1 风化砂试验所用风化砂取自湖北省宜昌市夷陵区太平溪镇百岁溪处,风化砂颜色为土黄色,粒径大小分布不均匀、没有规则的几何形状,棱角显著,本身强度较低,较大砂颗粒在外力作用下容易破碎,大部分风化砂是由花岗岩风化而成的。经过一系列室内实验,得到了风化砂的颗粒分布、天然含水率、含泥量等基本物理性质指标,如表 1、表 2所示。
| 表 1 风化砂的颗粒粒径分布 Table 1 The particle size distribution of weathered sand |
| 表 2 风化砂的基本物理性质指标 Table 2 The basic physical characteristics of weathered sand |
从表 1可以看出:试验风化砂颗粒的主要粒径在10~0.5 mm范围内,大约为83.02%;粒径10 mm以上的只占3.34%;该风化砂的不均匀系数为Cu=10.21,曲率系数Cc=3.08,初步判定试验用风化砂为级配不良砂。
从表 2的数据可以看出:试验所用风化砂的含泥量较小,达到了规范对公路基层材料的要求。
1.2 水泥试验所用水泥为市场上销售的Po32.5普通硅酸盐水泥,具有良好的和易性、保水性、耐磨性和抗冻性等性质[10, 11, 12]。水泥的基本物理指标如表 3所示。
| 表 3 水泥的各项物理试验指标 Table 3 The physical test indexes of cement |
试验参照《公路工程无机结合料稳定材料试验规程》(JTG E51—2009)中的承载板法进行,水泥掺量分别为3%、5%、7%、9%,然后由重型击实试验得到每种水泥掺量下水泥稳定风化砂的最佳含水率和最大干密度[13, 14, 15, 16]。在不同水泥掺量下,均按最佳含水率和最大干密度制样,试样的养护龄期分别为7、14、21、28、35、56、70 d。试样制作及试验过程如图 1、图 2所示。

|
图 1 重型击实制样 Fig. 1 The heavy compaction sample |

|
图 2 回弹模量试验过程 Fig. 2 The process of modulus of resilience test |
具体试验操作过程如下:
1) 将风化砂在自然状况下风干过5 mm标准筛,每个试件取风化砂5 kg左右,测定其风干含水量,然后加入一定质量的水分(预留2%),使之达到要求的含水量后装入密闭塑料袋闷放一昼夜备用。 2) 加入预设质量的水泥和预留2%的水,拌合均匀后分3层倒入试模内,进行击实成型,击实完毕后将风化砂的表面刮平。3) 每组试件制备3个试样,放在标准养护间内进行养护。
抗压回弹模量可按下式计算
| Ec=πpD4l(1−μ2), | (1) |
按照试验规程,根据上述方法进行回弹模量试验,可以得出水泥稳定风化砂在不同掺量和养护龄期下的回弹模量,试验结果见表 4。
| 表 4 不同水泥掺量和养护龄期下水泥稳定风化砂回弹模量MPa Table 4 The modulus of resilience of cement stabilized weathered sand under different cement content and curing age MPa |
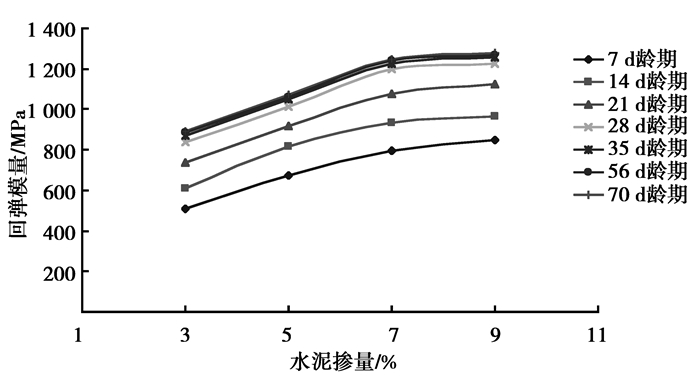
根据表 4中的数据,以水泥掺量为横坐标,以抗压回弹模量值为纵坐标,可绘出养护龄期分别为7、14、21、28、35、56、70 d,回弹模量值随水泥掺量的变化曲线图,如图 3所示。
|
图 3 不同养护龄期,水泥掺量与回弹模量值关系曲线 Fig. 3 The relationship curves between cement content and modulus of resilience under different curing age |
从表 4和图 3可以看出:
水泥可以显著提高风化砂的抗压回弹模量,在相同的养护龄期下,水泥稳定风化砂的抗压回弹模量随水泥掺量的增加而明显增大,且抗压回弹模量在水泥掺量3%~7%之间增长速度较快,在水泥掺量7%~9%之间增长较慢,基本上趋于稳定。在各养护龄期下,水泥稳定风化砂抗压回弹模量值均随着水泥掺量的增加,增长的幅度也在逐渐减慢。
当养护龄期为7 d时,抗压回弹模量在水泥掺量3%~7%之间增长了282.28 MPa,在7%~9%之间只增长了56.72 MPa;当养护龄期为14 d时,抗压回弹模量在水泥掺量3%~7%之间增长了323.77 MPa,而在7%~9%之间时只增长了34.67 MPa;当养护龄期为21 d时,抗压回弹模量在水泥掺量3%~7%之间增长了341.93 MPa,在7%~9%之间时只增长了48.25 MPa;当养护龄期为28 d时,抗压回弹模量在水泥掺量3%~7%之间增长了359.15 MPa,在7%~9%之间时只增长了27.21 MPa;当养护龄期为35 d时,抗压回弹模量在水泥掺量3%~7%之间增长了357.87 MPa,在7%~9%之间时增长了29.6 MPa;当养护龄期为56 d时,抗压回弹模量在水泥掺量3%~7%之间增长了353.14 MPa,在7%~9%之间时只增长了30.19 MPa;当养护龄期为70 d时,抗压回弹模量在水泥掺量3%~7%之间增长了353.28 MPa,在7%~9%之间时只增长了30.74 MPa。产生这一现象的主要原因是:在风化砂中掺入水泥后,水泥充斥在风化砂颗粒的缝隙之间,当水泥发生水化等硬凝胶结作用时,将促使风化砂颗粒胶结在一起,形成一个稳定的整体,水泥的系列化学反应生成了许多不溶于水的结晶物质,最终促使水泥稳定风化砂抗压回弹模量大幅提高;当水泥掺量超过一定用量后,水泥用量越多,干缩越厉害,产生的微观干缩裂缝会导致强度下降,抵消一部分水泥水化胶凝作用产生的强度,因此,抗压回弹模量在水泥掺量7%~9%之间基本趋于稳定。
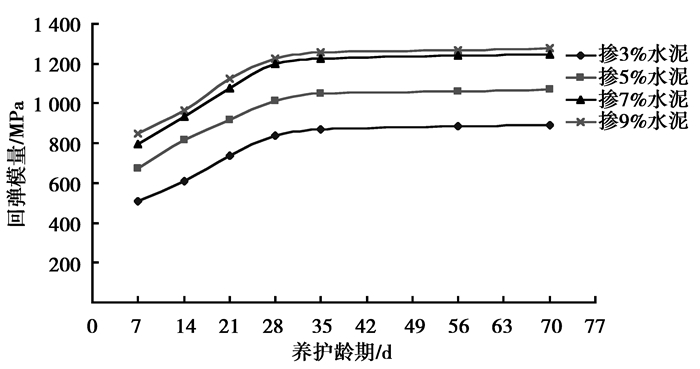
2.2 养护龄期对水泥稳定风化砂抗压回弹模量的影响及分析根据表 4中的数据,以养护龄期为横坐标,以抗压回弹模量值为纵坐标,可绘出水泥掺量分别为3%、5%、7%、9%,回弹模量值随养护龄期的变化曲线图,如图 4所示。
|
图 4 不同水泥掺量,养护龄期与回弹模量值关系曲线 Fig. 4 The relationship curves between curing age and modulus of resilience under different cement content |
从表 4和图 4可以看出:
养护龄期对水泥稳定风化砂的抗压回弹模量影响十分显著,在相同的水泥掺量下,随着养护龄期的逐渐增长,水泥稳定风化砂的抗压回弹模量迅速增大,当养护龄期达到28 d以后,随着龄期的增长,回弹模量的增长速率非常缓慢,基本趋于稳定。
当水泥掺量为3%时,养护28 d的回弹模量占整个养护观测期(70 d)的93.93%;当水泥掺量为5%时,养护28 d的回弹模量占整个养护观测期(70 d)的94.72%;当水泥掺量为7%时,养护28 d的回弹模量占整个养护观测期(70 d)的96.12%;当水泥掺量为9%时,养护28 d的回弹模量占整个养护观测期(70 d)的95.94%。产生这种现象的原因是:风化砂本身的强度较低,掺入水泥后,依靠水泥的水化作用产生胶凝物质,从而提高了整体强度,水泥水化反应需要一个时间段,在最初的28 d,随着水化反应的迅速进行,水泥稳定风化砂的强度不断增加,抗压回弹模量亦不断增长;在28 d之后,水泥的水化反应基本完成,强度的增长也就基本稳定下来。
3 数学模型的建立及评估 3.1 数学模型的建立根据表 4中的数据及图 3所示的曲线图形,对各养护龄期下,水泥掺量与抗压回弹模量值进行回归分析,建立起相应的数学模型,如表 5所示。
| 表 5 不同养护龄期下,回弹模量与水泥掺量的函数关系 Table 5 The function relationship between modulus of resilience and cement content under different curing age |
从表 5可以看出,在各养护龄期下,水泥掺量与抗压回弹模量值之间存在着较好的对数函数关系。
根据表 4中的数据及图 4所示的曲线图形,对各水泥掺量下,养护龄期与抗压回弹模量值进行回归分析,建立起相应的数学模型,如表 6所示。
| 表 6 不同水泥掺量,回弹模量与养护龄期的函数关系 Table 6 The function relationship between modulus of resilience and curing age under different cement content |
从表 6可以看出,在各水泥掺量下,养护龄期与抗压回弹模量值之间表现出明显的线性变化关系。
根据试验数据,通过将养护龄期和水泥掺量与抗压回弹模量值进行二元回归分析,建立了相应的数学模型,得到三者之间的二元计算分析模型:
| Ec=[40.466ln(m)+235.94]∙ln(n)+373.12ln(m)+872.96,(0≤m<35); | (2) |
| Ec=(0.0069m2−0.8339m+394.12)∙ln(n)+0.014m2−1.2086m+2204.4,(35<m≤70). | (3) |
通过回归分析,分别建立起了不同水泥掺量下,养护龄期与抗压回弹模量值及不同养护龄期下,水泥掺量与抗压回弹模量值之间的数学模型。为进一步验证上述模型的正确性及精确度,制作水泥掺量分别为2%、4%、6%、8%的试件,养护7、14、21、28、35、56、70 d;制作水泥掺量分别为3%、5%、7%、9%的试件养护5、10、25、42、63 d,然后进行回弹模量试验,并将试验结果与理论计算值相比较,采用相对误差值对各数学模型进行评估。如表 7、表 8所示。
| 表 7 不同养护龄期下,回弹模量值与水泥掺量评估结果 Table 7 The evaluation results between modulus of resilience and cement content under different curing age |
| 表 8 不同水泥掺量下,回弹模量值与养护龄期评估结果 Table 8 The evaluation results between modulus of resilience and curing age under different cement content |
从上述2表的计算结果可以看出,相对误差值均较小,大多分布在2%~3%之间,最大相对误差值为4.1%,所有的相对误差值均控制在5%之内,表明文中所建立的数学模型具有较高的精度,能较好地表达各变量之间的关系。
4 结 论通过大量的试验数据,研究了不同水泥掺量、不同养护龄期对水泥稳定风化砂抗压回弹模量值的影响,利用回归分析方法,建立起了3者之间的数学模型。在此基础上,通过补充室内试验与理论计算值进行比较,验证了模型的正确性及精确性,得出了如下结论。
1) 水泥可以显著提高风化砂的整体刚度,且当水泥用量达到一定值后,水泥稳定风化砂可以用作高速公路的基层填料;
2) 在相同的养护龄期下,水泥稳定风化砂的抗压回弹模量随水泥掺量的增加而显著增大,增长的幅度先快后慢,2者之间呈现良好的对数函数关系;
3) 在相同的水泥掺量下,随着养护龄期的增长,水泥稳定风化砂的抗压回弹模量值在最初的28 d内迅速增大,此后回弹模量的增长进入相对稳定阶段,且增长的速度非常缓慢,回弹模量值与养护龄期之间呈线性增长的关系。
4) 养护龄期和水泥掺量均对抗压回弹模量有较大的影响,通过试验数据对3者之间的分析,得到了3者之间了二元回归方程式。
| [1] | 安彦卿.稳定风化砂在高速公路中的应用[D].西安:长安大学,2005. AN Yanqing. Stable weathered sand in highway application[D]. Xian:Chang'an University, 2005.(in Chinese)( 1) 1) |
| [2] | 韩雪梅,杨建英,辜再元,等.强风化砂岩夹板岩重塑土的剪切强度特性[J].中国水土保持科学,2012,10(2):55-60. HAN Xuemei, YANG Jianying, GU Zaiyuan, et al. A shear strength property of remolded soil of weathered sandstone splint rock[J]. Science of Soil and Water Conservation, 2012, 10(2):55-60.(in Chinese)( 1) 1) |
| [3] | 高韬.稳定风化砂在高速公路中的应用[D].西安:长安大学,2009. GAO Tao. Stability weathered sand in highway application[D]. Xi'an:Chang'an University, 2009.(in Chinese)( 1) 1) |
| [4] | 弋晓明,李术才,王松根,等.非饱和粉土回弹模量的应力依赖性与水敏感性耦合分析[J].山东大学大学学报(工学版),2013,43(2):84-88. GE Xiaoming, LI shucai, WANG songgen, et al. Coupling analysis of stress dependence and water sensitivity for resilient modulus of unsaturated silt soil[J]. Journal of Shandong University(Engineering science), 2013, 43(2):84-88.(in Chinese)( 1) 1) |
| [5] | 赵延庆,薛成,黄荣华. 沥青混合料抗压回弹模量与动态模量比较分析[J].武汉理工大学学报,2007,29(12):105-107. ZHAO Yanqing, XUE Cheng, Huang Ronghua. Comparison of compressive resilient modulus and dynamic modulus of asphalt mixtures[J]. Journal of WuHan University of Technology, 2007, 29(12):105-107.(in Chinese)( 1) 1) |
| [6] | 石鸿.公路土基回弹模量承载板试验方法研究[J].公路交通技术,2011(4):1-5. SHI Hong. Research on test method for modulus of resilience bearing plates on highway soil roadbed[J]. Technology of Highway and Transport, 2011(4):1-5.(in Chinese)( 1) 1) |
| [7] | 凌建明,苏华才,谢华昌,等. 路基土动态回弹模量的试验研究[J]. 地下空间与工程学报,2010,6(5):919-925. LING Jianming, SU Huacai, XIE Huachang, et al. Laboratory research on dynamic resilient modulus of subgrade soil[J]. Chinese Journal of Underground Space and Engineering, 2010, 6(5):919-925.(in Chinese)( 1) 1) |
| [8] | 陈开圣,胡鑫.高液限红黏土回弹模量试验[J].公路,2010(4):143-147. CHEN Kaisheng, HU Xin. Resilent modulus test of high liquid red clay[J]. Highway, 2010(4):143-147.(in Chinese)( 1) 1) |
| [9] | 董城,冷伍明,李志勇,等. 水泥改良高液限黏土动态回弹模量试验研究[J].岩土力学, 2013, 34(1):133-138. DONG Cheng,LENG Wuming,LI Zhiyong,et al. Experimental study of dynamic resilient modulus of cement-improved high liquid limit clay[J]. Rock and Soil Mechanics, 2013, 34(1):133-138.(in Chinese)( 1) 1) |
| [10] | 肖军华.循环荷载下压实粉土的回弹模量试验研究[J].公路,2010(8):199-205. XIAO Junhua. Experiment and study on resilient modulus of compacted silt under cyclic loading[J]. Highway, 2010(8):199-205.(in Chinese)( 1) 1) |
| [11] | 郑伟.水泥稳定土无侧限抗压强度、抗压回弹模量与龄期的关系[J]. 内蒙古公路与运输,2013(3):57-59. ZHENG Wei. Cement stabilized soil unconfined compressive strength, compressive modulus of relationship with age[J]. Highways and Transportation in inner Mongolia, 2013(3):57-59.(in Chinese)( 1) 1) |
| [12] | 王海鹏,韩春鹏.冻融循环作用对石灰改良黏土侧限回弹模量的影响[J].长安大学学报(自然科学版),2013, 33(2):33-37. WANG Haipeng,HAN Chunpeng. Effect of freeze and thaw on confined resilient modulus of improved lime-soil[J]. Journal of Chang an University(Natural Science Edition), 2013, 33(2):33-37.(in Chinese)( 1) 1) |
| [13] | 杨俊,黎新春,张国栋,等. 风化砂不同掺入率对膨胀土特性影响的研究[J].工业建筑,2013, 43(1):55-60. YANG Jun, LI Xinchun, ZHANG Guodong, et al. Research on the influence on expansive soil characteristics by different mixing rates of weathered sand[J]. Industrial Construction, 2013, 43(1):55-60.(in Chinese)( 1) 1) |
| [14] | 吕大伟,孙晓立. 含水率和压实度对含粘砂土路基回弹模量的影响研究[J].路基工程,2013(3):1-5. LV Dawei, SUN Xiaoli. Study on influence of water content and compactness on resilient modulus of clayey sand subgrade[J]. Subgrade Engineering, 2013(3):1-5.(in Chinese)( 1) 1) |
| [15] | 刘晨辉,张鹏,李清富.聚丙烯纤维水泥稳定碎石抗压回弹模量试验研究[J]. 工业建筑,2008,38(12):96-123. LIU Chenghui, ZHANG Peng, LI Qingfu. Experimental study compressive resilient modulus of polypropylene fiber reinforced cement stabilized macadam[J]. Industrial Construction, 2008, 38(12):96-123.(in Chinese)( 1) 1) |
| [16] | 张翛,赵队家,刘少文,等.美国路基土回弹模量确定方法研究现状[J].重庆交通大学学报(自然科学版),2012,31(4):795-798. ZHANG Xiao, ZHAO Duijia, LIU Shaowen, et al. Research progress on determination of resilient modulus of subgrade soils in U.S.[J]. Journal of Chongqing Jiaotong University(Natural Science), 2012, 31(4):795-798.(in Chinese)( 1) 1) |
 2016, Vol. 39
2016, Vol. 39


