电力系统是生命线工程的重要组成部分，是维持国民经济命脉的关键环节。随着社会经济的发展，各领域对于电力依赖的程度越来越大。近几十年国内外的多次地震灾害对电力设施均造成了巨大破坏，严重影响社会正常的秩序^{[1, 2, 3]}。特高压变电设备通过软母线连接成回路系统后，其整体动力特性较单体设备有较大改变。地震作用下，软母线连接的特高压变电设备自身差异造成变位不同步，使得设备不仅承受自身的地震荷载，还要承受软母线拉压荷载，二者矢量相加后的总荷载可能大于其中任何一个，因此，更容易引起设备损坏。针对软母线连接电气设备的抗震性能，一些研究人员展开了研究分析。Kiureghian等^{[4, 5]}用悬链线描述了软母线的力学特性。Dastous等^[6]对软母线的频率、几何形状、软母线刚度的有限元模拟等进行了研究。谢强等^[7]将软母线简化为索，给出了软母线连接变电站电气设备的数学模型。可以看出：在传统的软母线连接高压电气设备设计中，为了计算方便将软母线的刚度忽略。随着特高压项目的实施，相关变电设备越来越高，柔度越来越大。连接特高压电气设备的软母线往往直径较大而挡距相对较小，这种软母线不但刚度较大而且既抗弯又抗压，在地震作用下软母线的刚度对特高压设备的抗震性能有较大的影响。在这种情况下，忽略软母线刚度的影响无疑会对特高压设备的安全留下隐患。因此，软母线连接的特高压设备抗震计算中应考虑软母线刚度对设备地震响应的影响。笔者给出了考虑软母线刚度的位形函数及最大弧垂，建立了软母线连接的特高压设备有限元模型；并通过振动台试验结果和有限元计算结果的对比分析，验证了该有限元模型的正确性。通过对软母线连接的特高压设备的计算分析，研究了软母线刚度对特高压设备地震响应的影响。笔者的研究成果可为软母线连接的特高压电气设备的抗震设计提供参考。

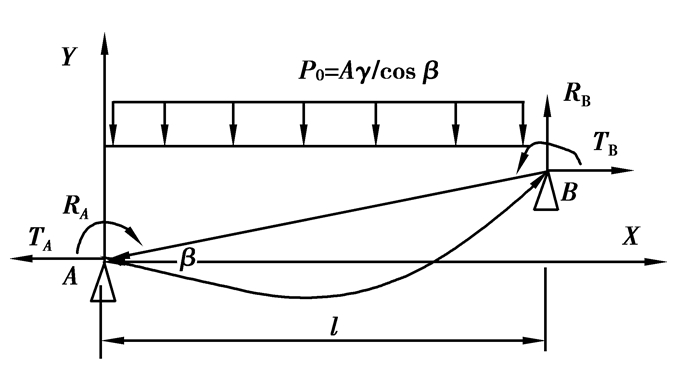
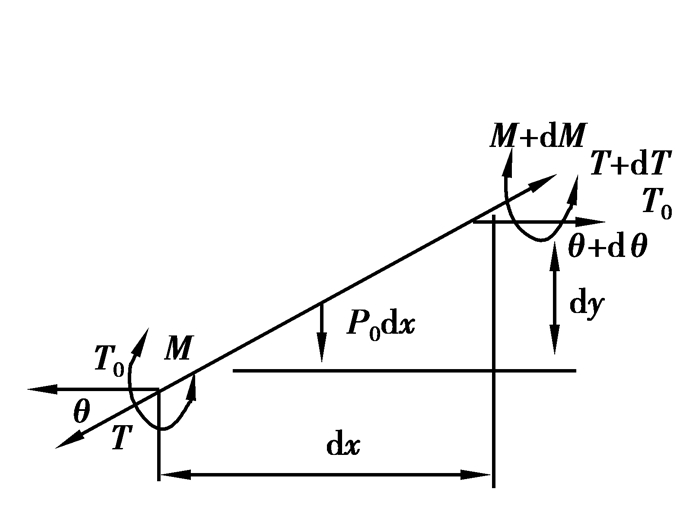
考虑软母线刚度时，软母线的张力方向(如图 1所示)可能与弧垂曲线切线方向不一致。假定软母线单位长度的荷载P=Ar，沿悬挂点连续均匀分布，则单位水平投影长度上的荷载为P₀=Ar/cosβ(N/m)。从图 1中取出微元体(如图 2所示)，T、T+dT和T₀分别为软母线轴向张力、轴向张力增量及水平张力分量(N)。θ为T与T₀间的夹角，M为弯矩(N·m)。

图 1(Figure 1)

图 1 软母线计算简图 Fig. 1 Calculation diagram of flexible bus

图 2(Figure 2)

图 2 软母线微分单元 Fig. 2 Differential element of flexible bus

根据图 2可得平衡方程为

将K²、u代入式(6)得

当x=0时，y=0、$\frac{{dy}}{{dx}} = 0$；当x=l时，y=h，$\frac{{dy}}{{dx}} = 0$；经整理后得

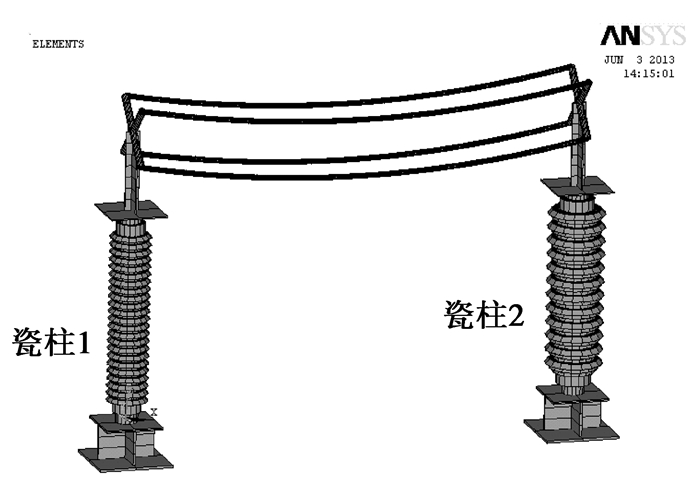
四分裂软母线连接的特高压设备试验模型由特高压瓷柱、四分裂软母线、支座和顶部支架组成。特高压瓷柱顶部用四分裂软母线相连，其连接长度为4 m，垂跨比为1/20。特高压瓷柱底部用法兰盘与支架连接，支架和振动台台面用螺栓相连。瓷柱的设计参数如表 1所示。四分裂软母线直径为0.041 m,弹性摸量为0.66e11 N/mm²,密度为3 213 kg/m³。试验在重庆交通科研设计院桥梁工程结构动力学试验室地震模拟试验台振上完成。台振台面尺寸为3 m×6 m，最大负载35 t，可输入波形包括周期波和随机波等，频率范围为0.1~70 Hz，振动方式为3方向6自由度，该台振性能满足试验要求。根据文献[8, 9, 10]，试验选用了4种激励波：白噪声、标准时程波、天然波1和天然波2，如图 3所示，其中白噪声用来测试四分裂软母线连接的特高压设备试验模型的频率，其他3种波用来测试设备的应变、加速度及位移，输入模拟试验台振激励波的方向为X向。在试验前后，通过输入幅值为0.05 g、持续时间为120 s的白噪声来识别四分裂软母线连接的特高压设备试验模型的频率。通过在特高压瓷柱根部粘贴X方向应变片来测量瓷柱底部X方向应力；通过在特高压瓷柱顶部安装X方向的加速度计和位移计来测量瓷柱顶部X方向的加速度和位移。

图 3(Figure 3)

图 3 输入振动台的波形 Fig. 3 Waveform of input vibration

表 1(Table 1)

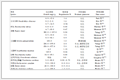
表 1 试件基本参数Table 1 Basic parameters of specimens 设备名称 每节瓷柱长度/m 瓷柱顶截面直径/m 瓷柱底截面直径/m 瓷柱重量/kg 瓷柱1 1.87 0.25 0.25 394 瓷柱2 1.83 0.30 0.30 605

表 1 试件基本参数 Table 1 Basic parameters of specimens

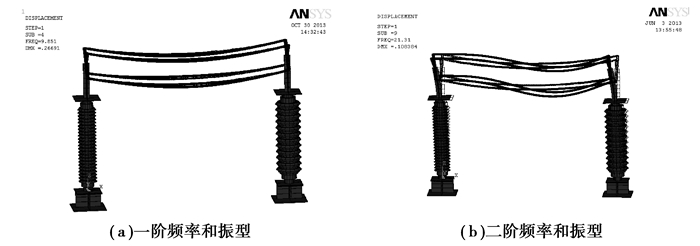
根据四分裂软母线连接的特高压设备试验模型所建立的有限元模型如图 4所示，图中底座、支架、瓷柱用ANSYS中的beam189单元模拟^[11]。四分裂软母线用beam189单元模拟，该单元可模拟软母线的弯曲刚度，软母线的位形函数、最大弧垂可根据式(10)和式(11)建立。由于试验过程中软母线平面外水平加速度和转动加速度都很小,因此，在计算过程中忽略四分裂软母线的水平和扭转刚度的影响。通过对图 5中有限元模型进行计算模态分析和时称分析^{[12, 13, 14]}，四分裂软母线连接特高压模型设备的前两阶振型如图 5所示，其频率如表 2所示；软母线连接的特高压模型设备的顶部最大加速度、顶部最大位移及设备底部最大应变如表 3和表 4所示。可以看出，四分裂软母线具有非线性震荡的特性，计算结果和试验结果比较吻合，从而证明了笔者所建立的考虑软母线刚度的四分裂软母线连接的特高压设备试验模型是正确的。

图 4(Figure 4)

图 4 四分裂软母线连接特高压设备模型有限元模型 Fig. 4 FEA model of the UHV equipment model with four fission flexible bus

图 5(Figure 5)

图 5 四分裂软母线连接特高压设备的频率及振型 Fig. 5 Frequency and mode shape of UHV equipment with four fission flexible bus

表 2(Table 2)

表 2 四分裂软母线连接特高压设备频率Table 2 四分裂软母线连接特高压设备频率 一阶频率/Hz 二阶频率/Hz 试验值 计算值 试验值 计算值 10.74 9.85 19.53 21.33

表 2 四分裂软母线连接特高压设备频率 Table 2 四分裂软母线连接特高压设备频率

表 3(Table 3)

表 3 瓷柱1地震反应实测值与计算值比较表Table 3 Measured values of seismic response of equipment 1 vs calculated values 时程波 顶部加速度/(m·s-2) 顶部位移/mm 底部应力/MPa 试验结果 计算结果 试验结果 计算结果 试验结果 计算结果 标准时程波 (0.8g) 21.90 25.10 3.00 3.16 4.74 4.85 16.46 23.02 2.66 3.37 3.53 4.27 天然波1 (0.4g) 7.35 8.75 1.61 1.24 1.15 1.33 8.13 7.52 0.75 1.63 1.24 1.32 天然波2 (0.4g) 5.86 8.31 0.64 1.22 2.09 2.33 8.83 7.79 1.50 1.67 2.81 2.82

表 3 瓷柱1地震反应实测值与计算值比较表 Table 3 Measured values of seismic response of equipment 1 vs calculated values

表 4(Table 4)

表 4 瓷柱2地震反应试验值与计算值对比Table 4 Measured values of seismic response of equipment 2 vs calculated values 时程波 顶部加速度/(m·s-2) 顶部位移/mm 底部应力/MPa 试验结果 计算结果 试验结果 计算结果 试验结果 计算结果 标准时程波 (0.8g) 19.80 24.35 2.74 3.09 2.57 3.54 18.72 21.14 2.74 3.34 3.46 3.71 天然波1 (0.4g) 6.06 8.11 0.66 1.05 0.89 1.12 7.72 7.32 1.26 1.22 1.34 1.32 天然波2 (0.4g) 5.88 8.19 1.32 1.26 1.39 1.72 7.74 7.80 0.75 1.65 1.02 1.23

表 4 瓷柱2地震反应试验值与计算值对比 Table 4 Measured values of seismic response of equipment 2 vs calculated values

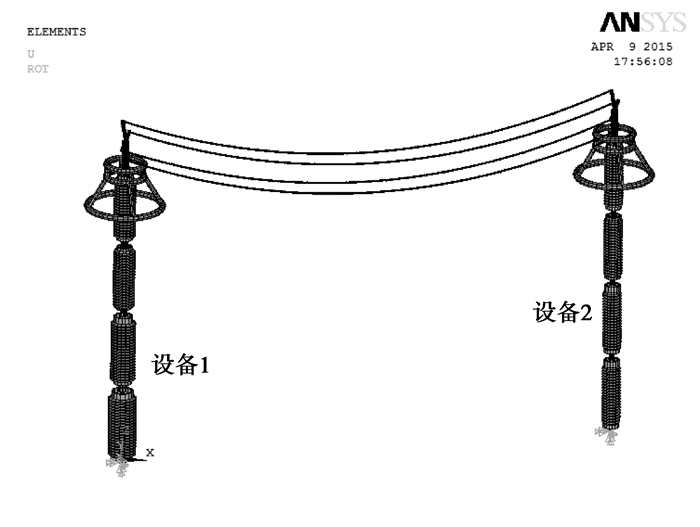
为进一步研究软母线刚度对特高压设备地震反应的影响，笔者建立了软母线连接的特高压设备的有限元模型，如图 6所示。图中设备1为变截面1 100 kV特高压避雷器，高度为11.8 m，瓷套节数为4节，每节瓷套的基本参数见文献[15]。设备2为常截面1 100 kV特高压避雷器，其高度约为11.8 m，瓷套节数为4节，每节瓷套的基本参数如表 5所示。图中的两个特高压避雷器之间的距离为16 m,设备1的基频为2.44 Hz，设备2的基频为1.34 Hz^[16]；四分裂软母线直径为0.041 m,弹性摸量为0.66×10¹¹ N/mm²,密度为3 213 kg/m³;均压环铝管的弹性模量为0.7×10¹¹ MPa、泊松比为0.3、 密度为2 700 kg/m³。输入图 6中有限元模型的时程波为0.24g和0.48g标准波。

图 6(Figure 6)

图 6 四分裂软母线连接的特高压设备有限元模型 Fig. 6 FEA model of the UHV equipment with four fission flexible bus

表 5(Table 5)

表 5 特高压避雷器的基本参数Table 5 Basic parameters of UHV arresters 瓷套内径/mm 瓷套高度/mm 胶装部位外径/mm 胶装部位高度/mm 间隙/mm 重量/kg 400 2 154 500 230 10 942

表 5 特高压避雷器的基本参数 Table 5 Basic parameters of UHV arresters

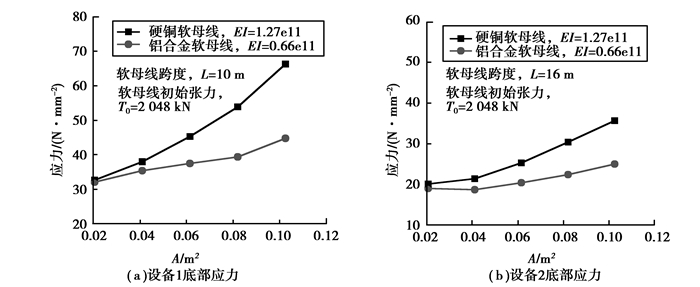
在软母线跨度、垂跨比，初始张力相同的条件下，四分裂软母线连接的特高压设备地震响应如图 7所示。可以看出：当软母线截面面积相同时，弯曲刚度较大的硬铜软母线连接设备的地震响应要明显大于弯曲刚度较小的铝合金软母线连接设备的地震响应。在软母线弹性模量相同的条件下，软母线连接设备的地震响应随着软母线截面面积的增加也随之加大，但硬铜软母线连接设备地震响应随软母线截面面积增加的幅度要明显大于铝合金软母线连接设备的地震响应增加的幅度。这说明随着软母线刚度的增加软母线与设备之间的地震耦合效应也随之增加，从而使设备的地震反应随着软母线刚度的增加而增加。另外，软母线的刚度对其连接设备的影响程度与设备本身的基频有关。从图 7中可以看出，频率较高的设备1的地震响应要大于频率较低的设备2的地震响应，这说明软母线的刚度对频率较高的设备影响较大。

图 7(Figure 7)

图 7 软母线刚度对特高压设备地震反应的影响 Fig. 7 Effect of the stiffness of flexible bus on seismic responses of UHV electrical equipment

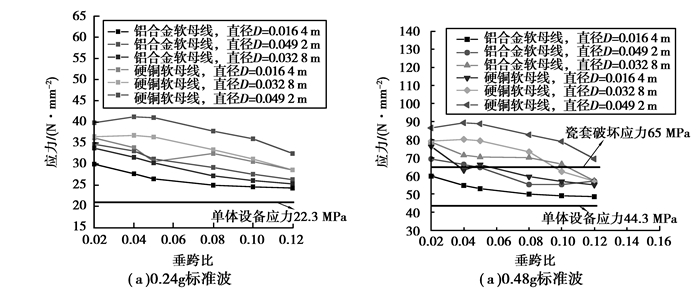
图 8为四分裂软母线连接的设备1瓷套底部应力。可以看出：在0.24g标准时程波的作用下(7度设防地震)，设备1瓷套的底部应力随着软母线垂跨比的降低而增大，其应力大于单体设备的应力。根据式(3)，增加软母线的刚度会使软母线的垂跨比降低，软母线垂跨比的降低会增加软母线和设备之间的地震耦合效应，进而增大高频设备瓷套底部的响应，从而使软母线连接设备的地震反应大于单体设备的地震响应。在0.48g标准时程波的作用下(9度设防地震)，由于软母线刚度的增加，设备与软母线之间存在较强的地震耦合效应，可使设备底瓷套的应力可能超出瓷套的破坏应力而发生破坏。因此，在九度设防的地震作用下，应适当减小软母线刚度以降低软母线和设备之间的地震耦合效应，防止设备在软母线的拉力作用下发生破坏。

图 8(Figure 8)

图 8 特高压设备1瓷套底部应力(MPa) Fig. 8 Bottom stress of UHV equipment 1(MPa)

通过对四分裂软母线连接的特高压设备的理论分析、有限元计算及试验验证得到以下主要结论：

1) 考虑软母线刚度后，软母线连接特高压设备模型的计算结果和试验结果非常相近，说明建立软母线连接的特高压设备的有限元模型时，软母线的位形函数及最大弧垂应考虑刚度的影响。

2) 软母线刚度的增加会增加软母线与设备之间的地震耦合效应，软母线对设备的拉伸作用增强，从而使设备的地震反应随着导线刚度的增加而增加。软母线的刚度对其连接设备的影响程度与设备本身的基频有关，软母线的刚度对频率较高设备的地震反应的影响要大于对设备频率较低设备地震反应的影响。

3) 软母线刚度的增加会降低软母线的垂跨比，而软母线垂跨比的降低会增加软母线和设备之间的地震耦合效应，使软母线连接设备的地震反应大于单体设备的地震反应。在九度设防地震烈度的情况下，由于软母线与设备之间的地震耦合作用较强，应当适当减小软母线刚度并适当增大软母线的最大弧垂，以降低软母线和设备之间的地震耦合作用，防止设备在软母线的拉力作用下发生破坏。