自康普顿散射[1, 2]提出以来,其理论和应用一直是国内外的研究热点。从利用量子理论的微扰论方法计算出散射截面的克莱因仁科公式,到利用量子场论中的重整化理论对康普顿散射的修正。从考虑核对电子的束缚到对康普顿散射理论不断提出近似模型,康普顿散射的应用领域也越来越宽广,甚至把康普顿散射扩展到天体物理、宇宙学以及高能物理领域[3, 4, 5, 6, 7]。研究表明,康普顿散射相对光子数与电子密度成正比[8, 9]。
| $ \Delta N = \Delta V{\varphi _0}{f_1}{f_2}{N_0}\frac{{d{\sigma _{KN}}\left( \theta \right)}}{{d\Omega }}S\left( {q,Z} \right), $ | (1) |
液体和溶液的结构至今还没有被完全认识,当散射体是电解质溶液时,由于分子、离子等的无规则热运动,电解质溶液的结构处于动态平衡,电解质在溶液中,游离态的离子、水分子、水合分子、低水合数水合离子以及高水合数的离子、甚至阴阳离子互相进入对方的第一水合层,进而形成络合物都有可能[10],因此,笔者从宏观上认为溶液中溶质和溶剂的分布是均匀的,电子的分布从宏观上说也是均匀的,而体积元内发生的康普顿散射表现的也是一种平均效应,因此,康普顿散射相对光子数可以反映电子密度的平均效应。其次,与固体散射体相比,液体散射体分子在液体中进行着永不停歇的无规则运动,但是溶液分子无规则的运动速度非常慢,这种无规则运动速率相对于电子本身的运动速率(约为105 m/s)可以忽略。入射光子的能量一般是几十电子伏特至几兆电子伏特,相对于核的能量(质量)来说太小,光子与核的作用一般属于相干散射的范畴,这里可以不考虑。因此,基于式(1),体积ΔV中电解质溶液康普顿散射光子数与浓度x的关系由下式确定[11]:
| $\begin{array}{l} \Delta N = {\varphi _0}{f_c}{f_{1x}}{f_{2x}}{\rho _x}{N_0}\left\{ {x\left[ {\sum\limits_i {{\omega _i}\frac{{{Z_i}}}{{{A_i}}}} } \right] + \left( {1 - x} \right)\left[ {\sum\limits_{i'} {{\omega _{i'}}\frac{{{Z_{i'}}}}{{{A_{i'}}}}} } \right]} \right\}\\ \frac{{d{\sigma _{KN}}\left( \theta \right)}}{{d\Omega }}S\left( {q,Z} \right)\Delta V, \end{array}$ | (2) |
笔者选定NaCl和KCl溶液作为散射体,深入研究了NaCl和KCl溶液康普顿散射。首先从理论上分析适合这两种溶液的康普顿散射光子数与溶液浓度之间的关系,然后通过康普顿散射实验进行验证,并且从微观角度对影响康普顿散射的因素进行了分析。
1 康普顿散射光子数与浓度关系的近似处理鉴于前面的讨论,认为溶液中溶质和溶剂的分布是均匀的,电子的分布从宏观上说也是均匀的,溶液分子无规则的运动速率相对于电子的运动速率可被忽略,对于式(2)确定的容器对光子散射和吸收的补偿因子fc也为常数,溶液的质量密度ρx受浓度的影响情况可以查化学用表[12],如表 1所示,随着浓度的增加,密度近似为线性增加的。
| 表 1 溶液密度ρx、电子数密度与浓度x的关系表 Table 1 The relation among ρx, electron number density, and x |
为了研究方便,设定盛装溶液的容器为圆柱形容器,这是由于如果容器的轴心与载物台中心重合时,射线在入射方向和出射方向走过的距离是对称的(如果其他形状的容器,唯一会有变化的是入射和出射非相干衰减因子不相等,但是不会影响理论推导的结果)。因此,入射和出射方向散射体的非相干衰减因子f1x,f2x相等,可统一为fx,根据文献[13],非相干衰减因子fx与浓度关系由表 2给出。
| 表 2 射线衰减因子fx和KCl、NaCl溶液浓度的关系 Table 2 The relation between fx and KCl, NaCl concentrations |
经过一定的近似处理:综合考虑质量密度(比如常温25 ℃时,浓度为2%、4%、6%、8%、10%、甚至20%的NaCl溶液质量密度分别为1.011 1、1.025 3、1.039 6、1.054 1、1.068 8、1.145 3 g/cm3,几乎是线性变化的)[12]、散射衰减因子(见表 2)、散射体的原子序数和原子量比Z/A的平均值与溶液浓度之间的变化关系(从宏观上看,液体和溶液的分布是均匀的,电子的分布从宏观上说也是均匀的,又由于体积元内发生的康普顿散射也是一种平均效应,为了研究的需要,把对应的 $\frac{Z}{A}$的平均值表示出来即可。对于质量浓度为x的溶液, $\frac{Z}{A}$的平均值可表示为: $\frac{Z}{A} = x\sum\limits_i {{\omega _i}\frac{{{Z_i}}}{{{A_i}}}} + \left( {1 - x} \right)\sum\limits_{i'} {{\omega _{i'}}\frac{{{Z_{i'}}}}{{{A_{i'}}}}} $,其中,第一项表示溶质的 $\frac{Z}{A}$的平均值,第二项表示溶剂的 $\frac{Z}{A}$的平均值,并且浓度在0~0.264之间的小范围内变化,这些因素的综合贡献可以以综合变化关系曲线的切线来替代,在确定的体积ΔV中康普顿散射光子数与溶液浓度的关系最终可以看成是以下线性关系:
| $ \Delta N = \left( {Ax + B} \right)\Delta V, $ | (3) |
| $ A = {f_{C\varphi 0}}{N_0}2a\left( {\sum\limits_i {{\omega _i}\frac{{{Z_i}}}{{{A_i}}}} - \sum\limits_{i'} {{\omega _{i'}}\frac{{{Z_{i'}}}}{{{A_{i'}}}}} } \right)\frac{{d{\sigma _{KN}}\left( \theta \right)}}{{d\Omega }}, $ | (4) |
| $ B = {f_{C\varphi 0}}{N_0}\left( {b\left( {\sum\limits_i {{\omega _i}\frac{{{Z_i}}}{{{A_i}}}} - \sum\limits_{i'} {{\omega _{i'}}\frac{{{Z_{i'}}}}{{{A_{i'}}}}} } \right) + a\left( {\sum\limits_{i'} {{\omega _{i'}}\frac{{{Z_{i'}}}}{{{A_{i'}}}}} } \right)} \right)\frac{{d{\sigma _{KN}}\left( \theta \right)}}{{d\Omega }}, $ | (5) |
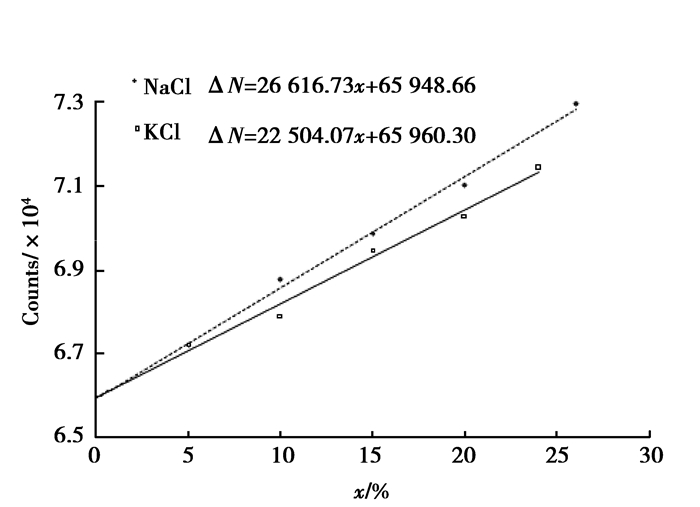
为研究KCl和NaCl溶液的康普顿散射的微观机理,选定在以137Cs 作为放射源的BH-1307型康普顿散射仪上进行实验研究。137Cs放射源能量为661.5 keV,强度为10 mCi左右。一定浓度的溶液80 mL装在直径为20 mm的玻璃容器中,数据采集时间为600 s,散射角为90°和120°。实验时先采集空容器康普顿散射本底,然后采集溶液康普顿散射数据。对所测数据扣除本底以后,利用最小二乘法进行直线拟合后与理论预期一致的结果,拟合后的曲线如图 1、2所示。
|
图 1 散射角90°时NaCl、KCl溶液浓度与康普顿散射相对光子数的关系 Fig. 1 The relation between the scattered photon counts and the concentration of NaCl and KCl solutions at scattered angle 90° |
|
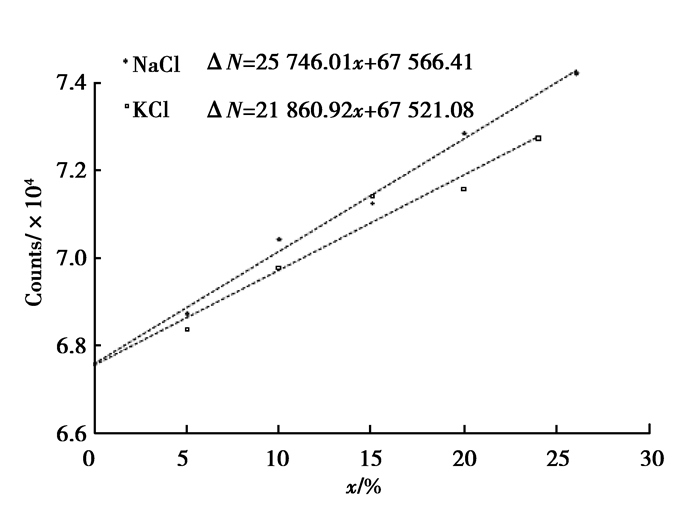
图 2 散射角120°时NaCl、KCl溶液浓度与康普顿散射相对光子数的关系 Fig. 2 The relation between the scattered photon counts and the concentration of NaCl and KCl solutions at scattered angle 120° |
根据图 1、2
KCl溶液浓度与康普顿散射相对光子数的关系为
$ \Delta N = 26{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 616.73x + 65{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 948.66, $
(6)
| $ \Delta N = 22{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 504.07x + 65{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 960.30, $ | (7) |
| $ \Delta N = 25{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 746.01x + 67{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 566.41, $ | (8) |
| $ \Delta N = 21{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 860.92x + 67{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 521.08, $ | (9) |
比较NaCl溶液和KCl溶液康普顿散射数据,可以发现,随着浓度的增加,相同体积康普顿散射光子数增加快慢不一样。从核外电子数的角度,随着浓度的增加,KCl的增加应更快。但事实是,随着浓度的增加NaCl的康普顿散射光子数增加更快。另外,在这两种溶液中,Na相对于K而言算是较轻的元素,它的康普顿散射更符合康普顿散射的规律。同时,从表 1和2看出质量密度、衰减因子对康普顿散射的影响是不明显的。但是从实验结果看,康普顿散射光子数与浓度之间的关系比较明显。因此,笔者认为要从更微观的角度,从散射体的电子结构方面来分析,才能真正揭示康普顿散射更本质的机理。
3 NaCl和KCl溶液的电子结构分析 3.1 电子数密度由式(1)可知,当溶液的浓度增加时,离子的电子数密度随着增加,而散射相对光子数与单位体积内的电子数是成正比的。这说明,当溶液的浓度增加时,溶液中发生康普顿散射的次数将会增加。因此,电子数密度对康普顿散射的影响是很大的。笔者首先分析了散射体的电子数密度。由表 1知,在NaCl和KCl溶液中,随着浓度的升高,电子数密度也随着增加,这一点与实验吻合得很好。另外,从增加的幅度上看,KCl溶液浓度每增加2%,电子数密度增加的幅度约为0.020×1029/m3,而NaCl溶液浓度每增加2%,电子数密度增加的幅度约为0.039×1029/m3,浓度从2%到10%电子数密度的总增加量也有很大差别:KCl电子数密度增加的总幅度约在0.081 7×1029/m3,而NaCl电子数密度增加的总幅度约为0.154 4×1029/m3,因此,从电子数密度角度可以看出,与KCl溶液相比较,由于NaCl溶液随着浓度的增加电子数密度增加更快,参与康普顿散射的电子数也随着浓度增加而增加得更快,因此,接收到的康普顿散射光子数就会增加得更快,在图 1和2中,NaCl溶液康普顿散射的直线斜率更大,与这一规律是相一致的。不过,如果仅仅是电子数密度影响康普顿散射光子数,由于NaCl电子数密度增加的幅度基本上是KCl电子数密度增加的幅度的2倍,如果没有其他因素的影响,直线斜率的差距应该也约为2倍,但是由图像还可看出,斜率间的差别并没有预想得大,这意味着除了电子数密度这个主要因素的影响之外,还有其他因素影响康普顿散射。
3.2 射线衰减因子对康普顿散射的影响由表 2可知,随着溶液浓度的增加,射线衰减因子随之增加,虽然根据式(2)可知,康普顿散射光子数与入射射线衰减因子和出射射线衰减因子的乘积成正比,但是增加幅度非常小。而就KCl、NaCl溶液射线衰减因子相比较,也可以看出,两散射体几乎没有什么差别。因此,在康普顿散射光子数的影响因素中也只是一个次要的因素。
3.3 水分子与离子数比根据实用化学手册[12]可知,NaCl和KCl溶液在标准大气压下的溶解度分别为36 g/100 cm3和34 g/100 cm3,可以得出饱和溶液的浓度分别为26.47%和25.37%。根据文献[12]提供的数据也容易算出不同浓度的NaCl溶液和KCl溶液中水分子与离子个数之比,如表 3所示,由于溶质分子溶解到水溶液中形成离子时会形成水合离子,对于一定浓度的溶液,游离态的离子、游离态的水分子、水合分子、低水合数的水合离子和高水合数的水合离子都是存在的且处于一个动态平衡中,由表 3中数据可知随着溶液浓度的升高,NaCl和KCl的水分子个数在减少,水分子数与离子数之比在减少。因此可以认为,随着溶液浓度的升高,Na+、K+、Cl-的水合数在减少。文献[14, 15]显示在极稀的溶液中K+、Na+、Cl-水合数理论值分别是8、6和6。因此,在不够稀的溶液中离子形成水合离子时,其水合数应该比上述理论值要小。而且,溶液中游离态的离子、游离态的水分子、水合分子、低水合数的水合离子和高水合数的水合离子在溶液中所占的比例与溶液浓度有关,浓度低时,高水合数的水合离子相对多,而低水合数的水合离子以及游离态的离子相对更少,浓度高时,低水合数的水合离子以及游离态的离子相对更多,高水合数的水合离子相对更少。在康普顿散射中,按散射体的这种情况,康普顿散射光子数肯定要受影响。下文从溶液散射体微观层次的电子结构分析NaCl和KCl溶液康普顿散射的有关影响因素。
| 表 3 不同浓度的NaCl、KCl溶液水分子与离子个数之比(以100 g溶液计) Table 3 The ratio of aqueous water molecule numbers and ion numbers of different concentrations |
为了分析电子结构影响,利用密度泛函理论(DFT)方法计算了各散射体的详细电子结构[16, 17, 18]。密度泛函理论是量子力学计算方法,是物理、化学和材料科学研究最常采用的研究方法。因为它不依赖于任何经验参数,它提供了高精度和预测能力。笔者应用量子化学计算软件,使用拟合电荷的ESP(the electrostatic potential)分析法,导出电荷分布的相关属性,考虑到计算机的性能限制,选择高精度(fine),选择水作为溶剂,其介电常数为78.4,对于溶剂化效应COSMO中的其他参数,则采用默认值。
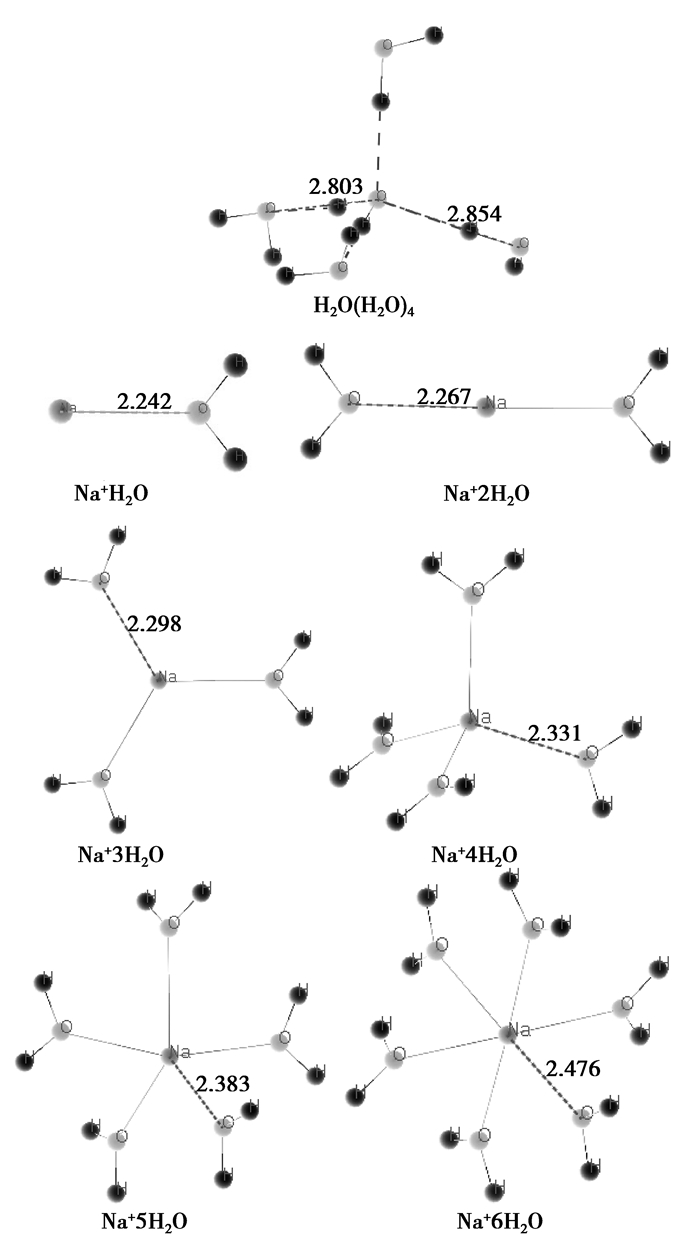
根据前面分析,随着浓度的升高,低水合数的离子以及游离态的离子会越来越多,高水合数的离子会越来越少。因此,假定水合数的多少对应溶液浓度的高低,也即浓度高的,其离子的水合数少;而浓度低的对应的水合数多。对NaCl溶液和KCl溶液的水合离子结构进行优化后,结果如图 3~5所示。
|
图 3 优化后的水合钠离子和H2O(H2O)4 Fig. 3 The structure of Na+ hydrate and H2O(H2O)4 after optimization |
|
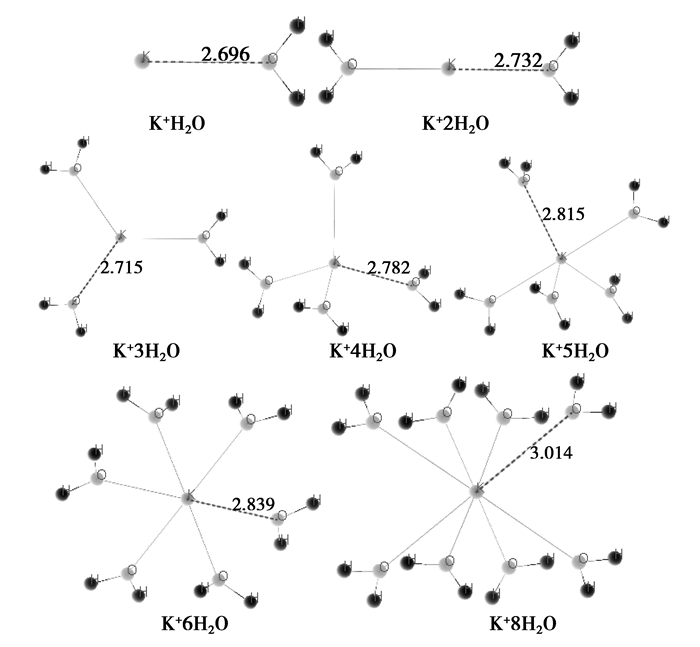
图 4 优化后的水合钾离子 Fig. 4 The structure of K+ hydrate after optimization |

|
图 5 优化后的水合氯离子 Fig. 5 The structure of Cl- hydrate after optimization |
比较认同的水的结构是通过不同水分子间的氢键构成四面体结构,其中一个水分子处在四面体的中心,其余4个水分子分别处于四面体的4个顶点。而在NaCl和KCl溶液中,由于Na+、K+、Cl-的介入,打破了水的这种结构,同时与水分子结合构成水合离子,并且都处于各自水合物的中心,对于Na+、K+,水分子与中心原子是通过水分子提供孤对电子、中心原子提供空轨道进行结合的;而对于Cl-,水分子与中心Cl-是通过水分子中的H提供空轨道、中心原子提供孤对电子进行结合的。由于低水合数的水合离子对应于高浓度,研究组基于第一性原理计算了这些水合离子的等效电荷的分配情况,如表 4所示。
| 表 4 水合Na+、K+和Cl-的等效电荷(单位:正电子电荷量) Table 4 The equivalent charge distribution table of the Na+、 K+ and Cl- hydrate(e) |
对于极稀的溶液,有文献知Na+、K+、Cl-的水合数理论上的值分别是6、8、6。因此,上述计算中,Na+6H2O、K+8H2O、Cl-6H2O应该是最稳定的,与理论上的最为一致。根据表 5,可以看出如下规律:
1) 水合Na+水合数越少(浓度越高),Na+等效电荷就越小,说明电子偏离Na+,Na+对电子的束缚就越弱;而对于O,这种规律性不明显(笔者认为,这种规律之所以不明显,这是因为对于水合数为奇数的水合离子,稳定性差,很容易受到其他分子的影响。比如Na+3H2O,如果要保持对称性,只能是平面结构,但这种平面的两侧最容易受到其他分子或离子的干扰),但整体是随着水合数的降低,O等效电荷也随着降低,说明低水合数的水合离子中,电子受到的束缚也是越来越弱的。
2) 水合K+水合数越少(浓度越高),K+ 等效电荷就越小,说明电子偏离K+,Na+对电子的束缚就越弱;而对于O,这种规律性没有那么明显,但整体是随着水合数降低,O等效电荷也随着降低,说明低水合数的水合离子中,电子受到的束缚也是越来越弱的。
3) 与Na+、K+规律相反,水合Cl-水合数越少(浓度越高),Cl- 等效电荷就越大,说明电子偏向Cl-,Cl-对电子的束缚就越强;而对于水合Cl-中的O,这种规律性不明显,但是O的有效电荷数有下降趋势。说明对电子的约束其主要作用的是Cl-。
4) 水合Na+和水合K+水合数越少(浓度越高),对应的等效电荷就越小,Na+和K+对电子的束缚就越弱。由表 5还可以进一步得出,随着水合离子水合数的增加,Na+和K+的等效电荷变化幅度也不一样,对于Na+来说,由Na+H2O到Na+6H2O,等效电荷增加了0.787e,而对于K+,由K+H2O到K+6H2O(为使数据具有可比性,故选择K+6H2O进行比较),等效电荷增加了0.515e,考虑到Na+的尺度比K+的尺度小,可知就电子受到的约束而言,水合Na+的电子受到的约束较K+的大。
总之,水合离子由于水合数减小导致各原子和离子的等效电荷呈现一定的规律性,导致水合离子中电子受到的约束也呈现规律性变化。而对于康普顿散射,电子受到约束越大,散射发生的几率越小,导致接收到的康普顿散射光子数减少[19, 20, 21]。因此,仅仅考虑电子受到的约束这一因素,可知NaCl与KCl溶液康普顿散射的散射光子数随着浓度增加而增加,且KCl溶液的增加要快一点。
4 结 语基于康普顿散射的理论和实验研究,立足于密度泛函理论对NaCl与KCl溶液的电子结构作了深入分析,得出除质量密度、散射衰减因子以及溶液的浓度对康普顿散射光子数有影响外,电子数密度和电子受到的束缚也对康普顿散射光子数有影响。从随溶液浓度的变化电子数密度的变化规律可以看出,NaCl与KCl溶液康普顿散射的散射光子数随浓度增加而增加。而通过对NaCl与KCl溶液电子结构的进一步分析,得出仅考虑电子受到的约束这一因素,可知NaCl与KCl溶液康普顿散射的散射光子数随着浓度增加而增加,且KCl溶液的增加要快一点。
| [1] | COMPTON A H. A quantum theory of the scattering of X-rays by light elements[J]. Physical Review, 1923, 21, 483-502.( 1) 1) |
| [2] | VENUGOPAL V, BHAGDIKAR P S. Broglie Wavelength and Frequency of the Scattered Electrons in Compton Effect[J]. Physics Education, 2012, 29(1):35.( 1) 1) |
| [3] | ROLAND Currat, DECICCO P D, WEISS R J. Impulse Approximation in Compton Scattering[J]. Physical Review B, 1971(4):4256-4261.( 1) 1) |
| [4] | RAO D V, SELTZER S M, BERGSTROM, P M Jr. Compton scattering cross-sections for individual subshells for a few elements of biological interest in the energy region 5 keV-10 MeV[J]. Radiation Physics and Chemistry,2004,70(4/5):479-489.( 1) 1) |
| [5] | MARTIN Schumacher. Studies on the electromagnetic structure of the nucleon by free and quasi-free Compton scattering at MAMI (Mainz)[J]. Nuclear Physics A, 2002, 721(16):773-776.( 1) 1) |
| [6] | CLAUDIO Coriano, ANATOLY Radyushkin, GEORGE Sterman.QCD Sum Rules and Compton Scattering[J]. Nuclear Physics, 1993(405):481-506.( 1) 1) |
| [7] | PASQUINUCCI A, PETRINI M. On the Compton Scattering in String Theory[J]. Physics Letters B, 1997,414(3/4):288-296.( 1) 1) |
| [8] | Sharaf J M. Practical aspects of Compton scatter densitometry[J]. Appl. Radiat. Isot, 2001, 54:801-809.( 1) 1) |
| [9] | LUO Guang,HU Xianquan. Theory and experiment on Compton scattering of binary powder mixture[J]. Journal of Chongqing University(English Edition),2010,9(1):29-34.( 1) 1) |
| [10] | J.伯吉斯.祝振鑫,向家忠.溶液中的离子[M].译.北京:原子能出版社,1987:4-7. Burgess J, ZHU Zhenxin, XIANG jiazhong. Ion in soulution[M].Trans. Beijing:Atom Energy Press, 1987:4-7.(in Chinese)( 1) 1) |
| [11] | LUO G, ZHOU S Q, HAN Z,et al. Relationship between scattered photon counts and concentrations of some saline solutions in Compton scattering[J]. Chinese Journal of Chemistry, 2007(2):164-167.( 1) 1) |
| [12] | 张向宇.实用化学手册[M].北京:国防工业出版社,1986. ZHANG Xiangyu. Handbook of Applied Chemistry[M].Beijing:National Defense Industry Press,1986.(in Chinese)( 1) 1) |
| [13] | HUBBELL, J H. Photon Cross Sections, Attenuation Coefficients and Energy Absorption Coefficients from 10 keV to 100 GeV[M]. U. S. National Bureau of Standards,1969.( 1) 1) |
| [14] | SKIPPER N T, CUMMINGS S C, Neilson G W, et al. Ionic structure in aqueous electrolyte solution by the difference method of X-ray diffraction[J]. Education Medica, 2004, 7(2):70-72.( 1) 1) |
| [15] | OHTOMO N, ARAKAWA K. Neutron diffraction study of aqueous ionic solutions. I Aqueous solutions of sodium chloride and potassium chloride[J]. Bulletin of Chemical Society of Japan, 1980, 53 (7):1789-1794.( 1) 1) |
| [16] | SEGALL M D, LINDAN P J. First-principles simulation:ideas, illustrations and the CASTEP code[J]. Journal of Physics:Condensed Matter,2002, 14(11):2717.( 1) 1) |
| [17] | BURKE K, WERSCHNIK J, GROSS, E K U. Time-dependent density functional theory:Past, present, and future[J]. The Journal of Chemical Physics, 2005,123(6):62-206.( 1) 1) |
| [18] | KOHN W, SHAM L J. Self-Consistent Equations Including Exchange and Correlation Effects[J]. Physical Review,1965, 140 (4A):1133-1138.( 1) 1) |
| [19] | EAST L V, LEWIS E R. Compton scattering by bound electrons[J]. Physica, 1969, 11(44):595-613.( 1) 1) |
| [20] | BERGSTROM P M Jr. SURIC T. PISK K, et al. Compton scattering of photons from bound electrons:Full relativistic independent-particle-approximation calculations[J]. Clinical Microbiology & Infection, 1993, 48(2):44-49.( 1) 1) |
| [21] | RIBBERFORS R. Relationship of the relativistic compton cross section to the momentum distribution of bound electron states[J]. Physical Review B (Solid State), 1975, 15(12):2067-2074.( 1) 1) |
 2016, Vol. 39
2016, Vol. 39

