随着经济的快速发展，能源供应紧张、环境污染等现象日益严重，可再生无污染的风能成为了未来能源的重要支柱之一。风力发电机制造和维修成本极其昂贵，诸多风场均发生过批次性更换齿轮箱的事件，耗费资金均在百万级以上，因此高可靠性成为齿轮箱极其重要的指标。齿轮箱中的行星架是传扭的重要部件，但其中存在着一些不确定参数，使得行星架的强度也具有一定的分散性，因此传统的安全系数并不能全面反映行星架的可靠度，必须借助可靠性分析来评价齿轮箱的可靠度^{[1, 2]}，在此基础上进行结构的参数优化，就能比较全面地提高行星架可靠度。

响应面法是用多元多项式或非多项式模型(如kriging模型)来描述系统自变量和响应特征的复杂关系，从而替代有限元仿真和其它复杂模型进行更有效设计或计算的一种方法^{[3, 4]}。响应面法源自统计计量经济学，在结构的参数优化与分析应用方面也逐渐成熟，郭勤涛等对响应面法的样本点选取、响应面拟合做了比较全面的描述^{[3, 4]}。费庆国等对显著性参数筛选的方差分析方法做了比较深入的研究^[5]。因此，响应面法应用也逐渐成熟，在可靠性设计中，蒙特卡洛模拟对系统无具体数学模型或模型比较难描述的问题特别有效，能够通过参数的抽样点，计算出特征量响应值，并通过概率统计的概率密度、累计概率密度、正态分布校验等方法来识别特征量的统计特性，以此研究系统的特性。蒙特卡洛法是比较成熟的计算方法，但高精度的响应值必须取大量的样本点，通常都在百万级左右，这样的计算量如果都是基于有限元模型进行计算，是不可能完成的，所以文中采用了快速的响应面模型，就解决了计算量的问题。

快速响应面模型能够直接替代有限元计算，使得大规模工程问题求解时间大大缩短，非常适用于结构参数优化及可靠性设计。其基本思想是通过确定性试验设计拟合一个响应面函数来模拟真实的输入和输出之间的隐式关系，使系统的进一步分析可以建立在响应面函数上，采用快速响应面模型目的在于研究特征量的统计特性时能极大地提高计算效率。多项式回归分析是建立响应面模型的核心，其具体可分为如下几个部分。

基于回归分析的响应面拟合是对样本数据进行操作，常用的试验设计方法为全因子试验设计、中心点复合设计、box-behnken design、D-最优设计等^{[5, 6]}。

D-最优设计定义如下，研究回归模型为

应用F值检验法进行假设检验，找出显著性参数定为主参数。例如，有限元模型的设计参数A，对其某一响应特征(比如模态频率f)的F检验如下

系统的特征量y为因变量，x_i(i=1,2,…,k)代表k个设计参数，采用一阶交互项和二次项的响应面函数可表示为

蒙特卡洛法亦称随机模拟法，通过随机数试验，求得特征量的近似解，尤其对系统无具体数学模型或模型比较难描述的问题特别有效。

蒙特卡洛法的基本思路是首先确定概率模型，即所求问题的解为概率模型的特征量，通过蒙特卡洛抽样获取大量的样本点，求解特征量的值，并采用统计分析手段对特征量的特性进行分析。蒙特卡洛法关键是抽样，常见抽样方法有直接抽样，超拉丁抽样、中心点复合抽样等，其中超拉丁抽样具有避免样本点重复与集中地性质而广泛应用。相比较直接抽样法，超拉丁抽样能够缩减20%~40%计算规模，且能够达到同样的计算精度，如图 1所示。

图 1(Figure 1)

图 1 二参数超拉丁样本点分布 Fig. 1 Two paramters sampling of Latin Hypercube Sampling

可靠度是指应力超过强度的概率，已知正态分布x_s、x_σ，令δ=x_s－x_σ，f(δ)也服从正态分布^{[8, 9]}

令 $t = \frac{{\delta - \bar \delta }}{{{S_\delta }}}$，则dδ=S_δdt，

当δ=0，t=-${\bar \delta }$/S_δ；当${\bar \delta }$=∞，t=∞，转换为标准正态分布函数

因此，应力和强度联接起来，亦称“联接方程”，Z称为联接系数。然后依据正态分布表查阅处所需可靠度R。

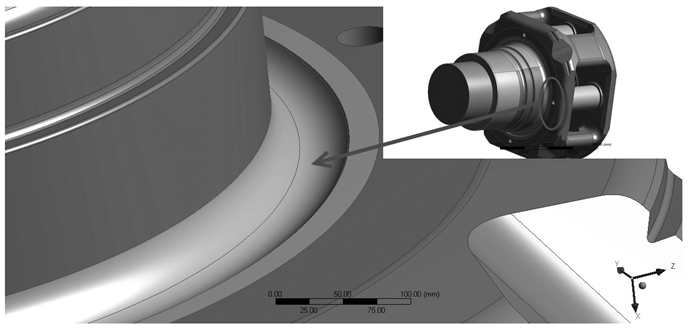
在GL旋转坐标系下，行星架主要承受从轮毂中心传递来的扭矩与弯矩。根据经验，行星架静强度最薄弱环节主要为前轴承座清根处(如图 2所示)，立柱倒角处以及内部油孔等，而弯矩传递至前轴承比后轴承大很多，因此取前轴承座清根处为研究对象具有重要意义。模型与材料参数见表 1。

图 2(Figure 2)

图 2 行星架前轴承座清根(圈出位置) Fig. 2 The relief cut of planet carrier

表 1(Table 1)

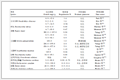
表 1 模型与材料Table 1 Material 行星架材料 主轴与销轴 材料 GJS700 42CrMoA 杨氏模量/GPa 176 206 泊松比 0.275 0.3 屈服强度/MPa 230 — 单元数 78万 24万 单元类型 Solid186/187 Solid186/187 连接方式 frictional

表 1 模型与材料 Table 1 Material

约束主轴末端，扭矩传递至行星轮并转换为轴承载荷，弯矩传递至前后轴承并转换为轴承载荷，同时考虑收缩盘压力，如图 3所示，载荷参数见表 2。

图 3(Figure 3)

图 3 约束、载荷与网格 Fig. 3 Constraints, loads & meshing

表 2(Table 2)

表 2 载荷Table 2 Load 名称 主轴承处 扭矩Mx/kN·m 2 519.9 弯矩My/ kN·m 1 297 弯矩Mz/kN·m 175

表 2 载荷 Table 2 Load

行星架的设计、生产与装配过程中存在着诸多不确定性参数，这些参数会对行星架强度有一定影响，描述见表 3。

表 3(Table 3)

表 3 不确定性参数Table 3 Uncertain parameters 编号 名称 描述 1 铸造圆角公差 反映内孔壁厚变化量 2 过盈量 叶片侧销轴过盈量 3 材料力学性能 采购件力学性具有分散性 4 零件最大厚度 零件屈服强度与厚度有关 5 铸造腹板偏差度公差 行星架前后腹板偏差量 6 铸造立柱厚度公差 大多为变半径设计

表 3 不确定性参数 Table 3 Uncertain parameters

由于缺乏数据，暂不研究材料力学性能和零件最大厚度，只研究过盈量与铸造公差这两类参数的影响。依据现有数据，取图 4~图 7中4个不确定性参数作为研究的对象。

图 4(Figure 4)

图 4 铸造圆角R1 Fig. 4 Casting rounding R1

图 5(Figure 5)

图 5 铸造过渡圆角R2 Fig. 5 Casting rounding R2

图 6(Figure 6)

图 6 前后腹板偏差 Fig. 6 Casting tolerance of front and rear plate

图 7(Figure 7)

图 7 叶片侧销轴过盈量 Fig. 7 Assemble interference fit of front hole of carrier

取前后腹板偏差为随机变量；铸造圆角R1取草绘图中圆角半径为随机变量，其余取原始值。

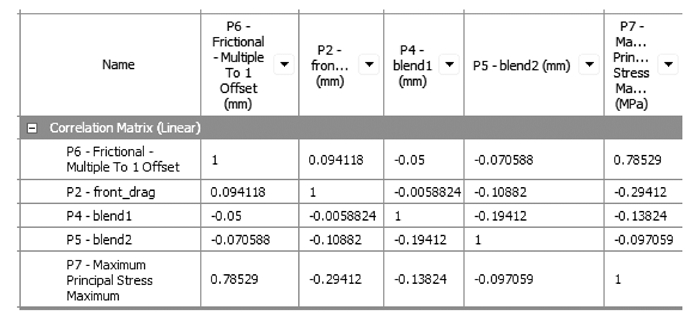
首先对4个随机变量进行归一化，使抽样更为简便，采用D-最优法取样本点60组，代入参数化后的有限元精细模型进行计算，得到清根处拉应力值。相关性矩阵如图 8所示。

图 8(Figure 8)

图 8 相关性矩阵 Fig. 8 Correlation matrix

表 4(Table 4)

表 4 参数与分布Table 4 Normal distribution 编号 描述 正态分布 P4 铸造圆角R1 N(20,1) P1 铸造过渡圆角R2 N(55,1) P2 前后腹板偏差 N(1,0.05) P6 过盈量 N(0.028,0.001 4)

表 4 参数与分布 Table 4 Normal distribution

表 5(Table 5)

表 5 显著性参数 Table 5 Dominant sensible parameters 编号 显著性 P4 ★ P1 — P2 ★★ P6 ★★★★

表 5 显著性参数 Table 5 Dominant sensible parameters

通过方差分析发现铸造过渡圆角R1对清根处强度几乎无影响，因此忽略。取剩余3参数为研究对象，进行独立性与相关性分析，通过相关矩阵可以发现3个随机变量表现为弱相关性。

取这3个随机变量为参数，采用D-最优法取样35样本点，代入参数化后的有限元精细模型计算清根处拉应力。归一化后样本点组合如图 9所示，整个取样点由MATLAB编写的程序完成。

图 9(Figure 9)

图 9 归一化样本点 Fig. 9 Normalization sampling points

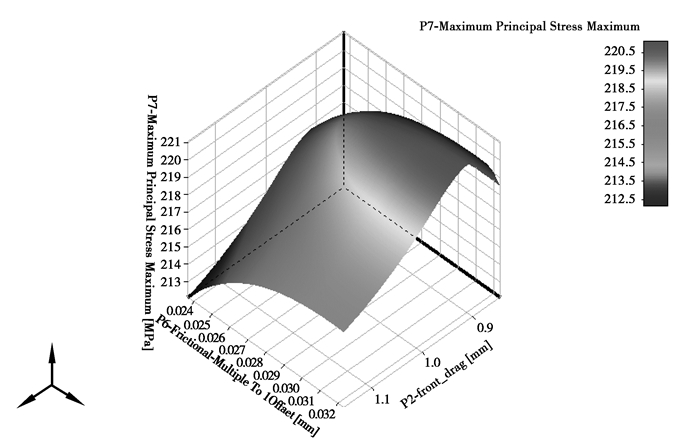
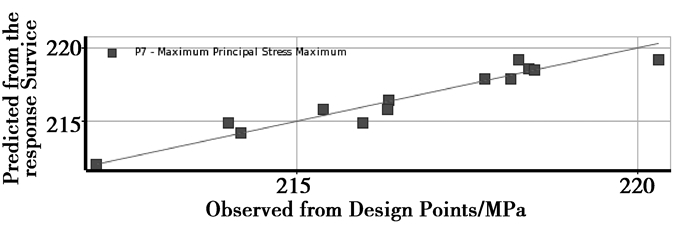
取三阶多项式模型(包含二阶交互项)进行回归拟合。根据经验，在结构静强度计算中，响应和参数的非线性程度不强，因此三阶多项式模型精度已经较高，能够满足计算要求。通过最小二乘估计，求解出多项式的系数。各响应面如图 10~图 12所示，响应面精度校验见表 6。

图 10(Figure 10)

图 10 S1关于腹板偏差和过盈量响应面 Fig. 10 S1 response surf of plate tolerance and interference fit

图 11(Figure 11)

图 11 S1关于倒角R1和过盈量响应面 Fig. 11 S1 response surf of rounding R1 and interference fit

图 12(Figure 12)

图 12 S1关于倒角R1和腹板偏差响应面 Fig. 12 S1 response surf of plate tolerance and rounding R1

表 6(Table 6)

表 6 响应面精度校验Table 6 The prediction accuracy 编号 RSME R2 取样点 0.59 0.27 新样本点 0.90 0.59

表 6 响应面精度校验 Table 6 The prediction accuracy

同时，响应面除了对拟合点的预测精度较高外，还必须对非拟合点的预测精度也一样高，这样的响应面才具有较高可信度。随机取8个单独的样本点，对比响应面预测值与有限元计算值。响应面可信度符合要求(如图 13~图 14所示)。

图 13(Figure 13)

图 13 样本点与拟合预测点一致性 Fig. 13 Prediction and real sampling result comparison

图 14(Figure 14)

图 14 样本点与非拟合预测点一致性 Fig. 14 Prediction and un-sampled point result comparison

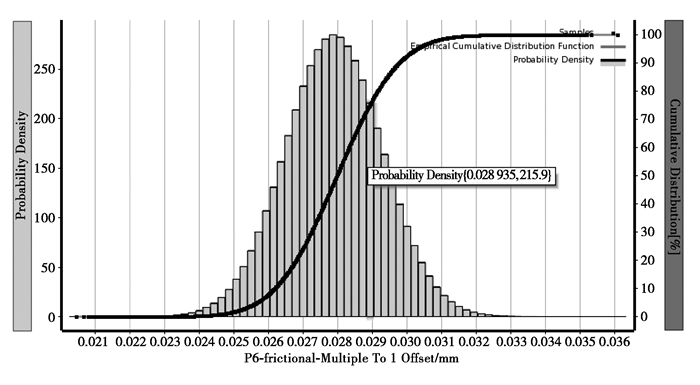
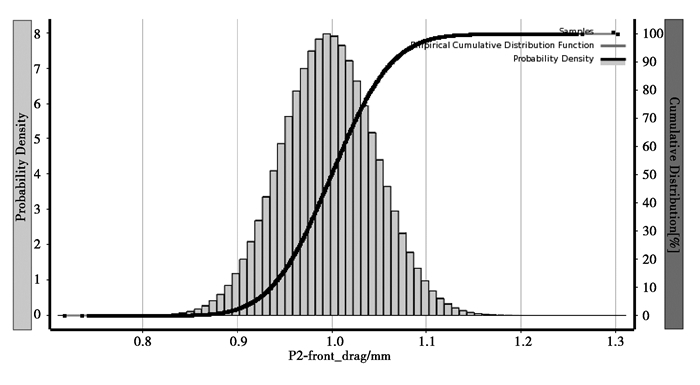
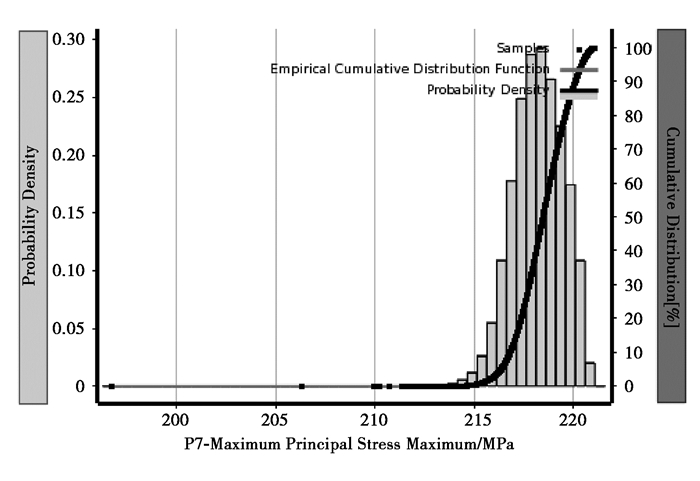
文中抽取3参数组合样本点100万，通过超拉丁方抽样法获取样本点，样本点绘图如图 15~图 18所示，柱状图为概率密度，黑线为累计概率密度。

图 15(Figure 15)

图 15 过盈量抽样累计概率密度分布 Fig. 15 Accumulate probability of interference fit

图 16(Figure 16)

图 16 腹板偏差样累计概率密度分布 Fig. 16 Accumulate probability of plate tolerance

图 17(Figure 17)

图 17 圆角R1抽样累计概率密度分布 Fig. 17 Accumulate probability of rounding R1

图 18(Figure 18)

图 18 特征量S1累计概率密度分布 Fig. 18 Accumulate probability of response S1

在GL和IEC认证规范^{[11, 12]}中，考虑了材料强度安全系数、载荷安全系数以及其他安全系数，因此安全系数较高。如下计算都是已经考虑了这些折现系数之后的结果。

在不考虑不确定性参数时，计算

1) 不确定性参数对行星架强度的影响比较明显，应着重考虑不确定性参数均值影响，显著性参数过盈量和前后腹板偏差对清根处强度影响明显；

2) 在已考虑认证规范安全系数后，行星架可靠度仍可达99.324%，表明行星架静强度可靠度很高，因此可靠度分析能够比较全面直观地反映行星架的安全裕度；

3) 响应面法是不确定性参数分析的有效方法，而蒙特卡洛模拟是随机参数研究的有效手段，在文中研究基础上，后续可进行高精度响应面法研究以及参数优化。