2. 山东科技大学 电气信息系, 济南 250000
2. Department of Electrical Information, Shandong University of Science and Technology, Jinan 250000, P. R. China
城市交通的供需不平致使交通拥堵问题日益严重。智能交通系统(intelligent traffic system, ITS)是解决交通拥堵问题,提高道路通行能力的有效途径。使用ITS对交通流进行控制和诱导的前提是实现对交通流状态的实时预测。
近年来,许多研究者对短时交通流预测进行了研究,并取得了一系列的研究成果。其中大部分研究使用传统统计方法及浅层的机器学习模型。2003年,Williams等[1]使用自回归积分滑动平均(autoregressive integrated moving average, ARIMA)对交通流量进行了预测。2002年,Smith等[2]使用ARIMA模型对交通流序列进行建模,证明了ARIMA模型的预测效果优于一些非参数模型。2016年,Hu等[3]使用粒子群优化(partical swarm optimization, PSO)算法对支持向量回归机(support vector regression, SVR)的参数进行优化,并将优化后的SVR模型用于短时交通流预测,证明了优化模型比现有预测算法的误差更小。随着交通大数据的剧增,及交通流数据具备多维度、非线性等问题日益突出,研究者尝试运用深度学习的方法,使用非线性模型对交通流数据进行分析[4-6]。2015年,Ma等[7]将长短期记忆网络(long short-term memory, LSTM)用于预测交通流预测,实验证明相较于其他模型,LSTM可以有效地捕捉交通流的非线性状态及车辆行进过程中速度的突然变化。2016年,Fu等[8]将门循环单元(gate recurrent unit, GRU)用于交通流量的预测,证明了基于深度学习的非线性算法的性能优于传统的线性算法。
近年来大部分交通流预测模型都是针对交通流序列的单步预测建立的,只适用于ITS短期决策问题中,例如交叉口的信号配时。为满足ITS对于道路拥堵形成时间、路径规划等问题的决策,还需要对交通序列做多步预测。使用单一的神经网络模型对较长的序列进行多步预测时,每一步的预测误差将会随着预测步长的增加而增加,从而使预测得到的序列与原始序列存在较大的偏差[9-11]。
为解决这一问题,文中将自然语言处理领域表现出色的编码器解码器(encoder-decoder, ED)结构应用于交通流预测的任务之中。编码器将历史的交通流序列信息压缩为一个固定维度的状态向量,解码器对该状态向量进行解析,通过递归方式将预测结果反馈到网络中,以此减缓误差随着预测补偿的迅速累积,实现更为准确的多步预测。
除此之外,交通流因受交通流量、速度、时间占有率、密度等因素的影响,往往呈现出非线性的特点[12-16]。因此,对交通流进行有效预测要使模型能够充分挖掘交通流序列中多个变量之间的非线性关系。LSTM能够对传感器数据的时间序列,及固定长度、固定周期的信号数据的显著特征进行有效的学习。
基于此,文中提出基于LSTM的Encoder-Decoder多步交通流预测模型(encoder-decoder LSTM multi-step traffic flow prediction model, ED LSTM),实现端到端的交通流序列预测。主要的贡献点:
1) 使用Encoder-Decoder学习框架,通过一个LSTM编码器,将交通流序列中的时间特征编码为上下文向量,使用另一个LSTM作为解码器,对向量做解码,并进行预测。
2) 使用LSTM提取多变量交通流序列中的深层表达能力,提高了预测的准确性。
3) 基于2个真实的交通数据集进行实验,实验结果表明,ED LSTM模型在单变量、多变量输入的多步交通流预测中任务中均具有良好的预测能力,并且优于对照组模型。
1 相关技术在模型的搭建中,使用ED结构搭建深度学习模型,LSTM作为编码器和解码器,并对所用到的ED结构、LSTM等基础知识进行简单介绍。
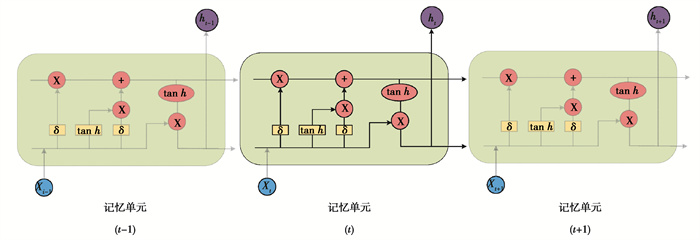
1.1 LSTM模型LSTM是时间循环神经网络的一种,通过在循环神经网络(recurrent neural network,RNN)的基础上增加门控(输入门、遗忘门和输出门)以确定信息的储存与丢弃。LSTM解决了RNN模型梯度弥散的问题,可以更好地对具有时空关联的序列数据进行刻画。
假设输入序列X为(x1,x2…,xt),隐藏层状态H为(h1,h2…,ht),使用激活函数对遗忘信息进行计算:
| $ {\mathit{\boldsymbol{f}}_t} = \sigma \left( {{\mathit{\boldsymbol{W}}_{xf}}{x_t} + {\mathit{\boldsymbol{W}}_{hf}}{h_{t - 1}} + {\mathit{\boldsymbol{b}}_f}} \right), $ | (1) |
式中:ft为t时刻遗忘门的输出;σ为激活函数;Wxf为输入层到遗忘门的权重向量;xt为当前t时刻网络的输入;Whf为隐藏层到遗忘门的权重向量;ht-1为上一个时刻隐藏层的状态;bf为遗忘门的偏置。
通过输入门对信息进行更新:
| $ {\mathit{\boldsymbol{i}}_t} = \sigma \left( {{\mathit{\boldsymbol{W}}_{xi}}{x_t} + {\mathit{\boldsymbol{W}}_{hi}}{h_{t - 1}} + {\mathit{\boldsymbol{b}}_i}} \right), $ | (2) |
| $ {\mathit{\boldsymbol{C}}_{t1}} = {\rm{tanh}}\left( {{\mathit{\boldsymbol{W}}_{xc}}{x_t} + {\mathit{\boldsymbol{W}}_{hc}}{h_{t - 1}} + {\mathit{\boldsymbol{b}}_c}} \right), $ | (3) |
式中:it为t时刻输入门的输出;Wxi为输入层到输入门的权重向量;bi为输入门的偏置;Ct1为当前时刻细胞单元的状态;tanh为激活函数;Wxc为输入层到输出门的权重向量;bc为细胞单元的偏置。
将遗忘门与输出门的计算结果相结合,得到当前时刻细胞单元的输出
| $ {\mathit{\boldsymbol{C}}_t} = {\mathit{\boldsymbol{f}}_t} * {\mathit{\boldsymbol{C}}_{t - 1}} + {\mathit{\boldsymbol{i}}_t} * {\mathit{\boldsymbol{C}}_{t1}}, $ | (4) |
式中:*为向量元素相乘;Ct-1为上一时刻细胞单元的状态。
在新的细胞单元上计算输出结果:
| $ {\mathit{\boldsymbol{o}}_t} = \sigma \left( {{\mathit{\boldsymbol{W}}_{xo}}{x_t} + {\mathit{\boldsymbol{W}}_{ho}}{h_{t - 1}} + {\mathit{\boldsymbol{b}}_o}} \right), $ | (5) |
| $ {\mathit{\boldsymbol{h}}_t} = {\mathit{\boldsymbol{o}}_t}\; * {\rm{tanh}}\left( {{c_t}} \right), $ | (6) |
式中:ot为t时刻输出门的输出;Wxo为输入层到输出门的权重向量;Who为输入们与细胞单元状态的权重向量;bo为输出门的偏置;ht为t时刻交通流序列的预测值。
LSTM的内部结构如图 1所示。
|
图 1 LSTM的内部结构 Fig. 1 Internal structure of LSTM |
ED结构是深度学习中的一种模型框架。使用单一的LSTM模型对较长的序列进行预测时,每一步的预测误差将会随着预测步长的增加而增加,从而使预测得到的序列与原始序列存在较大的偏差。ED结构通过编码器将长序列编码为一段向量表示,使用解码器对该向量进行解读并预测,可以有效解决这一问题。
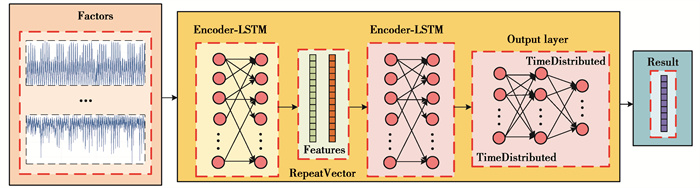
2 基于ED LSTM模型的预测方法文中ED LSTM模型的结构如图 2所示。
|
图 2 文中ED LSTM模型的结构 Fig. 2 tructure of the proposed ED LSTM model |
首先,定义一个单层LSTM作为解码器对输入序列进行读取,并使用RepeatVector层将LSTM输出序列中的每个时间步长的值重复一次,作为解码过程的输入。然后,定义一个单层LSTM模型作为解码层。最后,通过2个TimeDistributed包装器对每个时间步长进行解释并输出。具体预测步骤如表 1所示。
| 表 1 ED LSTM模型的预测步骤 Table 1 The prediction steps of the ED LSTM model |
表 1中,第1~11步用于获得ED LSTM模型的最佳参数设置,第12步用于验证ED结构的有效性,第13步用于验证LSTM学习时间序列显著特征的有效性,第14步用于验证ED LSTM模型具备有效提取多变量交通流序列中深层特征的能力。
其中损失函数MSE为
| $ {L_{{\rm{MSE}}}} = \frac{1}{n}{\sum\limits_{i = 1}^n {\left( {{y_i} - {{\widehat y}_i}} \right)} ^2}, $ | (7) |
式中:n为样本个数;yi为样本实际观测值;ŷi为样本预测值。
3 实例验证为对模型效果进行测试,基于2个城市交通数据集,将传统统计模型:自回归滑动平均(auto-regressive and moving average, ARMA);浅层机器学习模型:SVR、极端梯度提升(extreme gradient boosting, XGBOOST);基准深度学习模型:循环神经网络(recurrent neural network, RNN)、卷积神经网络(convolutional neural networks, CNN)、LSTM模型作为对照组进行实验验证。
3.1 数据来源第1个数据集来源于美国加利福尼亚州第4区高速公路某个路段的数据,简称PEMS-04,数据集的时间跨度为2018年1月1日~2018年6月13日,取工作日从早高峰开始到晚高峰结束之间的时段,即7:00~19:00,每组数据的采样时间间隔为5 min,样本总量为16 992个,特征为交通流量、速度。第2个数据集为中国陕西省西安市市内某路段的交通数据,简称Xi-an,数据集的时间跨度为2020年11月1日~12月25日,取工作日从早高峰开始到晚高峰结束之间的时段,即7:00~20:00,每组数据的采样时间间隔为5 min,样本总量为8 640,特征为流量。
3.2 数据预处理数据规约。文中使用Min-Max函数对数据做归一化操作,将流量及速度数据规约至[0, 1]区间,以此提高模型的收敛速度和预测能力。
训练集与测试集的划分。2个数据集均以8∶2的比例划分训练集与测试集。
3.3 模型参数设置及评价指标选取 3.3.1 模型的参数设置文中ED LSTM模型及基准深度学习模型的建立均基于TensorFlow的深度学习框架。基准深度学习模型的隐藏层个数均为1,隐藏层神经元个数均为64。深度学习模型均使用Relu函数作为激活函数,MSE作为损失函数,Adam作为优化器,batch_size为1,其余均为默认参数。对于模型学习过程的配置,使用Compile方法完成,设置最大训练迭代次数为100,当监测到损失函数停止改进或者迭代次数达到100时结束训练。
统计模型ARMA的建立基于Statsmodels库,模型的参数为默认值。
机器学习模型SVR的建立基于Sklearn库,模型的参数为默认值。XGBOOST模型的建立基于Xgboost库,模型的参数为默认值。
3.3.2 评价指标选取为了客观评价模型的性能,同时选取均方根误差(root mean squard error,RMSE)及平均绝对误差(mean absolute error,MAE)作为模型的评价指标。模型的RMSE、MAE越小,预测效果越好。
3.4 实验设计与评价 3.4.1 单变量实验设计基于PEMS-04、Xi-an 2个数据集,以t-8到t的9个时间步长作为内核尺度读取交通流量数据作为输入序列,对从t+1到t+12的12个步长的交通流量数据进行预测。将ED LSTM模型与对照组模型在12个时间步长内的平均预测RMSE和MAE进行对比,结果如表 2所示。
| 表 2 ED LSTM模型与对照组模型在12个时间步长内的平均预测RMSE和MAE对比 Table 2 The mean predicted RMSE and MAE over 12 time steps by the ED LSTM model and the control models |
由表 2得,ED LSTM模型在从t+1到t+12的12个步长内的平均预测RMSE和平均MAE值均小于对照组模型。在PEMS-04数据集上,与对照组模型相比,ED LSTM模型的RMSE降低了约0.210~5.422,MAE降低约0.061~0.191;在Xi-an数据集上,与对照组模型相比,ED LSTM模型的RMSE降低了约0.210~2.430,MAE降低约0.053~0.239,证明了ED LSTM模型在多步预测方面具有较为优秀的性能。除此之外,实验结果还表明,相较于传统统计模型及浅层机器学习模型,RNN、CNN及LSTM等深度学习模型具备更好的预测效果,能够更有效地学习到时间序列数据的特征。相比其他单一模型,LSTM进一步降低了预测误差,说明LSTM能够更好地对交通流序列进行解释。
继续对单变量ED LSTM模型对于特定时间步长的预测能力进行分析,基于PEMS-04数据集、Xi-an 2个数据集,设定以t-8到t的9个时间步长作为内核尺度读取交通流量数据作为输入序列,对t+1、t+3、t+6、t+12时刻的交通流量数据进行预测。将ED LSTM模型与对照组模型在多个特定时间步长下的平均预测RMSE和MAE进行对比,结果如表 3和表 4所示。
| 表 3 ED LSTM模型与对照组模型在多个特定时间步长下的平均预测RMSE和MAE对比(PEMS-04数据集) Table 3 The mean predicted RMSE and MAE for multiple specific time steps by the ED LSTM model and the control models (PEMS-04 dataset) |
| 表 4 ED LSTM模型与对照组模型在多个特定时间步长下的平均预测RMSE和MAE对比(Xi-an数据集) Table 4 The mean predicted RMSE and MAE for multiple specific time steps by the ED LSTM model and the control models (Xi-an dataset) |
由表 3和表 4得,时间步长对预测的结果影响较大。模型在以较长时间步长进行预测时,会将上一个预测结果考虑在内,因此随着预测步长的增加,模型会产生较大的误差。ED LSTM模型在不同的时间步长下相较于对照组都具有较小的RMSE及MAE,因此单变量输入的ED LSTM模型在不同的预测时间步长下表现均较为优秀。除此之外,相较于LSTM的单一模型,ED LSTM模型性能的下降趋势较为缓慢,说明ED结构能够减缓随着预测步长的增加模型误差迅速积累的趋势,实现更为准确的多步交通流预测。
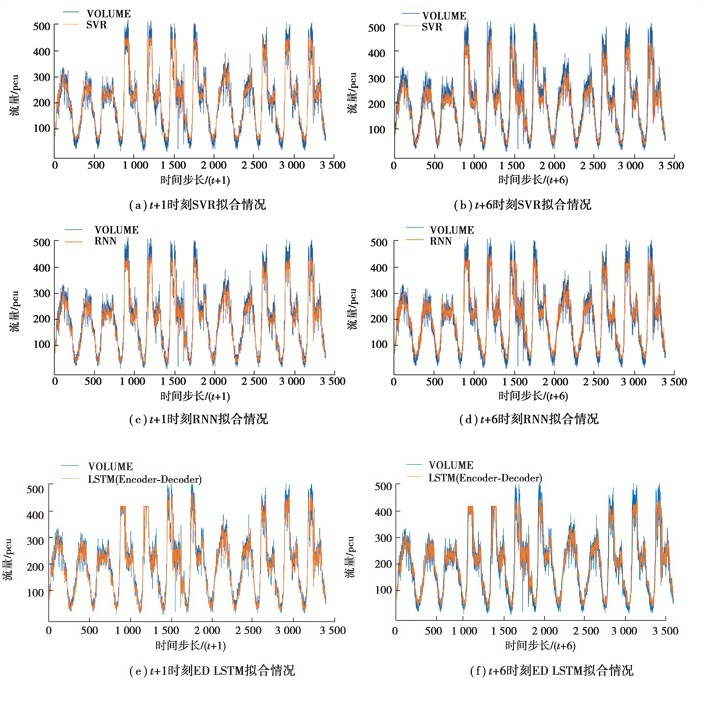
单变量ED LSTM模型与对照组模型在多个特定时间步长下在测试集上的拟合效果如图 3所示。
|
图 3 单变量ED LSTM模型与对照组模型在多个特定时间步长下在测试集上的拟合效果 Fig. 3 The fitting effect of univariate ED LSTM model and control models on test set at multiple specific time |
由图 3得,不论在交通流量序列的波峰还是波谷,相较于对照组模型,ED LSTM模型的预测曲线都能够更好地与交通流量的真实值曲线相拟合。
3.4.2 单变量与多变量对比实验设计为分析单变量与多变量建模对交通流预测的影响,基于PEMS-04数据集,分别以t-8到t的9个时间步长作为内核尺度读取交通流量数据作为输入序列,对从t+1到t+12的12个步长的交通流量数据进行预测。将多变量输入的ED LSTM模型与单变量输入的ED LSTM模型在12个时间步长内的平均预测RMSE和MAE进行对比,结果如表 5所示。
| 表 5 多变量输入的ED LSTM模型与单变量输入的ED LSTM模型在12个时间步长内的平均预测RMSE和MAE对比 Table 5 The average predicted RMSE and MAE over 12 time steps by the ED LSTM model with multivariate inputs and the ED LSTM model with univariate inputs |
由表 5得,相较于单变量输入,ED LSTM模型在多变量时间序列输入的条件下RMSE降低了0.840,MAE降低了0.136,说明ED LSTM模型能够很好地对多变量交通流序列中的非线性特征进行学习。
继续对多变量ED LSTM模型的多步长预测能力进行分析,基于PEMS-04数据集,设定以t-8到t的9个时间步长作为内核尺度读取交通流量数据作为输入序列,对t+1、t+3、t+6、t+12时刻的交通流量数据进行预测。将多变量输入的ED LSTM模型与单变量输入的ED LSTM模型在多个特定时间步长下的平均预测RMSE和MAE进行对比,结果如表 6所示。
| 表 6 多变量输入的ED LSTM模型与单变量输入的ED LSTM模型在多个特定时间步长下的平均预测RMSE和MAE对比 Table 6 The average predicted RMSE and MAE of the ED LSTM model with multivariate inputs and the ED LSTM model with univariate inputs at multiple specific time steps |
由表 6得,在不同的时间步长下,相较于单变量输入,多变量输入的ED LSTM模型的RMSE及MAE均较小。证明了相较于单变量输入,ED LSTM模型在不同的时间步长下均能够较好地学习多变量时间序列中复杂的非线性关系。
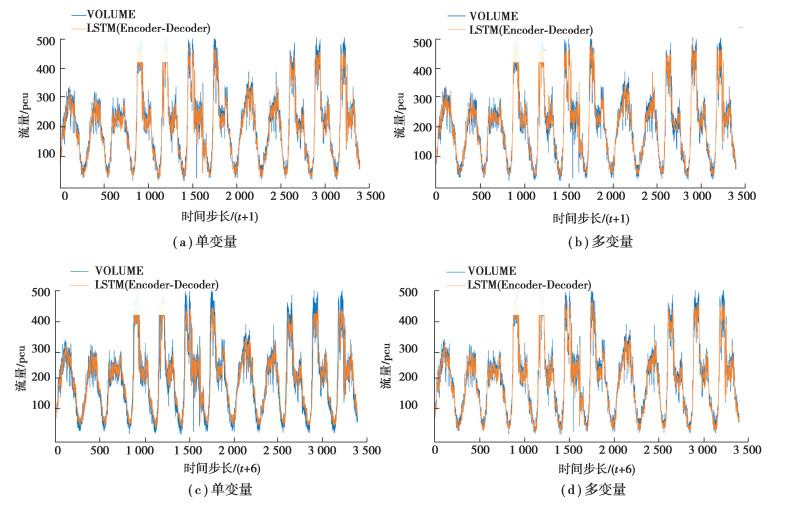
多变量ED LSTM模型与对照组模型在多个特定时间步长下在测试集上的拟合效果如图 4所示。
|
图 4 多变量ED LSTM模型与对照组模型在多个特定时间步长下在测试集上的拟合效果图 Fig. 4 The fitting renderings of the multivariable ED LSTM model and the control models on the test set at multiple specific time steps |
由图 4得,不论在交通流量序列的波峰还是波谷,相较于单变量输入的ED LSTM模型,多变量输入的ED LSTM模型的预测曲线与原预测序列的匹配程度均更好。
4 结束语采用Encoder-Decoder学习框架,构建了一个有效的ED LSTM模型用于交通流预测任务。使用ARMA、SVR、XGBOOST、RNN、CNN、LSTM模型作为对照组,通过控制交通流变量的输入个数及预测的时间步长设计了多个实验对模型的效果进行验证。
1) 采用Encoder-Decoder学习框架,解决了因时间序列较长及多步预测所引起的模型预测误差迅速累积的问题。
2) 采用LSTM作为编码器对多因素交通流序列的非线性特征进行拟合,充分挖掘了交通流序列中多个变量之间的非线性关系。
3) 通过在2个数据集上进行验证,证明了ED LSTM模型可以用于单因素或多因素的交通流序列的多步预测问题。
但交通流仍受天气、能见度等因素的影响,下一步研究可以考虑获取其他因素的相关数据,挖掘更多影响因素之间的非线性关系。
| [1] |
Williams B M, Hoel L A. Modeling and forecasting vehicular traffic flow as a seasonal ARIMA process: theoretical basis and empirical results[J]. Journal of Transportation Engineering, 2003, 129(6): 664-672. DOI:10.1061/(ASCE)0733-947X(2003)129:6(664) |
| [2] |
Smith B L, Williams B M, Oswald R K. Comparison of parametric and nonparametric models for traffic flow forecasting[J]. Transportation Research Part C: Emerging Technologies, 2002, 10(4): 303-321. DOI:10.1016/S0968-090X(02)00009-8 |
| [3] |
Hu W, Yan L, Liu K, et al. A short-term traffic flow forecasting method based on the hybrid PSO-SVR[J]. Neural Processing Letters, 2016, 43(1): 155-172. DOI:10.1007/s11063-015-9409-6 |
| [4] |
张文胜, 郝孜奇, 朱冀军, 等. 基于改进灰狼算法优化BP神经网络的短时交通流预测模型[J]. 交通运输系统工程与信息, 2020, 20(2): 196-203. Zhang W S, Hao Z Q, Zhu J J, et al. BP neural network model for short-time traffic flow forecasting based on transformed grey wolf optimizer algorithm[J]. Journal of Transportation Systems Engineering and Information Technology, 2020, 20(2): 196-203. (in Chinese) |
| [5] |
孔繁辉, 李健. 深度信念网络优化BP神经网络的交通流预测模型[J]. 管理评论, 2020, 32(3): 300-306. Kong F H, Li J. Traffic flow prediction model based on deep belief network optimized BP neural network[J]. Management Review, 2020, 32(3): 300-306. (in Chinese) |
| [6] |
吕明琪, 洪照雄, 陈铁明. 一种融合时空关联与社会事件的交通流预测方法[J]. 计算机科学, 2021, 48(2): 264-270. Lyu M Q, Hong Z X, Chen T M. Traffic flow forecasting method combining spatio-temporal correlations and social events[J]. Computer Science, 2021, 48(2): 264-270. (in Chinese) |
| [7] |
Ma X, Tao Z, Wang Y, et al. Long short-term memory neural network for traffic speed prediction using remote microwave sensor data[J]. Transportation Research Part C: Emerging Technologies, 2015, 54: 187-197. DOI:10.1016/j.trc.2015.03.014 |
| [8] |
Fu R, Zhang Z, Li L. Using LSTM and GRU neural network methods for traffic flow prediction[C]//2016 31st Youth Academic Annual Conference of Chinese Association of Automation (YAC). IEEE, 2016: 324-328.
|
| [9] |
郑乐军, 文成林. 基于集成学习的交通流短时特性分析与神经网络预测方法[J]. 科学技术与工程, 2021, 21(4): 1615-1623. Zheng L J, Wen C L. Analysis of short-term characteristics of traffic flow based on ensemble learning and neural network prediction method[J]. Science Technology and Engineering, 2021, 21(4): 1615-1623. (in Chinese) DOI:10.3969/j.issn.1671-1815.2021.04.053 |
| [10] |
叶景, 李丽娟, 唐臻旭. 基于CNN-XGBoost的短时交通流预测[J]. 计算机工程与设计, 2020, 41(4): 1080-1086. Ye J, Li L J, Tang Z X. Short-term traffic flow forecasting based on CNN-XGBoost[J]. Computer Engineering and Design, 2020, 41(4): 1080-1086. (in Chinese) |
| [11] |
李浩, 张杉, 曹斌, 等. 基于城市道路卡口数据的交通流量预测[J]. 重庆大学学报, 2020, 43(11): 29-40. Li H, Zhang S, Cao B, et al. Prediction traffic flow based on teaffic data of urban road check points[J]. Journal of Chongqing University, 2020, 43(11): 29-40. (in Chinese) DOI:10.11835/j.issn.1000-582X.2020.11.004 |
| [12] |
Li Y, Yu R, Shahabi C, et al. Diffusion convolutional recurrent neural network: data-driven traffic forecasting[J]. arXiv preprint arXiv: 1707.01926, 2017.
|
| [13] |
陈晓利, 韩锋斌. 基于多智能体的城市环道交通信号控制算法[J]. 重庆大学学报, 2021, 44(1): 37-45, 118. Chen X L, Han F B. An urban ring road traffic signal control algorithm based on multi-agents[J]. Journal of Chongqing University, 2021, 44(1): 37-45, 118. (in Chinese) |
| [14] |
丁洁, 刘晋峰, 杨祖莨, 等. 基于深度学习的交通拥堵检测[J]. 重庆大学学报, 2021, 44(4): 107-116. Ding J, Liu J F, Yang Z L, et al. Traffic congestion detection based on deep learning[J]. Journal of Chongqing University, 2021, 44(4): 107-116. (in Chinese) |
| [15] |
刘琳, 李春媛, 陈彦虎, 等. 基于路由节点的最优油耗路径规划模型[J]. 重庆大学学报, 2018, 41(7): 73-81. Liu L, Li C Y, Chen Y H, et al. Research on path planning model of optimal fuel consumption based on routing nodes[J]. Journal of Chongqing University, 2018, 41(7): 73-81. (in Chinese) |
| [16] |
Dongfang M, Song X B, Zhu J C, et al. Input data selection for daily traffic flow forecasting through contextual mining and intra-day pattern recognition[J]. Expert Systems with Applications, 2021, 176. |
 2021, Vol. 44
2021, Vol. 44


