电动汽车电驱动一体化设计已成为当前的研究热点[1],但由于系统时刻受到来自外部和内部激励的影响,可能导致机电传动系统性能的恶化。扭转减振装置具有缓冲、减振的作用,通过改变系统固有特性可以改善复杂工况下传动系统性能。行星齿轮具有单级速比大、结构紧凑、承载能力强的特点,在汽车、风机、采煤机及飞行器等众多领域广泛应用[2-3]。电机行星齿轮传动作为主要的动力传输部分,时刻承受来自电机端和负载端激励力及齿轮系统内部的多种激励[4],这是引起机电传动系统载荷波动和扭转振动的主要原因,对传动系统的平顺性和稳定性有着重要的影响。因此改善电机行星齿轮传动系统的动态特性尤为重要。
对于发动机驱动的传动系统的研究已经较为成熟,发动机转矩波动剧烈对系统影响较大,一般采用扭转减振装置或双质量飞轮,通过调整系统动力学参数来改善系统动态特性[5-7]。文献[6]分析了双质量飞轮参数对传动系统扭振控制的影响,并在一定约束条件下进行双质量飞轮多级扭转刚度的匹配设计。对于电机驱动的传动系统,文献[8-9]建立了不同的电机模型,并分析了不同情况下电机、齿轮系统耦合的动态特性,包括状态监测、故障诊断等。文献[10-11]通过对电机的控制实现了传动系统的主动降振,减小系统冲击载荷作用下的动载荷。
对于行星齿轮动力学已有较多的研究,文献[12-14]分别建立单级行星齿轮动力学模型,揭示了行星齿轮的振动模式,分析了系统固有特性对系统刚度、惯量及转速的敏感度。文献[15]分析了非平稳运行下行星齿轮系统的振动特性,考虑了负载波动对齿轮啮合频率的影响。文献[16]建立了行星平行轴风电齿轮传动系统模型,分析了内部激励因素对齿轮箱振动的影响。文献[17]分析了在复杂激励下,轮齿修形对行星齿轮箱振动噪声的影响。文献[18]分析了风电行星齿轮系统在同时受外部激励和内部激励下传动系统的动态特性。文献[19]提出了一种用于变速过程的人字形行星齿轮的平移扭转模型,选择平移位移和角位移作为广义坐标。
上述研究中大部分行星齿轮模型仅可用于系统固有特性分析或恒速下的振动分析,以振动位移或行星架动坐标系下的角位移作为广义坐标。为了改善内、外部激励下电机行星齿轮传动系统的振动特性,笔者提出了扭转减振装置与行星齿轮耦合的自减振行星传动系统,将这种新型传动形式称为TVD-PG(torsional vibration damper and planetary gear)传动系统,采用扭转减振装置取代传统行星齿轮某一构件与箱体固连的方式。以扭转减振装置耦合内齿圈为例,建立了适用于变速情况下的电机-TVD-PG系统动力学模型,考虑行星齿轮系统内部时变刚度激励的影响,并修改了行星齿轮时变啮合刚度模型,将其表示为关于太阳轮实际角位移的函数。在MATLAB/Simulink平台进行仿真,获得电机部分的电磁转矩、转速,齿轮系统的啮合力、输出端转速等响应曲线,并与传统电机行星齿轮(PG)传动系统进行对比,凸显TVD-PG传动系统在启动升速到稳定过程中的优势。
1 电机-TVD-PG系统动力学模型TVD-PG传动系统采用扭转减振装置取代了传统的行星齿轮中某一构件与箱体固连的方式,另外两个中心构件分别作为输入和输出端,可组成3种不同的结构形式。以扭转减振装置耦合内齿圈为例,扭转减振装置主动端与内齿圈相连,从动端与箱体刚性固连。采用集中参数法建立了可适用于变速工况下的TVD-PG传动系统动力学模型,其中各齿轮构件简化为集中质量或惯量,传动轴简化为集中刚度和阻尼连接,忽略齿轮系统的误差激励、轮齿间摩擦力、齿侧间隙,且单齿啮合刚度恒定。
由于机电传动系统经常受到来自外界和内部不断变化的激励作用,因此系统瞬态响应必须被考虑。与上述提到的行星齿轮动力学模型所不同,选用各构件角位移为系统广义坐标,太阳轮和内齿圈的角位移在静坐标系中获得,可以与电机直接相连。所建立的适用于变速情况下的TVD-PG系统动力学模型如图 1所示。其中建立了3种坐标系:OXY为固定坐标系;Oxy为与行星架固连并随行星架旋转的转动坐标系,x轴通过第一个行星轮中心;Onxnyn(n=1, 2, …, N,N代表行星轮个数)为与行星架固联并随行星架旋转的转动坐标系,On为行星轮中心,两坐标轴分别与Oxy坐标系的两坐标轴平行。下标c,r,s,n分别代表行星架、内齿圈、太阳轮和第n个行星轮。θi(i=c, s, r)表示构件在OXY坐标系下的角位移,θn表示行星轮在Onxnyn坐标系下的角位移;Jj(j=c, s, r, n)为构件转动惯量;rk(k=s, r, n)为构件基圆半径,rc为行星架有效半径;ksn,csn,krn,crn分别为太阳轮与第n个行星轮、第n个行星轮与内齿圈间的啮合刚度和啮合阻尼;kr,cr分别为扭转减振装置扭转刚度和阻尼;Ts,Tc分别为作用在太阳轮和行星架端的转矩。利用牛顿定律获得TVD-PG传动系统数学模型,如式(1)所示。
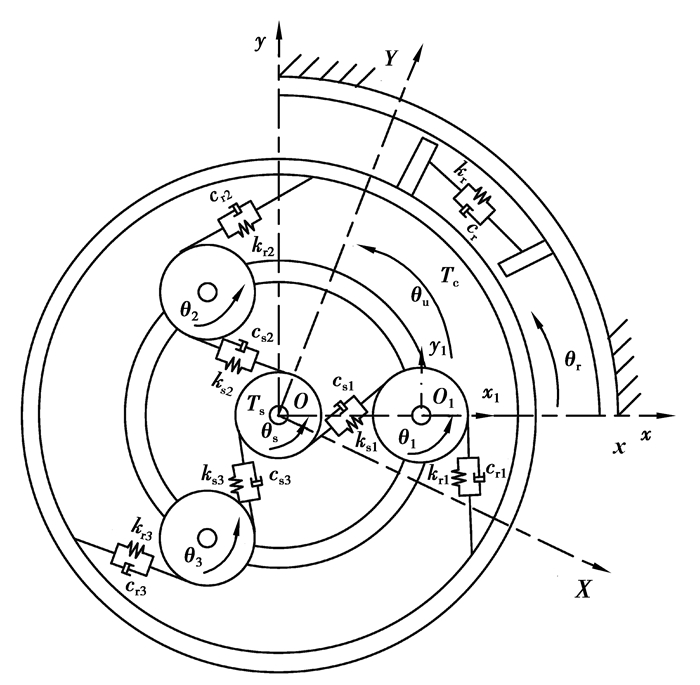
|
图 1 TVD-PG系统动力学模型 Fig. 1 Dynamic model of the TVD-PG |
| $ \left\{ \begin{array}{l} \begin{array}{*{20}{l}} {{J_{\rm{c}}}{{\ddot \theta }_{\rm{c}}} = \sum\limits_{n = 1}^3 {\left( {{k_{{\rm{s}}n}}{\delta _{{\rm{s}}n}} + {c_{{\rm{s}}n}}{{\dot \delta }_{{\rm{s}}n}}} \right)} {r_{\rm{c}}}\cos {\alpha _{\rm{s}}} + \sum\limits_{n = 1}^3 {\left( {{k_{{\rm{r}}n}}{\delta _{{\rm{r}}n}} + {c_{{\rm{r}}n}}{{\dot \delta }_{{\rm{r}}n}}} \right)} {r_{\rm{c}}}\cos {\alpha _{\rm{r}}} - {T_{\rm{c}}},}\\ {{J_{\rm{r}}}{{\ddot \theta }_{\rm{r}}} - \sum\limits_{n = 1}^3 {\left( {{k_{{\rm{r}}n}}{\delta _{{\rm{r}}n}} + {c_{{\rm{r}}n}}{{\dot \delta }_{{\rm{r}}n}}} \right)} {r_{\rm{r}}} - {k_{\rm{r}}}{\theta _{\rm{r}}} - {c_{\rm{r}}}{{\dot \theta }_{\rm{c}}} = 0,}\\ {{J_{\rm{s}}}{{\ddot \theta }_{\rm{s}}} = {T_{\rm{s}}} - \sum\limits_{n = 1}^3 {\left( {{k_{{\rm{s}}n}}{\delta _{{\rm{s}}n}} + {c_{{\rm{s}}n}}{{\dot \delta }_{{\rm{s}}n}}} \right)} {r_{\rm{c}}},} \end{array}\\ \begin{array}{*{20}{l}} {{J_1}{{\ddot \theta }_1} = \left( {{k_{{\rm{r1}}}}{\delta _{{\rm{r1}}}} + {c_{{\rm{r1}}}}{{\dot \delta }_{{\rm{r1}}}} - {k_{{\rm{s}}1}}{\delta _{{\rm{s}}1}} - {c_{{\rm{s}}1}}{{\dot \delta }_{{\rm{s}}1}}} \right){r_1},}\\ {{J_2}{{\ddot \theta }_2} = \left( {{k_{{\rm{r}}2}}{\delta _{{\rm{r}}2}} + {c_{{\rm{r}}2}}{{\dot \delta }_{{\rm{r}}2}} - {k_{{\rm{s}}2}}{\delta _{{\rm{s}}2}} - {c_{{\rm{s}}2}}{{\dot \delta }_{{\rm{s}}2}}} \right){r_2},}\\ {{J_3}{{\ddot \theta }_3} = \left( {{k_{{\rm{r}}3}}{\delta _{{\rm{r}}3}} + {c_{{\rm{r}}3}}{{\dot \delta }_{{\rm{r}}3}} - {k_{{\rm{s}}3}}{\delta _{{\rm{s}}3}} - {c_{{\rm{s}}3}}{{\dot \delta }_{{\rm{s}}3}}} \right){r_3}}。\end{array} \end{array} \right. $ | (1) |
式中:δsn为太阳轮相对于第n个行星轮沿外啮合线方向的相对变形量;δsn为内齿圈相对于第n个行星轮沿内啮合线方向的相对变形量,表示为
| $ \left\{ {\begin{array}{*{20}{l}} {{\delta _{{\rm{s}}n}} = \left( {{\theta _s} - {\theta _{\rm{c}}}} \right){r_{\rm{s}}} + {r_n}{\theta _n},}\\ {{\delta _{{\rm{r}}n}} = \left( {{\theta _{\rm{r}}} - {\theta _{\rm{c}}}} \right){r_{\rm{r}}} - {r_n}{\theta _n}}。\end{array}} \right. $ | (2) |
建立的电机-TVD-PG传动系统模型中选用鼠笼式异步电机,将转子的角位移和角速度作为电机与TVD-PG传动系统间耦合的公共变量,实时计算的电机输出轴上的转矩作为电机的负载,进而形成电机-TVD-PG耦合仿真模型,如图 2所示。得到电机转子和负载端动力学方程如式(3)所示,作用在太阳轮和行星架上的转矩由式(4)给出。
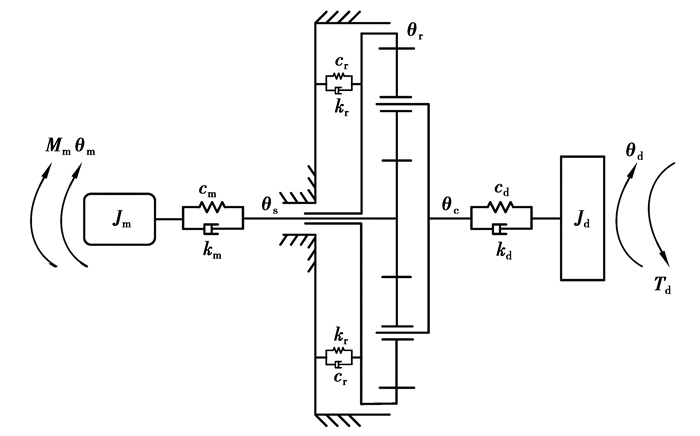
|
图 2 电机-TVD-PG系统模型 Fig. 2 Model of the motor-TVD-PG system |
| $ \left\{ {\begin{array}{*{20}{c}} {{J_{\rm{m}}}{{\ddot \theta }_{\rm{m}}} = {M_{\rm{m}}} - {k_{\rm{m}}}\left( {{\theta _{\rm{m}}} - {\theta _{\rm{s}}}} \right) - {c_{\rm{m}}}\left( {{{\dot \theta }_{\rm{m}}} - {{\dot \theta }_{\rm{s}}}} \right),}\\ {{J_{\rm{d}}}{{\ddot \theta }_{\rm{d}}} = {k_{\rm{d}}}\left( {{\theta _{\rm{c}}} - {\theta _{\rm{d}}}} \right) + {c_{\rm{d}}}\left( {{{\dot \theta }_{\rm{c}}} - {{\dot \theta }_{\rm{d}}}} \right) - {T_{\rm{d}}}}。\end{array}} \right. $ | (3) |
| $ {\left\{ {\begin{array}{*{20}{l}} {{T_{\rm{s}}} = {k_{\rm{m}}}\left( {{\theta _{\rm{m}}} - {\theta _{\rm{s}}}} \right) + {c_{\rm{m}}}\left( {{{\dot \theta }_{\rm{m}}} - {{\dot \theta }_{\rm{s}}}} \right),}\\ {{T_{\rm{c}}} = {k_{\rm{d}}}\left( {{\theta _{\rm{c}}} - {\theta _{\rm{d}}}} \right) + {c_{\rm{d}}}\left( {{{\dot \theta }_{\rm{c}}} - {{\dot \theta }_{\rm{d}}}} \right)}。\end{array}} \right.} $ | (4) |
电机-TVD-PG传动系统动力学方程可表示为矩阵方程的形式,即
| $ \mathit{\boldsymbol{M\ddot q}} + \left( {{\mathit{\boldsymbol{C}}_{\rm{m}}} + {\mathit{\boldsymbol{C}}_{\rm{t}}} + {\mathit{\boldsymbol{C}}_{\rm{b}}}} \right)\mathit{\boldsymbol{\dot q}} + \left( {{\mathit{\boldsymbol{K}}_{\rm{m}}} + {\mathit{\boldsymbol{K}}_{\rm{t}}} + {\mathit{\boldsymbol{K}}_{\rm{b}}}} \right)\mathit{\boldsymbol{q}} = \mathit{\boldsymbol{T}}, $ | (5) |
式中:q为广义坐标阵列
| $ {\mathit{\boldsymbol{q}} = {{\left[ {\begin{array}{*{20}{l}} {{\theta _{\rm{m}}}}&{{\theta _{\rm{c}}}}&{{\theta _{\rm{r}}}}&{{\theta _{\rm{s}}}}&{{\theta _1}}&{{\theta _2}}&{{\theta _3}}&{{\theta _d}} \end{array}} \right]}^{\rm{T}}};} $ | (6) |
M为质量矩阵
| $ {\mathit{\boldsymbol{M}} = {\mathop{\rm diag}\nolimits} \left[ {\begin{array}{*{20}{l}} {{J_{\rm{m}}}}&{{J_{\rm{c}}} + N \cdot {m_{\rm{p}}} \cdot r_{\rm{c}}^2}&{{J_{\rm{r}}}}&{{J_{\rm{s}}}}&{{J_1}}&{{J_2}}&{{J_3}}&{{J_{\rm{d}}}} \end{array}} \right];} $ | (7) |
T为外力矩阵
| $ {\mathit{\boldsymbol{T}} = {{\left[ {\begin{array}{*{20}{l}} {{T_{\rm{m}}}}&0&0&0&0&0&0&{{T_{\rm{d}}}} \end{array}} \right]}^{\rm{T}}};} $ | (8) |
Km,Kt,Kb,Cm,Ct,Cb分别为啮合刚度矩阵、扭转刚度矩阵、支撑刚度矩阵、啮合阻尼矩阵、支承阻尼矩阵和支撑阻尼矩阵。其中(Km+Kt+Kb)整体可表示为系统刚度矩阵K,其形式如式(9)所示,系统阻尼矩阵(Cm+Ct+Cb)与刚度矩阵形式类似,这里不再列出。仿真所用到的TVD-PG传动系统主要参数见表 1。
| $ \mathit{\boldsymbol{K}} = \left[ {\begin{array}{*{20}{c}} {{k_{\rm{m}}}}&0&0&{ - {k_{\rm{m}}}}&0&0&0&0\\ 0&\begin{array}{l} \sum\limits_{n = 1}^3 {{k_{{\rm{s}}n}}} r_{\rm{c}}^2{\cos ^2}{\alpha _{\rm{s}}} + \\ \sum\limits_{n = 1}^3 {{k_{{\rm{r}}n}}} r_{\rm{c}}^2{\cos ^2}{\alpha _{\rm{r}}} + {K_{\rm{d}}} \end{array}&{ - \sum\limits_{n = 1}^3 {{k_{{\rm{r}}n}}} {r_{\rm{r}}}{r_{\rm{c}}}\cos {\alpha _{\rm{r}}}}&{ - \sum\limits_{n = 1}^3 {{k_{{\rm{s}}n}}} {r_{\rm{s}}}{r_{\rm{c}}}\cos {\alpha _{\rm{s}}}}&\begin{array}{l} {k_{{\rm{r1}}}}{r_1}{r_{\rm{c}}}\cos {\alpha _{\rm{r}}} - \\ {k_{{\rm{s1}}}}{r_1}{r_{\rm{c}}}\cos {\alpha _{\rm{s}}} \end{array}&\begin{array}{l} {k_{{\rm{r}}2}}{r_2}{r_{\rm{c}}}\cos {\alpha _{\rm{r}}} - \\ {k_{{\rm{s}}2}}{r_2}{r_{\rm{c}}}\cos {\alpha _{\rm{s}}} \end{array}&\begin{array}{l} {k_{{\rm{r}}3}}{r_3}{r_{\rm{c}}}\cos {\alpha _{\rm{r}}} - \\ {k_{{\rm{s}}3}}{r_3}{r_{\rm{c}}}\cos {\alpha _{\rm{s}}} \end{array}&{ - {k_{\rm{d}}}}\\ 0&{ - \sum\limits_{n = 1}^3 {{k_{{\rm{r}}n}}} {r_{\rm{r}}}{r_{\rm{c}}}\cos {\alpha _{\rm{r}}}}&{\sum\limits_{n = 1}^3 {{k_{{\rm{r}}n}}} r_r^2 + {k_{\rm{r}}}}&0&{ - {k_{{\rm{r1}}}}{r_1}{r_{\rm{r}}}}&{ - {k_{{\rm{r}}2}}{r_2}{r_{\rm{r}}}}&{ - {k_{{\rm{r}}3}}{r_3}{r_{\rm{r}}}}&0\\ { - {k_{\rm{m}}}}&{ - \sum\limits_{n = 1}^3 {{k_{{\rm{s}}n}}} {r_{\rm{s}}}{r_{\rm{c}}}\cos {\alpha _{\rm{s}}}}&0&{\sum\limits_{n = 1}^3 {{k_{{\rm{s}}n}}} r_{\rm{s}}^2 + {k_{\rm{m}}}}&{{k_{{\rm{s1}}}}{r_1}{r_{\rm{s}}}}&{{k_{{\rm{s}}2}}{r_2}{r_{\rm{s}}}}&{{k_{{\rm{s}}3}}{r_3}{r_{\rm{s}}}}&0\\ 0&{{k_{{\rm{r1}}}}{r_1}{r_{\rm{c}}}\cos {\alpha _{\rm{r}}} - {k_{{\rm{s1}}}}{r_1}{r_{\rm{c}}}\cos {\alpha _{\rm{s}}}}&{ - {k_{{\rm{r1}}}}{r_1}{r_{\rm{r}}}}&{{k_{{\rm{s1}}}}{r_1}{r_{\rm{s}}}}&{{k_{{\rm{s}}1}}r_1^2 + {k_{{\rm{r1}}}}r_1^2}&0&0&0\\ 0&{{k_{{\rm{r}}2}}{r_2}{r_{\rm{c}}}\cos {\alpha _{\rm{r}}} - {k_{{\rm{s}}2}}{r_2}{r_{\rm{c}}}\cos {\alpha _{\rm{s}}}}&{ - {k_{{\rm{r2}}}}{r_2}{r_{\rm{r}}}}&{{k_{{\rm{s}}2}}{r_2}{r_{\rm{s}}}}&0&{{k_{{\rm{s}}2}}r_2^2 + {k_{{\rm{r}}2}}r_2^2}&0&0\\ 0&{{k_{{\rm{r}}3}}{r_3}{r_{\rm{c}}}\cos {\alpha _{\rm{r}}} - {k_{{\rm{s}}3}}{r_3}{r_{\rm{c}}}\cos {\alpha _{\rm{s}}}}&{ - {k_{{\rm{r3}}}}{r_3}{r_{\rm{r}}}}&{{k_{{\rm{s}}3}}{r_3}{r_{\rm{s}}}}&0&0&{{k_{{\rm{s}}3}}r_3^2 + {k_{{\rm{r}}3}}r_3^2}&0\\ 0&{ - {k_{\rm{d}}}}&0&0&0&0&0&{{k_{\rm{d}}}} \end{array}} \right]。$ | (9) |
| 表 1 TVD-PG传动系统参数 Table 1 TVD-PG system parameters |
由于TVD-PG传动系统需要适用于变速工况,齿轮系统啮合频率将随转速不断变化,且系统转速作为未知量,需要实时计算,因此系统的内部激励参数将不能再表示为关于时间的函数,参考文献[9, 20]的方法,将行星齿轮时变啮合刚度表示为关于太阳轮实际角位移的函数,并建立了时变啮合刚度函数模型。时变啮合刚度可表示为啮合刚度均值和变动量之和的形式:
| $ \left\{ {\begin{array}{*{20}{l}} {{k_{{\rm{s}}n}}\left( {{\theta _{\rm{s}}}} \right) = {{\bar k}_{{\rm{s}}n}} + \Delta {k_{{\rm{s}}n}}\left( {{\theta _{\rm{s}}}} \right),}\\ {{k_{{\rm{r}}n}}\left( {{\theta _{\rm{s}}}} \right) = {{\bar k}_{{\rm{r}}n}} + \Delta {k_{{\rm{r}}n}}\left( {{\theta _{\rm{s}}}} \right)}。\end{array}} \right. $ | (10) |
式中:ksn,krn为时变啮合刚度均值,如式(11)所示,Δksn(θs),Δkrn(θs)为啮合刚度的变量部分,以傅立叶级数形式表示,如式(12)所示。
| $ {\left\{ {\begin{array}{*{20}{l}} {{{\bar k}_{{\rm{s}}n}} = {k_{{\rm{sn\_min}}}}\left( {2 - {\varepsilon _{{\rm{s}}n}}} \right) + {k_{{\rm{sn\_max}}}}\left( {{\varepsilon _{{\rm{s}}n}} - 1} \right),}\\ {{{\bar k}_{{\rm{r}}n}} = {k_{{\rm{rn}}\_\min }}\left( {2 - {\varepsilon _{{\rm{r}}n}}} \right) + {k_{{\rm{rn}}\_\max }}\left( {{\varepsilon _{{\rm{r}}n}} - 1} \right)}。\end{array}} \right.} $ | (11) |
| $ {\left\{ {\begin{array}{*{20}{l}} {\Delta {k_{{\rm{s}}n}}\left( {{\theta _{\rm{s}}}} \right) = \sum\limits_{l = 1}^\infty {\left( {a_{{\rm{s}}n}^l\cos \left( {l{Z_{\rm{s}}}\left( {{\theta _{\rm{s}}} - {\theta _{\rm{c}}}} \right) + b_{{\rm{s}}n}^l\sin \left( {l{Z_{\rm{s}}}\left( {{\theta _{\rm{s}}} - {\theta _{\rm{c}}}} \right),} \right.} \right.} \right.} }\\ {\Delta {k_{{\rm{r}}n}}\left( {{\theta _{\rm{s}}}} \right) = \sum\limits_{l = 1}^\infty {\left( {a_{{\rm{r}}n}^l\cos \left( {l{Z_{\rm{s}}}\left( {{\theta _{\rm{s}}} - {\theta _{\rm{c}}}} \right) + b_{{\rm{r}}n}^l\sin \left( {l{Z_{\rm{s}}}\left( {{\theta _{\rm{s}}} - {\theta _{\rm{c}}}} \right)} \right.} \right.} \right.} }。\end{array}} \right.} $ | (12) |
其中asnl,bsnl,arnl,brnl可表示为式(13)所示形式:
| $ \left\{ \begin{array}{l} \begin{array}{*{20}{l}} {a_{{\rm{s}}n}^l = \frac{1}{{l{\rm{ \mathsf{ π} }}}}\left( {{k_{{\rm{s}}n\_\max }} - {k_{{\rm{s}}n\_\min }}} \right)\left\{ {\sin 2l{\rm{ \mathsf{ π} }}\left( {{\varepsilon _{{\rm{s}}n}} - 1} \right)\cos \left( {l{Z_{\rm{s}}}{\psi _n}} \right) + \left[ {1 - \cos 2l{\rm{ \mathsf{ π} }}\left( {{\varepsilon _{{\rm{s}}n}} - 1} \right)} \right]\sin \left( {l{Z_{\rm{s}}}{\psi _n}} \right)} \right\},}\\ {b_{{\rm{s}}n}^l = \frac{1}{{l{\rm{ \mathsf{ π} }}}}\left( {{k_{{\rm{s}}n\_\max }} - {k_{{\rm{s}}n\_\min }}} \right)\left\{ {\left[ {1 - \cos 2l{\rm{ \mathsf{ π} }}\left( {{\varepsilon _{{\rm{s}}n}} - 1} \right)} \right]\cos \left( {l{Z_{\rm{s}}}{\psi _n}} \right) - \sin 2l{\rm{ \mathsf{ π} }}\left( {{\varepsilon _{{\rm{s}}n}} - 1} \right)\sin \left( {l{Z_{\rm{s}}}{\psi _n}} \right)} \right\},} \end{array}\\ \begin{array}{*{20}{l}} {a_{{\rm{r}}n}^l = \frac{1}{{l{\rm{ \mathsf{ π} }}}}\left( {{k_{{\rm{r}}n\_\max }} - {k_{{\rm{r}}n\_\min }}} \right)\left\{ {\sin 2l{\rm{ \mathsf{ π} }}\left( {{\varepsilon _{{\rm{r}}n}} - 1} \right)\cos \left[ {l\left( {{Z_{\rm{r}}}{\psi _n} + {\gamma _{{\rm{sr}}}}} \right)} \right] + \left[ {1 - \cos 2l\pi \left( {{\varepsilon _{{\rm{r}}n}} - 1} \right)} \right]\sin \left[ {l\left( {{Z_{\rm{r}}}{\psi _n} + {\gamma _{{\rm{sr}}}}} \right)} \right]} \right\},}\\ {b_{{\rm{r}}n}^l = \frac{1}{{l{\rm{ \mathsf{ π} }}}}\left( {{k_{{\rm{r}}n\_\max }} - {k_{{\rm{r}}n\_\min }}} \right)\left\{ {\left[ {1 - \cos 2l{\rm{ \mathsf{ π} }}\left( {{\varepsilon _{{\rm{r}}n}} - 1} \right)} \right]\cos \left[ {l\left( {{Z_{\rm{r}}}{\psi _n} + {\gamma _{{\rm{sr}}}}} \right)} \right] - \sin 2l\pi \left( {{\varepsilon _{{\rm{r}}n}} - 1} \right)\sin \left[ {l\left( {{Z_{\rm{r}}}{\psi _n} + {\gamma _{{\rm{sr}}}}} \right)} \right]} \right\}{\rm{ }}}。\end{array} \end{array} \right. $ | (13) |
式(11)~(13)中,ksn_max,krn_max,ksn_min,krn_min分别为内、外啮合刚度的最大和最小值;εsn,εrn分别为内、外啮合重合度;l为谐波次数;Zs,Zr分别为太阳轮和内齿圈齿数;θs,θc分别为太阳轮和行星架的实际角位移;ψn为第n个行星轮中心与坐标原点O的连线同坐标系Oxy中x轴的夹角;γsr为内外啮合相位差。
建立了关于太阳轮实际角位移的时变刚度模型,得到系统转速变化时行星齿轮系统中太阳轮和第1个行星轮间的时变啮合刚度ks1如图 3(a)所示,可以看出啮合频率随转速变化而不断改变。为了显示该啮合刚度模型的啮合频率,图 3(b)给出了恒速时啮合刚度的频域信号,其中fm,2fm,3fm,4fm分别表示行星齿轮前4阶啮合频率。
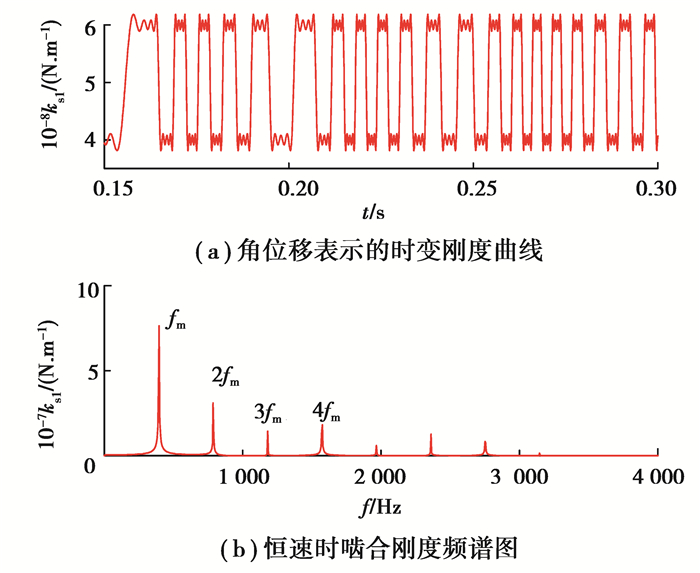
|
图 3 时变啮合刚度 Fig. 3 Time-varying meshing stiffness |
在建立的电机-TVD-PG传动系统机电耦合模型基础上,探究了考虑齿轮系统内部时变啮合刚度激励作用时,在启动和稳定过程中系统的动力学特性,并与传统的行星齿轮传动系统仿真结果进行对比,以表明其所具备的优势。
3.1 启动过程中电机-TVD-PG系统动态响应所建立的机电耦合模型中,为了更好分析电机和齿轮系统的耦合特性,不对电机进行控制。由于系统负载端有较大的转动惯量,且实时计算的电机输出轴上的载荷作为电机负载,所以电机在启动过程中的电磁转矩和转速将产生较大的波动。图 4(a)(b)给出了电机TVD-PG传动系统的电磁转矩Te和电机转速ωm曲线,并与传统的行星齿轮传动进行了对比。可看出由于TVD-PG系统中扭转减振装置的缓冲、减振作用,可以快速减小电磁转矩的波动,电机转速增长相对较为平稳,使电机较快地到达需求转矩和稳定转速。图 4(c)给出了系统输出端转速ωd曲线,可以发现带有TVD-PG的机电系统输出端转速快速稳定增长,且在启动初期转速波动大幅降低。故表明TVD-PG传动系统改善了电机及齿轮系统输出端在启动过程中的动态特性,有助于提高机电传动系统的平顺性和稳定性。
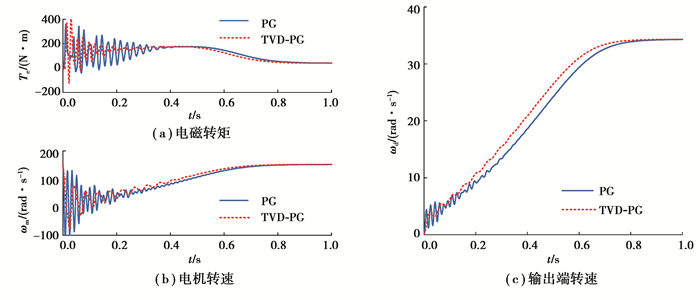
|
图 4 系统响应曲线 Fig. 4 Response curves of systems |
图 5给出了太阳轮和第1个行星轮间外啮合力Fs1和内齿圈与第1个行星轮间内啮合力Fr1在时域和频域响应曲线,用于分析启动过程中行星齿轮部分的动态响应。从图 5(a)(c)中可以清晰看出,TVD-PG系统可以有效降低启动过程中行星齿轮内、外啮合力的波动幅值,并使啮合力快速稳定。内啮合力时域响应图(a)中区域A1和A2啮合力幅值显著增大,对应内啮合力频域图(b)中的区域B1和B2。区域B1处出现峰值的频率为920和1 025 Hz,分别为传统电机行星齿轮系统的第2阶固有频率和电机-TVD-PG系统的第3阶固有频率,与行星齿轮第3阶啮合频率相近;区域B2仅在传统的电机行星齿轮系统中出现,对应峰值频率为2 298 Hz,为传统电机行星齿轮系统的3阶固有频率,与行星齿轮第6阶啮合频率相近。以上区域啮合力幅值显著增大,原因是系统某阶固有频率与行星齿轮某阶啮合频率相接近,系统发生了共振现象,使啮合力显著增大。同理外啮合力时域响应图(c)中区域C1对应频域图(d)中的区域D1,此区域为共振区。对于传统的电机行星齿轮系统外啮合力曲线(c)的第2个共振区域,由于振动幅值较小,所以未在时域响应中清晰显示出来。通过以上分析可知由于TVD-PG传动系统改变了机电传动系统的固有特性,减少了系统的共振区域,同时降低了啮合力的波动幅值,这将有利于降低齿轮系统的动载荷,提高齿轮系统的工作寿命。
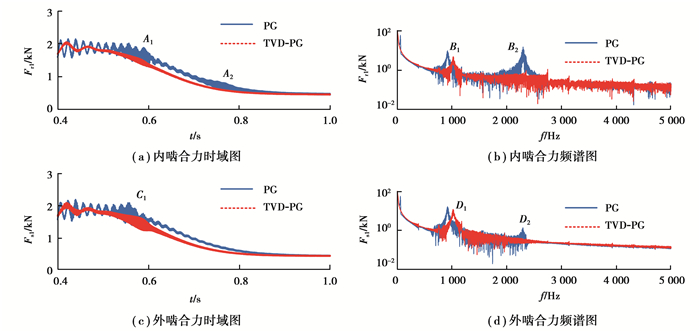
|
图 5 行星齿轮内、外啮合力曲线 Fig. 5 Internal and external meshing force curves |
系统进入稳定工况时,电机电磁转矩Te曲线和行星齿轮内啮合力Fr1曲线如图 6所示,分别表示电机部分和齿轮传动部分的响应特性,同时与传统的电机行星齿轮系统进行了对比。由图 6(a)可看到稳态时TVD-PG系统对电磁转矩的影响与传统的行星齿轮传动没有较大区别,改变并不明显。但图 6(b)表明TVD-PG系统可以有效降低稳态时齿轮系统内啮合力的波动幅值,减小齿轮系统动载荷。虽然已进入稳态,但系统依旧受到内部激励的作用,进而表现出一种动态的稳定状态。
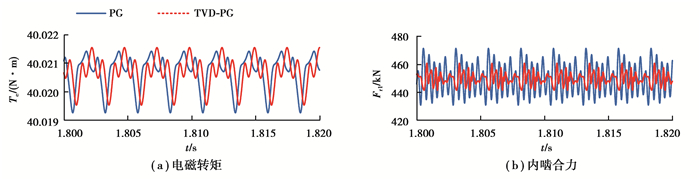
|
图 6 稳态响应曲线 Fig. 6 Steady state response curves |
振动、噪声是齿轮系统重要的动力学特性,由于电机和齿轮系统的耦合作用,齿轮系统的振动必将对电机部分造成一定的影响,这也是产生图 6(a)现象的原因。为了分析这种激励特性,图 7给出了电机-TVD-PG系统稳定时电机电磁转矩Te和电机转速ωm的频谱图,两图中均可以清晰观察到行星齿轮时变啮合刚度的激励频率成分fm,2fm,3fm,4fm,…,且为各频谱图中的主要频率成分。因此机电系统间的耦合作用在实际情况中应予以充分考虑,同时可利用这一特性,通过电机中便于检测的电信号来识别齿轮系统的工作状态或进行故障检测等。
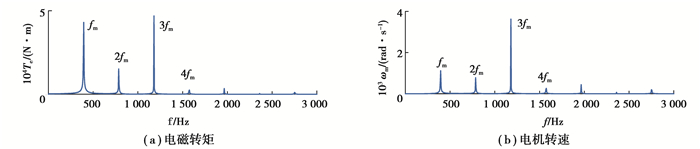
|
图 7 电机响应频谱图 Fig. 7 Motor response spectrums |
为了改善内、外部激励下机电传动系统的动态响应特性,提出了一种新型自减振行星传动形式(TVD-PG传动系统),采用扭转减振装置取代传统行星齿轮中某一构件与箱体固连的方式。并以扭转减振装置耦合内齿圈为例,建立了适用于变速工况下的电机-TVD-PG耦合系统的动力学模型。修改了行星齿轮时变啮合刚度模型,将其表示为关于太阳轮实际角位移的函数,啮合频率随转速实时变化。基于MATLAB/Simulink平台进行仿真,对比传统的电机行星齿轮系统仿真结果,得出如下结论:
1) 在启动过程中,TVD-PG传动系统大幅降低电机电磁转矩的波动,使电机和输出端转速较平稳地增长,电机和齿轮系统可以更快达到稳定状态。同时大幅度减小启动过程中行星齿轮内、外啮合力的波动幅值,并减少系统升速过程中的共振区域,有助于降低齿轮系统动载荷。
2) 在达到稳定时,系统依旧受到内部激励的作用,进而表现出一种动态稳定的状态。由于机电耦合作用的影响,在电机响应曲线中可以清晰观察到行星齿轮时变刚度激励的频率成分。TVD-PG对电机电磁转矩的影响不明显,但可以有效降低机电传动系统稳定时齿轮系统啮合力的波动幅值,改善齿轮啮合状况。
| [1] |
李哲, 郑玲, 胡一明, 等. 轮毂驱动电动汽车振动负效应及抑制方法[J]. 重庆大学学报, 2019, 42(2): 20-29. Li Z, Z L, Hu Y M, et al. Negative vibration effects of in-wheel motor electric vehicles and the method for suppressing them[J]. Journal of Chongqing University, 2019, 42(2): 20-29. (in Chinese) |
| [2] |
卜忠红, 刘更, 吴立言. 行星齿轮传动动力学研究进展[J]. 振动与冲击, 2010, 29(9): 161-166. Pu Z H, Liu G, Wu L Y. Research advances in planetary gear trains dynamics[J]. Vibration and Shock, 2010, 29(09): 161-166. (in Chinese) |
| [3] |
丁闯, 张兵志, 冯辅周, 等. 行星轮系动力学仿真分析与故障诊断[J]. 噪声与振动控制, 2017, 37(4): 144-149. Ding C, Zhang B Z, Feng F Z, et al. Dynamic simulation and fault diagnosis of planetary gear systems[J]. Noise and Vibration Control, 2017, 37(4): 144-149. (in Chinese) |
| [4] |
Khabou M T, Bouchaala N, Chaari F, et al. Study of a spur gear dynamic behavior in transient regime[J]. Mechanical Systems and Signal Processing, 2011, 25(8): 3089-3101. DOI:10.1016/j.ymssp.2011.04.018 |
| [5] |
Haris A, Motato E, Theodossiades S, et al. A study on torsional vibration attenuation in automotive drivetrains using absorbers with smooth and non-smooth nonlinearities[J]. Applied Mathematical Modelling, 2017, 46: 674-690. DOI:10.1016/j.apm.2016.09.030 |
| [6] |
Wand Y, Qin X, Huang S, et al. Design and analysis of a multi-stage torsional stiffness dual mass flywheel based on vibration control[J]. Applied Acoustics, 2016, 104: 172-181. DOI:10.1016/j.apacoust.2015.11.004 |
| [7] |
Hu J, Qin D, Zhao Y, et al. Study on natural torsional vibration characteristics of dual mass flywheel-radial spring type torsional vibration damper[J]. China Mechanical Engineering, 2008, 19(15): 1800-1805. |
| [8] |
Bai W, Qin D, Wang Y, et al. Dynamic characteristics of motor-gear system under load saltations and voltage transients[J]. Mechanical Systems and Signal Processing, 2018, 100: 1-16. DOI:10.1016/j.ymssp.2017.07.039 |
| [9] |
Yi Y, Qin D, Liu C. Investigation of electromechanical coupling vibration characteristics of an electric drive multistage gear system[J]. Mechanism and Machine Theory, 2018, 121: 446-459. DOI:10.1016/j.mechmachtheory.2017.11.011 |
| [10] |
Ge S, Qin D, Hu M, et al. Research on dynamic load characteristics and active control strategy of electro-mechanical coupling powertrain of drum shearer cutting unit under impact load[J]. Journal of Vibroengineering, 2017, 19(3): 1882-1900. DOI:10.21595/jve.2016.17525 |
| [11] |
Guo R, Wang M J. Active control of hybrid electric vehicle launch vibration in pure electric mode[J]. Journal of Vibration and Control, 2018, 24(4): 673-681. DOI:10.1177/1077546316648811 |
| [12] |
Kahraman A. Natural modes of planetary gear trains[J]. Journal of Sound and Vibration, 1994, 173(1): 125-130. DOI:10.1006/jsvi.1994.1222 |
| [13] |
Jian L, Parker R G. Analytical characterization of the unique properties of planetary gear free vibration[J]. Journal of Vibration & Acoustics, 1999, 121(3): 316-321. |
| [14] |
Lin J, Parker R G. Sensitivity of planetary gear natural frequencies and vibration modes to model parameters[J]. Journal of Sound and Vibration, 1999, 228(1): 109-128. DOI:10.1006/jsvi.1999.2398 |
| [15] |
Chaari F, Abbes M S, Rueda F V, et al. Analysis of planetary gear transmission in non-stationary operations[J]. Frontiers of Mechanical Engineering, 2013, 8(1): 88-94. DOI:10.1007/s11465-013-0361-8 |
| [16] |
刘文, 刘君, 林腾蛟, 等. 风电齿轮箱传动误差分析及振动噪声预估[J]. 重庆大学学报, 2017, 40(3): 12-23. Liu W, Liu J, Lin T J, et al. Transmission error analysis and vibration noise prediction of wind power gearbox[J]. Journal of Chongqing University, 2017, 40(3): 12-23. (in Chinese) |
| [17] |
林腾蛟, 曹洪, 吕和生. 4级行星齿轮箱振动噪声预估及修形效果分析[J]. 重庆大学学报, 2018, 41(2): 1-9. Lin T J, Cao H, Lyu H S. Vibration noise prediction and tooth modification effect analysis of a four-stage planetary gearbox[J]. Journal of Chongqing University, 2018, 41(2): 1-9. (in Chinese) |
| [18] |
周志刚, 秦大同, 杨军, 等. 变载荷下风力发电机行星齿轮传动系统齿轮-轴承耦合动力学特性[J]. 重庆大学学报, 2012, 35(12): 7-14. Zhou Z G, Qin D T, Yang J, et al. Gear-bearing coupling dynamic characteristics of wind turbine planetary gear transmission system under variable load[J]. Journal of Chongqing University, 2012, 35(12): 7-14. (in Chinese) |
| [19] |
Liu C, Qin D, Lim T C, et al. Dynamic characteristics of the herringbone planetary gear set during the variable speed process[J]. Journal of Sound and Vibration, 2014, 333(24): 6498-6515. |
| [20] |
潘博, 孙京, 于登云, 等. 直齿行星齿轮动力学建模与分析研究[J]. 动力学与控制学报, 2018, 16(2): 121-128. Pan B, Sun J, Yu D Y, et al. Dynamic modeling and analysis of spur planetary gear[J]. Journal of Dynamics and Control, 2018, 16(2): 121-128. (in Chinese) |
 2021, Vol. 44
2021, Vol. 44



