摆线针轮行星传动具有传动比大、传动精度高、结构紧凑、扭转刚度高和传动效率高等突出优点,被广泛应用于工业机器人、化工、冶金等领域[1-3]。摆线齿廓的精度是影响其传动精度的主要因素,采用金刚石滚轮修整技术的成形磨削法不仅加工效率和精度高,而且可实现摆线齿廓的任意修形,已经成为摆线齿廓精加工的主流方法[4-5]。
高精度复杂形面金刚石滚轮一般采用内电镀法制造[6],滚轮阴模基体形面是金刚石颗粒的定位基准面,其形面精度是影响滚轮最终制造精度的关键因素[7-8]。金属阴模基体在数控精密磨床上加工,对于摆线金刚石滚轮阴模基体的数控磨削加工,由于基体形面曲线复杂,必须用直线或圆弧段逼近原曲线[9],为了提高其数控加工精度,插补算法的研究至关重要。
张敬东等[10]提出了一种等误差直线插补算法用于摆线齿廓的数控加工; 姚必强等[11]提出用等弧长圆弧拟合任意非圆曲线;CAD/CAM方法也广泛应用于复杂非圆曲线的数控加工,该方法的刀具路径由许多细小的直线或圆弧段组成[12-13]。用上述方法拟合复杂非圆曲线,当需要较高的插补精度时,插补节点数量多,且刀具路径不具备G1连续性。采用双圆弧插补法能有效解决上述问题,刘涛等[14-15]采用最优切向量双圆弧插补算法完成涡旋型线零件的数控加工,但该方法需要根据曲线能量极小条件计算最优切向量,计算量大,拟合效率较低。
笔者基于双圆弧插补法,求解出摆线滚轮阴模基体形面曲线方程,建立摆线滚轮阴模基体步长伸缩双圆弧插补数学模型,利用MATLAB软件求解插补节点数据,并进行误差分析,通过控制步长伸缩来调整插补误差。最后通过计算实例验证了该模型的可行性,在相同允差要求下可以提高加工效率,插补数据拟合的加工仿真曲线光滑平整,刀具路径具备G1连续性,插补节点数据导入数控机床即可用于数控程序编制。
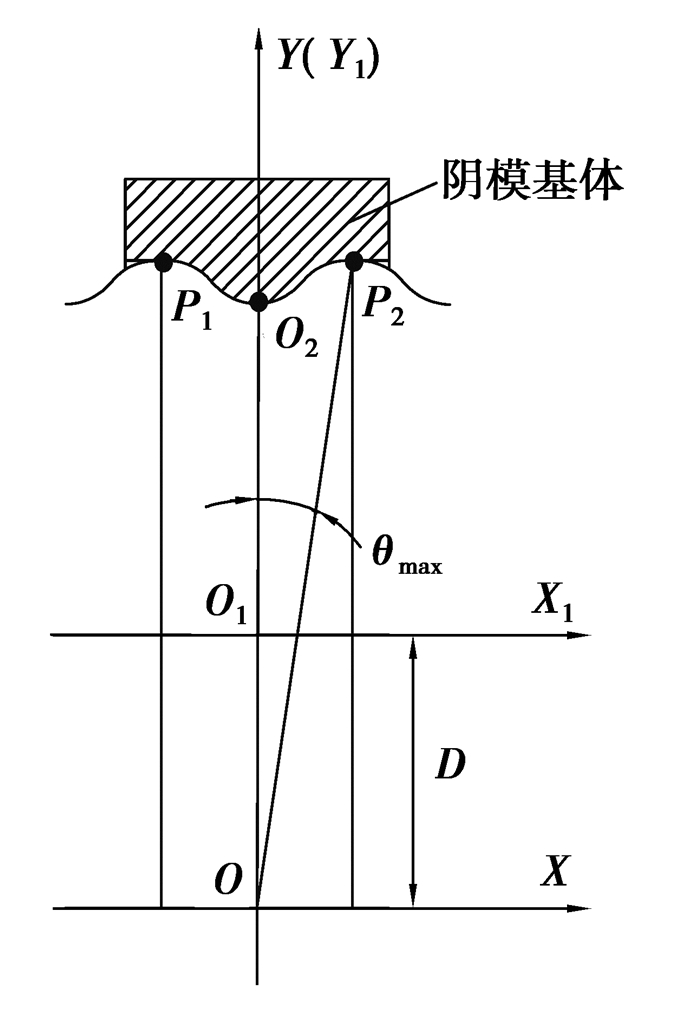
1 摆线滚轮阴模基体形面曲线方程摆线滚轮阴模基体加工坐标系如图 1所示,阴模基体加工坐标系为O1-X1Y1,摆线齿廓坐标系为O-XY,O1X1轴线与OX轴线的距离为D。摆线滚轮阴模基体形面曲线除P1O2P2段外皆为过渡圆弧及直线段,P1O2P2段曲线与摆线齿廓曲线形状相同,且P1O2段曲线与O2P2段曲线关于Y1轴左右对称,因此只需对阴模基体形面O2P2段曲线进行双圆弧插补计算。
|
图 1 摆线滚轮阴模基体加工坐标系 Fig. 1 Machining coordinate system of female mold workpiece |
O2P2段形面曲线在摆线齿廓坐标系中的曲线方程式为:
| $\left\{\begin{array}{l} x=\left(R_{\rm{z}}+\Delta R_{\rm{z}}\right) \sin \theta-e \sin \left(z_{\mathrm{b}} \theta\right)+\left(r_{\rm{z}}+\Delta r_{\rm{z}}\right) \cos \gamma, \\ y=\left(R_{\rm{z}}+\Delta R_{\rm{z}}\right) \cos \theta-e \cos \left(z_{\mathrm{b}} \theta\right)+\left(r_{\rm{z}}+\Delta r_{\rm{z}}\right) \sin \gamma, \\ \sin \gamma=\frac{\cos \theta-K \cos \left(z_{\mathrm{b}} \theta\right)}{\sqrt{1+K^2-2 K \cos \left(z_{\mathrm{g}} \theta\right)}}, \\ \cos \gamma=\frac{K \sin \left(z_{\mathrm{b}} \theta\right)-\sin \theta}{\sqrt{1+K^2-2 K \cos \left(z_{\mathrm{g}} \theta\right)}}。\end{array}\right.$ | (1) |
式中:Rz为针轮中心圆半径;e为偏心距;zb为针轮齿数;zg为摆线轮齿数;rz为针齿半径;ΔRz为移距修形量;Δrz为等距修形量;K=ezb/(Rz+ΔRz);θ∈[0, θmax];θmax=π/zg。
对O2P2段形面曲线在摆线齿廓坐标系中的曲线方程式进行双圆弧插补计算后,通过简单的平移变换矩阵即可将插补节点数据转换到阴模基体加工坐标系中,再将数据导入数控机床便可完成数控加工程序的编制。
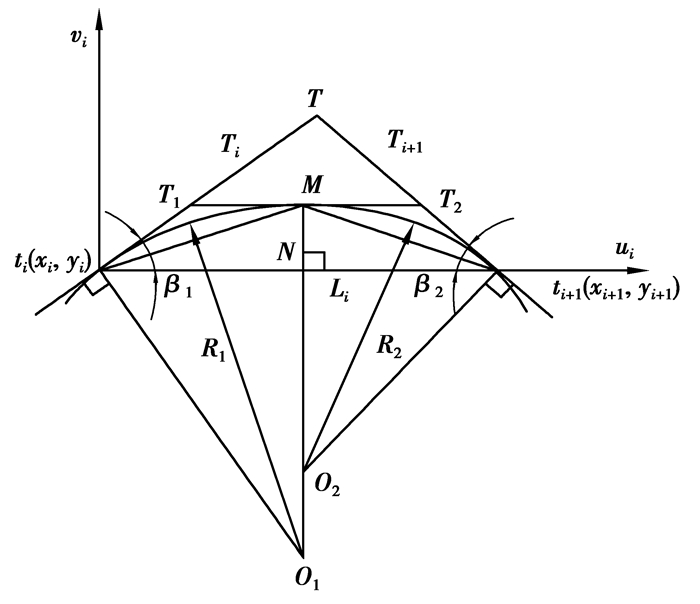
2 摆线滚轮阴模基体步长伸缩双圆弧插补数学模型 2.1 双圆弧插补原理图 2为双圆弧插补原理图,在加工曲线上任取相邻2点ti(xi, yi)、ti+1(xi+1, yi+1),Ti、Ti+1分别为曲线上点ti、ti+1的切矢,过ti、ti+1 2点沿切矢方向作两线段相交于点T得到△titi+1T,△titi+1T的内心是图 2中的M点。

|
图 2 双圆弧插补原理 Fig. 2 Principle of double arc interpolation |
过ti、ti+1点分别作线段tiT、ti+1T的垂线,同时过M点作线段titi+1的垂线与上述2条垂线交于O1、O2点。以O1点为圆心,O1ti为半径作圆弧,圆弧起点为ti,终点为M;同理以O2为圆心、O2ti+1为半径确定另一段起点为ti+1、终点为M的圆弧,由此确定了复杂曲线上任意相邻2点间的插补双圆弧段[16]。
两段圆弧均通过△titi+1T内心M点只需证明
由三角形内心性质可知,Mti为∠Ttiti+1的角平分线,同理Mti+1是∠Tti+1ti的角平分线。过内心M点作线段titi+1的平行线与线段tiT、ti+1T分别交于T1、T2点,由于T1T2//titi+1,Mti平分∠Ttiti+1,所以∠T1tiM=∠T1Mti,故
当完成ti与ti+1 2点间双圆弧插补计算后,继续进行下一相邻2节点ti+1、ti+2间的计算,Ti+1、Ti+2分别为原加工曲线上点ti+1、ti+2的切矢,设ti+1与ti+2 2点间插补圆弧段对应的圆心分别为O3、O4。由以上双圆弧插补原理分析可知,圆心O2对应的圆弧与切矢Ti+1相切于ti+1点,圆心O3对应的圆弧同样与切矢Ti+1相切于ti+1点,故不仅相邻节点ti、ti+1间插补的双圆弧段具有公共切向量,而且同一节点ti+1两侧的圆弧段在节点ti+1处也具有公共切向量Ti+1。因此当采用双圆弧法插补摆线滚轮阴模基体形面曲线时,插补的圆弧段在任意连接点处均有公共切向量,刀具路径具有G1连续性。
2.2 双圆弧半径及公切点坐标参数计算在图 2中,设整体坐标系为o-xy,o-xy是固定坐标系;局部坐标系为ti-uivi,ti-uivi是动坐标系。在o-xy坐标系中,设线段tiT、ti+1T与x轴的夹角为γi、γi+1,线段titi+1与x轴的夹角为θi,线段titi+1的弦长为Li。
γi及γi+1的值可以通过切矢Ti、Ti+1求得,由阴模基体形面曲线方程式(1)可求得Ti、Ti+1,故有
| $\gamma_i=\arctan \left[\frac{-\left(R_{\rm{z}}+\Delta R_{\rm{z}}\right) \sin \theta_i+e z_{\rm{b}} \sin \left(z_{\rm{b}} \theta_i\right)}{\left(R_{\rm{z}}+\Delta R_{\rm{z}}\right) \cos \theta_i-e z_{\rm{b}} \cos \left(z_{\rm{b}} \theta_i\right)}\right], $ | (2) |
| $\gamma_{i+1}=\arctan \left[\frac{-\left(R_{\rm{z}}+\Delta R_{\rm{z}}\right) \sin \theta_{i+1}+e z_{\mathrm{b}} \sin \left(z_{\mathrm{b}} \theta_{i+1}\right)}{\left(R_{\mathrm{z}}+\Delta R_{\mathrm{z}}\right) \cos \theta_{i+1}-e z_{\mathrm{b}} \cos \left(z_{\mathrm{b}} \theta_{i+1}\right)}\right] 。$ | (3) |
线段titi+1与x轴的夹角为
| $\theta_i=\arctan \left(\frac{y_{i+1}-y_i}{x_{i+1}-x_i}\right) 。$ | (4) |
线段titi+1的弦长为
| $L_i=\sqrt{\left(y_{i+1}-y_i\right)^2+\left(x_{i+1}-x_i\right)^2}。$ | (5) |
设点M在坐标系o-xy、ti-uivi中的坐标矢量分别为(xM, yM, 1)T、(uM, vM, 1)T,局部坐标系到整体坐标系的变换矩阵为M0 i,可求得
| $\boldsymbol{M}_{0 i}=\left[\begin{array}{ccc} \cos \theta_i & -\sin \theta_i & x_i \\ \sin \theta_i & \cos \theta_i & y_i \\ 0 & 0 & 1 \end{array}\right]。$ | (6) |
局部坐标系中的坐标矢量可通过变换矩阵M0i转换到整体坐标系中
| $\left(x_M, y_M, 1\right)^{\mathrm{T}}=\boldsymbol{M}_{0 i}\left(u_M, v_M, 1\right)^{\mathrm{T}}。$ | (7) |
如图 3所示,局部坐标系ti-uivi中,由内心几何性质可知,Mti平分∠Ttiti+1(图中β1),Mti+1平分∠T ti+1ti (图中β2)。
|
图 3 双圆弧坐标计算 Fig. 3 Double arc coordinate calculation |
在△titi+1T中,内角β1、β2为
| $\beta_1=\gamma_i-\theta_i, $ | (8) |
| $\beta_2=\pi-\left(\gamma_{i+1}-\theta_i\right)。$ | (9) |
在△titi+1M中,由正弦定理可以推出
| $l_{t i M}=\frac{\sin \left(\beta_2 / 2\right) L_i}{\sin \left[\left(\beta_1+\beta_2\right) / 2\right]}。$ | (10) |
由于∠MNti、∠TtiO1均为90°,可以求出
| $l_{t i N}=l_{t_i M} \cos \left(\beta_1 / 2\right), $ | (11) |
| $l_{M N}=l_{t_i M} \sin \left(\beta_1 / 2\right) , $ | (12) |
| $l_{N O_1}=\frac{l_{t i N}}{\tan \beta_1}, $ | (13) |
| $l_{{NO} 2}=\frac{L_i-l_{t_i \mathrm{~N}}}{\tan \beta_2}。$ | (14) |
因此在局部坐标系下,可以求出公切点M坐标为
| $\left\{ \begin{array}{l} {u_M} = \frac{{\sin \left( {{\beta _2}/2} \right)\cos \left( {{\beta _1}/2} \right){L_i}}}{{\sin \left[ {\left( {{\beta _1} + {\beta _2}} \right)/2} \right]}}, \\ {v_M} = \frac{{\sin \left( {{\beta _2}/2} \right)\sin \left( {{\beta _1}/2} \right){L_i}}}{{\sin \left[ {\left( {{\beta _1} + {\beta _2}} \right)/2} \right]}}。\end{array} \right.$ | (15) |
圆心O1、O2坐标分别为
| $\left\{ \begin{array}{l} {u_{{O_1}}} = \frac{{\sin \left( {{\beta _2}/2} \right)\cos \left( {{\beta _1}/2} \right){L_i}}}{{\sin \left[ {\left( {{\beta _1} + {\beta _2}} \right)/2} \right]}}, \\ {v_{{O_1}}} = \frac{{\sin \left( {{\beta _2}/2} \right)\cos \left( {{\beta _1}/2} \right){L_i}}}{{\sin \left[ {\left( {{\beta _1} + {\beta _2}} \right)/2} \right]\tan {\beta _1}}}; \end{array} \right.$ | (16) |
| $\left\{ \begin{array}{l} u_{O_2} =\frac{\sin \left(\beta_2 / 2\right) \cos \left(\beta_1 / 2\right) L_i}{\sin \left[\left(\beta_1+\beta_2\right) / 2\right]} ,\\ v_{O_2} =-\left[L_i-\frac{\sin \left(\beta_2 / 2\right) \cos \left(\beta_1 / 2\right) L_i}{\sin \left[\left(\beta_1+\beta_2\right) / 2\right]}\right] / \tan \beta_2 。\end{array} \right.$ | (17) |
两段圆弧半径R1、R2为
| $\left\{\begin{array}{l} R_1=\frac{\sin \left(\beta_2 / 2\right) L_i}{\sin \left[\left(\beta_1+\beta_2\right) / 2\right]}\left[\sin \left(\beta_1 / 2\right)+\cos \left(\beta_1 / 2\right) / \tan \beta_1\right] ; \\ R_2=\frac{\sin \left(\beta_2 / 2\right) L_i}{\sin \left[\left(\beta_1+\beta_2\right) / 2\right]}\left[\sin \left(\beta_1 / 2\right)-\cos \left(\beta_1 / 2\right) / \tan \beta_2\right]+L_i / \tan \beta_2 。\end{array}\right.$ | (18) |
圆弧半径值R1、R2和公切点M及圆心O1、O2在局部坐标系中的坐标值均已计算完毕,通过坐标变换矩阵M0 i即可得到公切点M及圆心O1、O2在整体坐标系中的坐标值。
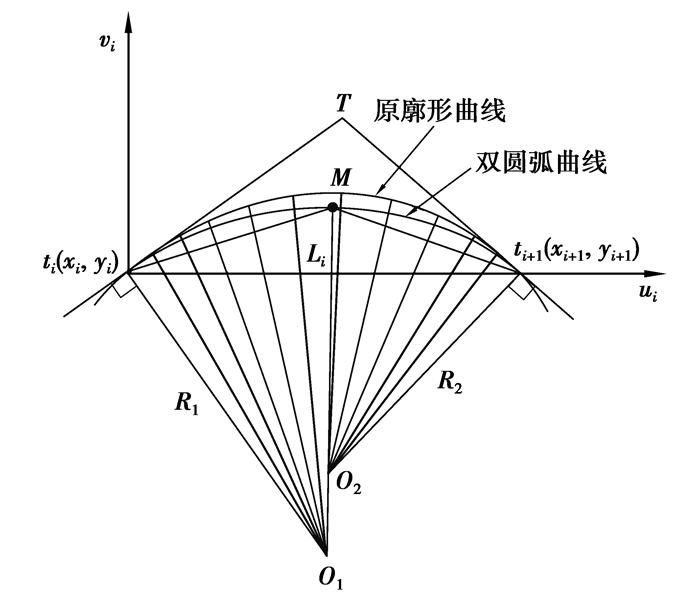
2.3 摆线滚轮阴模基体双圆弧插补误差分析完成两个节点间的插补计算后,需要对产生的插补误差进行分析控制。插补误差的理论值是原廓形曲线上任意点沿其法线方向上与插补圆弧曲线间距离的最大值,在实际应用中可简化计算,取原廓形曲线上任意一点到插补圆弧圆心的距离与两段圆弧半径(R1或R2)之差的最大值为插补误差。
|
图 4 插补误差计算 Fig. 4 Calculation of interpolation error |
上图中Li为两节点ti、ti+1之间的直线距离,将Li等分为N+1段,一般N+1取10到15,将等分点的横坐标转换到整体坐标系中求出摆线滚轮阴模基体形面曲线上的点pj(xj, yj)(j=1, 2, …, N),比较xj与xM(圆弧公切点横坐标值)的大小,当xj≤xM时,原形面曲线被拟合成第一段圆弧,此时的插补误差为
| $\varepsilon_{1 j}=\left|\sqrt{\left(x_j-x_{O_1}\right)^2+\left(y_j-y_{O_1}\right)^2}-R_1\right|, \quad j=1, 2, \cdots, m 。$ | (19) |
式中m是第一段圆弧对应的最后一个等分点,且m<N。
当xj>xM时,原形面曲线被拟合成第二段圆弧,此时的插补误差为
| $\varepsilon_{2 j}=\left|\sqrt{\left(x_j-x_{O_2}\right)^2+\left(y_j-y_{\left.O_2\right)^2}\right.}-R_2\right|, \quad j=m+1, m+2, \cdots, N。$ | (20) |
ε1j与ε2j中的最大值即为这两个节点间的插补误差ε,即
| $\varepsilon=\max \left(\varepsilon_{1 j}, \varepsilon_{2 j}\right)。$ | (21) |
判断任意相邻两节点间的插补误差ε与所允许的插补误差σε的大小,如果ε>σε,缩小步长直至满足ε<σε的要求;而当ε远小于σε时,可适当增大步长使得插补误差小于并接近于插补允差,这就是步长伸缩双圆弧插补算法的实质。
2.4 摆线滚轮阴模基体步长伸缩双圆弧插补算法进行双圆弧插补时,如果插补段曲线凹凸性不一致,会出现S型拟合圆弧。因此曲线上若存在拐点应将曲线分段再进行插值计算。曲率计算公式为
| $k=\frac{\frac{\mathrm{d} x}{\mathrm{~d} \theta} \times \frac{\mathrm{d}^2 y}{\mathrm{~d} \theta}-\frac{\mathrm{d} y}{\mathrm{~d} \theta} \times \frac{\mathrm{d}^2 x}{\mathrm{~d} \theta}}{\left[\left(\frac{\mathrm{d} x}{\mathrm{~d} \theta}\right)^2+\left(\frac{\mathrm{d} y}{\mathrm{~d} \theta}\right)^2\right]^{\frac{3}{2}}} 。$ | (22) |
由曲率k=0求得O2P2段曲线拐点处参数角为
| $\theta_1=\frac{\arccos \left[\left(1+z_{\mathrm{b}} K^2\right) /\left(K+K z_{\mathrm{b}}\right)\right]}{z_{\mathrm{g}}} 。$ | (23) |
因此O2P2段曲线需分为[0, θ1]、[θ1, θmax]两段进行双圆弧插补计算。
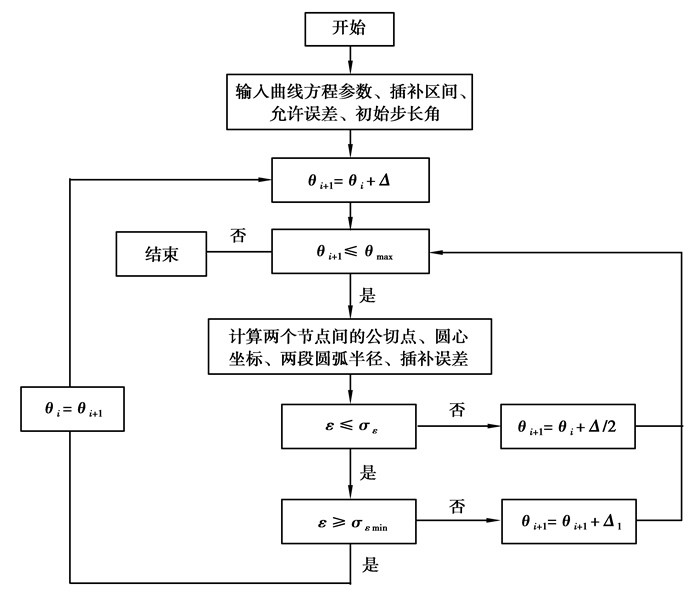
O2P2段曲线的步长伸缩双圆弧插补算法计算步骤如下:
1) 给定初始参数角θ0和初始步长角Δ,计算相邻2节点的坐标ti(xi, yi)和ti+1(xi+1, yi+1)及相应节点处的切矢Ti、Ti+1,由双圆弧插补计算原理求出公切点M、圆心O1、O2点坐标值及相应圆心半径R1、R2的值。
2) 将相邻2节点间的插补误差与插补允差σε比较,同时为了提高加工效率,对插补允差设定一个下限值σεmin。若ε>σε,步长角减小一半调整曲线上节点ti+1的位置重新进行插补计算直至满足误差要求;若ε<σεmin,适当增大步长角使插补误差接近插补允差,当θi≥θmax时,终止计算。
摆线滚轮阴模基体步长伸缩双圆弧插补算法流程如图 5所示。
|
图 5 步长伸缩双圆弧插补算法流程图 Fig. 5 Flow chart of variable-step-double-arc interpolation algorithm |
取40E摆线轮工件参数作为计算实例参数,其中e=1.3,zb=40,zg=39,rz=2.5,Rz=63.7,ΔRz=-0.1,Δrz=0.075,θ∈[0, π/39]。将上述参数代入摆线滚轮阴模基体形面曲线方程式中,根据上节中的插补算法流程在MATLAB软件中编程进行数值计算。
初始参数角θ0=0,初始步长角选取0.001 2 rad,插补允差σε=0.01 μm。以初始步长角等分参数角取相同插补节点数,可以得到69个插补节点。分别采用双圆弧插补法与直线插补法对O2P2段曲线进行插补计算,在O2P2段曲线上随机连续选取8个插补节点,插补误差对比结果如表 1所示。
| 表 1 双圆弧与直线插补误差对比结果 Table 1 Comparison of double arc and linear interpolation error |
当节点数目相同时,表中结果显示直线插补只有最后2个节点之间的插补误差小于插补允差,其他节点间的误差远大于插补允差σε,而双圆弧插补误差均小于插补允差σε。直线插补最小误差为0.009 μm,双圆弧插补最大误差为2.176 nm,双圆弧插补最大误差比直线插补最小误差降低了75%,对比任意节点处得到的数据发现插补误差均降低75%以上。
等步长角得到的双圆弧插补误差曲线如图 6(a)所示,通过分析插补节点的坐标可知,在超过一定参数角后,继续以满足插补误差的步长角插补时,会导致插补节点过于集中,从而插补误差的最值出现数量级的差距,加工程序更加冗长,且加工零件表面质量不均匀。
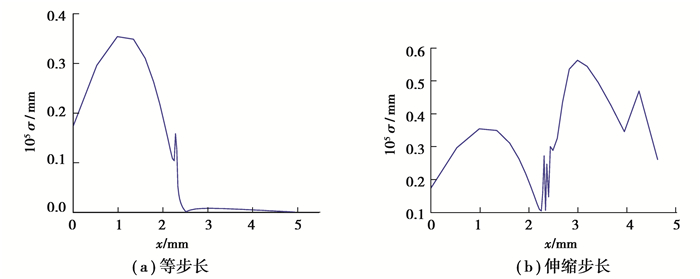
|
图 6 等步长角与伸缩步长角误差曲线对比图 Fig. 6 Comparison of interpolation error curves of equal step angle and telescopic step angle |
采用图 5所示的步长伸缩双圆弧插补算法,对加工允许误差设定一个下限值σεmin=0.001 μm,当插补节点间的误差小于下限值时,适当增加步长角调整节点ti+1在曲线上的位置,使得插补误差小于并接近插补允差。
图 6(b)是控制步长角伸缩后的插补误差曲线图,插补误差均小于插补允差σε。在满足同一插补允差时,等步长角的插补节点数为69个,控制步长角伸缩后插补节点数为30个,节点数目减少了55%,插补的圆弧段也减少了55%。因此在相同插补允差要求下控制步长角伸缩可以提高摆线滚轮阴模基体工件的加工效率,同时可以保证加工表面质量均匀。
图 7曲线是由步长伸缩双圆弧插补节点数据拟合的O2P2段加工仿真曲线,由于拟合的圆弧段在每个离散点处都有公共切向量,因此拟合曲线一阶导数连续,拟合曲线表面光滑平整,刀具路径具有G1连续性,保证了工件的加工质量。
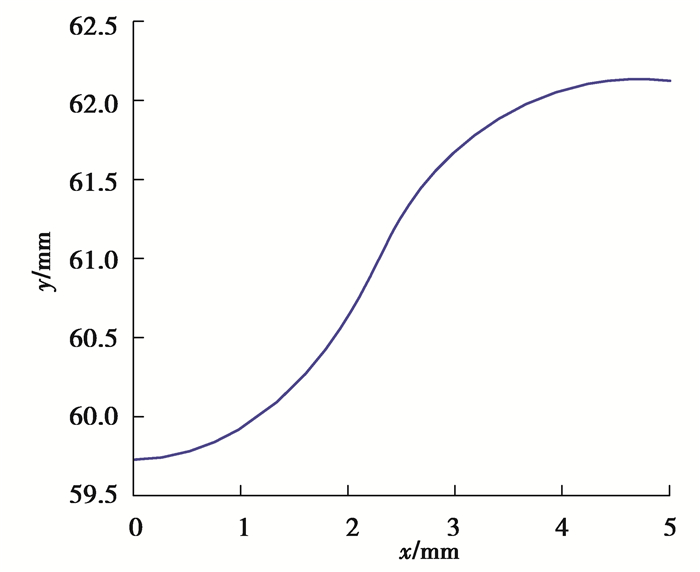
|
图 7 O2P2段曲线加工仿真图 Fig. 7 Processing simulation diagram of O2P2 curve |
以摆线金刚石滚轮阴模基体为加工对象,基于双圆弧插补法,建立了摆线滚轮阴模基体步长伸缩双圆弧插补数学模型,该模型插补点求解方便,控制步长伸缩可以调整插补误差。对该数学模型进行实例计算及仿真,得出结论如下:
1) 双圆弧插补误差小于0.01 μm,在节点数相同时其插补误差比直线插补误差降低75%,满足摆线滚轮阴模基体高精度加工要求。
2) 控制步长伸缩,在同精度允差下拟合圆弧段数减少55%,可以提高摆线滚轮阴模基体工件的加工效率。
3) 由插补算法原理及插补数据拟合的加工仿真曲线可知,插补的任意相邻圆弧段彼此相切,拟合曲线表面光滑连续,刀具路径具备G1连续性。
| [1] |
Pham A D, Ahn H J. High precision reducers for industrial robots driving 4th industrial revolution: state of arts, analysis, design, performance evaluation and perspective[J]. International Journal of Precision Engineering and Manufacturing-Green Technology, 2018, 5(4): 519-533. DOI:10.1007/s40684-018-0058-x |
| [2] |
Wang H, Shi Z Y, Yu B, et al. Transmission performance analysis of RV reducers influenced by profile modification and load[J]. Applied Sciences, 2019, 9(19): 4099. DOI:10.3390/app9194099 |
| [3] |
张也, 李朝阳, 黄健. 多因素综合作用的摆线针轮传动误差分析[J]. 重庆大学学报, 2020, 43(12): 1-12. Zhang Y, Li C Y, Huang J. Transmission error analysis of cycloidal pinwheel based on multi-factor comprehensive effect[J]. Journal of Chongqing University, 2020, 43(12): 1-12. (in Chinese) DOI:10.11835/j.issn.1000-582X.2020.12.001 |
| [4] |
张跃明, 杨申春, 纪姝婷, 等. RV减速器摆线轮磨削工艺研究[J]. 机床与液压, 2018, 46(15): 28-31, 36. Zhang Y M, Yang S C, Ji S T, et al. Grinding technology research of RV reducer cycloid gear[J]. Machine Tool & Hydraulics, 2018, 46(15): 28-31, 36. (in Chinese) DOI:10.3969/j.issn.1001-3881.2018.15.007 |
| [5] |
张德泉, 李真, 曹克伟, 等. 摆线轮齿廓曲线CNC成形磨削机理[J]. 天津大学学报, 1998, 31(4): 71-75. Zhang D Q, Li Z, Cao K W, et al. Study on the CNC profiling gear grinding method of epicycloidal gear[J]. Journal of Tianjin University, 1998, 31(4): 71-75. (in Chinese) |
| [6] |
Cui Z M, Liu Z R, Zhang H Y. Manufacturing technique of high precision intricate diamond dressing roller[J]. Materials Science Forum, 2006, 532-533: 492-495. DOI:10.4028/www.scientific.net/MSF.532-533.492 |
| [7] |
杨摩西, 崔仲鸣, 赫青山, 等. 轴承滚道磨削中金刚石滚轮修整技术的应用[J]. 轴承, 2019(3): 15-19. Yang M X, Cui Z M, He Q S, et al. Application of diamond roller dressing technology in grinding of bearing raceway[J]. Bearing, 2019(3): 15-19. (in Chinese) |
| [8] |
Wu M L, Ren C Z, Zhang K F. ELID groove grinding of ball-bearing raceway and the accuracy durability of the grinding wheel[J]. The International Journal of Advanced Manufacturing Technology, 2015, 79(9/10/11/12): 1721-1731. |
| [9] |
Yang J X, Ai W, Liu Y X, et al. Kinematics model and trajectory interpolation algorithm for CNC turning of non-circular profiles[J]. Precision Engineering, 2018, 54: 212-221. DOI:10.1016/j.precisioneng.2018.05.014 |
| [10] |
张敬东. 摆线齿轮的数控加工[J]. 现代制造工程, 2005(3): 49-50. Zhang J D. Numerical control machining of hypocycloidal gears[J]. Machinery Manufacturing Engineer, 2005(3): 49-50. (in Chinese) |
| [11] |
姚必强, 姚进. 数控加工曲线的等弧长圆弧拟合方法[J]. 四川大学学报(工程科学版), 2008, 40(1): 171-174. Yao B Q, Yao J. The method of curve fitting with equal length arc used for NC processing[J]. Journal of Sichuan University (Engineering Science Edition), 2008, 40(1): 171-174. (in Chinese) |
| [12] |
Ji S J, Lei L G, Zhao J, et al. An adaptive real-time NURBS curve interpolation for 4-axis polishing machine tool[J]. Robotics and Computer-Integrated Manufacturing, 2021, 67: 102025. |
| [13] |
Knez M, Žagar E. Interpolation of circular arcs by parametric polynomials of maximal geometric smoothness[J]. Computer Aided Geometric Design, 2018, 63: 66-77. |
| [14] |
Wu Z X, Liu T. A double circular arc fitting algorithm for CNC machining of non-uniform scroll components[J]. The International Journal of Advanced Manufacturing Technology, 2019, 104(9/10/11/12): 4485-4495. |
| [15] |
刘涛, 李亚军. 三段基圆渐开线涡旋型线的双圆弧插值算法拟合与加工[J]. 现代制造工程, 2018(8): 109-114. Liu T, Li Y J. Fitting and processing of double circular arc interpolation algorithm for three section base circle involute profile[J]. Modern Manufacturing Engineering, 2018(8): 109-114. (in Chinese) |
| [16] |
孙永吉, 刘涛, 唐林虎, 等. 立铣变截面涡旋齿组合型线的插补研究[J]. 化工机械, 2019, 46(1): 35-40. Sun Y J, Liu T, Tang L H, et al. Study of profiles of variable cross-section scroll interpolation for end milling[J]. Chemical Engineering & Machinery, 2019, 46(1): 35-40. (in Chinese) |
 2022, Vol. 45
2022, Vol. 45


