据统计,单相接地故障在配电网的各类故障中占80%以上[1],该故障会恶化设备绝缘保护,引起短路故障甚至断电危险,危害人身和财产安全。因此,高效、精确的配电网故障识别及定位对维系电网安全有着重要意义[2]。
在现代化智能电网中,配电网故障定位主要依靠线路端点的馈线终端装置(feeder terminal unit, FTU)监测并上传故障数据[3]。故障定位方法可分为直接法[4]和间接法[5-8]。直接法主要为矩阵法,该方法原理简单、定位迅速,但在DG接入配电网后由于拓扑结构发生改变,无法继续保持良好的定位性能[4]。间接法方法众多,且包含各类智能算法。文献[5]测量线路两端的暂态零序电流并串接成特征波形,利用一维CNN自适应地提取特征波形特征。文献[6]根据行波传播特性和配电网拓扑结构建立并比较固有距离差矩阵和故障距离差矩阵的差异,采用故障分支判断矩阵和横向指数Q进行故障定位。文献[7]利用一种改进的动态时间规整方法,通过在重合叠加行波数据库中寻找最相似的信号来识别故障区段。以上方法都未对模型能否适用于含DG配电网进行讨论,因此无法直接应用于有源配电网。随着光伏电站等分布式电源(distribute generator, DG)大量接入配电网系统,配电网单一的集中式供电结构发生改变,拓扑结构和潮流方向更为复杂[8],传统的故障定位方法已不再适用于有源配电网,因此,如何快速精准地实现有源配电网故障定位成为目前的研究焦点。
近年来,出现了适用于有源配电网故障定位新算法的有益探索。文献[9]将BP神经网络方法应用于配电网支路电压和电流的模式识别,但在DG发生改变时矩阵无法继续保持良好性能。文献[10]根据故障时各支路波头计算TDOA矩阵,分析前后TDOA差值实现故障定位,该方法仅参考行波信号信息,不受保护信息的影响,但其原始特征矩阵特征量较多,对于复杂有源配电网来说定位效率不高。文献[11]以故障电压为特征量,支持向量机(support vector machine, SVM)为分类器,通过线性判别分析(linear discriminant analysis, LDA)提取故障特征,其特征分类思想能与配电网故障定位较好匹配,由此文中对其LDA分类判据有一定继承。
当有源配电网发生故障时,故障态与非故障态的相电压、相电流差具有明显的暂态特征[6],因此,文中从故障产生的行波暂态波形与故障发生位置的相关性入手,通过分析故障线模行波小波特征值,以LDA为判据进行特征降维,并与基于径向基函数(radial basis function, RBF)核的朴素贝叶斯分类(naive Bayesian classifier, NBC)算法结合,实现含DG的配电网故障区段定位。
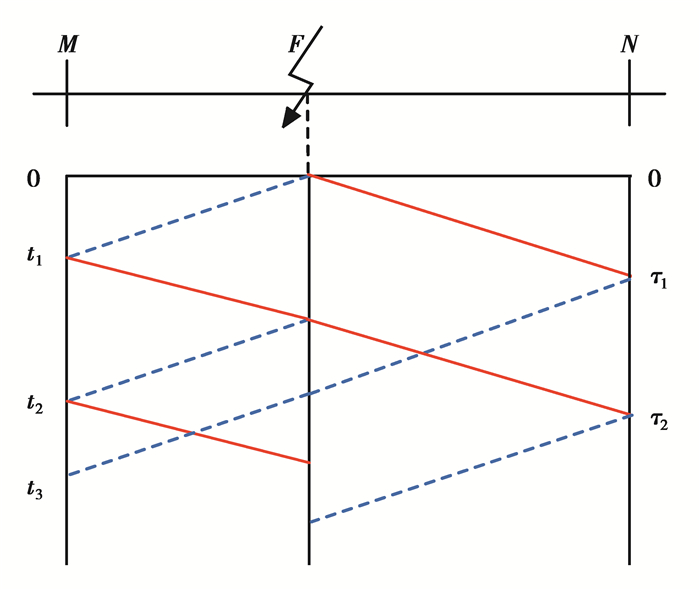
1 行波理论配电线路出现单相接地故障问题时,从叠加原理的角度出发,相当于一个脉冲信号源附加于故障点之上,单相接地故障行波将会沿着线路朝故障点两侧进行传播。结合对行波折射与反射原理的分析,当故障行波在朝故障点两侧进行传播时,若遇到波阻抗不连续点,故障行波将会形成折射与反射,如图 1所示。
|
图 1 行波传播过程 Fig. 1 Propagation process of traveling wave |
图中MN为故障区段,F为单相接地故障点,纵轴为故障发生后的时间。故障产生的正向波由实线表示,反向波由虚线表示。由于配电网中具备众多长度各异的分支线路,行波在传播过程中在不同分支线路位置中形成的反射过程、发射波传播路径等皆存在不同,叠加形成最终的故障行波。时域反射法和行波理论是通过长线模型实现的。沿线路电压方程的解为[12]
| $ \boldsymbol{V}(x)=e^{+x \boldsymbol{\gamma}} \boldsymbol{V}_{+}+e^{-x \boldsymbol{\gamma}} \boldsymbol{V}_{-}, $ | (1) |
| $ \boldsymbol{\gamma}^2=\boldsymbol{Z} \boldsymbol{Y}, $ | (2) |
式中:Z和Y是单位线路长度的阻抗和导纳;γ2是传播常数矩阵,其在单相线路中可以使用参数R、L、G和C写成
| $ \gamma=\alpha+j \beta=\sqrt{(R+j L \omega)(G+j C \omega)}, $ | (3) |
式中:α是衰减常数;β是相位常数。式(1)的e+xγV+是入射波,e-xγV-是反射波。
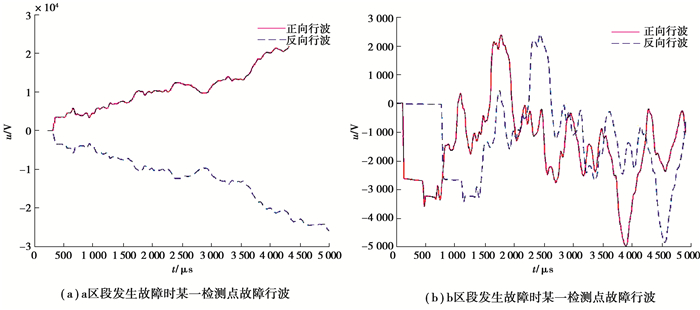
在IEEE 5节点配电网仿真模型中位于不同区段的故障点发生故障时,同一检测点显示了截然不同的行波波形,如图 2所示。因此故障所在区段可以利用检测点接收的故障行波进行判断。考虑到不同检测点接收到的故障行波存在一定数据特征差异,可寻找特征差异最大的几个检测点的行波特征组成最优故障特征集来确定故障发生的区段。
|
图 2 IEEE 5节点配电网故障区段不同时某一检测点α模行波波形 Fig. 2 α-mode traveling wave waveform of a certain detection point in different fault sections of IEEE 5-bus distribution networks |
当分布式电源并网,大量电力电子设备将接入配电网,其非线性特质将产生大量谐波。高频段的谐波分量只有通过输出滤波器衰减后才能流入交流配电网侧,所以如果只选择高频故障产生的行波信号进行故障定位,电力电子设备产生的谐波对行波信号的影响可以忽略。此外,配电网中每个分支的线路长度相对较短,而故障产生的行波到达网络末端的每个探测器的时间通常为微秒到几十微秒。然而,电力电子设备的控制系统具有响应延迟,通常为毫秒级,远大于行波的传输时间。
所以,在有源配电网中,DG可作为故障行波检测线路的边界。利用检测到的行波信息可以精确定位故障点,现有的配电网行波故障定位方法也可以直接应用于有源配电网[13]。
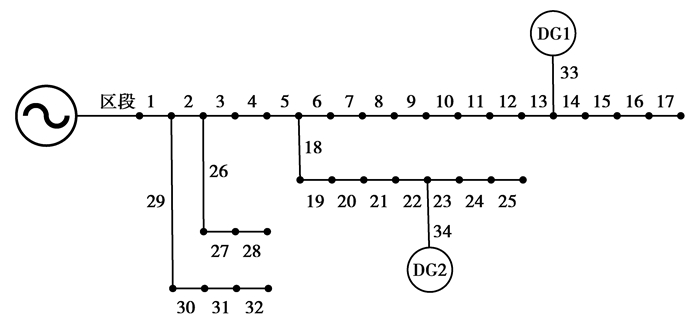
2 故障数据特征提取文中基于Matlab软件搭建如图 3所示的IEEE 33节点含DG的10 kV配电网模型[14]。在该仿真模型的每个节点和DG接入处都设置有检测点,读取故障前后行波数据。DG1和DG2皆为并网逆变型直驱风电机组。
|
图 3 IEEE 33节点含DG配电网模型 Fig. 3 IEEE 33-bus distribution network model with DG |
在该有源配电网模型每一段线路10%~90%区段内每隔10%距离确定一故障点,仿真A相接地故障。对配电线路模型加入故障点后进行数据采样,故障分量取信号故障开始后0.5 ms内三相电压的幅值与故障发生前同一周期的三相电压幅值进行相减得到的电压暂态量,同样方法得到电流暂态量,根据Clark变换矩阵将三相暂态量分解为α、β、0模分量。Clark变换矩阵计算公式为
| $ \left[\begin{array}{l} x_\alpha \\ x_\beta \\ x_0 \end{array}\right]=\frac{1}{3}\left[\begin{array}{ccc} 2 & -1 & -1 \\ 0 & \sqrt{3} & -\sqrt{3} \\ 1 & 1 & 1 \end{array}\right]\left[\begin{array}{l} x_a \\ x_b \\ x_c \end{array}\right], $ | (4) |
式中:xa,xb,xc为相量; xα,xβ,x0为模量。
利用波阻抗计算反向行波的分量进行信号的奇异点检测。波阻抗公式和正反向行波公式分别为
| $ Z_{\mathrm{cm}}=\sqrt{\frac{L_{\mathrm{m}}}{C_{\mathrm{m}}}}, $ | (5) |
| $ \left\{\begin{array}{l} U_{\mathrm{f} \mathtt{α}}=\left(U_{\mathrm{m} 1}+I_{\mathrm{m} 1} Z_{\mathrm{cm}}\right)^{\mathrm{T}}, \\ U_{\mathrm{r} \mathtt{α}}=\left(U_{\mathrm{m} 1}-I_{\mathrm{m} 1} Z_{\mathrm{cm}}\right)^{\mathrm{T}}, \end{array}\right. $ | (6) |
式中:Lm和Cm分别为输电线路单位电感和单位电容;Um1为A相电压;Im1为A相电流;Ufα为正向α模电压;Urα为反向α模电压。
利用小波变换对故障行波电压暂态过程进行分析,其在频域内进行,目的是在已知网络拓扑结构和导线几何结构的情况下,确定可用于推断故障位置的特定频率。选取行波的小波基时,由于Db系列小波[15]拥有紧支性和高阶消失矩,定位性能好,小波分析的计算量较小;且相较同属于正交紧支集小波的Coiflet系列小波、Symlet系列小波又具有频率局部化能力好和时域波形能量集中的优点,故选定Db系列小波。考虑到行波暂态信号需要小波变换在较短的时域内提取准确的故障信息,即小波函数需有较高的能量集中程度和较少的波动次数,而Db系列不同的小波能量集中程度是不同的。表 1为Db3~Db9小波的能量集中程度。
| 表 1 Db3~Db9小波的能量集中程度 Table 1 Energy concentration degree of Db3~Db9 wavelets |
因此选用Db6小波,并对各个检测点故障反向行波α模分量进行小波分解,得到a6和d6-d1共7个频带的小波分解能量,组成故障定位所需要的原始特征矩阵A,则A可表示为
| $ \boldsymbol{A}=\left[\begin{array}{cccc} E_1^1 & E_2^2 & \cdots & E_1^7 \\ E_2^1 & E_2^2 & \cdots & E_2^7 \\ \cdots & \cdots & & \cdots \\ E_{35}^1 & E_{35}^2 & \cdots & E_{35}^7 \end{array}\right], $ | (7) |
式中,Esr表示第s个测量点的第r层小波能量。
在配电网32个线路及DG 2个线路故障区段下得到的多个样本Ali分别组成样本集Ω1, Ω2, …, Ω34,每一个样本都包含原始特征矩阵A中的每一个特征。
| $ \left\{\begin{array}{c} \boldsymbol{\varOmega}_1=\left\{\boldsymbol{A}_1^1, \boldsymbol{A}_2^1, \cdots, \boldsymbol{A}_{N_1}^1\right\}, \\ \boldsymbol{\varOmega}_2=\left\{\boldsymbol{A}_1^2, \boldsymbol{A}_2^2, \cdots, \boldsymbol{A}_{N_2}^2\right\}, \\ \cdots \\ \boldsymbol{\varOmega}_{34}=\left\{\boldsymbol{A}_1^{34}, \boldsymbol{A}_2^{34}, \cdots, \boldsymbol{A}_{N_k}^{34}\right\}, \end{array}\right. $ | (8) |
式中:Ni表示第i类故障样本数;Ali表示第i类样本集中的第l个样本。
3 基于线性判别分析的最优故障特征选择对实际工程中复杂的配电网系统来说,考虑到故障数据特征维数较大,将所有特征用于故障定位是不现实的,因此,需将故障数据降维,挑选出最具代表性的最优故障特征。最优故障特征的选择包括确定最优故障特征维数和在该维数确定情况下选择其最优故障特征。假设故障维数已确定为M维,为了在该维度下从所有故障特征中挑选出最优的特征组合,需选取适合的判据,挑选出最有代表性的M个特征组成一个多维特征。
LDA是一种监督学习的降维技术[16],目前应用广泛。LDA的基本思想是将高维的模式样本投影到最佳鉴别矢量空间,以达到抽取分类信息和压缩特征空间维数的效果,投影后保证模式样本在新的子空间有最大的类间距离和最小的类内距离,即模式在该空间中有最佳的可分离性。LDA作为判据能有效提升同一区段内故障点的关联性。
以下为基于LDA判据的最优M维故障特征选择的具体步骤。
Step 1:从A中取出M个元素共有C35×7M种取法,按照任何一种取法,从A中取出所有含M个元素的特征组,得到M维特征子集ηM={Er1s1, Er2s2, …, ErMsM},由该M维特征子集组成新的样本集
| $ \left\{\begin{array}{c} \boldsymbol{\lambda}_1=\left\{\boldsymbol{A}_1^1, \boldsymbol{A}_2^1, \cdots, \boldsymbol{A}_{N_1}^1\right\}, \\ \boldsymbol{\lambda}_2=\left\{\boldsymbol{A}_1^2, \boldsymbol{A}_2^2, \cdots, \boldsymbol{A}_{N_2}^2\right\}, \\ \cdots \\ \boldsymbol{\lambda}_k=\left\{\boldsymbol{A}_1^k, \boldsymbol{A}_2^k, \cdots, \boldsymbol{A}_{N_k}^k\right\} 。\end{array}\right. $ | (9) |
Step 2:令μi为第i类样本的平均值,μ为所有样本的平均值,则
| $ \left\{\begin{array}{c} \boldsymbol{\mu}_i=\frac{1}{n_i} \sum_{l=1}^{n_i} \boldsymbol{A}_l^i, \\ \boldsymbol{\mu}=\frac{1}{n} \sum_{i=1}^m \sum_{l=1}^{n_i} \boldsymbol{A}_l^i。\end{array}\right. $ | (10) |
其中, ni为第i类样本数,n为总样本数。构造类内离散度SB和类间离散度SW:
| $ \left\{\begin{array}{c} \boldsymbol{S}_{\mathrm{B}}=\frac{1}{n} \sum_{i=1}^m n_i\left(\boldsymbol{\mu}_i-\boldsymbol{\mu}\right)\left(\boldsymbol{\mu}_i-\boldsymbol{\mu}\right)^{\mathrm{T}}, \\ \boldsymbol{S}_{\mathrm{W}}=\frac{1}{n} \sum_{i=1}^m \sum_{l=1}^{N_i}\left(\boldsymbol{A}_l^i-\boldsymbol{\mu}_i\right)\left(\boldsymbol{A}_l^i-\boldsymbol{\mu}_i\right)^{\mathrm{T}}。\end{array}\right. $ | (11) |
Step 3:需保证SB尽可能小的同时SW尽可能大,以求得获得较好的特征分类效果。因此构造如下特征判据J,使得J越大,分类效果越好。
| $ J=\operatorname{tr}\left(\boldsymbol{S}_{\mathrm{W}}^{-1} \boldsymbol{S}_{\mathrm{B}}\right), $ | (12) |
对按C35×7M种取法得到的每一种M维特征样本集,根据式(12)计算一次J的大小,当J(ηk)为J的最大值时,认定ηk为最优M维特征。
文中采用基于RBF核的朴素贝叶斯分类模型进行训练及测试故障数据集并确定最优故障特征维数,该分类模型在下一节说明。具体过程如下:
Step 1:令初始M=2。
Step 2:按照上述方法选择最优M维特征。
Step 3:将最优M维特征组成训练集和测试集,用基于核分布的贝叶斯分类训练模型,获得测试分类准确率。
若AM<95%,则令M=M+1,返回步骤2。其中AM为最优M维特征样本集训练出的分类准确率;
若AM-AM-1≥1%,则令M=M+1,返回步骤2。
确定最优特征维数为M-1维,其分类模型和分类准确率为最终故障定位结果。
在确定最优故障特征维数时,需同时兼顾到分类模型的准确率和分类效率。经过大量实验验证,文中将分类准确率门槛定为95%,即当该维数的故障数据集训练和测试的区段定位结果准确率低于95%时,通过增加特征维数提高特征数据的代表性,从而提高最终分类准确率;当该维数的数据集训练出的分类准确率已达到95%及以上时,若进一步增加特征维数时分类准确率没有明显改善,则确定其为最优故障特征维数。笔者将分类准确率提高不足1%定为分类效率没有明显改善。考虑到一维特征数据分类结果不够理想,故选择从二维开始挑选最优故障特征维数。
4 基于RBF核的朴素贝叶斯分类确定最优故障特征维数需要同时兼顾分类准确率和分类效率,而朴素贝叶斯分类器相较于SVM等其他常见分类器的一个优势在于只根据少量的训练数据便能估计出必要的参数。因其假设变量独立,只需估计各个变量的算法,而不需要确定整个协方差矩阵。基于此,文中选取朴素贝叶斯作为算法中的分类器。
抽象地说,概率模型分类器是一个条件概率模型。
| $ p\left(C_k \mid x_1, \cdots, x_n\right)。$ | (13) |
独立变量Ck有k种类别,条件依赖于特征向量x=(x1, …, xn)。当特征数量n较大或者每个特征能取到大量值时,基于概率模型列出概率表变得不现实,需修改此模型使之变得可行。贝叶斯定理为
| $ p\left(C_k \mid x\right)=\frac{p\left(C_k\right) p\left(x \mid C_k\right)}{p(x)}。$ | (14) |
在实际情况中,由于分母不依赖于C而且特征xi的值是给定的,即分母可认为是常数。于是分子等价于联合分布模型为
| $ p\left(C_k, x_1, \cdots, x_n\right)。$ | (15) |
重复使用链式法则,将式(15)写成条件概率的形式,为
| $ \begin{aligned} & p\left(C_k, x_1, \cdots, x_n\right) \\ & \propto p\left(C_k\right) p\left(x_1, \cdots, x_n \mid C_k, x_1\right) \\ & \propto p\left(C_k\right) p\left(x_1 \mid C_k\right) p\left(x_2, \cdots, x_n \mid C_k, x_1\right) \\ & \propto p\left(C_k\right) p\left(x_1 \mid C_k\right) p\left(x_2 \mid C_k, x_1\right) \cdots p\left(x_n \mid C_k, x_1, x_2, x_3, \cdots, x_{n-1}\right)。\end{aligned} $ | (16) |
而“朴素”指每个特征Fi对于其他特征Fj(j≠i)是条件独立的,也就意味着:
| $ p\left(x_i \mid C_k, x_{i+1}, \cdots, x_n\right)=p\left(x_i \mid C_k\right)。$ | (17) |
因此,联合分布模型可表达为:
| $ \begin{aligned} & p\left(C_k \mid x_1, \cdots, x_n\right) \propto p\left(C_k, x_1, \cdots, x_n\right) \\ & \propto p\left(C_k\right) p\left(x_1 \mid C_k\right) p\left(x_2 \mid C_k\right) p\left(x_3 \mid C_k\right) \cdots \\ & \propto p\left(C_k\right) \prod\limits_{i=1}^n p\left(x_i \mid C_k\right), \end{aligned} $ | (18) |
这意味着在上述假设下,类变量C的条件分布可表达为:
| $ p\left(C_k \mid x_1, \cdots, x_n\right)=\frac{1}{Z} p\left(C_k\right) \prod\limits_{i=1}^n p\left(x_i \mid C_k\right), $ | (19) |
式中, 证据因子
| $ \operatorname{classify}\left(f_1, \cdots, f_n\right)=\underset{c}{\operatorname{argmaxp}}(C=c) \prod\limits_{i=1}^n p\left(F_i=f_i \mid C=c\right)。$ | (20) |
在实践中,经常会有连续的变量。对于连续变量,需要在x的所有观测值中实现x的概率。为了确定这些概率,提出了密度函数(density function)。为了获得期望的结果,要确保合适的分布近似值。由于属性数量激增,遍历手头的所有分布非常耗时。如果错误的假设与现实相去太远,那么预先指定形状可能会使后验的预测产生偏差。
核密度估计(kernel density estimation, KDE)首先对围绕每个观测值xr的密度相等地加权。这里需要用到核函数K——例如正态分布、三角形分布、epanechnikov分布或均匀分布。总结所有密度以获得密度函数。
| $ K_{\mathrm{KDE}}(x)=\frac{1}{h m} \sum_{r=1}^m K\left(\left(x-x_r\right) / h\right), $ | (21) |
式中:xr为分布均值;h为标准偏差,也称带宽。m个观测值的每个分布K((x-xr)/h)均以1/m加权。文中选用RBF核函数,它可以使有限维数据映射到高维空间以简化计算。
5 仿真分析文中在Matlab环境中基于图 2的IEEE 33节点10 kV配电网模型,仿真历史正常运行状态和故障状态,提取其行波小波数据进行训练和测试。为了实验测试对学习器的泛化误差进行较好评估,在机器学习的小数据样本中,训练集数据的数量应占2/3到4/5[17],故文中选用7:3的比例随机生成训练集和测试集。在实际计算中,文中测试了几种经典机器学习分类器在二维和三维条件下特征数据分类效果,如表 2所示。
| 表 2 与经典机器学习分类器相比基于RBF核的朴素贝叶斯对本模型特征数据分析效果 Table 2 Results of naive Bayes based on RBF kernel in analyzing the feature data of this model compared with the classical machine learning classifier |
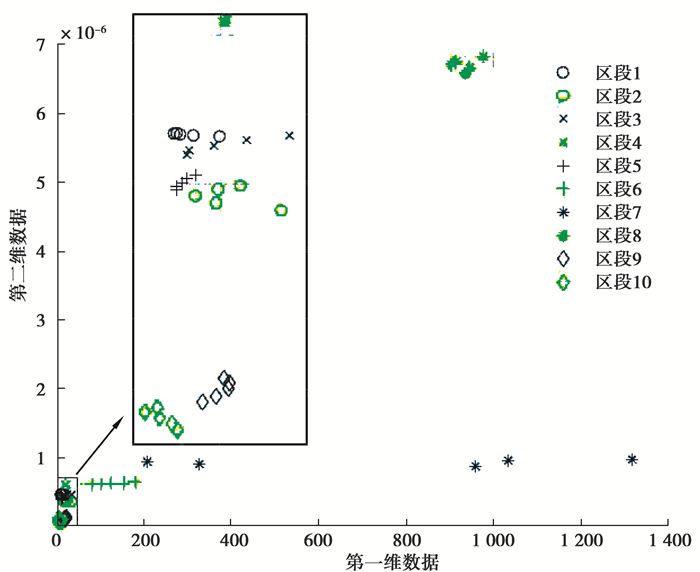
由表 2可看出,朴素贝叶斯系和SVM系对该特征数据集的分类效果相对较好,其中在三维特征维数下的基于核分布的贝叶斯和中高斯SVM分类准确率均达到了97.9%。考虑到贝叶斯分类相较于SVM有较快的训练速度,故文中采用的朴素贝叶斯分类更胜一筹。根据第4节的算法,从原始特征矩阵A中取出任意2个元素共有C35×62种取法,计算每一种取法的J值,容易得到二维最优特征为节点27的d2层小波能量和节点31的a6层小波能量。具体样本数据如图 4分布,其中不同颜色形状的数据点表示不同区段线路故障的测量数据,x轴和y轴分别为第一、第二维小波频带所带的能量特征。
|
图 4 IEEE 33节点模型最优二维故障特征分布 Fig. 4 Optimal 2-D fault feature of IEEE 33-bus model |
从图 4可以看出,不同线路区段故障时,样本数据点集中于不同的区域,说明该二维特征能较好地实现故障区段区分。将该二位特征样本输入至基于核分布的贝叶斯分类模型,得到故障区域定位准确率为90.3%。由于故障准确率未达到95%,需进一步增加特征维数以实现更优的分类效果。
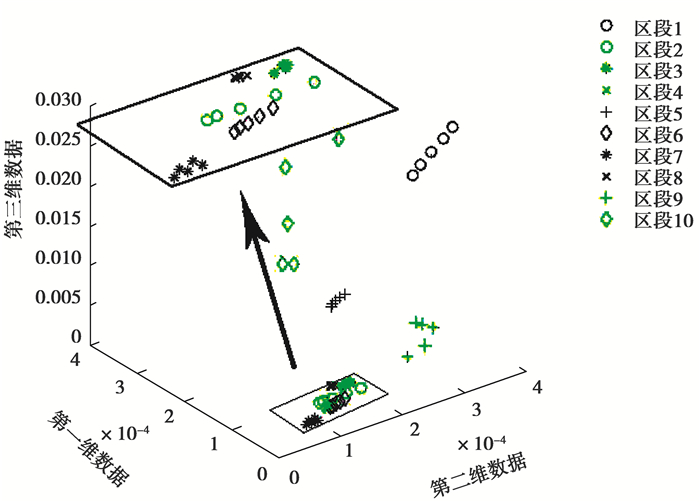
根据第4节中的方法,从原始特征矩阵A中取出任意3个元素共有C35×63种取法,计算每一种取法的J值,容易得到三维最优特征为节点2的d4层小波能量、节点19的d3层小波能量和节点22的a6层小波能量。具体样本数据如图 5分布,其中不同颜色的数据点表示不同区段故障的测量数据,x轴、y轴和z轴分别为第一、第二、第三维小波频带所带的能量特征。
|
图 5 IEEE 33节点模型最优三维故障特征分布 Fig. 5 Optimal 3-D fault feature of IEEE 33-bus model |
从图 5可以看出,不同线路区段故障时,样本数据点集中于不同的区域,说明该三维特征能较好地实现故障区段区分。将该三维特征样本输入至基于核分布的贝叶斯分类模型,得到故障区域定位准确率为97.9%。文献[11]以各频率分量电压幅值作为分类依据,文中最优三维特征定位准确率比它高2.9%,具有更好的区分度和可靠性。
因最优四维特征样本准确率相较于三维特征样本分类准确率并未提高1%以上,故考虑到分类效率及经济性原则,确定最优特征样本为三维特征样本,即选定由节点2的d4层小波能量、节点19的d3层小波能量和节点22的a6层小波能量组成的最优三维特征样本能准确实现配电网故障定位。
在实际应用中,由于在节点站域附近故障时可能会定位到相邻线路,因此可将分类结果中的故障区段再向先后各延伸一个区段,由这几个线路共同组成疑似故障区段。在本实验中,加入疑似故障区段后的最优三维特征定位准确率为98.3%,达到了提高该方法容错性的目的。但该方法牺牲了部分定位精确度,如何有效解决这一弊端还有待未来进一步探讨。
6 结论随着DG大量接入配电网,许多传统配电网故障定位方法已不再适用。笔者依据行波小波特征值数据,运用集成思想结合LDA与基于核分布的贝叶斯分类的有源配电网故障定位技术,在带故障运行的状态下,仅通过分析3个测点的行波数据,就能快速准确地确定单相接地故障的故障区段,故障分析特征数据量较少,仅需3个节点小波数据,且可靠性高,定位准确率达到了97%以上。
| [1] |
薛永端, 李娟, 徐丙垠. 中性点经消弧线圈接地系统小电流接地故障暂态等值电路及暂态分析[J]. 中国电机工程学报, 2015, 35(22): 5703-5714. Xue Y R, Li J, Xu B Y. Transient equivalent circuit and transient analysis of single-phase earth fault in arc suppression coil grounded system[J]. Proceedings of the CSEE, 2015, 35(22): 5703-5714. (in Chinese) |
| [2] |
Wang X W, Zhang H X, Shi F, et al. Location of single phase to ground faults in distribution networks based on synchronous transients energy analysis[J]. IEEE Transactions on Smart Grid, 2020, 11(1): 774-785. DOI:10.1109/TSG.2019.2938667 |
| [3] |
陈奎, 张云, 王洪寅, 等. 基于免疫算法的含分布式电源配电网的故障定位[J]. 电力系统保护与控制, 2017, 45(24): 57-62. Chen K, Zhang Y, Wang H Y, et al. Fault-section location of distribution network containing distributed generation based on immune algorithm[J]. Power System Protection and Control, 2017, 45(24): 57-62. (in Chinese) DOI:10.7667/PSPC161971 |
| [4] |
廖志伟, 叶青华, 王钢, 等. 基于GRNN的多故障自适应电力系统故障诊断[J]. 华南理工大学学报(自然科学版), 2005(9): 6-9. Liao Z W, Ye Q H, Wang G, et al. Adaptive multi-fault diagnosis of power system based on GRNN[J]. Journal of South China University of Technology(Natural Science Edition), 2005(9): 6-9. (in Chinese) |
| [5] |
Guo M F, Gao J H, Shao X, et al. Location of single-line-to-ground fault using 1-D convolutional neural network and waveform concatenation in resonant grounding distribution systems[J]. IEEE Transactions on Instrumentation and Measurement, 2021(70): 1-9. |
| [6] |
Xie L W, Luo L F, Li Y, et al. A traveling wave-based fault location method employing vmd-teo for distribution network[J]. IEEE Transactions on Power Delivery, 2020, 35(4): 1987-1998. DOI:10.1109/TPWRD.2019.2959188 |
| [7] |
Shi S X, Zhu B E, Lei A Y, et al. Fault location for radial distribution network VIA topology and reclosure-generating traveling waves[J]. IEEE Transactions on Smart Grid, 2019, 10(6): 6404-6413. DOI:10.1109/TSG.2019.2904210 |
| [8] |
Bahmanyar A, Jamali S. Fault location in active distribution networks using non-synchronized measurements[J]. International Journal of Electrical Power & Energy Systems, 2017(93): 451-458. |
| [9] |
Zhang T, Li X H, Yu H B, et al. A fault location method for active distribution network with renewable sources based on bp neural network[C]//2015 7th International Conference on Intelligent Human-Machine Systems and Cybernetics. Hangzhou, China, 2015: 357-361.
|
| [10] |
梁睿, 崔连华, 都志立, 等. 基于广域行波初始波头时差关系矩阵的配电网故障选线及测距[J]. 高电压技术, 2014, 40(11): 3411-3417. Liang R, Cui L H, Du Z L, et al. Fault line selection and location in distribution power network based on traveling wave time difference of arrival relationships[J]. High Voltage Engineering, 2014, 40(11): 3411-3417. (in Chinese) |
| [11] |
刘科研, 董伟杰, 肖仕武, 等. 基于电压数据SVM分类的有源配电网故障判别及定位[J]. 电网技术, 2021, 45(6): 2369-2379. Liu K Y, Dong W J, Xiao S W, et al. Fault identification and location of active distribution network based on SVM classification of voltage data. power system technology[J]. Power System Technology, 2021, 45(6): 2369-2379. (in Chinese) |
| [12] |
Pourahmadi-Nakhli M, Safavi A A. Path characteristic frequency-based fault locating in radial distribution systems using wavelets and neural networks[J]. IEEE Transactions on Power Delivery, 2011, 26(2): 772-781. |
| [13] |
Qiao J, Yin X G, Liu X Y, et al. An accurate fault-location method for distribution network with distributed generators based on multi-terminal traveling wave[C]//2020 IEEE Sustainable Power and Energy Conference (iSPEC), 2020: 1867-1873.
|
| [14] |
贾科, 董雄鹰, 李论, 等. 基于稀疏电压幅值量测的配电网故障测距[J]. 电网技术, 2020, 44(3): 835-845. Jia K, Dong X Y, Li L, et al. Fault location for distribution network based on transient sparse voltage amplitude measurement[J]. Power System Technology, 2020, 44(3): 835-845. (in Chinese) |
| [15] |
梁睿, 靳征, 王崇林, 等. 行波时频复合分析的配电网故障定位研究[J]. 中国电机工程学报, 2013, 33(28): 130-136. Liang R, Jin Z, Wang C L, et al. Research of fault location in distribution networks based on integration of travelling wave time and frequency analysis[J]. Proceedings of the CSEE, 2013, 33(28): 130-136. (in Chinese) |
| [16] |
Akbar M A, Ali A A S, Amira A, et al. An empirical study for PCA- and LDA-based feature reduction for gas identification[J]. IEEE Sensors Journal, 2016, 16(14): 5734-5746. |
| [17] |
Nguyen Q H, Ly H B, Ho L S, et al. Influence of data splitting on performance of machine learning models in prediction of shear strength of soil[J]. Mathematical Problems in Engineering, 2021, 2021: 4832864. |
 2022, Vol. 45
2022, Vol. 45

