传统的经典结构力学在教学内容与方法上大同小异,教学活动封闭,缺乏活力,学生独立思考的空间有限,对人才培养较为不利。随着结构设计和分析软件(如PKPM、3D3S、SAP2000和ABAQUS等)在科研单位和设计单位的普遍采用,软件使用者从繁琐的计算中解脱,但这并未使学生的能力素养得到全面提升。反而,对软件过于依赖,学生独立思考的空间愈加狭窄,对力学的基本概念与理论变得更加模糊。基于此,为培养具备扎实力学理论知识的创新型人才,应在结构力学授课过程中努力提高学生的概念分析能力,使学生深入理解与运用结构力学的核心概念和基本方法来解决实际工程问题。结构概念是对建筑结构的一般规律和最本质特征的认识,正确的结构概念有助于深刻理解结构的受力特性,从而更合理地进行结构设计[1, 2]。
近些年,概念结构力学(又称定性结构力学、感知结构力学或结构的哲学)得到了高校科教人员的普遍重视,多位专家教授[3, 4, 5]积极呼吁在经典结构力学授课过程中培养学生的结构概念分析能力,使学生掌握结构概念分析的一般方法与规律,让学生学会用全方位、多角度的眼光去认识与分析力学问题。概念结构力学面向素质与能力的培养目标正与教育部开展的质量工程建设内容不谋而合[6]。
桁架结构(TrussStructure)是结构力学课程主要研究的结构形式之一,在各 类工程结构中应用甚广,如屋盖结构、桥梁工程和水工闸门等。按力学简图常分为简支桁架与连续桁架、静定桁架与超静定桁架、平面桁架与空间桁架,按外形分为平行弦、梯形、三角形与多边形桁架,按杆件内力与截面、节点构造特点分为普通、重型与轻型桁架,按所用材料分为钢桁架、钢筋混凝土桁架、木桁架、铝合金桁架及组合桁架。提高桁架结构的概念分析能力,对设计方案的优选、结构的合理选型、力流传递的理解、结果的正误判断具有重要的指导意义。
二、桁架结构概念分析的内容 (一) 受弯构件形式的演变工业与民用建筑采用的矩形截面梁是最为常见的受弯构件,但其材料利用率低,因应力沿截面高度方向分布极不均匀,且弯矩沿梁长通常是变化的。于是,人们通过“掏空”矩形截面梁的腹部得到了工字型梁、箱型截面梁等,从而大大减轻了结构的自重,使材料利用率得到提升。为了更大限度地提升材料利用率,将工字梁的腹板继续“掏空”,得到了目前工程中应用广泛的蜂窝梁。矩形截面梁另一种“掏空”的结构形式就是桁架。桁架可理解为“掏空”的梁,简支桁架上弦受压,下弦受拉,二者承担对应截面的弯矩,腹杆有拉有压,承担对应截面的剪力。为进一步构造更为合理的结构形式,可将桁架外形设计成与弯矩图相类似的形状,如折弦形桁架,可使桁架的弦杆受力更为均匀、合理。实腹拱结构的截面主要受压,弯矩和剪力均很小,材料利用率高,但实腹拱结构施工难度大,构造复杂,于是桁架拱结构便应运而生。从普通梁到桁架的发展过程,体现了人们对合理结构形式的追求与向往,也体现了概念设计对提高材料效用、探索新型结构形式的指导意义[7]。
(二) 桁架杆件的受力状态结构力学的经典解题方法不仅可用于定量计算,也是概念分析的重要手段。在授课过程中可将定量计算与概念分析相结合,来加深学生对解题方法的理解,促使学生形成概念分析的思维。
例如:在计算桁架杆件内力时,若不求解杆件的内力值,是否能快速判断图 1所示桁架指定杆件的拉压状态。该问题可采用已学过的截面法作定性判断[8]。
|
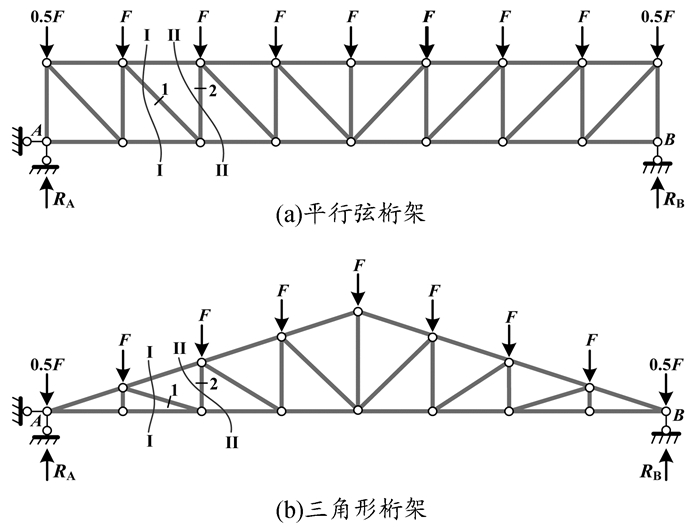
图1 桁架 |
图 1a中的平行弦桁架,作截面I-I,取左半部为隔离体,列∑FY=0,显然支座反力RA大于隔离体上的荷载,所以杆1轴力方向向下,即斜杆1受拉;同理,作截面II-II,可快速判断竖杆2受压。进一步,可快速判断竖杆、斜杆的轴力大小均分别由两端向中间递减。为何有此现象,可将该桁架想象成简支梁,则剪力端部最大,跨中最小,从端部向跨中剪力逐渐减小,而剪力是由腹杆(竖杆、斜杆)承担,因此腹杆的轴力从端部向跨中递减。对于图 1b中的三角形桁架,作截面I-I、II-II,列∑MA=0,也能快速判断出杆件的拉压状态,并可判断其竖杆与斜杆的轴力大小均由两端向中间递增,这一趋势与平行弦桁架正好相反。
弯矩图、剪力图有时有助于区分桁架杆的拉压状态。通常,对于平行弦桁架,如图 2a所示,当受正弯矩时,上弦杆受压,下弦杆受拉,类似于梁上下两侧的纤维。当受负弯矩时,恰好相反。当受正剪力时,向右下倾的杆件受拉,向右上倾的杆件受压,如图 2b所示,图 2b表示腹杆轴力竖向分量所承受的剪力。当受负剪力时,正好相反。当剪力为零时,弦杆、腹杆内力均为零。

|
图2 平行弦桁架 |
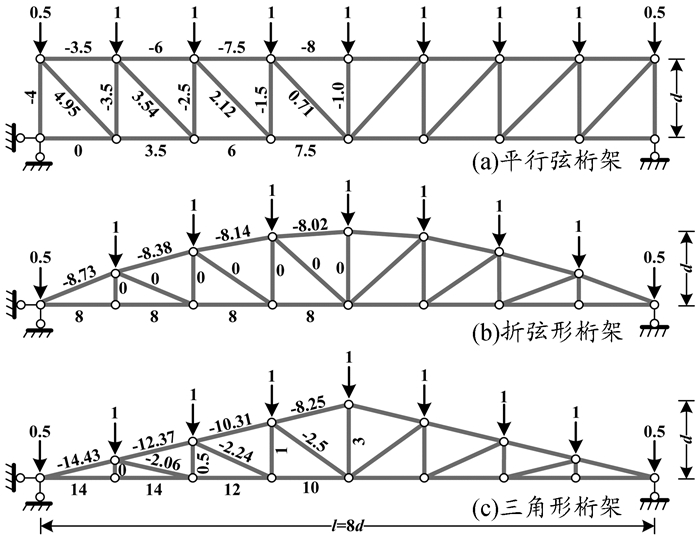
不同外形的桁架具有不同的受力特性[9],如图 3所示,在设计时应予以考虑。平行弦桁架的竖杆、斜杆轴力的竖向分量等于简支梁相应位置上的剪力,故由跨中向两端递增,如图 3a所示。折线形桁架上弦呈拱形,均布荷载作用下,该类桁架外形与简支梁弯矩图形相似,所以上下弦杆轴力分布均匀,腹杆轴力小,用料省,是工程中常用的一种桁架形式。若上弦节点均位于二次抛物线上,上弦符合合理拱轴线,全部腹杆内力为零,下弦杆轴力相等,如图 3b所示,该桁架可看作静定拉杆拱,上弦即为拱肋,下弦为拉杆。三角形桁架在沿跨度均布节点荷载作用下,上下弦杆的轴力在端部最大,向跨中逐渐减少,腹杆(竖杆、斜杆)的轴力变化趋势正好相反,如图 3c所示。三角形桁架因弦杆内力差别较大,材料消耗不合理,多用于瓦屋面的屋架中。
|
图3 不同外形的桁架 |
选择桁架形式时,应综合考虑桁架的功能、材料、约束条件与施工条件等,选型的原则是在满足功能要求的前提下,力求制造、安装所耗用的材料和劳动量为最小。例如,坡度较陡的屋架通常采用三角形桁架,较平缓的屋架通常采用梯形桁架,其他类型桁架通常采用构造较简单的平行弦桁架,因为平行弦桁架杆件长度统一,制造、施工方便。折弦形桁架受力良好,但杆件长短不一,施工复杂,因此在大跨度桁架中较多采用。钢筋混凝土和预应力混凝土桁架则多为多边形、梯形。
(四) 桁架刚度的概念分析桁架的整体刚度是以控制其最大竖向挠度不超过容许挠度来保证的。平面桁架的面外刚度较弱,须布置侧向支撑体系,如檩条等。
在计算桁架杆件的强度、稳定时,内力按轴心受力构件进行考虑。当杆件同时承受轴力、弯矩作用时,按拉弯或压弯构件来考虑。桁架结构中存在的受压杆件往往由其稳定性控制,尤其是长细比较大的杆件,而并不是由截面材料强度来控制。所以应尽量降低受压杆的长细比。在计算杆件的稳定性、长细比时,须考虑面内、面外两个方向,或者长细比较大的方向。
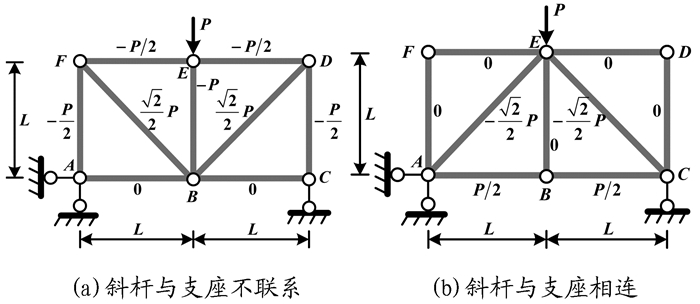
桁架设计时应注重多个杆件的受力均衡问题,对静定桁架尤其如此。判断桁架是否受力均衡,整体刚度是一个重要指标。垂直荷载作用下桁架的整体刚度通常采用跨中挠度来衡量,挠度越大,刚度越小;挠度越小,则刚度越大。图 4a和图 4b所示两种桁架跨度相同、高度相同、杆件截面相同、材料相同、荷载相同,仅斜杆组成形式不同,在此比较二者的整体竖向刚度[10]。
|
图4 桁架构成与变形关系 |
一个外荷载作用在上弦,求B结点竖向变形。外载作用下各杆轴力如图 4所示,拉为正,压为负。单位荷载竖直向下作用于B结点。根据“单位荷载法”计算桁架B节点竖向位移
| $ \Delta B,a = \frac{{PL}}{{EA}}\left( {2 + \sqrt 2 } \right) $ | (1) |
| $ \Delta B,b = \frac{{PL}}{{EA}}\left( {0.5 + \sqrt 2 } \right) $ | (2) |
比较式(1)、式(2)可发现,因斜杆布置方式的不同导致了结构竖向刚度不同,图 4b的斜杆直接将荷载传递给支座A和C,其竖向刚度提高了许多。显然,从竖向刚度的角度来看,“斜杆直接连接支座”的方式较好。说明荷载直接传入支座的重要性。
以上从刚度角度来看,图 4b所示桁架明显优于图 4a所示桁架。但从受力性质看,在图示荷载作用下,图 4a为“长杆(斜杆)受拉”,而图 4b为“长杆(斜杆)受压”,受压杆就需考虑“失稳”问题。从受力角度来看,图 4a桁架更有利。所以,设计时采用哪种形式的桁架,既要考虑设计目标,又要考虑荷载情况。
(五) 计算机技术与桁架结构概念分析数值模拟方法的快速发展拓宽了结构力学的应用范畴,学生可借助有限元软件(如ANSYS、ADINA和ABAQUS等)分析更为复杂的桁架结构,ANSYS软件提供的APDL(ANSYS Parametric Design Language),使桁架结构的参数化建模、加载、计算更为便捷。目前,在结构力学教学总学时数逐渐减少的情况下,需要在有限的教学课时内将有限元计算与概念分析的内容高效地引入课程教学。笔者在桁架计算的教学中引入了ANSYS仿真实验内容,激发了学生的学习兴趣,拓展了学生的知识层面,使学生概念分析能力得到了提高。同时,软件的使用造成“重计算,轻分析”的现象。龙驭球院士曾指出:“在大型计算中,如果不会概念判断,不会抓错、改错,那是很危险的。”因此,在结构力学的授课过程中,应注重培养学生的概念分析能力,使学生认识到有限元软件是进行桁架结构概念分析的工具,而概念分析则是有限元计算中不可缺少的环节。
(六) 对桁架工程实例的概念分析因结构力学的概念较抽象,若不结合实际工程问题,学生在学习过程中会感到晦涩难懂。若能在结构力学课程教学中加入桁架工程实例,并与结构概念分析相结合,则可使学生既掌握桁架结构的基本知识,又能了解桁架结构最新研究进展。如适当将拱桁架、张弦桁架的平面内稳定和平面外稳定等知识点引入教学,既能培养学生的基本素养,又能强化学生的工程概念。对桁架工程实例的概念分析,不仅能加强学生对桁架基本理论知识的理解,还能使学生学会运用新思想与新技术来研究、解决实际工程问题。
三、结语桁架结构作为工程中普遍采用的一种结构形式,其概念分析与设计贯穿于整个结构设计当中。概念分析与设计是人类的思维活动,在工程结构力学计算的基础之上,努力探索新型构件与结构形式,提高设计水平,充分发挥材料的效用,使其受力尽量合理、安全、适用与美观。
综上所述,结构力学的教学活动应当以培养高素质的创新型人才为目标,既要让学生理解和掌握力学规律与理论基础知识,更要提高学生的概念分析能力,引导学生逐步增强概念分析意识。
| [1] | 林同炎,S D 思多台斯伯利. 结构概念和体系 [M]. 北京:中国建筑工业出版社,1985.( 1) 1) |
| [2] | Torroja Eduardo. Philosophy of Structures [M]. University of California Press, 1958.( 1) 1) |
| [3] | 龙驭球. 学习方法论 [J]. 中国大学教学,1999(6):12-14.( 1) 1) |
| [4] | 袁驷. 一个基础,两座大厦——结构力学课程的改革思路与实践 [J]. 力学与实践,1998,20(4):56-58.( 1) 1) |
| [5] | 朱慈勉,尹小明. 概念设计的意义和应用分析 [J]. 建筑技术,2008,36(8):626-628.( 1) 1) |
| [6] | 周臻,陆金钰,尹凌峰,等. 面向卓越土木工程师培养的结构力学教学改革与实践[J]. 高等建筑教育,2012,21(4):74-77.( 1) 1) |
| [7] | 刘永军,宋岩升,王宇. 结构力学课程"四模块体系"探索及实践 [J]. 黑龙江教育:高教研究与评估,2012(3):4-5.( 1) 1) |
| [8] | 许凯,陈朝峰,杨祖权. 定性分析在结构力学教学中的应用研究 [J]. 高等建筑教育,2010, 19(6):98-101.( 1) 1) |
| [9] | 朱慈勉. 结构力学[M]. 2版.北京:高等教育出版社,2009.( 1) 1) |
| [10] | 黄达海. 概念结构力学 [M]. 北京:北京航空航天大学出版社,2010.( 1) 1) |
 2016, Vol. 25
2016, Vol. 25

