b. 西安建筑科技大学 图书馆, 陕西 西安 710055
b. Library, Xi'an University of Architecture and Technology, Xi'an 710055, P. R. China
动态模拟技术借助计算机强大的计算和图像处理能力,可以高效地进行复杂计算,同时能将计算过程和结果以图形的方式呈现给用户,实现了抽象问题具体化、图像化,是解决复杂科学和工程问题的有效工具,在科研和工程领域得到了越来越广泛的应用。建筑能耗模拟技术在建筑节能设计、绿色建筑评价、生态建筑设计等领域被大量使用[1-2]。在建筑物理教学中,应加强计算机科学和数字技术在物理环境设计和计算中的应用[3]。模拟技术被越来越多的学科所重视,如何提高模拟课程教学效果,是很多学科在模拟课程教学方面都面临的迫切问题。
建筑能耗模拟课程是西安建筑科技大学建筑学院为建筑技术科学专业硕士研究生开设的专业选修课。其教学目标就是培养学生依据建筑能耗计算原理,使用模拟计算软件,独立开展模拟计算分析。特别是硕士研究生的模拟课,不仅培养学生操作软件的动手能力,而且培养学生独立设计模拟方案、客观准确分析模拟结果等综合性能力。目前,建筑能耗模拟的教学中采用的教材以及研究论文,不是讲述能耗计算的普适性原理和公式[4],就是介绍软件操作方法、案例分析[5]。在一些研究生的能耗模拟研究中,也主要是以原理、机理、方法宏观层面的内容为主,对其软件的核心算法、运行机制研究很少[6-7]。
针对该课程的这一特征,传统的传输式教学方式在长期的教学活动中暴露出对学生综合实践能力培养严重不足的问题。因此,需采用新的教学方式以弥补、改善在模拟综合能力培养中存在的尖锐问题。
二、体验式教学方式在建筑能耗模拟教学中的可行性分析教学方式是影响教学效果的重要环节,针对不同性质的课程应采用不同的教学方式。体验式教学方式能为具有实践性、应用性课程的教学带来深刻的变革,强化培养学生的实际操作能力,以及在实践工作中分析问题与解决问题的能力。
体验式教学最早由美国凯斯西储大学组织行为学教授David Kolb在20世纪70年代提出,其核心思想是“学习是经验转化为知识的过程,知识源于掌握经验和转化经验的结合体”[8]。体验式教学的本质特征是符合“螺旋上升、不断深入”的学习规律[9],强调的是以学习者为中心的自主学习,而传统教学强调的是教师为中心的知识传递,反对传统教学以教师为中心、课堂为中心、教材为中心,主张教学应以学生为中心、活动为中心、经验为中心[10]。凡是以活动开始的,先行后知的,都可作为“体验式教学”。与传统教学相比,体验式教学不是简单的教学方式改变,而是将认识过程与情意过程融合与统一。体验式教学方式是基于对经验的重视和强化,是以学生为中心的教学组织方式,能满足对学生动手能力、分析能力以及综合能力的培养需求,这些正是建筑能耗模拟课程的培养目标。
模拟课程的教学内容主要包括两部分:模拟的计算理论和模拟软件的使用。现存主要问题是,主流的模拟软件大部分由国外软件厂商编制,即使有国内成熟的软件,其软件运行机制和流程都是黑箱,因此教学中很难把模拟理论和软件的使用相对应,造成模拟理论与软件操作的严重脱节。课程讲授中,如果偏重理论,会造成学生对软件操作能力的不足,而偏重软件使用,则会造成模拟方案设计欠缺,及对软件模拟结果分析不足。因此,亟需为学生创建模拟理论到操作软件的桥梁,让学生深入理解模拟的本质内涵是计算分析,而不是简单的软件操作。
体验式教学方式的核心是发挥学生能动性,通过学生参与的教学活动,以体验方式强化能耗模拟知识的经验增长,以亲自参与的方式搭建理论和操作之间的桥梁。学生的具体参与方式为:选取较为简单的模拟理论,通过自己手动演算或者编程的方式,来完成一个特定问题的模拟分析。建筑技术科学是一门特殊的学科,没有本科专业,其硕士研究生的本科专业背景众多,包括暖通、土木甚至计算机应用专业,因此,应充分利用学生的本科专业背景,发挥其特长。教学中,对学生按照不同专业背景进行分组,保证每组既有建筑相关专业学生,又有软件素养高的相关专业学生。以小组为单位,有人负责理论学习,有人负责计算或编程。
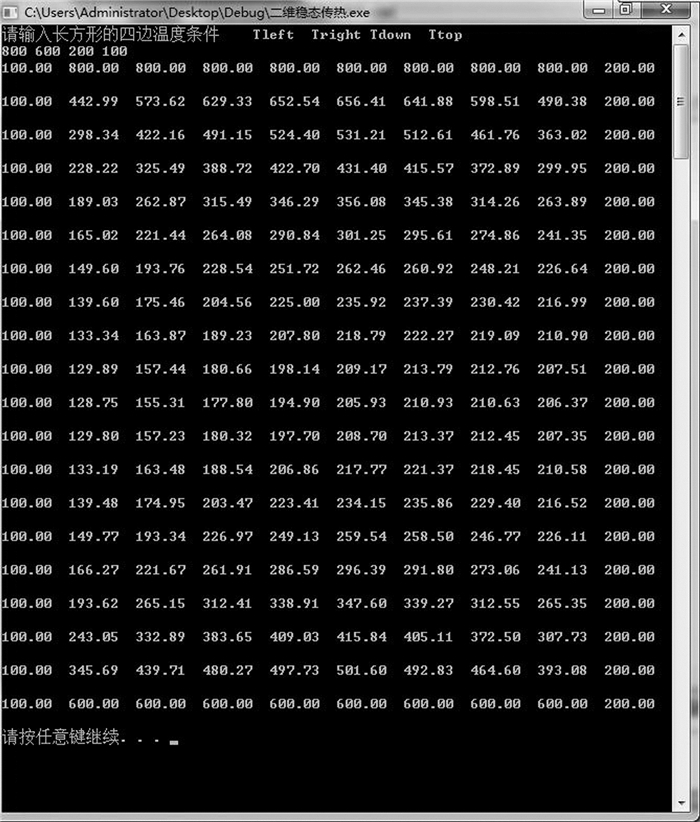
三、建筑能耗模拟课程引入体验式教学的案例分析建筑能耗模拟被安排在研一第二学期,学生已学习了建筑能耗计算的相关理论,为进行理论演算奠定了基础。在2015—2016学年第二学期的建筑能耗模拟课程上开展此次教学改革,将18位学生分为2组,小组1选题为非稳态傅里叶传热计算模型,小组2选题为二维结构性热桥的线传热系数计算。每个小组分别由擅长理论计算和计算机编程的学生组成。经过5周的课堂和课后工作,2个小组都提交了计算分析报告和软件编制说明。2个小组编制的软件如图 1、图 2所示。小组1采用C++语言编制了带有交互界面的软件,其计算参数可以自由输入,小组2采用C语言编制了无界面的文本运行程序,其运行参数在程序中固定。
|
图 1 小组1的软件界面 |
|
图 2 小组2的运行结果 |
傅里叶传热计算模型是解决墙体导热传热计算问题的有效方法,采用该方法可在已知墙体两侧空气温度情况下,计算墙体两侧的壁面温度,为墙体传热计算以及热舒适分析等方面奠定坚实基础。但通常工程计算所采用的稳态方法忽略了气温和墙体温度的动态变化规律,因此必须采用非稳态方法来研究傅里叶的墙体导热计算模型。
根据建筑热工原理,墙体导热传热的傅立叶定理一维非稳态计算公式如式1所示。
| $ \frac{{\partial t\left( {x, \tau } \right)}}{{\partial \tau }} = a\frac{{{\partial ^2}t\left( {x, \tau } \right)}}{{\partial {x^2}}} $ | (1) |
式中:x——围护结构厚度,m;
τ——时间,s;
a——围护结构材料的导温系数,m2/h;
λ——材料的导热系数,W/m·K。
对上述墙体传热微分方程,采用有限差分法进行求解,将其墙体看作均质材料层,按照等厚度划分,从外表面开始分层,其差分形式如式2所示。
| $ \frac{{\lambda \Delta \tau }}{{c\rho \mathit{\Delta }{x^2}}}\left[ {t_k^{m - 1} - \left( {\frac{1}{{\frac{{\lambda \Delta \tau }}{{c\rho \Delta {x^2}}}}} + 2} \right)t_k^m + t_{k + 1}^m} \right] = - t_k^{m - 1} $ | (2) |
式中:λ——材料的导热系数,W/m·K;
c——材料的比热,kJ/kg·K;
ρ——材料的密度,kg / m3;
tkm——围护结构第k层m时刻的温度,℃。
使用第三边界条件,给出室内外空气温度。边界条件的数学表述如式3所示,其差分表达如式4所示。
| $ \lambda \frac{{\partial t}}{{\partial x}} = \alpha \left( {\theta - t} \right) $ | (3) |
| $ \frac{{2{\lambda _1}}}{{\mathit{\Delta }{x_1}}}t_1^m - \left( {\frac{{2{\lambda _1}}}{{\mathit{\Delta }{x_1}}} + {\alpha _e}} \right)t_0^m = - {\alpha _e}t_e^m $ | (4-1) |
| $ \frac{{2{\lambda _n}}}{{\mathit{\Delta }{x_n}}}t_n^m - \left( {\frac{{2{\lambda _n}}}{{\mathit{\Delta }{x_n}}} + {\alpha _r}} \right)t_{n + 1}^m = - {\alpha _r}t_r^m $ | (4-2) |
式中:tem, trm——室外环境温度,室内环境温度,℃;
αe, αr——外表面换热系数,内表面换热系数,W/m2·K。
根据公式2和4,构建围护结构导热差分方程组,使用追赶法求解围护结构的外表面温度,然后依据表面换热原理计算通过围护结构外表面的热流。
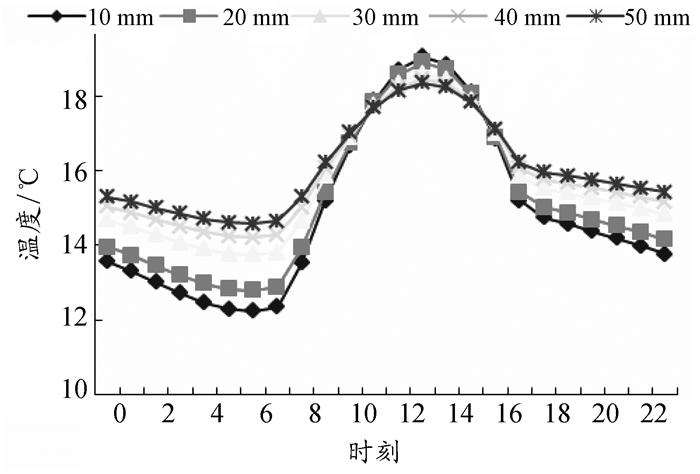
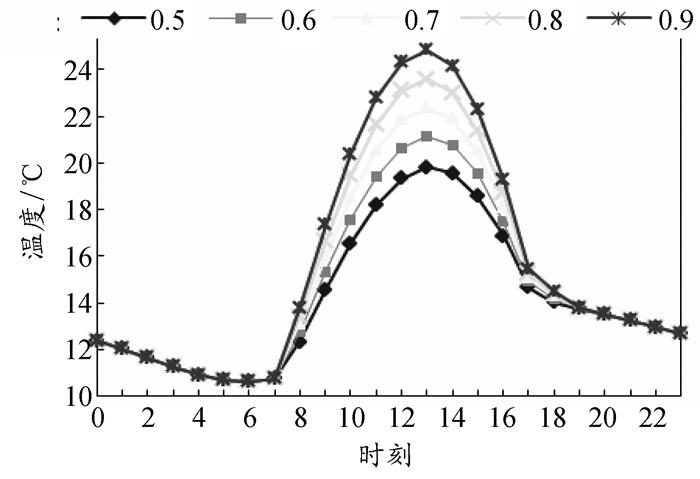
小组1根据此原理,采用C++语言,编制了读取参数的界面和傅里叶导热微分的求解过程,其计算结果为分层围护结构表面温度,以txt文件形式保存。图 3、图 4为采用该软件计算某地冬季不同构造形式外墙的内壁面温度变化规律。
|
图 3 不同保温层厚度内壁面温度 |
|
图 4 不同墙体厚度内壁面温度 |
目前绝大部分建筑能耗计算方法和软件都采用一维传热模型来计算围护结构耗热量,实际建筑围护结构中普遍存在的二维和三维传热现象通常被忽略或简化处理,这就使热桥对整个建筑的附加能耗影响误差越来越大。可以证明,随着保温层厚度的增加和建筑围护结构保温性能的提高,对热桥引起的建筑能耗增加量的计算己成为建筑节能技术的关键问题,因此,较为准确地给出热桥部位的定量评价指标意义重大。
国际标准ISO10211[11]中利用线传热系数ψ来描述结构性热桥对墙体、屋面传热的影响,可通过式5计算得到。
| $ \psi = \frac{{{Q^{2D}} - KA({t_n} - {t_e})}}{{l({t_n} - {t_e})}} = \frac{{{Q^{2D}}}}{{l({t_n} - {t_e})}} - KB $ | (5) |
式中:A——以热桥为一边的某一块矩形墙体的面积,m2;
l——热桥的长度,计算ψ时通常取lm;
B——该块矩形另一条边的长度即A=B·l,一般情况下B≥lm;
Q2D——通过该块墙体的热流,W;
K——墙体主断面的传热系数,W/(m2·K);
tn——墙体室内侧的空气温度,K;
te——墙体室外侧的空气温度,K。
式5中最关键的是求出通过该热桥部位围护结构的热流Q2D,对其通常采用二维稳态导热的傅里叶定理结合有限差分法数值传热方法进行计算。其计算原理同上例,这里不再赘述,其离散后的计算公式如式6所示。
| $ \frac{{{t_{i + 1, j}} - 2{t_{i, j}} + {t_{i - 1, j}}}}{{{{\left( {\mathit{\Delta }x} \right)}^2}}} + \frac{{{t_{i, j + 1}} - 2{t_{i, j}} + {t_{i, j - 1}}}}{{{{\left( {\mathit{\Delta }y} \right)}^2}}} = 0 $ | (6) |
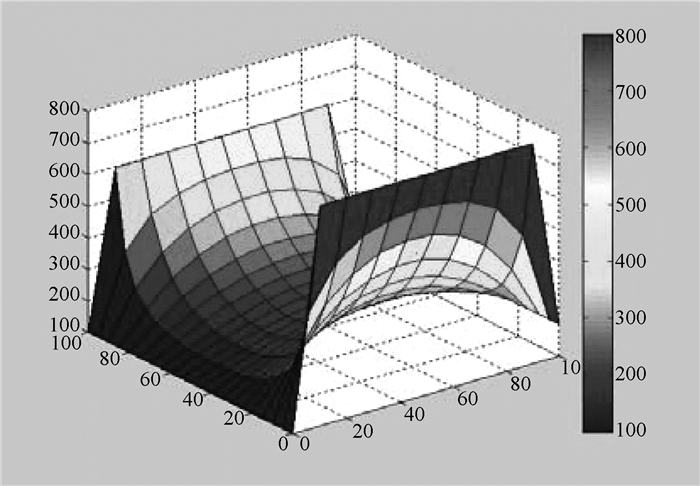
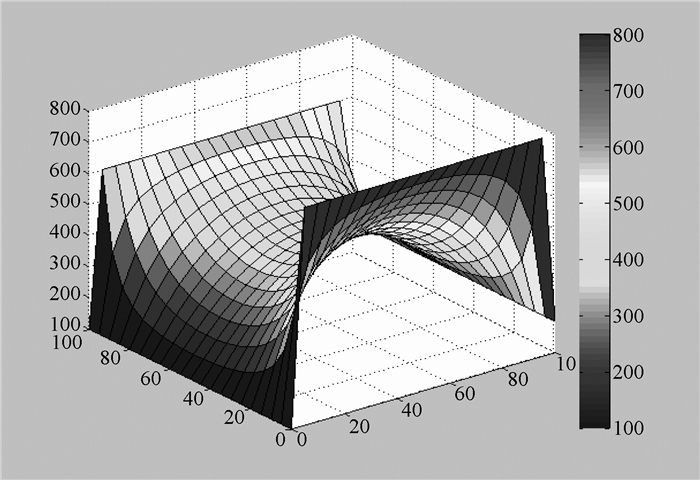
小组2将此计算过程用C语言程序化,利用该程序的计算结果,结合MATLAB编程,将其计算结果可视化,图 5为有限差分法求解中不同网格划分密度的温度分布图。在求解出热桥温度分布规律后,依据傅里叶定理可计算出通过热桥的热流。
|
图 5a 低密度网格构件温度分布 |
|
图 5b 高密度网格构件温度分布 |
建筑能耗模拟是一门实践性强,同时理论要求也较高的课程,常规填鸭式教学模式难以满足教学目标的需求,注重实践特征的体验式教学模式鼓励学生更多地参与教学活动,以其所具备的启发性、能动性、探索性卓有成效地激发了学生对该课程学习的主观能动性。在此次教学尝试中,学生通过参与理论方法梳理、手动演算、程序化设计和编程等环节的训练,系统地理解了模拟方法,深化了对模拟技术的认识,拨开了模拟软件神秘的面纱,提高了学生运用模拟方法分析问题的能力。
| [1] |
清华大学DeST开发组. 建筑环境系统模拟分析方法-DeST[M]. 北京: 中国建筑工业出版社, 2006.
|
| [2] |
MF Jentsch, ABS Bahaj, PAB James. Climate change future proofing of buildings -Generation and assessment of building simulation weather files[J]. Energy and Buildings, 2008, 40(12): 2148-2168. DOI:10.1016/j.enbuild.2008.06.005 |
| [3] |
陈仲林, 杨春宇, 何荥. 建筑物理实践教学法研究[J]. 南方建筑, 2008(5): 58-60. DOI:10.3969/j.issn.1000-0232.2008.05.014 |
| [4] |
王福军. 计算流体动力学分析——CFD软件原理与应用[M]. 北京: 清华大学出版社, 2004.
|
| [5] |
云朋. Ecotect建筑环境设计教程[M]. 北京: 中国建筑工业出版社, 2007.
|
| [6] |
李准.基于EnergyPlus的建筑能耗模拟软件设计开发与应用研究[D].长沙: 湖南大学, 2009. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1510029
|
| [7] |
首灵丽.基于BIM技术的建筑能耗模拟分析与传统建筑能耗分析对比研究[D].重庆: 重庆大学, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10611-1013044925.htm
|
| [8] |
Kolb D. Experiential Learning:Experience as the Source of Learning and Development[M]. Englewood Cliffs: Prentice Hall, 1984: 41.
|
| [9] |
郭佳, 李光霞. 从传输式教学到体验式教学[J]. 北京交通大学学报(社会科学版), 2010, 9(1): 124-128. DOI:10.3969/j.issn.1672-8106.2010.01.023 |
| [10] |
Smith T E, Roland C C, Havens M D. The theory and practice of challenge education[J]. Adventure Education, 1992, 293. |
| [11] |
ISO.ISO10211-2: 2001 Thermal bridges in building construction, calculation of heat flows and surface temperature, Part 2: Linear thermal bridges[S].2001.
|
 2018, Vol. 27
2018, Vol. 27

