径向滑动轴承广泛应用于各种旋转机械中,其摩擦学性能的好坏直接影响着整机的寿命。滑动轴承润滑的计算实际为相关控制方程的求解。1886年,在描述粘性不可压缩流体动量守恒的运动方程(简称N-S方程)并作了大量简化的基础上,Reynolds导出了描述润滑膜压力分布的Reynolds方程,从而奠定了流体动力润滑理论的原始基础[1-2]。通常的摩擦副的润滑求解,是在层流假设条件进行,而超出此求解范围(如小膜厚比下),准确的润滑求解需要使用N-S方程。为了全解N-S方程,1972年,Patankar等[3]提出了一种压力耦合方程的半隐式计算格式,即SIMPLE算法,成功解决了流场N-S方程中压力与速度的耦合问题。随着计算科学的快速发展,目前出现了一些CFD商业软件[4-6]。就流体润滑分析而言,主要使用的软件有CFX和Fluent,求解控制方程时,二者采用了较为高效的方法(如全隐式多网格耦合方法和SIMPLE算法),在流固耦合问题的求解上具有一定优势。2000年,Chen等[7]利用CFX分析了滑动轴承侧隙对油膜阻尼性能的影响;2005年,Guo等[8]利用CFD软件分析了滑动轴承及挤压油膜阻尼器的静态性及动态特性;2008年,Gertzos等[9]利用Fluent对采用宾汉润滑剂的滑动轴承进行了流体动力润滑计算,Cupillard等[10]利用CFX对具有表面微造型的滑动轴承进行了CFD分析,Almqvist等[11]利用CFX分析了热瞬变粗糙弹流润滑线接触问题;2009年,Cupillard等[12-13]利用CFX对具有纹理的滑块进行了三维热流体动力学分析,对具有纹理的流体动力学接触中的惯性效应进行了分析,Hu等[14]利用CFX对具有微造型的滑动轴承进行了润滑行为分析。在国内,2008年,高庆水等[15]利用Fluent对液体动压滑动轴承进行了动特性研究;2010年,林起崟等[16]利用Fluent对高速滑动轴承进行了流固耦合传热及流场分析,张楚等[17]利用Fluent进行了基于两相流理论的滑动轴承流场计算分析;2011年,涂林等[18]利用Fluent对动压径向轴承油膜力场进行了模拟研究。以上文献借助CFD软件在轴承润滑领域做出了有益的探索,然而均未对不同软件在滑动轴承润滑计算中的异同进行分析。由于在润滑计算中,不同软件对于某些问题的处理方式不尽相同,这将可能导致计算结果存在一定差异。因此,分析不同软件润滑计算差异十分必要。笔者以径向滑动轴承流体动力润滑油膜为研究对象,对比分析了ANSYS Workbench 12.1中两种CFD模块CFX和Fluent的润滑计算结果异同,以为使用上述软件进行润滑分析提供参考。
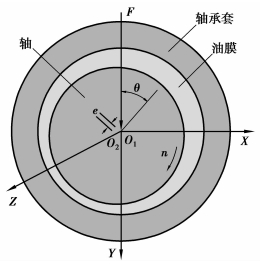
1 物理模型选取径向滑动轴承润滑为研究对象,滑动轴承系统如图 1所示。其中,X、Y、Z分别为轴承径向、垂向和宽度方向。轴承直径D为35 mm,半径间隙C为35 μm,液相、蒸汽相润滑油的密度分别为870 kg/m3和1.2 kg/m3,液相、蒸汽相润滑油的动力粘度分别为0.035 Pa·s和2×10-5 Pa·s。分别分析其在不同偏心率ε、转速n及长径比等工况下稳定运转时的摩擦学性能。使用CFX和Fluent分析时,对轴承的两个端面分别施加压力入口边界条件和压力出口边界条件,边界压力均为环境压力值;对油膜内表面施加旋转壁面边界条件,旋转方向如图 1所示,具体大小由工况而定;对油膜外表面施加固定壁面边界条件。
|
图 1 滑动轴承系统示意图 |
不考虑温度因素对滑动轴承润滑油膜流场的影响,并假设流动状态为层流,油膜区域内的流体(润滑油)须同时满足质量守恒方程和动量方程。
2.1 质量守恒方程CFX和Fluent在进行计算流体动力学分析时,均首先将流体区域划分为有限个流体微团,再对每一微团进行分析。将润滑油视为不可压缩流体,流场中各流体微团均须满足连续性条件,即质量守恒方程[19-20]
| $ \frac{{\partial {\rho _{\rm{m}}}}}{{\zeta t}} + \nabla \cdot({\rho _{\rm{m}}}{\mathit{\boldsymbol{v}}_{\rm{m}}}) = 0, $ | (1) |
式中:润滑油混合物平均密度ρm=αlρl+αvρv,αl与αv分别为液相、蒸汽相润滑油的体积百分比,且满足αl+αv=1,ρl与ρv分别为液相、蒸汽相润滑油的密度;两相质量加权平均速度vm=(αlρlvl+αvρvvv)/ρm,vl与vv分别为液相、蒸汽相润滑油的流速。
2.2 动量方程除满足质量守恒方程之外,润滑油运动同时也应满足动量方程
| $ \begin{array}{l} \frac{\partial }{{\partial t}}({\rho _{\rm{m}}}{\mathit{\boldsymbol{v}}_{\rm{m}}}) + \nabla \cdot({\rho _{\rm{m}}}{\mathit{\boldsymbol{v}}_{\rm{m}}}{\mathit{\boldsymbol{v}}_{\rm{m}}}) = \\ - \nabla p + \nabla \cdot[{\mu _{\rm{m}}}(\nabla {\mathit{\boldsymbol{v}}_{\rm{m}}} + \nabla {\mathit{\boldsymbol{v}}_{\rm{m}}}^{\rm{T}})] + \\ \nabla \cdot({\alpha _{\rm{l}}}{\rho _{\rm{l}}}{\mathit{\boldsymbol{v}}_{{\rm{dr}},{\rm{l}}}}{\mathit{\boldsymbol{v}}_{{\rm{dr}},{\rm{l}}}} + {\alpha _{\rm{v}}}{\rho _{\rm{v}}}{\mathit{\boldsymbol{v}}_{{\rm{dr}},{\rm{l}}}}{\mathit{\boldsymbol{v}}_{{\rm{dr}},{\rm{l}}}}), \end{array} $ | (2) |
式中:润滑油平均动力粘度μm=αlμl+αvμv,μl与μv分别为液相、蒸汽相润滑油的动力粘度;vdr, l与vdr, l分别为液相、蒸汽相润滑油的漂移速度,vdr, l=vl-vm及vdr, l=vv-vm。
由于发散间隙区域油膜压力为非正值,这将导致油膜破裂从而发生气穴现象,笔者基于两相流模型分析了气穴因素的影响[21-23]。当流场压力为负值时,液相润滑油汽化为润滑油蒸汽,同时也伴随有润滑油蒸汽凝聚为液相润滑油的过程。当油压为饱和蒸汽压力值时,两相润滑油间的相互转化达到动态平衡,各相成分值处于稳定值。这里采用Rayleigh-Plesset模型描述了气穴中气泡的变化情况。
2.3 摩擦学性能参数计算出润滑油膜流场分布数据后,即可分别求得轴承承载力、摩擦力及摩擦系数等摩擦学性能参数。
对油膜压力在润滑油与轴承套的接触面上进行积分即得轴承承载力
| $ W = \frac{D}{2}\sqrt {{{(\int {\int\limits_A p } \;{\rm{sin}}\;{\mathit{\Phi }} {\rm{d}}{\mathit{\Phi }} {\rm{d}}z)}^2} + {{(\int {\int\limits_A p } \;{\rm{cos}}\;{\mathit{\Phi }} {\rm{d}}{\mathit{\Phi }} {\rm{d}}z)}^2}} , $ | (3) |
式中:D为轴承直径;p为润滑油膜压力;Φ、z分别为周向、轴向坐标;A为润滑油膜与轴承套的接触面。
在润滑油与轴承套的接触面上,由粘滞力引起的摩擦力
| $ {F_{\rm{f}}} = \frac{D}{2}\int {\int\limits_A \tau } {\rm{d}}{\mathit{\Phi }} {\rm{d}}z $ | (4) |
式中τ为润滑油膜与轴承套接触面上的剪应力。
由以上求得的轴承承载力和摩擦力即可计算摩擦系数
| $ f = \frac{{{F_{\rm{f}}}}}{W}。$ | (5) |
CFX和Fluent均采用迭代法求解上述质量守恒方程和动量方程,计算过程中当残差小于给定收敛精度值时,迭代停止。CFX中对残差的定义为
| $ {\mathit{\boldsymbol{r}}^I} = \mathit{\boldsymbol{b}} - \mathit{\boldsymbol{A}}{\varphi ^I}, $ | (6) |
式中:rI为第I次迭代计算后所得的残差;b为方程(1)及方程(2)离散并线性化后的常数项;A为系数矩阵;φI为待求量(压力、速度)第I次迭代计算值。对残差做规则化处理
| $ \left[ {{{\mathit{\boldsymbol{\tilde r}}}_\varphi }} \right] = \frac{{\left[ {{\mathit{\boldsymbol{r}}_\varphi }} \right]}}{{{a_p}\Delta \varphi }}, $ | (7) |
式中:aP为控制体积相应系数;Δφ为变量范围。仿真计算时,选取判断收敛的指标为求解域每一控制体积计算残差的均方根值。
Fluent中残差的定义为
| $ {\mathit{\boldsymbol{r}}_\varphi } = \frac{{{\Sigma _{{\rm{cell}}P}}\left| {{\Sigma _{{\rm{nb}}}}{a_{{\rm{nb}}}}{\varphi _{{\rm{nb}}}} - {a_{\rm{P}}}{\varphi _{\rm{P}}}} \right|}}{{{\Sigma _{{\rm{cell}}P}}\left| {{a_{\rm{P}}}{\varphi _{\rm{P}}}} \right|}}, $ | (8) |
式中:anb与φnb为周围控制体积的影响系数和待求量值;aP与φP分别为当前控制体积的求解系数和待求量值。由式(8)可知,与CFX不同,Fluent判断收敛的指标为整个求解域的计算残差。
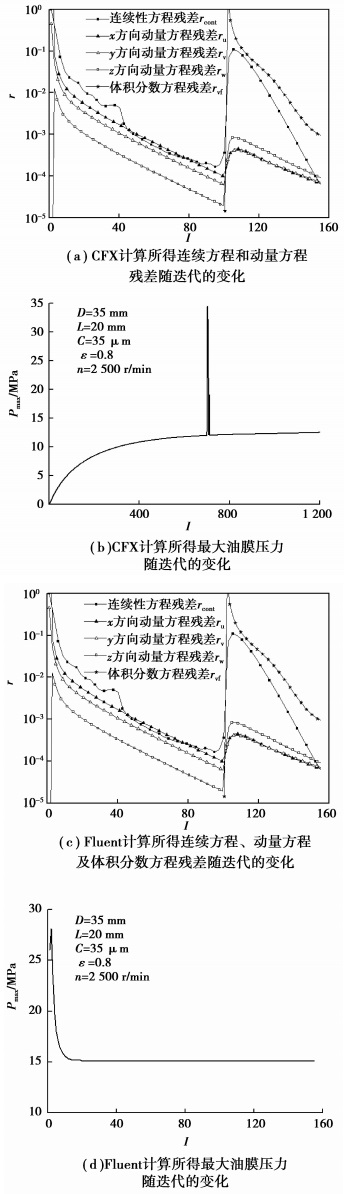
实际求解过程中,由于模型、计算小数位取舍等诸多原因,残差可能将最终保持在某一值附近,此时可通过判断滑动轴承润滑油膜流场特征参数(如最大油膜压力Pmax、最大润滑油流速vmax等)来确定其收敛情况。当特征参数值趋于稳定时,亦可认为求解收敛。此外,还可通过轴承润滑油流量守恒来判断收敛。本研究中,将残差精度设置为10-3,同时根据最大油膜压力Pmax变化来判断收敛。此外,处理气穴的方法为先不考虑气穴的影响,求解得到一个流场初值后再考虑气穴因素,由此可更好保证求解的收敛性且有效缩短求解时间。两种模块计算所得的收敛曲线如图 2所示,其中I表示迭代次数,r表示残差。
|
图 2 CFX和Fluent计算收敛的变化 |
由图 2可知,使用前表述的参数和边界条件,CFX计算迭代至700步时,各控制方程残差值、最大油膜压力值均大幅增大(此为加入气穴模型的缘故),随后趋于稳定。Fluent计算迭代至100步时控制方程残差亦有相同变化,其变化也是由于加入气穴模型引起的。此外,CFX和Fluent计算所得的收敛曲线存在一定差异,如Fluent计算所得最大油膜压力收敛较快。其原因为:CFX采用基于有限元的有限体积法对求解域进行离散,采用全隐式多网格耦合方法求解控制方程,判断收敛的指标为求解域每一控制体积计算残差的均方根值,而Fluent采用有限体积法对求解域进行离散,本研究中采用SIMPLE算法求解控制方程,判断收敛的指标为整个求解域的计算残差。
3.2 网格灵敏度分析由于滑动轴承润滑油膜膜厚方向尺寸远小于轴承周向及轴向尺寸,而网格划分的优劣将对仿真计算结果产生直接影响,故须建立高质量的网格模型。利用ICEM CFD模块划分网格,可较容易地控制各个方向的网格划分密度,以期得到高质量的计算网格模型。网格模型如图 3所示(为便于显示,网格已作稀疏化处理)。此外,为更好地反映流场膜厚方向的流动情况,膜厚方向(Y向)至少布置10层网格。
|
图 3 润滑油膜网格模型 |
网格密度对仿真计算结果具有一定影响,过于稀疏的网格可能导致求解无法收敛,而过于密集的网格又增加了求解时间。故为同时保证求解的收敛性和经济性,有必要首先进行网格灵敏度分析,以获得最佳网格密度。本研究中选取轴承长度L为20 mm,偏心率ε为0.8,转速n为2 500 r/min的模型,分别研究了周向(以c表示)、轴向(以a表示)和径向(以r表示)的网格灵敏度对最大油膜压力的影响,分析数据如表 1、2及3所示。根据表中仿真结果,选择最佳网格密度为(c,a,r)=(600,40,15),对应计算结果与各组最大网格密度模型结果的相对偏差均小于2%,可认为其合理[24]。
| 表 1 周向网格灵敏度分析 |
| 表 2 轴向网格灵敏度分析 |
| 表 3 径向网格灵敏度分析 |
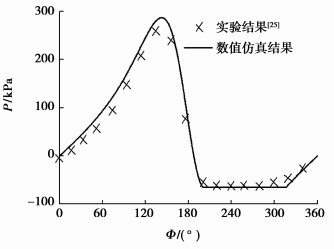
笔者采取与Jakobsson等[25]的实验数据对比方法对数值仿真计算进行了相同工况下的有效性验证。文献中轴承受到2 250 N的外载,气穴饱和压力为20 kPa。比较所得的油膜压力如图 4所示,图中轴承轴向相对坐标Z/L=0.1。可见本研究所得的压力和实验数据吻合较好(压力相对百分比偏差均小于0.5%)。这说明本研究建模的正确性,因此使用本文的轴承模型和方法可进行其他工况和几何参数下CFX和Fluent仿真结果的比较。
|
图 4 数值仿真与实验结果的油膜压力曲线对比 |
进行不同偏心率ε下的润滑对比计算时,所采用轴承的长度L为20 mm,ε分别为0.4、0.5、0.6、0.7及0.8,转速n为2 500 r/min。进行不同转速工况下的润滑对比计算时,所采用轴承的长度L为20 mm,偏心率ε为0.8,转速n分别为1 000、1 500、2 000、2 500及3 000 r/min。进行不同长径比工况下的润滑对比计算时,所采用轴承的偏心率ε为0.8,转速n为2 500 r/min,长径比L/D分别为0.6、0.8、1.0、1.2及1.4(轴承直径D为35 mm,长度L分别为21、28、35、42及49 mm)。分别建立如上述参数的仿真模型,采用CFX和Fluent计算滑动轴承相关的摩擦学性能。
4 结果及讨论 4.1 不同偏心率下比较不同偏心率ε下滑动轴承的摩擦学性能比较如图 5所示。可见,两种模块计算所得的最大油膜压力及承载力均随ε的增大而增大,这与文献[8]结论一致,但相对于Fluent,CFX计算结果较小,且二者差异随着ε的增大而增大。由于承载力通过油膜压力积分得到,故其变化规律与最大油膜压力相同。由图 5(c)可以看出,CFX和Fluent计算所得的摩擦力也均随ε的增大而增大,在ε为0.6时差异较大。两种模块计算所得的摩擦系数(图 5(d))均随ε的增大而减小,CFX计算结果在ε为0.4时小于Fluent,其他偏心率时反之。计算偏差的产生与两种模块在求解控制方程时所采用的不同离散方法、不同求解方法及收敛判断准则的选取有关。由此可见:在小偏心率工况下,CFX和Fluent的计算结果更为接近,随着偏心率的增大,二者计算结果偏差增大。
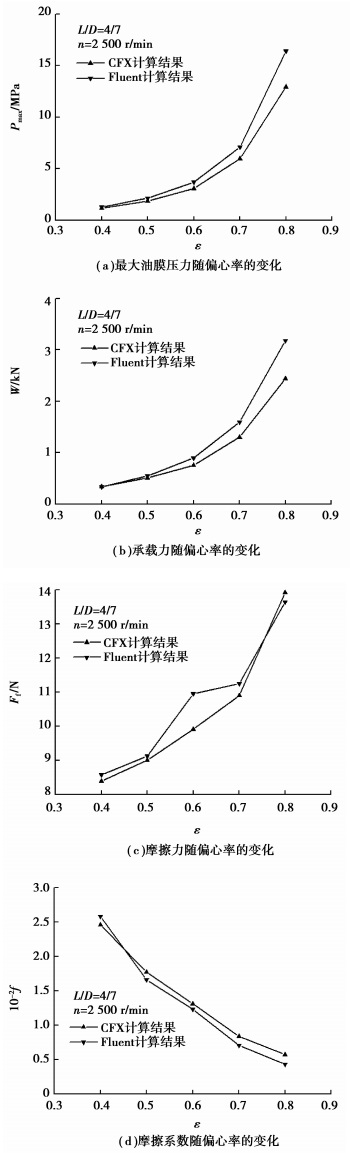
|
图 5 不同偏心率工况下滑动轴承的摩擦学性能参数 |
不同转速n下滑动轴承的摩擦学性能比较如图 6所示。CFX与Fluent计算所得的偏位角(图 6(a))随n的增大而无明显变化,这与文献[26]结论一致,但相对于Fluent,CFX计算结果偏大。两种模块计算所得的最大油膜压力(图 6(b))及承载力(图 6(c))均随n的增大而增大,这与文献[18]结论一致,但相对于Fluent,CFX计算结果偏小。二者计算所得的摩擦力(图 6(d))均随转速的增大而近似线性增大。对于摩擦系数(图 6(e)),随着n的增大,CFX计算结果略有减小而Fluent计算结果几乎不改变。在相同转速下,相对于Fluent,CFX计算所得的摩擦系数偏大,且偏差随转速的增大而减小。这同样是由于两种模块求解控制方程时所采用的不同方法以及所选取的迭代收敛准则不同造成。由此可见:CFX和Fluent在高转速下所得的结果更为接近,且二者在小转速下偏差较大。
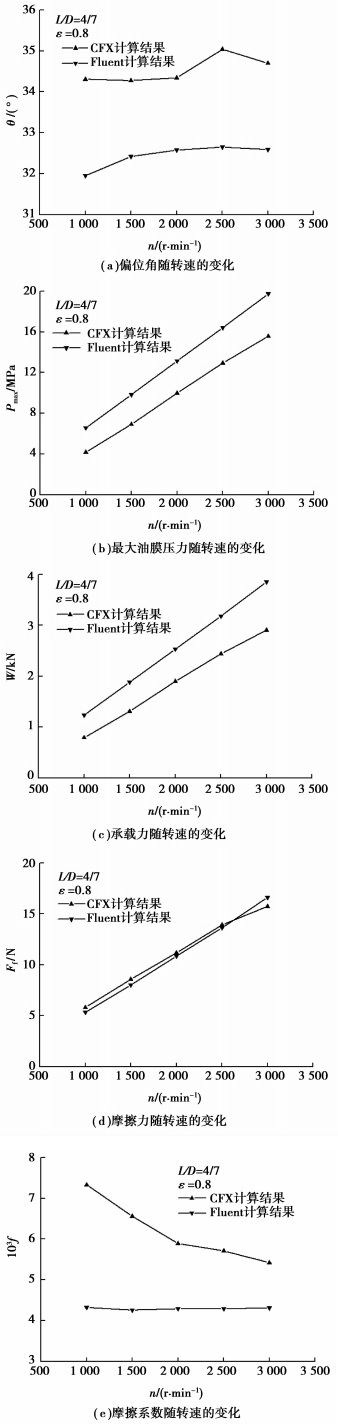
|
图 6 不同转速工况下滑动轴承的摩擦学性能参数 |
不同长径比L/D下滑动轴承的摩擦学性能比较如图 7所示。CFX和Fluent计算所得的偏位角(图 7(a))及摩擦力(图 7(d))均随L/D的增大而增大,与文献[26]结论一致,但相对于Fluent,CFX计算得到的结果偏大。由图 7(b)和7(c)可以看出,在相同L/D下,CFX得到的最大油膜压力与承载力均小于Fluent得到的相应值。但前者得到的摩擦系数大于后者,且偏差随L/D的增大而减小。这同样是因两种模块采用的控制方程(式(1)及式(2))的离散和求解方法以及收敛准则不同。综上所述,CFX和Fluent在计算大长径比工况问题所得的结果更为接近;随长径比的减小,二者计算偏差增大。
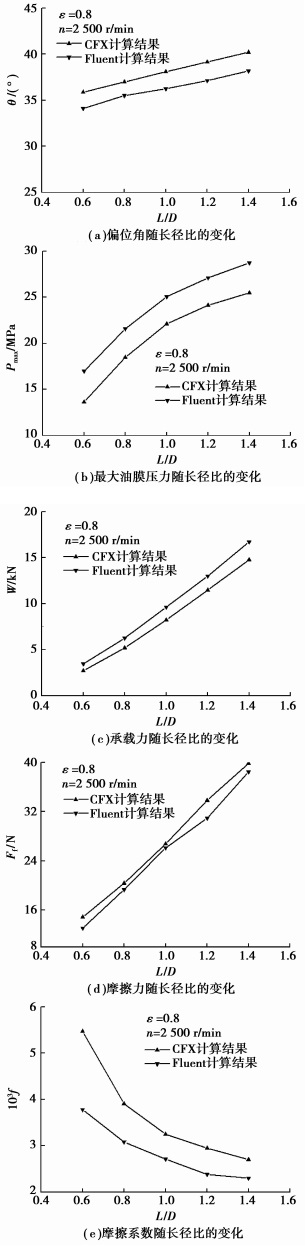
|
图 7 不同长径比工况下滑动轴承的摩擦学性能参数 |
笔者比较了使用ANSYS的CFD模块CFX与Fluent计算得到的滑动轴承的摩擦学性能,结论如下:
1) CFX和Fluent对滑动轴承进行润滑计算结果虽有偏差,但就总体趋势而言,二者所得结果基本吻合。
2) CFX计算所得最大油膜压力及轴承承载力的值小于Fluent的计算结果,而摩擦系数大于后者所得结果。
3) CFX和Fluent计算结果偏差受偏心率、转速及长径比等因素影响,且二者在大偏心率、小转速、小长径比工况下的计算幅值偏差相对较大。
4) 本文研究的算例虽然有限,但所得结论仍可为轴承润滑计算工作者在上述两种模块选择问题上提供有益的参考,笔者将在后续研究中计入轴承套与润滑油间的流固耦合作用、润滑油的热效应等因素的影响。
| [1] | Reynolds O. On the theory of lubrication and its application to Mr. Bearchamp tower's experiments, including an experimental determination of the viscosity of olive oil[J]. Philosophical Transactions of the Royal Society of London, 1886, 177: 157–234. DOI:10.1098/rstl.1886.0005 |
| [2] | 张直明. 滑动轴承的流体动力润滑理论[M]. 北京: 高等教育出版社, 1986. |
| [3] | Patankar S V, Spalding D B. A calculation procedure for heat, mass and momentum transfer in three-dimensional parabolic flows[J]. International Journal of Heat and Mass Transfer, 1972, 15(10): 1787–1806. DOI:10.1016/0017-9310(72)90054-3 |
| [4] | 王福军. 计算流体动力学分析:CFD软件原理与应用[M]. 北京: 清华大学出版社, 2004. |
| [5] |
姚征, 陈康民.
CFD通用软件综述[J]. 上海理工大学学报, 2002, 24(2): 137–144.
YAO Zheng, CHEN Kangmin. Review on the commercial CFD softwares[J]. Journal of University of Shanghai for Science and Technology, 2002, 24(2): 137–144. (in Chinese) |
| [6] |
翟建华.
计算流体力学(CFD)的通用软件[J]. 河北科技大学学报, 2005, 26(2): 160–165.
ZHAI Jianhua. Review of commercial CFD software[J]. Journal of Hebei University of Science and Technology, 2005, 26(2): 160–165. DOI:10.7535/hbkd.2005yx02021 (in Chinese) |
| [7] | Chen P Y P, Hahn E J. Side clearance effects on squeeze film damper performance[J]. Tribology International, 2000, 33(3/4): 161–165. |
| [8] | Guo Z L, Hirano T, Kirk R G. Application of CFD analysis for rotating machinery:Part Ⅰ:hydrodynamic, hydrostatic bearings and squeeze film damper[J]. Journal of Engineering for Gas Turbines and Power, 2005, 127(2): 445–451. DOI:10.1115/1.1807415 |
| [9] | Gertzos K P, Nikolakopoulos P G, Papadopoulos C A. CFD analysis of journal bearing hydrodynamic lubrication by Bingham lubricant[J]. Tribology International, 2008, 41(12): 1190–1204. DOI:10.1016/j.triboint.2008.03.002 |
| [10] | Cupillard S, Glavatskih S, Cervantes M J. Computational fluid dynamics analysis of a journal bearing with surface texturing[J]. Engineering Tribology, 2008, 222: 97–107. |
| [11] | Almqvist T, Larsson R. Thermal transient rough EHL line contact simulations by aid of computational fluid dynamics[J]. Tribology International, 2008, 41(8): 683–693. DOI:10.1016/j.triboint.2007.11.004 |
| [12] | Cupillard S, Glavatskih S, Cervantes M J. 3D thermohydrodynamic analysis of a textured slider[J]. Tribology International, 2009, 42(10): 1487–1495. DOI:10.1016/j.triboint.2009.05.021 |
| [13] | Cupillard S, Glavatskih S, Cervantes M J. Inertia effects in textured hydrodynamic contacts[J]. Journal of Engineering Tribology, 2010, 224(8): 751–756. |
| [14] | Hu Y, Balendra R. CFD analysis on the lubrication behaviours of journal bearing with dimples[C]//Proceedings of the International Conference on Mechatronics and Automation, August 9-12, 2009, Changchun, China. Piscataway:IEEE Press, 2009:1279-1284. |
| [15] |
高庆水, 杨建刚.
基于CFD方法的液体动压滑动轴承动特性研究[J]. 润滑与密封, 2008, 33(9): 65–67.
GAO Qingshui, YANG Jiangang. Research on the dynamic characteristics of hydrodynamical journal bearing based on CFD analysis[J]. Lubrication Engineering, 2008, 33(9): 65–67. (in Chinese) |
| [16] |
林起崟, 魏正英, 唐一平, 等.
高速滑动轴承流固耦合传热及流场分析[J]. 润滑与密封, 2010, 35(10): 28–32, 58.
LIN Qiyin, WEI Zhengying, TANG Yiping, et al. Analysis on the fluid/solid coupled heat transfer and flow field of high-speed sliding bearings[J]. Lubrication Engineering, 2010, 35(10): 28–32, 58. DOI:10.3969/j.issn.0254-0150.2010.10.008 (in Chinese) |
| [17] |
张楚, 杨建刚, 郭瑞, 等.
基于两相流理论的滑动轴承流场计算分析[J]. 中国电机工程学报, 2010, 30(29): 80–84.
ZHANG Chu, YANG Jiangnag, GUO Rui, et al. Simulation of journal bearing flow field using computational fluid dynamics two phase flow theory[J]. Proceedings of the CSEE, 2010, 30(29): 80–84. (in Chinese) |
| [18] |
涂林, 李多民, 段滋华.
基于Fluent的动压径向轴承油膜力场模拟研究[J]. 润滑与密封, 2011, 36(4): 82–86.
TU Lin, LI Duomin, DUAN Zihua. Pressure field numerical simulation of hydrodynamic bearing based on fluent[J]. Lubrication Engineering, 2011, 36(4): 82–86. (in Chinese) |
| [19] | ANSYS. ANSYS CFX introduction. release 12.1[EB/OL].[2012-02-19]. http://www.doc88.com/p-300881926603.html. |
| [20] | ANSYS. ANSYS fluent 12.0 theory guide[EB/OL].[2012-02-21]. http://www.docin.com/p-123169887.html. |
| [21] | Kumar P S, Pandit A B. Modeling hydrodynamic cavitation[J]. Chemical Engineering & Technology, 1999, 22(12): 1017–1027. |
| [22] | Bakir F, Rey R, Gerber A G, et al. Numerical and experimental investigations of the cavitating behavior of an inducer[J]. International Journal of Rotating Machinery, 2004, 10(1): 15–25. DOI:10.1155/S1023621X04000028 |
| [23] |
孙丹, 杨建刚, 郭瑞.
基于局部微分求积[XC半字线.tif, JZ]拉格朗日法的滑动轴承动力特性求解模型[J]. 中国电机工程学报, 2011, 31(14): 90–95.
SUN Dan, YANG Jiangang, GUO Rui. Journal bearing dynamic characteristics calculation model based on the local differential quadrature-lagrange method based on lagrange interpolation method[J]. Proceedings of the CSEE, 2011, 31(14): 90–95. (in Chinese) |
| [24] | Liu H, Xu H, Ellison P J, et al. Application of computational fluid dynamics and fluid-structure interaction method to the lubrication study of a rotor-bearing system[J]. Tribology Letters, 2010, 38: 325–336. DOI:10.1007/s11249-010-9612-6 |
| [25] | Jakobsson B, Floberg L. The finite journal bearing, considering vaporization:das gleitlager von endlicher breite mit verdampfung[M].[S.l.]:Gumperts F rlag, 1957. |
| [26] |
康宁, 迟启明.
基于N-S方程的径向滑动轴承油膜承载力的计算[J]. 润滑与密封, 2010, 35(10): 9–12.
KANG Ning, CHI Qiming. Calculation of oil film load of radial sliding bearing based on N-S equation[J]. Lubrication Engineering, 2010, 35(10): 9–12. DOI:10.3969/j.issn.0254-0150.2010.10.003 (in Chinese) |
 2013, Vol. 36
2013, Vol. 36

