2. 中国汽车工程研究院有限公司 汽车噪声振动和安全技术国家重点实验室, 重庆 400039
2. State Key Laboratory of Vehicle NVH and Safety Technology, China Automotive Engineering Research Institute Co., Ltd., Chongqing 400039, China
凸轮机构是发动机配气机构的重要元件,起到定时开启和关闭各缸进、排气门的作用。随着科技的发展,气门运动规律、气门反跳、凸轮从动件的飞脱、凸轮与挺柱的接触应力等方面的问题已经得到了深入的研究和解决[1-4]。而由于凸轮轴在工作过程中受到由气门经挺柱传来的各缸燃气爆发引起的冲击载荷、以及由皮带传来的曲轴转速的波动影响,使得凸轮轴在工作中常出现振动而产生噪音,继而影响正时轮系的运动控制[5]。同时凸轮轴负载扭矩作为正时轮系设计和分析的边界条件,其计算准确性对正时轮系的设计影响很大。
孙鋆强等[6]研究了由于从动件对凸轮轴的作用使凸轮轴产生扭转变形及其对振动的影响。谢黎明等[7]研究了凸轮轴的扭转刚度引起的凸轮轴角速度变化,进而导致的系统振动和传递误差。唐林虎等[8]研究了高速时由于凸轮的离心激励引起的强迫振动,认为消除凸轮负载系统的动不平衡量是减小凸轮负载系统振动的措施。王远等[9]计算了发动机凸轮轴承受的动载荷,并对凸轮轴进行了强度评价和疲劳特性分析。Saka等[10]对凸轮轴的扭转振动进行了分析,认为其扭转是由于挺柱与凸轮轴之间不断变化的接触力造成的,而凸轮轴的振动又会反过来影响挺柱的运动及两者之间的接触力。Teodorescu等[11]研究了凸轮轴扭转振动对配气机构动态特性的影响。还有一些在研究配气机构动态特性时,建立了考虑凸轮轴扭转振动和弯曲振动的模型[12-15]。以上文献表明,目前国内外对凸轮轴振动的研究主要集中在两方面:1)对凸轮轴的扭转振动的研究。2)在对整个配气机构的研究中,将凸轮轴的振动考虑为一个影响因素。目前的研究方法主要基于简化的数学模型或多体动力学模型,应用有限元模型对凸轮轴进行振动分析的研究并不多见;而在对凸轮轴载荷的研究中,准确的凸轮轴负载扭矩的计算公式,还未见相关的文献报道。
笔者以某发动机进气凸轮系统为研究对象,对凸轮轴进行了受力分析,推导出了凸轮轴负载扭矩的理论计算公式,并通过与瞬态仿真结果的对比,验证了理论公式的正确性和有限元方法的正确性。然后结合瞬时约束模态与瞬态有限元分析,得到了凸轮轴在燃气爆发压力作用下的振动特性。结果表明,凸轮轴振动主要是弯曲振动,凸轮轴各个部分发生弯曲共振的程度并不相同,凸轮轴轴承座的宽度对凸轮轴的弯曲振动影响很大。该研究对凸轮机构的振动研究具有普遍意义,能有效指导凸轮机构的设计和振动控制。
1 凸轮轴负载扭矩计算直列四缸发动机各缸是按照一定顺序循环工作的,其相位差为90°, 为了使分析更清楚简单,选择进气凸轮气门机构中的单个凸轮负载气门机构进行分析。
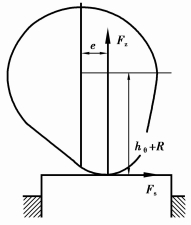
1.1 凸轮轴负载扭矩理论公式推导图 1是单个凸轮直接负载气门的受力分析, 凸轮轴的负载扭矩计算式为
| $ T = {F_{\rm{z}}}\cdot e + {F_{\rm{s}}}({h_\theta } + R), $ | (1) |
|
图 1 凸轮受力分析示意图 |
式中:Fz为接触点的负荷;Fs为挺柱与凸轮的摩擦力;e为接触点的偏心量;hθ为气门升程;R为凸轮基圆半径。
接触点的负荷包括气门弹簧的负荷、气门机构惯性力及气门受到的燃气爆发压力,其计算公式为
| $ {F_{\rm{z}}} = K({h_\theta } + \Delta x) + \left( {{m_{\rm{v}}} + \frac{{{m_s}}}{3}} \right){\omega ^2}\frac{{{{\rm{d}}^2}{h_\theta }}}{{{\rm{d}}{\theta ^2}}} + P\cdot S, $ | (2) |
| $ {F_{\rm{s}}} = {\mu _{\rm{c}}}\cdot {F_{\rm{z}}}, $ | (3) |
| $ e = \frac{{{\rm{d}}{h_\theta }}}{{{\rm{d}}\theta }}, $ | (4) |
式中:K为气门弹簧刚度;Δx为气门弹簧的压缩量;P为气门处的燃气爆发压强;S为气门的截面积;ω为凸轮轴角速度;μc为凸轮与挺柱的摩擦系数。将式(2)、(3)、(4)带入式(1)得到计算凸轮轴负载扭矩的关系式为
| $ \begin{array}{c} T = \left[ {K({h_\theta } + \Delta x) + \left( {{m_{\rm{V}}} + \frac{{{m_{\rm{s}}}}}{3}} \right) \cdot \frac{{{{\rm{d}}^2}{h_\theta }}}{{{\rm{d}}{\theta ^2}}} \cdot {\omega ^2} + P \cdot S} \right] \cdot \\ \left[ {\frac{{{\rm{d}}{h_\theta }}}{{{\rm{d}}\theta }} + {\mu _c}({h_\theta } + R)} \right]。\end{array} $ |
该公式也可应用于多缸发动机的凸轮轴负载扭矩的计算,凸轮轴所受总扭矩即为对应相同时刻的各缸扭矩之和。
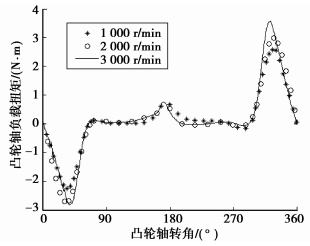
1.2 实例计算根据上述公式对某直列四缸发动机配气凸轮机构在凸轮轴1 000、2 000、3 000 r/min转速下的单个配气凸轮轴负载扭矩进行计算,得到以上各转速下的凸轮轴负载扭矩随凸轮轴转角的关系曲线如图 2所示。
|
图 2 凸轮轴负载扭矩理论计算值 |
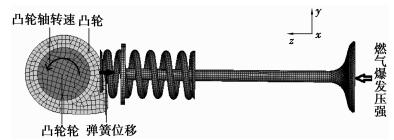
为了验证理论公式计算结果的正确性,对单个凸轮的模型进行了有限元分析,相关边界条件和载荷的施加如图 3所示(分析中忽略凸轮轴的转速波动)。
|
图 3 单个凸轮负载气门瞬态分析模型 |
经瞬态仿真分析,得到了不同转速下凸轮轴所受到的来自气门挺柱向上的接触力Fz和沿凸轮速度切线方向的接触力Fs,根据公式
| $ T = {F_{\rm{z}}}\cdot e + {F_{\rm{s}}}({h_\theta } + R), $ |
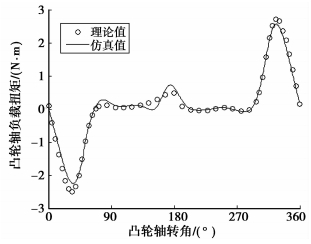
计算得到各个转速下凸轮轴负载扭矩,将其与理论计算值对比,结果如图 4~图 6所示。
|
图 4 凸轮轴1 000 r/min负载扭矩对比 |
|
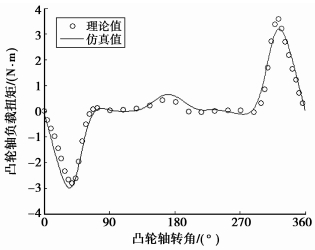
图 5 凸轮轴2 000 r/min负载扭矩对比 |
|
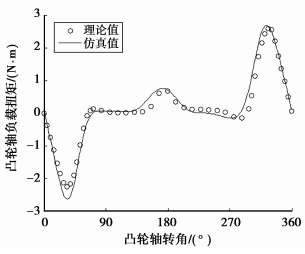
图 6 凸轮轴3 000 r/min负载扭矩对比 |
对比图 4~6可知,凸轮轴负载扭矩的理论公式计算值和有限元分析结果在峰值上差异很小,趋势上吻合良好,这说明所推导的理论公式是正确的,同时也验证了瞬态有限元模型的正确性。
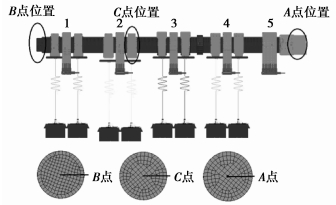
2 凸轮轴振动特性分析 2.1 凸轮轴振动瞬态分析为了研究凸轮轴在燃气爆发压力作用下的振动[16],在图 3模型的基础上,建立了整个发动机配气凸轮机构瞬态有限元分析模型,如图 7所示。图中点A、B、C为计算结果的振动加速度测点,他们位于凸轮轴的轴线上。
|
图 7 凸轮机构整体有限元模型 |
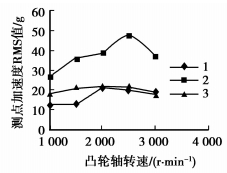
图 8所示为凸轮轴转速为1 000、1 500、2 000、2 500、3 000 r/min时A、B、C 3个测点的加速度RMS值随转速变化的关系曲线。由图可知,凸轮轴B端的振动最大,气门压力施加处C点的振动随速度变化较平稳,A端点在低速时振动较小,整体上波动明显。
|
图 8 测点RMS值随转速变化曲线 |
为了进一步揭示凸轮轴振动原因,对凸轮轴进行了瞬时约束模态分析。瞬时约束模态是指凸轮轴与凸轮轴轴承座在某些时刻由于受燃气爆发压力而紧密贴紧时的模态。凸轮轴每转一周,图 7所示的轴承座1、2、3、4处将依次经历一次与凸轮轴紧密接触的机会,相应的瞬时约束模态频率和振型如表 1和图 9~12所示。
| 表 1 对应各个轴承座瞬时约束模态频率 |

|
图 9 约束1号轴承座时的前两阶模态振型 |
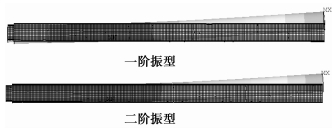
|
图 10 约束2号轴承座时的前两阶模态振型 |
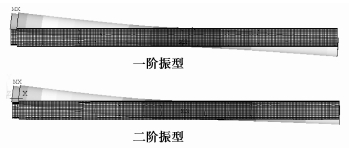
|
图 11 约束3号轴承座时的前两阶模态振型 |
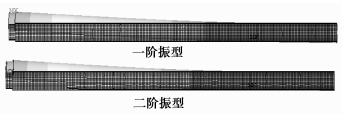
|
图 12 约束4号轴承座时的前两阶模态振型 |
为了比较各瞬时约束频率是否会与燃气爆发压力所引起的冲击载荷的频率接近,计算了凸轮轴转速1 000~3 000转时对应的冲击载荷的频率,如表 2所示。
| 表 2 凸轮轴各转速下对应的冲击载荷频率 |
对比表 1和表 2可知,轴承座1、2、4的第1、2阶瞬时约束模态频率与某些转速下的燃气爆发压力的激励载荷频率比较接近,有可能发生共振;再从图 9~12的模态振型来看,其前两阶模态均为弯曲模态,这说明如果凸轮轴发生了共振,则主要为弯曲振动。为了验证这种推测,又从瞬态分析结果中提取了凸轮轴的轴线上A点的运动轨迹,如图 13所示。
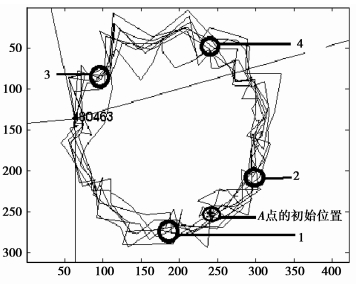
|
图 13 测点A的运动轨迹 |
由图 13可知,A点的轨迹几乎为一个圆,说明凸轮轴在转动的同时确实伴随着弯曲振动。再结合图 9~12的振型知,C点处于凸轮轴的中间位置,在各振型中几乎都处于节线及其附近区域,在燃气爆发压力作用下由于共振而引起的振动相对较小,且对转速或频率不敏感,这反映在图 8中C点的振动曲线几乎不随转速变化,很平稳;而A与B两点正好处于各阶振型的腹部区域,由于共振而引起振动的可能性较大,且对频率或转速比较敏感。而在图 8所示的仿真结果中,A点和B点的振动则随转速变化相对较大,也验证了这一点。
为了解释图 8中A、B两点的振动随转速变化的趋势,计算了它们的模态频率与激励频率之差,如表 3、4所示。
| 表 3 B点模态频率与激励频率关系 |
| 表 4 A点模态频率与激励频率关系 |
对比图 8和表 3可知,在1 000、1 500转时,Δf相差较远,不易共振,A点对应这两个转速的振动也相对较小;2 000转时Δf相差仅2 Hz,故振动很快上去;2 500转和3 000转时Δf相差逐渐增大,振动又下来了。
用同样的方法来分析图 8中B点曲线和表 4可知,在整个转速范围内,Δf相差都不大,故B点曲线各转速的振动均比较大,尤其在2 500转时,Δf相差仅6 Hz,加之此时转速高,使振动达到了最大。
3 凸轮轴振动控制分析通过以上分析知,凸轮轴的振动形态是一种弯曲振动,且振动大是因为发生了一定程度的共振。因此,要减小凸轮轴由弯曲共振引起的振动,就要想办法使凸轮轴工作时的瞬时约束模态避开各个转速下冲击载荷的频率。实现这一目标的措施很多,笔者尝试加宽和减窄其轴承座的宽度来提高或降低其瞬时约束模态频率大小,希望它远离激励频率。
图 7所示模型中共有5个轴承座,对这些轴承座施加了如下措施:
1) 将轴承座宽度均加宽2 mm;
2) 将轴承座宽度均减小到初始模型的1/3。分别对以上2种模型进行了瞬时约束模态分析,如表 5、6所示。
| 表 5 加宽轴承座后凸轮轴约束模态频率 |
| 表 6 减小轴承座后凸轮轴约束模态频率 |
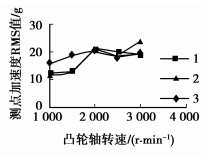
同时,也计算增加和减窄轴承座时凸轮轴的瞬态响应,得到了A、B两点对应的加速度RMS值随转速变化的关系曲线,如图 14、15所示,其中曲线1、2、3分别表示初始模型的计算结果、轴承座加宽后的计算结果、轴承座减窄后的计算结果。表 7和表 8分别表示初始模型、轴承座加宽后模型以及轴承座减窄后模型在各转速位置处凸轮轴上A点和B点的约束模态频率和激励频率之差。
|
图 14 A点RMS值随转速变化曲线 |
|
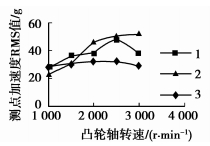
图 15 B点RMS值随转速变化曲线 |
| 表 7 A点模态频率与激励频率之差 |
| 表 8 B点模态频率与激励频率关系 |
结合图 14和表 7分析可知,轴承座3、4的宽度减小,对抑制凸轮轴高转速的振动有微小的作用,但会显著提高其低速的振动。实际中,可根据低转速和高转速时对凸轮轴振动的要求来适当选择轴承座3、4的宽度。
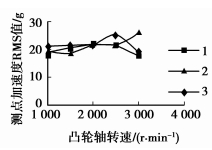
结合图 15和表 8分析可知,轴承座1、2的宽度减小,对抑制凸轮轴高速时的振动有较大作用,但会使低速的振动稍有提高。实际中,可根据低转速和高转速时对凸轮轴振动的要求来适当选择轴承座1、2的宽度。分析表明:将轴承座宽度均减小到初始模型的1/3,能实现凸轮轴A、B两点的振动在整个转速范围内基本不变。图 16再次显示C点的振动在整个转速范围随轴承座加宽和减窄基本不变,也即C点处于振型的节点区,对转速或激励频率不敏感。
|
图 16 C点RMS值随转速变化的关系曲线 |
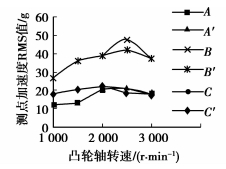
为了进一步验证上述推论,只减小1号轴承座的尺寸,对其在2 500 r/min工况下进行计算分析,结果如图 17所示,其中A、B、C表示初始模型中相应测点的计算结果;A′、B′、C′表示减小1号轴承座后相应测点的计算结果。
|
图 17 测点RMS值随转速变化曲线 |
由图 17可知,只减小1号轴承座的尺寸后,B点在2 500 r/min的工况下的振动明显降低,而A、C点振动基本不受影响。
4 结论1) 笔者通过对配气凸轮进行受力分析,推导了凸轮轴负载扭矩计算的理论公式,并用有限元仿真对理论公式的计算结果进行验证,结果显示两者吻合良好,说明理论公式和有限元分析方法均正确、可行。
2) 凸轮轴的振动主要是弯曲振动,且振动的大小与弯曲共振程度密切相关。
3) 凸轮轴两端的振动对激励的频率比较敏感,容易发生共振;而凸轮轴的中部基本在振型的节点区域,对转速或激励频率不敏感。
4) 各轴承座的宽度对凸轮轴的瞬时约束模态有较大的影响,进而影响凸轮轴在各转速下的振动大小。
5) 减小轴承座的宽度,可以降低高转速时的振动,但同时可能增大低速时的振动,可根据实际要求选择一个折中的方案。
| [1] | Rivola A, Troncossi M, Dalpiaz G, et al. Elastodynamic analysis of the desmodromic valve train of a racing motorbike engine by means of a combined lumped/finite element model[J]. Mechanical Systems and Signal Processing, 2007, 21(2): 735–760. DOI:10.1016/j.ymssp.2006.06.004 |
| [2] |
曹晓辉, 姜树李, 郭晨海, 等.
内燃机配气机构的动力学虚拟仿真研究[J]. 内燃机工程, 2009, 30(2): 65–68.
CAO Xiaohui, JIANG Shuli, GUO Chenhai, et al. Research on dummy simulation for dynamics of valve train system in internal combustion engine[J]. Chinese Internal Combustion Engine Engineering, 2009, 30(2): 65–68. (in Chinese) |
| [3] |
秦凤莲, 毕玉华, 申立中, 等.
柴油机配气机构动力学仿真及优化[J]. 拖拉机与农用运输车, 2010, 37(5): 71–73.
QIN Fenglian, BI Yuhua, SHEN Lizhong, et al. Simulation and optimization of valve train of diesel engine[J]. Tractor & Farm Transporter, 2010, 37(5): 71–73. (in Chinese) |
| [4] |
成晓北, 倪宏俊, 王宇业, 等.
柴油机配气机构动力学特性的仿真与试验[J]. 车用发动机, 2011(1): 70–74.
CHENG Xiaobei, NI Hongjun, WANG Yuye, et al. Simulation and experiment for valve train dynamic characteristic of diesel engine[J]. Vehicle Engine, 2011(1): 70–74. (in Chinese) |
| [5] | Wang K W. Vibration analysis of engine timing chain drives with camshaft torsional excitations[C]//Proceedings of the Noise & Vibration Conference & Exposition, May 1, 1991, Traverse City, Michigan, United States.[S.l.]:SAE International Technical Papers, 1991:911063. |
| [6] |
孙鋆强.
从动件运动规律对凸轮轴扭转变形及其振动的影响[J]. 机械设计, 2002, 19(1): 37–38.
SUN Junqiang. The influence on torsional deformation of cam shaft and its vibration affected by motion law of follower[J]. Journal of Machine Design, 2002, 19(1): 37–38. (in Chinese) |
| [7] |
谢黎明, 黎新齐.
凸轮机构主动件的运动与振动特性分析[J]. 机械传动, 2008, 32(3): 73–74.
XIE Liming, LI Xinqi. Motion and vibration analysis of the characters of cam mechanism[J]. Journal of Mechanical Transmission, 2008, 32(3): 73–74. (in Chinese) |
| [8] |
唐林虎, 曾贤虎.
高速凸轮驱动系统的振动分析及解决方法[J]. 组合机床与自动化加工技术, 2008(9): 10–12.
TANG Linhu, ZENG Xianhu. Analysis and solve method of vibration for the high-speed cam driving systems[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2008(9): 10–12. (in Chinese) |
| [9] |
王远, 张家玺, 朱会田, 等.
凸轮轴动力学及多轴疲劳分析研究[J]. 内燃机工程, 2010, 31(1): 104–107.
WANG Yuan, ZHANG Jiaxi, ZHU Huitian, et al. Study on dynamics and multi-axle fatigue analysis of camshaft[J]. Chinese Internal Combustion Engine Engineering, 2010, 31(1): 104–107. (in Chinese) |
| [10] | Saka Z, Yilmaz Y. Torsional vibrations of camshafts[J]. Mechanism and Machine Theory, 1992, 27(3): 225–233. DOI:10.1016/0094-114X(92)90012-7 |
| [11] | Teodorescu M, Kushwaha M, Rahnejat H, et al. Transient analysis of a line of valves with camshaft flexibility and valve-spring surge effects[C]//Proceedings of the ASME 2003 International Mechanical Engineering Congress and Exposition, November 15-21, 2003, Washington, DC, USA.[S.l.]:Design Engineering Division, 2003:1091-1097. |
| [12] | Guo J, Zhang W P, Zou D Q. Investigation of dynamic characteristics of a valve train system[J]. Mechanism and Machine Theory, 2011, 46(12): 1950–1969. DOI:10.1016/j.mechmachtheory.2011.07.014 |
| [13] | Teodorescu M, Kushwaha M, Rahnejat H, et al. Elastodynamic transient analysis of a four-cylinder valvetrain system with camshaft flexibility[J]. Journal of Multi-body Dynamic, 2005, 219(1): 13–25. |
| [14] | Mehrgou M. Study the effect of torsional vibration on valvetrain dynamic in a heavy duty diesel engine using multi-body dynamic[C]//Proceedings of the ASME 2009 Internal Combustion Engine Division Fall Technical Conference, September 27-30, 2009, Lucerne, Switzerland.[S.l.]:Internal Combustion Engine Division, 2009:507-511. |
| [15] | Guo J, Zhang W P, Cao Y P. Modeling and Simulation of Dynamic Behavior of Valve Train[C]//Proceedings of the 3rd Joint International Conference on Modelling and Simulation/3rd International Conference on Information and Computing Science, June 4-6, 2010, Wuxi, CHINA.[S.L.]:Procedia Engineering, 2010:241-246. |
| [16] |
覃文洁, 贺建强, 李志辉.
基于多体系统动力学的某V型发动机配气机构总成的动态仿真研究[J]. 北京理工大学学报, 2009, 29(10): 869–872.
QIN Wenjie, HE Jianqiang, LI Zhihui. A study on the simulation of valve train assembly of a v-type engine based on multi-body system dynamics[J]. Transactions of Beijing Institute of Technology, 2009, 29(10): 869–872. (in Chinese) |
 2013, Vol. 36
2013, Vol. 36

