子结构模态综合法是大型复杂结构动力学分析的一类有效方法,其中固定界面模态综合法通常具有较高的计算精度[1-3]。以往对其研究主要限于获得复杂结构的低阶模态,随着响应分析频率上升至结构中频段,对中高阶模态的精确综合逐渐成为研究的关键[4-7]。然而采用标准的固定界面模态综合法求解复杂结构中频段的振动响应效率不高,原因在于其模态综合过程中必须保留全部子结构低阶主模态。Shyu等[8-9]提出在坐标变换过程中引入准静力模态,实现了子结构低阶主模态截断。但这种方法中模态坐标下的系统动力学方程未能解耦,影响计算效率。笔者研究移频技术在子结构低阶主模态截断中的应用,对子结构动力学方程做移频处理,将子结构静力约束模态转换为准静力模态,同时实现了模态坐标下的系统动力学方程解耦。通过截断子结构低阶主模态,在保证系统中频段振动响应分析精度的前提下提高了计算效率,并以某白车身有限元模型为例验证该方法的有效性。
1 固定界面模态综合法及其计算效率分析 1.1 固定界面模态综合法固定界面模态综合方法的基本思想是将复杂模型划分为若干个子结构,分析子结构的动态特性,得到各子结构的主模态和约束模态。根据各子结构界面位移协调关系,得到系统模态坐标下的运动方程[10-12]。
为简化研究,忽略阻尼的影响,则子结构自由振动微分方程为
| $ \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{m}}_{ii}}}&{{\mathit{\boldsymbol{m}}_{ij}}}\\ {{\mathit{\boldsymbol{m}}_{ji}}}&{{\mathit{\boldsymbol{m}}_{jj}}} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\ddot X}}}_i}}\\ {{{\mathit{\boldsymbol{\ddot X}}}_j}} \end{array}} \right\} + \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{k}}_{ii}}}&{{\mathit{\boldsymbol{k}}_{ij}}}\\ {{\mathit{\boldsymbol{k}}_{ji}}}&{{\mathit{\boldsymbol{k}}_{jj}}} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{X}}_i}}\\ {{\mathit{\boldsymbol{X}}_j}} \end{array}} \right\} = \left\{ {\begin{array}{*{20}{c}} {\bf{0}}\\ {{\mathit{\boldsymbol{f}}_j}} \end{array}} \right\}, $ | (1) |
式中:下标i和j分别对应子结构内部自由度和界面自由度;m和k分别代表子结构质量矩阵和刚度矩阵,X为子结构物理坐标,fj为子结构界面上的相互作用力。
组集子结构的主模态和静力约束模态,得到子结构的坐标转换矩阵
| $ \mathit{\boldsymbol{W = }}\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{ir}}}&{{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_c}}\\ {\bf{0}}&\mathit{\boldsymbol{I}} \end{array}} \right], $ | (2) |
式中,子结构保留的前r阶主模态Φir=[φ1 φ2 … φr](r≪i),子结构静力约束模态Ψc=-kii-1kij,采用坐标转换矩阵W得子结构模态坐标下动力学方程
| $ \left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\tilde m}}}_{rr}}}&{{{\mathit{\boldsymbol{\tilde m}}}_{rj}}}\\ {{{\mathit{\boldsymbol{\tilde m}}}_{jr}}}&{{{\mathit{\boldsymbol{\tilde m}}}_{jj}}} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\ddot P}}}_r}}\\ {{{\mathit{\boldsymbol{\ddot P}}}_j}} \end{array}} \right\} + \left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\tilde k}}}_{rr}}}&{\bf{0}}\\ {\bf{0}}&{{{\mathit{\boldsymbol{\tilde k}}}_{jj}}} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{P}}_r}}\\ {{\mathit{\boldsymbol{P}}_j}} \end{array}} \right\} = \left\{ {\begin{array}{*{20}{c}} {\bf{0}}\\ {{\mathit{\boldsymbol{f}}_j}} \end{array}} \right\}, $ | (3) |
式中:下标r和j分别对应模态坐标下子结构内部自由度和界面自由度;
根据子结构间界面位移协调条件,组集系统模态坐标下的动力学方程
| $ \left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\tilde M}}}_{nn}}}&{{{\mathit{\boldsymbol{\tilde M}}}_{nc}}}\\ {{{\mathit{\boldsymbol{\tilde M}}}_{cn}}}&{{{\mathit{\boldsymbol{\tilde M}}}_{cc}}} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\ddot Q}}}_n}}\\ {{{\mathit{\boldsymbol{\ddot Q}}}_c}} \end{array}} \right\} + \left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\tilde K}}}_{nn}}}&{\bf{0}}\\ {\bf{0}}&{{{\mathit{\boldsymbol{\tilde K}}}_{cc}}} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{Q}}_n}}\\ {{\mathit{\boldsymbol{Q}}_c}} \end{array}} \right\} = \left\{ {\begin{array}{*{20}{c}} {\bf{0}}\\ {\bf{0}} \end{array}} \right\}, $ | (4) |
式中:下标n和c分别对应模态坐标下系统内部自由度和界面自由度;
固定界面模态综合法在求解复杂结构低频振动特性时,将子结构中、高阶主模态截断,节省了计算时间。若求解系统中频段动态特性时,能否将子结构低阶、高阶主模态截断,从而提高计算效率呢?下面对此进行分析。
将式(4)中系统的主模态进一步区分为保留的主模态和预截断的主模态
| $ \begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\tilde K}}_{nn}^{\rm{a}}}&{}&{}\\ {}&{\mathit{\boldsymbol{\tilde K}}_{nn}^{\rm{b}}}&{}\\ {}&{}&{{{\mathit{\boldsymbol{\tilde K}}}_{cc}}} \end{array}} \right]\left( {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{Q}}_n^{\rm{a}}}\\ {\mathit{\boldsymbol{Q}}_n^{\rm{b}}}\\ {{\mathit{\boldsymbol{Q}}_c}} \end{array}} \right) - }\\ {{\omega ^2}\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\tilde M}}_{nn}^{\rm{a}}}&{}&{\mathit{\boldsymbol{\tilde M}}_{nc}^{\rm{a}}}\\ {}&{\mathit{\boldsymbol{\tilde M}}_{nn}^{\rm{b}}}&{\mathit{\boldsymbol{\tilde M}}_{nc}^{\rm{b}}}\\ {\mathit{\boldsymbol{\tilde M}}_{cn}^{\rm{a}}}&{\mathit{\boldsymbol{\tilde M}}_{cn}^{\rm{b}}}&{{{\mathit{\boldsymbol{\tilde M}}}_{cc}}} \end{array}} \right]\left( {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{Q}}_n^{\rm{a}}}\\ {\mathit{\boldsymbol{Q}}_n^{\rm{b}}}\\ {{\mathit{\boldsymbol{Q}}_c}} \end{array}} \right) = \left\{ {\begin{array}{*{20}{c}} {\bf{0}}\\ {\bf{0}}\\ {\bf{0}} \end{array}} \right\},} \end{array} $ | (5) |
式中上标a和b分别对应系统保留的主模态和预截断的主模态。将方程的第2行展开,得系统预截断的主模态
| $ \mathit{\boldsymbol{Q}}_n^{\rm{b}} = \left[ {\frac{{{{\left( {\omega /{\omega ^{\rm{b}}}} \right)}^2}}}{{1 - {{\left( {\omega /{\omega ^{\rm{b}}}} \right)}^2}}}} \right]\mathit{\boldsymbol{\tilde M}}_{nc}^{\rm{b}}{\mathit{\boldsymbol{Q}}_c}, $ | (6) |
式中:
当ωb逐渐增大时;ω/ωb逐渐减小并趋近于0;
当ωb逐渐减小时,ωb/ω逐渐减小并趋近于0,
由以上分析可知,传统固定界面模态综合法中,由于界面模态的影响,在求解系统中频段模态时,子结构的高阶主模态可以舍弃,但低价主模态却不可截断。这就导致了系统中频段响应分析计算效率不高。
1.3 准静力模态法为了实现子结构低阶主模态截断,Shyu等[7-8]提出准静力模态法,即定义一个准静力模态
| $ {{\mathit{\boldsymbol{ \boldsymbol{\hat \varPsi} }}}_c} = - {\left( {{\mathit{\boldsymbol{k}}_{ii}} - \omega _0^2{\mathit{\boldsymbol{m}}_{ii}}} \right)^{ - 1}}\left( {{\mathit{\boldsymbol{k}}_{ij}} - \omega _0^2{\mathit{\boldsymbol{m}}_{ij}}} \right)。$ | (7) |
相比静力约束模态,准静力模态包含了系统在关心频率ω0附近的惯性力影响因素,使得子结构的低阶主模态在组集系统ω0附近的中频段模态时重要性下降,从而保证了舍弃子结构低阶主模态时仍然准确表达系统中频段模态的能力。
采用准静力模态后,子结构模态坐标下的刚度矩阵为
| $ \mathit{\boldsymbol{\hat k = }}{{\mathit{\boldsymbol{\hat W}}}^{\rm{T}}} \cdot \mathit{\boldsymbol{k}} \cdot \mathit{\boldsymbol{\hat W}} = \left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\hat k}}}_{rr}}}&{{{\mathit{\boldsymbol{\hat k}}}_{rj}}}\\ {{{\mathit{\boldsymbol{\hat k}}}_{jr}}}&{{{\mathit{\boldsymbol{\hat k}}}_{jj}}} \end{array}} \right], $ | (8) |
式中:坐标变换矩阵
由于非零矩阵
综上所述,不论是传统的固定界面模态综合法还是准静力模态法,在分析系统中频段模态时都存在计算效率不高的问题,有必要研究适用于复杂结构中频段动态响应分析的方法。
2 基于移频技术的主模态截断方法移频是振动分析中的一种重要技术,即在动力学方程中将结构固有频率按某一定值向原点方向移动,加快特征值求解过程迭代收敛速度,同时方便得到结构中频段固有频率[13-14]。
将移频技术引入固定界面模态综合法中,取系统关心频段内一点(常取频段中点)为中心频率ω0,对结构原固有频率ω作移频处理,得移频后的固有频率
| $ {{\bar \omega }^2} = {\omega ^2} - \omega _0^2。$ | (9) |
由此得到移频处理后的子结构自由振动微分方程
| $ \left[ {\left( {\mathit{\boldsymbol{k}} - \omega _0^2\mathit{\boldsymbol{m}}} \right) - {{\bar \omega }^2}\mathit{\boldsymbol{m}}} \right]\mathit{\boldsymbol{X = }}\left[ {\mathit{\boldsymbol{\bar k}} - {{\bar \omega }^2}\mathit{\boldsymbol{m}}} \right]\mathit{\boldsymbol{X}} = 0。$ | (10) |
与式(1)相比,移频后子结构的质量矩阵m保持不变,而刚度矩阵由k变为k,即
| $ \mathit{\boldsymbol{\bar k}} = \left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\bar k}}}_{ii}}}&{{{\mathit{\boldsymbol{\bar k}}}_{ij}}}\\ {{{\mathit{\boldsymbol{\bar k}}}_{ji}}}&{{{\mathit{\boldsymbol{\bar k}}}_{jj}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{k}}_{ii}} - \omega _0^2{\mathit{\boldsymbol{m}}_{ii}}}&{{\mathit{\boldsymbol{k}}_{ij}} - \omega _0^2{\mathit{\boldsymbol{m}}_{ij}}}\\ {{\mathit{\boldsymbol{k}}_{ji}} - \omega _0^2{\mathit{\boldsymbol{m}}_{ji}}}&{{\mathit{\boldsymbol{k}}_{jj}} - \omega _0^2{\mathit{\boldsymbol{m}}_{jj}}} \end{array}} \right]。$ | (11) |
由此得到移频后子结构的静力约束模态
| $ {{\mathit{\boldsymbol{ \boldsymbol{\varPsi} '}}}_c} = - {\left( {{\mathit{\boldsymbol{k}}_{ii}} - \omega _0^2{\mathit{\boldsymbol{m}}_{ii}}} \right)^{ - 1}}\left( {{\mathit{\boldsymbol{k}}_{ij}} - \omega _0^2{\mathit{\boldsymbol{m}}_{ij}}} \right)。$ | (12) |
Ψ′c与式(7)中准静力模态表述一样,同样包含了系统惯性力影响因素,因此也能保证截断子结构低阶主模态时仍然准确表达系统中频段模态的能力。
组集子结构坐标转换矩阵W′,对子结构进行坐标变换,得子结构刚度矩阵为
| $ \mathit{\boldsymbol{k'}} = {{\mathit{\boldsymbol{W'}}}^{\rm{T}}} \cdot \mathit{\boldsymbol{\bar k}} \cdot \mathit{\boldsymbol{W' = }}\left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{k'}}}_{rr}}}&{{{\mathit{\boldsymbol{k'}}}_{rj}}}\\ {{{\mathit{\boldsymbol{k'}}}_{jr}}}&{{{\mathit{\boldsymbol{k'}}}_{jj}}} \end{array}} \right], $ | (13) |
式中:k′rj=Φir·(kii-ω02mii)·Ψ′cT+Φir·(kij-ω02mij)=0,k′jr =k′rjT=0。表明移频处理后子结构模态坐标下的刚度矩阵实现了解耦,弥补了准静力模态法因刚度矩阵未能解耦影响计算效率的缺陷。
为进一步分析子结构主模态与系统中频段模态的关系,组建移频后的系统模态坐标下动力学方程为
| $ \begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\bar K}}_{nn}^{\rm{a}}}&{}&{}\\ {}&{\mathit{\boldsymbol{\bar K}}_{nn}^{\rm{b}}}&{}\\ {}&{}&{{{\mathit{\boldsymbol{\bar K}}}_{cc}}} \end{array}} \right]\left( {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\bar Q}}_n^{\rm{a}}}\\ {\mathit{\boldsymbol{\bar Q}}_n^{\rm{b}}}\\ {{{\mathit{\boldsymbol{\bar Q}}}_c}} \end{array}} \right) - }\\ {{{\bar \omega }^2}\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\bar M}}_{nn}^{\rm{a}}}&{}&{\mathit{\boldsymbol{\bar M}}_{nc}^{\rm{a}}}\\ {}&{\mathit{\boldsymbol{\bar M}}_{nn}^{\rm{b}}}&{\mathit{\boldsymbol{\bar M}}_{nc}^{\rm{b}}}\\ {\mathit{\boldsymbol{\bar M}}_{cn}^{\rm{a}}}&{\mathit{\boldsymbol{\bar M}}_{cn}^{\rm{b}}}&{{{\mathit{\boldsymbol{\bar M}}}_{cc}}} \end{array}} \right]\left( {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\bar Q}}_n^{\rm{a}}}\\ {\mathit{\boldsymbol{\bar Q}}_n^{\rm{b}}}\\ {{{\mathit{\boldsymbol{\bar Q}}}_c}} \end{array}} \right) = \left\{ {\begin{array}{*{20}{c}} {\bf{0}}\\ {\bf{0}}\\ {\bf{0}} \end{array}} \right\},} \end{array} $ | (14) |
对比式(5)可得,移频处理前后系统动力学方程中刚度矩阵均实现了解耦,说明引入移频技术没有额外增加系统动力学方程的计算量。将方程的第2行展开,可得系统预截断主模态
| $ \mathit{\boldsymbol{\bar Q}}_n^{\rm{b}} = \left[ {\frac{{{{\left( {\bar \omega /{{\bar \omega }^{\rm{b}}}} \right)}^2}}}{{1 - {{\left( {\bar \omega /{{\bar \omega }^{\rm{b}}}} \right)}^2}}}} \right]\mathit{\boldsymbol{\bar M}}_{nc}^{\rm{b}}{{\mathit{\boldsymbol{\bar Q}}}_c}。$ | (15) |
根据式(9)有(ωb)2=(ωb)2-ω02,代入式(15)中得
| $ \mathit{\boldsymbol{\bar Q}}_n^{\rm{b}} = \frac{{{\omega ^2} - \omega _0^2}}{{{{\left( {{\omega ^{\rm{b}}}} \right)}^2} - {\omega ^2}}}\mathit{\boldsymbol{\bar M}}_{nc}^{\rm{b}}{{\mathit{\boldsymbol{\bar Q}}}_c}, $ | (16) |
式中ωb代表预截断的主模态固有频率。
当ωb逐渐增大时,ω/ωb逐渐减少并趋近于0,ω0/ωb逐渐减小并趋近于0,
当ωb逐渐减小,且关心频率段为一中频段窄带(ω足够大,ω0接近ω)时,
由此可得:在模态综合过程中引入移频技术,当关心频段为中频段窄带时,子结构高阶主模态和低阶主模态都可以适当截断,只保留关心频段附近足够带宽的中频段主模态,就能保证动态响应分析精度,同时减少系统动力学方程自由度,提高计算效率。
3 实例验证分析某白车身有限元模型(图 1)中频段的动态响应特性。设定单元尺寸为20 mm左右,得到网格总数为138 084个,其中四边形单元117 557个,三角形单元14 985个,并通过5 542个梁单元模拟车身焊点。材料密度ρ=7.85×10-3g/mm3,杨氏弹性模量E=2.1×106 MPa,泊松比μ=0.28。

|
图 1 白车身有限元模型 |
在发动机右端悬置点处施加Z方向的谐响应激励,以160 Hz至190 Hz频率段作为关心频段,取中心频率为175 Hz,基于NASTRAN软件平台,将白车身划分为32个子结构,分别运用结合移频技术的模态综合法(以下称移频算法)和传统模态综合法(以下称标准算法),分析两种算法所得白车身关心频段内的固有频率,并比较驾驶员位置处Z方向的加速度响应。
结构响应分析模态截断准则中,通常须保证系统模态截断频率为响应分析频段上限的两倍以上,同时子结构主模态截断频率为系统模态截断频率的两倍以上[15]。因此采用标准算法时分别取系统模态截断频率为400 Hz,子结构主模态截断频率为800 Hz,以保证系统在190 Hz以内的动态响应分析的准确度。采用移频算法时,根据中心频率(175 Hz)以及关心频段宽度,选取系统模态频段上下限为130 Hz和220 Hz,选取子结构主模态频段上下限为85 Hz和265 Hz。
分别用标准算法和移频算法计算白车身在关心频段内的固有频率f1、f2,并得到f2相对f1的计算误差(表 1)。
| 表 1 两种算法所得系统固有频率 |
由表 1可以看到,两种算法所得系统固有频率结果总体呈现离中心频率越远相对误差越大的趋势,整个目标频段内相对误差不超过0.21%。说明基于移频技术的固定界面模态综合法保持了较高的计算精度。
两种算法在模态综合过程中部分子结构保留的主模态数量如表 2所示。
| 表 2 两种算法保留的子结构主模态数量 |
由表 2可以看到,移频算法在模态综合过程中各个子结构保留的主模态数量相比标准算法明显下降,标准算法中系统共需保留1 836阶主模态,而移频算法仅使用297阶主模态,大幅减少了模态坐标下的系统动力学方程自由度。
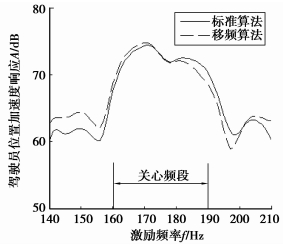
分析驾驶员位置处某点Z方向加速度响应A,得两种算法下驾驶员位置加速度响应幅值(图 2)和响应相对误差(图 3)。
|
图 2 两种方法所得加速度响应 |
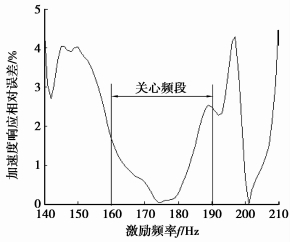
|
图 3 移频后加速度响应相对误差 |
由图 2可以看到,两种算法所得的驾驶员处加速度响应曲线在160 Hz至190 Hz的关心频段内基本吻合。由图 3可以看到,相对于标准算法,移频算法所得加速度幅值的计算误差在整个关心频段内小于3%。说明采用移频算法分析系统中频段动态响应具有较高精度。
上述计算在CPU为Core i5,主频为2.80 GHz,内存8 GB的四核计算机上进行。
标准算法分析系统中频段加速度响应耗时1 779 s,而移频算法仅需1 287 s,减少分析时间27.7%。说明移频处理后系统中频段动态响应分析效率显著提高。
5 结论笔者研究了固定界面模态综合法在求解结构中频段响应时计算效率的改进方法。通过在模态综合的过程中引入移频技术,实现了子结构低阶主模态截断,提高了计算效率。对白车身实例分析结果表明,在保证计算精度的前提下,该方法所需的子结构主模态数量相比标准固定界面模态综合法大幅减少,从而节省分析时间27.7%。这里仅将移频技术应用于子结构低阶主模态截断上,对于低阶界面模态的截断还有待研究,以期进一步提高模态综合法应用于中频段响应分析时的计算效率。
| [1] | Tran D M. Component mode synthesis methods using partial interface modes:application to tuned and mistuned structures with cyclic symmetry[J]. Computer & Structures, 2009, 87(17/18): 1141–1153. |
| [2] | Jakobsson H, Larson M G. A posteriori error analysis of component mode synthesis for the elliptic eigenvalue problem[J]. Computer Methods Applied Mechanics and Engineering, 2011, 200(41/42/43/44): 2840–2847. |
| [3] | Hinke L, Dohnal F, Mace B R, et al. Component mode synthesis as a framework for uncertainty analysis[J]. Journal of Sound and Vibration, 2009, 324(1/2): 161–178. |
| [4] |
应祖光, 叶淑琴, 金林.
基于固定界面子结构模态的频响函数精确综合法[J]. 振动与冲击, 2010, 29(3): 132–133.
YING Zuguang, YE Shuqin, JIN Lin. Exact frequency-response-function synthesis method using interface-fixed substructure modes[J]. Journal of Vibration and Shock, 2010, 29(3): 132–133. (in Chinese) |
| [5] |
叶淑琴, 应祖光.
中高阶子结构模态的精确综合法[J]. 工程力学, 2009, 26(Sup Ⅰ): 20–23.
YE Shuqin, YING Zuguang. Exact modal synthesis method using mid/high-order substructure modes[J]. Engineering Mechanics, 2009, 26(Sup Ⅰ): 20–23. (in Chinese) |
| [6] | Ji L, Mace B R, Pinnington R J. A mode-based approach for the mid-frequency vibration analysis of coupled long-and short-wavelength structures[J]. Journal of Sound and Vibration, 2006, 289(1/2): 148–170. |
| [7] | Sarkar A, Ghanem R. A substructure approach for the midfrequency vibration of stochastic systems[J]. Journal of the Acoustical Society of America, 2003, 113(4): 1922–1934. DOI:10.1121/1.1558374 |
| [8] | Shyu W H, Ma Z D, Hulbert G M. A new component mode synthesis method:quasi-static mode compensation[J]. Finite Elements in Analysis and Design, 1997, 24(4): 271–281. DOI:10.1016/S0168-874X(96)00066-2 |
| [9] | Shyu W H, Gu J M, Hulbert G M, et al. On the use of multiple quasi-static mode compensation sets for component mode synthesis of complex structures[J]. Finite Elements in Analysis and Design, 2000, 35(2): 119–140. DOI:10.1016/S0168-874X(99)00058-X |
| [10] |
钱志英, 罗文波, 阮剑华.
MSC.NASTRA子结构法在航天器结构动力学分析中的应用[J]. 航天器工程, 2011, 20(5): 55–60.
QIAN Zhiying, LUO Wenbo, RUAN Jianhua. Application of substructure method based on MSC.NASTRAN in spacecraft structural analysis[J]. Spacecraft Engineering, 2011, 20(5): 55–60. (in Chinese) |
| [11] |
杜飞平, 谭永华, 陈建华, 等.
航天器子结构模态综合法研究现状及进展[J]. 火箭推进, 2010, 36(3): 39–44, 62.
DU Feiping, TAN Yonghua, CHEN Jianhua, et al. Status and progress on substructual modal synthesis techniques for space vehicles[J]. Journal of Rocket Propulsion, 2010, 36(3): 39–44, 62. (in Chinese) |
| [12] | Park K. Component-based vibration modeling methods for fast reanalysis and design of complex structures[D]. Michigan: University of Michigan, 2008. |
| [13] |
张安平, 陈国平.
一种新的有限元模型移频动力缩聚法[J]. 计算力学学报, 2011, 28(2): 168–172, 295.
ZHANG Anping, CHEN Guoping. A novel dynamic condensation method with shift for finite element models[J]. Chinese Journal of Computational Mechanics, 2011, 28(2): 168–172, 295. DOI:10.7511/jslx201102002 (in Chinese) |
| [14] | Zhao Q C, Chen P, Peng W B, et al. Accelerated subspace iteration with aggressive shift[J]. Computers & Structures, 2007, 85(19/20): 1562–1578. |
| [15] |
姜忻良, 王菲.
基于势能判据的约束模态综合法截断准则[J]. 振动与冲击, 2011, 30(2): 32–38.
JIANG Xinliang, WANG Fei. Mode cut-off criterion of constrained mode synthesis method based on a potential energy criterion[J]. Journal of Vibration and Shock, 2011, 30(2): 32–38. (in Chinese) |
 2013, Vol. 36
2013, Vol. 36


