b. 北京航空航天大学 机械学院, 北京 100191
b. School of Mechanical Engineering, Beijing University of Aeronautics & Astronautics, Beijing 100191, China
谐波传动广泛应用于航空航天、数控机床和各种自动控制系统等领域。谐波传动由于采用了柔轮结构使其能够获得速比大和结构紧凑等一系列其他传动形式无法取代的优点,也正是因为柔轮特性使得谐波传动存在传动刚度差、近似啮合传动质量不理想及轴向尺寸略大等问题;同时由于柔轮材料强度的限制,谐波传动单级传动比下限在80左右,而传动比在18至60范围的减速需求量占68%,因此降低单级传动比以及如何提高谐波传动性能方面的研究大多围绕柔轮进行,如改善齿廓曲线,提高啮合质量。
离散齿谐波传动是对谐波传动结构的改进和扩展:用离散齿轮代替柔轮,解决采用柔轮带来的刚度问题;刚轮曲线不是渐开线而是按等速共轭原理设计的离散齿包络线,并且啮合齿数多,解决了谐波传动精度问题;离散齿谐波传动比的范围可在12至80范围内,这是谐波传动不能达到的,以满足实际应用的需求。因此,对离散齿谐波传动的研究极具理论价值和应用前景[1-3]。
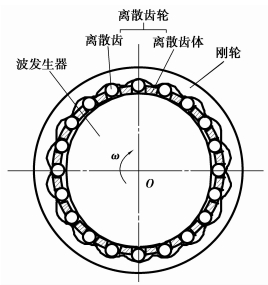
1 离散齿谐波传动结构离散齿谐波传动由离散齿轮、刚轮和波发生器3个基本构件组成,图 1为离散齿谐波传动结构简图。
|
图 1 离散齿谐波传动结构简图 |
其中,波发生器与谐波传动相同,由一个双波或多波的凸轮外套一薄壁轴承组成,以椭圆凸轮最为常用;离散齿轮是由一个开有若干径向槽的圆环和置于槽中的一组中间可动件——离散齿组成,离散齿可以是球形、圆柱形或两侧做成平面的圆柱体,以圆柱形较好,齿槽则与离散齿相匹配;刚轮与谐波传动类似,为一刚性厚环,环内壁开有轮齿。刚轮齿廓曲线不是渐开线而是按等速共轭原理设计的离散齿包络线,即选定离散齿形状后,在椭圆凸轮波发生器驱动下,用等速共轭原理计算出离散齿的包络线,即刚轮的齿廓曲线。运动传递是在波发生器的作用下,使离散齿运动,与刚轮、离散齿体互相作用实现传动。不同的输入输出构件、波发生器波数以及刚轮齿廓工作区间等,可以得到多种不同的离散齿传动方案,设计者根据使用需求进行选择。
2 离散齿啮合副受力分析与计算离散齿谐波传动是过约束机构,受力复杂,在分析受力时需要考虑变形协调方程。以椭圆凸轮波发生器、圆柱形离散齿为例,对离散齿谐波传动进行受力分析,令波发生器作为输入构件,离散齿体作为输出构件,刚轮固定。椭圆凸轮波发生器中心对称,运动时,处于啮合状态的离散齿位于相对转动轴中心对称的两个区域内,且两啮合区内相应的离散齿受力等值反向。为了减少计算量,只计算其中一个啮合区内离散齿的受力[4-5]。
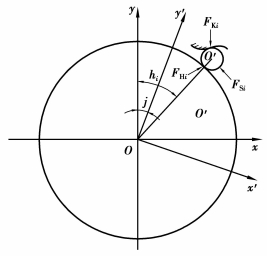
图 2为离散齿受力图。xoy为固定坐标系;x′oy′为波发生器的连体坐标系,x′轴对应波发生器的短半轴,y′轴对应波发生器的长半轴。假设波发生器的输入角j=0为运动的起始位置,令与波发生器长半轴接触的离散齿标号为0,顺时针依次递推,第i个离散齿中心与y轴的夹角为hi。
|
图 2 单个离散齿受力图 |
离散齿受波发生器、离散齿体和刚轮三方面的作用力。离散齿谐波传动的传动效率高:其共轭齿廓间的运动不是纯滑动的,而是滚动或者滚动带有滑动;啮合零部件的表面加工质量要求高,摩擦系数小。摩擦力对整个结构受力状态的影响很小,在计算时,忽略相互接触物体间的摩擦。略去物体本身的重力以及物体运动所受的惯性力,离散齿的受力平衡方程为[6-7]。
| $ \left\{ \begin{array}{l} {F_{{\rm{H}}i}}\;{\rm{cos}}\;{\theta _{{\rm{H}}i}} + {F_{{\rm{K}}i}}\;{\rm{cos}}\;{\theta _{{\rm{K}}i}} + {F_{{\rm{S}}i}}\;{\rm{cos}}\;{\theta _{{\rm{S}}i}} = 0,\\ {F_{{\rm{H}}i}}\;{\rm{sin}}\;{\theta _{{\rm{H}}i}} + {F_{{\rm{K}}i}}\;{\rm{sin}}\;{\theta _{{\rm{K}}i}} + {F_{{\rm{S}}i}}\;{\rm{sin}}\;{\theta _{{\rm{S}}i}} = 0。\end{array} \right. $ | (1) |
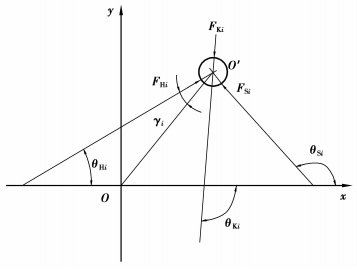
式中:FHi、FKi、FSi分别为波发生器、刚轮和离散齿体对离散齿的法向作用力;θHi、θKi、θSi(图 3)为3个作用力方向与x轴的夹角,是离散齿传动结构尺寸和运动位置的函数,可由几何参数计算。
|
图 3 离散齿受力与作用角 |
图 3离散齿受力与作用角设输入力矩为M0,每个啮合区内啮合齿数为n。由于FHi的反作用力F′Hi对转动轴的力矩之和等于作用在波发生器上的输入力矩M0,两个啮合区域具有对称性,则力矩平衡方程为
| $ {M_0} = 2\sum\limits_{i = 1}^n {F{\prime _{{\rm{H}}i}}} \left| {{\mathit{\boldsymbol{d}}_i}} \right|\;{\rm{sin }}{\gamma _i}。$ | (2) |
式中di表示离散齿中心到旋转轴的距离。
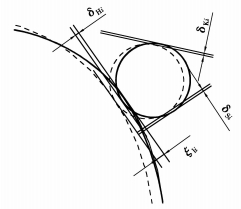
2.2 变形协调方程每个离散齿的3个啮合点处会产生接触变形,3个接触变形共同作用导致波发生器旋转一个很小的角度Δφi。在离散齿与波发生器的接触点,由于3个接触变形量导致该点沿FHi方向的位移ξ1i等于波发生器旋转一个微角度,该点沿FHi方向的位移为
| $ \begin{array}{l} {\xi _{1i}} = {\delta _{{\rm{H}}i}} + {\delta _{{\rm{K}}i}}\;{\rm{cos}}\;(\pi + {\theta _{{\rm{K}}i}} - {\theta _{{\rm{H}}i}}) + \\ \quad \quad {\delta _{{\rm{S}}i}}\;{\rm{cos}}\;(\pi /2 - {\gamma _i}), \end{array} $ | (3) |
| $ {\xi _{2i}} = \Delta {\varphi _i}\left| {{\mathit{\boldsymbol{d}}_i}} \right|\;{\rm{sin}}\;{\gamma _i}, $ | (4) |
| $ {\xi _{1i}} = {\xi _{2i}}, $ | (5) |
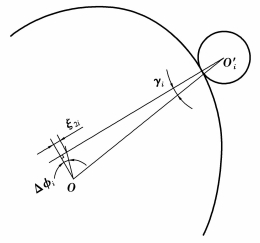
式中:δHi、δKi、δSi分别为离散齿与波发生器、刚轮和离散齿体的法向接触变形量;i=1, 2,…,n。图 4、5分别为ξ1i与ξ2i的示意图。
|
图 4 ξ1i的示意图 |
|
图 5 ξ2i的示意图 |
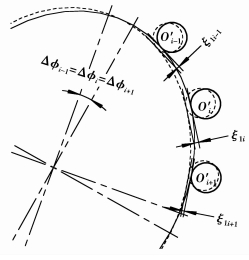
根据变形协调条件[8],在某瞬时,处于啮合状态的各离散齿其接触变形导致波发生器旋转的微小角度是相同的Δφi=Δφi+1(i=1, 2,…,n-1),如图 6,带入式(3)、(4)、(5)可得同一啮合瞬时处于啮合状态的相邻两个离散齿的变形协调关系。
| $ \begin{array}{c} \frac{{\left| {{\mathit{\boldsymbol{d}}_i}} \right|{\rm{sin}}{\gamma _i}}}{{\left| {{\mathit{\boldsymbol{d}}_i}_{i + 1}} \right|{\rm{sin}}{\gamma _{i + 1}}}} = \\ \frac{{{\delta _{{\rm{H}}i}} + {\delta _{{\rm{K}}i}}{\rm{cos}}(\pi + {\theta _{{\rm{K}}i}} - {\theta _{{\rm{H}}i}}) + {\delta _{{\rm{S}}i}}{\rm{cos}}(\pi /2 - {\gamma _i})}}{{{\delta _{{\rm{H}}i + 1}} + {\delta _{{\rm{K}}i + 1}}{\rm{cos}}(\pi + {\theta _{{\rm{K}}i + 1}} - {\theta _{{\rm{H}}i + 1}}) + {\delta _{{\rm{S}}i + 1}}{\rm{cos}}(\pi /2 - {\gamma _{i + 1}})}},\\ \left( {i = 1,2, \ldots ,n - 1} \right) \end{array} $ | (6) |
|
图 6 啮合离散齿间变形协调关系 |
由力与弹性变形关系知[9-10],3处啮合副作用力与接触变形的关系为
| $ \left\{ \begin{array}{l} {F_{{\rm{H}}i}} = {k_{\rm{H}}}{\delta _{Hi}},\\ {F_{{\rm{K}}i}} = {k_{\rm{K}}}{\delta _{{\rm{Ki}}}},\\ {F_{{\rm{S}}i}} = {k_{\rm{S}}}{\delta _{{\rm{S}}i}}。\end{array} \right. $ | (7) |
某一啮合瞬时,处于啮合状态的所有离散齿的受力可由式(7)求出,每个离散齿受三方面作用力,有n个齿啮合,共3n个未知数。由受力平衡方程(1)可以确定2n个方程;由力矩平衡方程(2)可确定一个方程;由变形协调方程(6)可确定n-1个方程,共3n个方程。未知数与方程数相等,可求出波发生器某输入角下处于啮合状态的所有离散齿受力。
3 啮合处接触应力的计算计算离散齿与刚轮、波发生器和离散齿体的接触应力时,将3处啮合副看成轴线平行的两圆柱体接触。由赫兹公式可知
| $ \sigma = \sqrt {\frac{F}{{\pi {L_1}}}\cdot\frac{{\frac{1}{{{\rho _1}}} + \frac{1}{{{\rho _2}}}}}{{\frac{{1 - \mu _1^2}}{{{E_1}}} + \frac{{1 - \mu _2^2}}{{{E_2}}}}}} , $ | (8) |
式中:F分别代表FHi、FKi、FSi、ρ1、ρ2通过离散齿的结构参数计算。
4 作用力和接触应力分布运用上述受力分析方法[11-12],可以求出波发生器某输入角下处于啮合状态的所有离散齿受力。通过取大量的j值,即可得到作用力沿波发生器、离散齿体和刚轮的分布。
在椭圆凸轮波发生器离散齿传动过程中,单个离散齿从进入到退出啮合需要波发生器转过π/2(刚轮齿廓未发生顶切),由于在这个过程中不断会有其他离散齿进入退出啮合,每个离散齿的受力是所有处于啮合状态离散齿共同作用的结果,因此在这种情况下建立方程组求受力分布很繁琐。现采用另外一种方法,即波发生器每转过2π/ZK(ZK是刚轮齿数),齿顶处有一个离散齿进入啮合,齿根处另一个离散齿退出啮合,将这个过程每个处于啮合状态的离散齿作为单个离散齿进入退出啮合过程的一部分进行组合,进而使之能够表达单个离散齿从进入到退出啮合作用力在接触面上的分布。
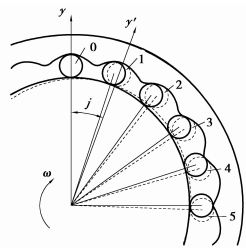
如图 7所示,实线表示周期起始时各离散齿的位置,虚线表示波发生器转过2π/ZK后各离散齿的位置。
|
图 7 波发生器转过2π/ZK前后各离散齿位置示意图 |
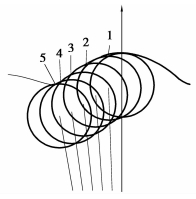
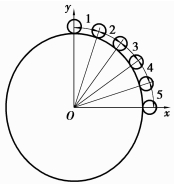
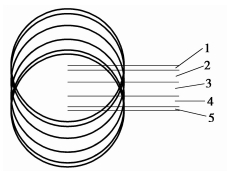
当波发生器转过2π/ZK,离散齿带动离散齿体旋转2π/(ZK×iHGK)(iHGK为传动比)。由图 7知,离散齿1转过2π/(ZK×iHGK)即离散齿2周期起始时的位置,离散齿2转过2π/(ZK×iHGK)即离散齿3周期起始的位置,以此类推。处于啮合状态的每个离散齿都可以表示单个离散齿从进入到退出啮合过程中的一部分,组合到一起即为单个离散齿由进入到退出啮合的过程。如图(8)、(9)、(10)所示,图上的数字1、2、3、4、5表示波发生器旋转2π/ZK相应标号的离散齿在各自刚轮、波发生器和离散齿轮的运动路径,以5、4、3、2、1的顺序进行组合为一个离散齿由进入到退出啮合的运动路径。在此基础上将输入角2π/ZK进行等分N,计算处于啮合状态的n个离散齿在这N+1个输入点的受力,将这n段受力值进行叠加即可。
|
图 8 各离散齿的运动路径在刚轮上的叠加 |
|
图 9 各离散齿运动路径在波发生器上的叠加 |
|
图 10 各离散齿的运动路径在离散齿体上的叠加 |
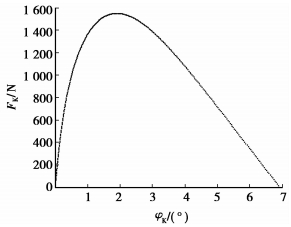
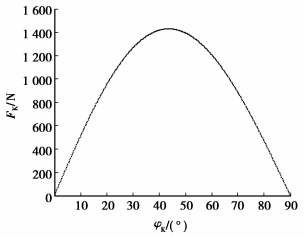
已知一离散齿谐波传动机构,运动由波发生器输入,离散齿体输出,刚轮固定。传动主要结构参数为波发生器长半轴和短半轴分别为a=58 mm、b=56 mm,离散齿半径r=5 mm,离散齿宽度L1=15 mm,离散齿齿数ZG=28,刚轮齿数ZK=26;假设弹性模量E=210 GPa,泊松比μ=0.3;输入力矩M0=20 N·m。此时,刚轮齿廓未发生顶切,传动重合度为ZG/2,离散齿啮合数量保持不变。取波发生器旋转j=2π/ZK过程中的50个等距点进行计算,得到50×7组FHi、FKi、FSi和σHi、σKi、σSi值,并使之与其啮合位置对应,计算结果如图 11~18所示。φK表示离散齿和刚轮的啮合点与刚轮齿顶相对于旋转轴的夹角;φH表示离散齿和波发生器的啮合点与波发生器短半轴相对于旋转轴的夹角。
|
图 11 FK在刚轮齿廓上的分布 |
|
图 12 FH在波发生器上的分布 |
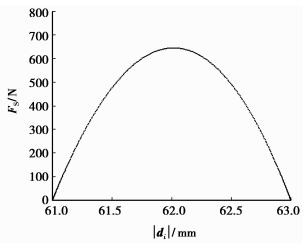
|
图 13 FS在离散齿体上的分布 |
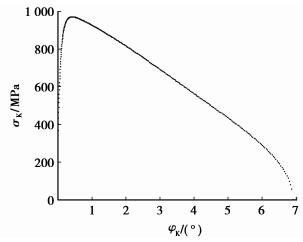
|
图 14 σK在刚轮齿廓上的分布 |
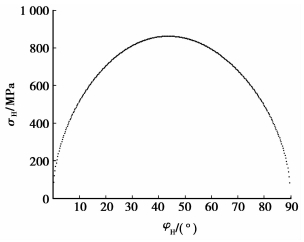
|
图 15 σH在波发生器上的分布 |
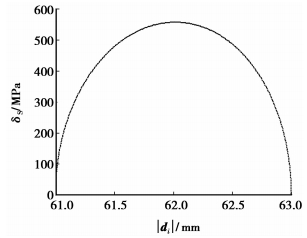
|
图 16 σS在离散齿体上的分布 |
|
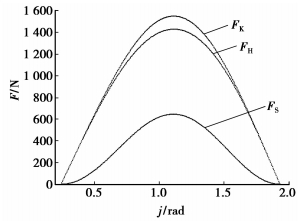
图 17 3个作用力随波发生器转角的变化 |
|
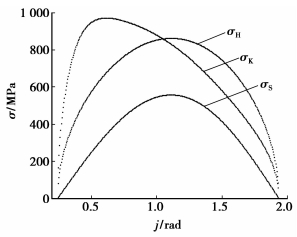
图 18 3个接触应力随波发生器转角的变化 |
图 11~16为作用力与接触应力在各接触面的分布;图 17和18为作用力与接触应力随波发生器转角的变化。可知离散齿从进入到退出啮合,受波发生器、刚轮和离散齿体的作用力以及接触应力表现出从零开始由小变大再变小至零的变化趋势,使传动过程平稳。在刚轮靠近齿顶的部分呈现出接触应力高,承载能力差的特点,对此可以进行齿廓修形改善受力分布,提高承载能力。
5.2 刚轮齿廓发生顶切的受力分析离散齿运动由波发生器输入,离散齿体输出,刚轮固定。传动主要结构参数:波发生器长半轴和短半轴分别为a=50.7 mm、b=49.3 mm,离散齿半径r=1.5 mm,离散齿宽度L1=15 mm,离散齿理论齿数ZG=80,做抽齿处理后实际齿数Z′G=40,刚轮齿数ZK=78;弹性模量E=210 GPa,泊松比μ=0.3;输入力矩为M0=3 N·m。
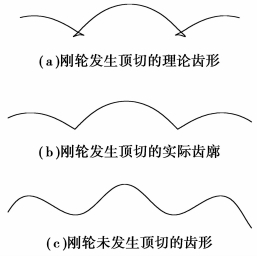
上述结构参数下,刚轮齿廓发生顶切,如图 19(b),因此在分析离散齿传动受力时,需计算传动重合度,将传动过程按参与啮合的离散齿数量分别计算,再进行整合,即可得到整个过程的啮合力变化情况。
|
图 19 刚轮齿廓发生与未发生顶切形状 |
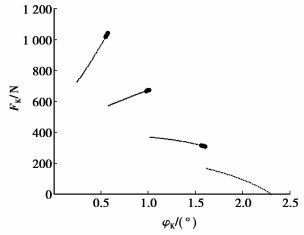
根据重合度的计算[17]得到上述参数下重合度ε=7.573 2。对于双波波发生器,同时啮合的离散齿齿数必为偶数,且相对于旋转轴中心对称,因此本例中处于啮合状态的离散齿齿数为6或8:以j=0作为运动的起始位置,以2π/ZK为周期,运动开始为6齿啮合,当波发生器旋转到一定角度,变为8齿啮合。由于啮合区域具有对称性,只需计算其中一个啮合区域(3齿与4齿的啮合)。计算同样取50个点,计算结果见图 20~25。
|
图 20 FK在刚轮齿廓上的分布 (刚轮齿廓发生顶切) |
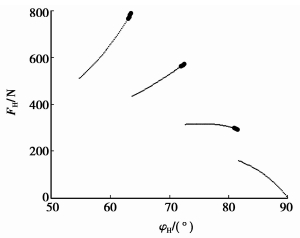
|
图 21 FH在波发生器上的分布 (刚轮齿廓发生顶切) |
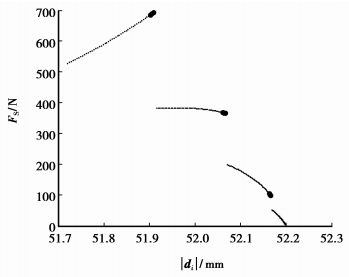
|
图 22 FS在离散齿体上的分布 (刚轮齿廓发生顶切) |
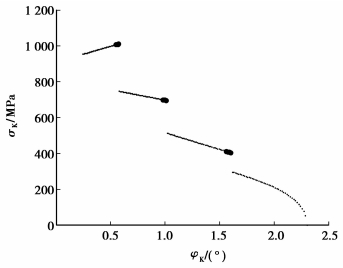
|
图 23 σK在刚轮齿廓上的分布 (刚轮齿廓发生顶切) |
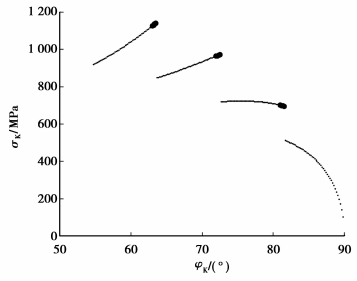
|
图 24 σH在波发生器上的分布 (刚轮齿廓发生顶切) |
|
图 25 σS在离散齿体上的分布 (刚轮齿廓发生顶切) |
图 20~25即为离散齿从齿顶进入啮合到齿根退出啮合过程的受力计算结果,假设此离散齿用A表示。当离散齿A刚进入啮合在齿顶附近,传动为4齿啮合,离散齿A的受力为图 20~25中第1段细点部分,其受力不是从零开始,而是相对较大的一个值。随着波发生器的转动,另一处在啮合状态并在齿根附近的离散齿D退出啮合,其受力是逐渐减小到零至退出的,因此其他离散齿的受力状态不会突变,离散齿A的受力如图 20~25第1段粗点到细点的过程,此时为3齿啮合。波发生器继续转动,在某一时刻,齿顶处会有新的离散齿E参加啮合,离散齿E所受作用力不是从零开始,因此其他3个离散齿的受力会发生突变,离散齿A的受力如图 20~25第1段粗点到第2段细点的过程,此时为4齿啮合。随着波发生器继续转动,在齿根处会有离散齿退出啮合,齿顶处会有离散齿进入啮合,如此循环下去,直到离散齿A运动到齿根退出啮合,其受力及接触应力可由图 20~25表述。
由结果可以看出,由于刚轮齿廓发生顶切,导致同时啮合齿数减少,使得每个离散齿的负担增加;刚进入啮合的离散齿受力情况恶劣,接触应力高;当齿顶处的离散齿进入啮合时,每个离散齿的受力发生变化,导致传动不平稳。因此在结构设计时,可以通过齿廓修形乃至对波发生器轮廓进行修整,依据包络与反包络原理,使机构的重合度增大,提高传动的承载能力和平稳性。
6 结论1) 建立了离散齿谐波传动啮合副受力分析模型以及接触应力算法,并给出了啮合力和接触应力在接触面分布的计算与分析方法。
2) 对于刚轮齿形未发生顶切的离散齿传动结构,离散齿由进入到退出啮合的过程受力状态呈平稳变化趋势;刚轮靠近齿顶部位出现接触应力高,承载能力差的特点。
3) 对于刚轮齿形发生顶切的离散齿传动结构,在传动过程中,离散齿的受力状态会发生突变,影响传动的平稳性;相对于未发生顶切的情况,单个离散齿受力较大,影响传动的承载能力;在离散齿刚进入啮合的一段时间内,离散齿受力较大,接触应力高。
| [1] |
毛彬彬, 王克武.
谐波齿轮的齿形研究和发展概述[J]. 煤矿机械, 2008, 29(7): 6–8.
MAO Binbin, WANG Kewu. Research and development outlined of tooth profile of harmonic gear[J]. Coal Mine Machinery, 2008, 29(7): 6–8. (in Chinese) |
| [2] | 陈仕贤. 离散齿谐波传动: 中国, 200810172261. 6[P]. 2008-11-04. |
| [3] | Jiang S P, Zhang D X, Lin J B, et al. Application of harmonic drive gear in the ocean wave twin-floater generator[J]. Chinese Journal of Mechanical Engineering, 2004, 17(Sup): 107–109. |
| [4] | Kayabasi O, Erzincanli F. Shape optimization of tooth profile of a flexspline for a harmonic drive by finite element modelling[J]. Materials & Design, 2007, 28(2): 441–447. |
| [5] | Li Z, Melek W W, Clark C. Decentralized robust control of robot manipulators with harmonic drive transmission and application to modular and reconfigurable serial arms[J]. Robotica, 2009, 27(2): 291–302. DOI:10.1017/S0263574708004712 |
| [6] | Ostapski W. Analysis of the stress state in the harmonic drive generator-flexspline system in relation to selected structural parameters and manufacturing deviations[J]. Bulletin of the Polish Academy of Sciences:Technical Sciences, 2010, 58(4): 683–698. |
| [7] | Dhaouadi R, Ghorbel F H. Modelling and analysis of nonlinear stiffness, hysteresis and friction in harmonic drive gears[J]. International Journal of Modelling and Simulation, 2008, 28(3): 329–336. DOI:10.1080/02286203.2008.11442485 |
| [8] | Sensinger J W, Weir R F. Improved torque fidelity in harmonic drive sensors through the union of two existing strategies[J]. IEEE/ASME Transactions on Mechatronics, 2006, 11(4): 457–461. DOI:10.1109/TMECH.2006.878540 |
| [9] |
李剑锋, 董新蕊.
凸轮激波滚动活齿传动啮合力分析方法[J]. 机械工程学报, 2008, 44(5): 39–44.
LI Jianfeng, DONG Xinrui. Method of meshing force analysis for the movable rolling teeth transmission with cam actuating[J]. Chinese Journal of Mechanical Engineering, 2008, 44(5): 39–44. (in Chinese) |
| [10] | Dong H M, Wang D L, Ting K L. Elastic kinematic and geometric model of harmonic gear drives[C]//Proceedings of the ASME 2008 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, August 3-6, 2008, Brooklyn, New York, USA. New York:ASME, 2008, 2:717-725. |
| [11] | Kayabasi O, Erzincanli F. Shape optimization of tooth profile of a flexspline for a harmonic drive by finite element modeling[J]. Materials & Design, 2007, 28(2): 441–447. |
| [12] | Dhouib S, Hbaieb R, Chaari F, et al. Free vibration characteristics of compound planetary gear train sets[J]. Proceedings of the Institution of Mechanical Engineers. Part C, Journal of Mechanical Engineering Science, 2008, 228(8): 1389–1401. |
 2013, Vol. 36
2013, Vol. 36

