2. 重庆水利电力职业技术学院 电气工程系, 重庆 402160
2. Electrical Engineering Department, Chongqing Water Resources and Electric Engineering College, Chongqing 402160, China
根据目前生物医学与微电子学的发展以及国际上有关植入式电子系统最新研究的进展,体内植入器件的能量供给技术仍然是实现植入式系统的一项关键技术和难点。现阶段的植入电子器件主要采用电磁感应耦合的方法进行能量传递[1-3],该方法会对附近的医疗设备产生射频干扰,其体内线圈也是妨碍体内植入器件体积微型化的一大障碍。为克服电磁感应耦合供能方法的缺点,利用生物组织导电特性的经皮能量传递成为一种新型、有效且稳定的供能方案——容积导电[4]。
皮肤组织中存在大量的离子型体液,当皮肤处在电场中时,带电离子做定向运动形成电流场,因此可以通过这些带电离子将体外丰富的电能跨皮传递给体内植入电子器件的充电电池或者储能电容,维持植入器件长期、稳定、可靠地工作[5-6]。
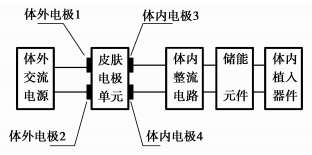
容积导电能量传递系统[7]如图 1所示,主要包括生物组织、电路、植入器件3部分。从目前发表的容积导电模型研究文献[8-9]来看,基本上是通过边界设置或等效参数的方法将容积导电的多场系统解耦为单一的“场”或“路”模型进行分析。“场”或“路”模型虽然在一定程度上降低了分析容积导电能量传递系统的复杂性,但是不能实时反映激励电源频率、幅值,电极形状布局对容积导电负载电压、电流波形,以及传递效率的影响。
|
图 1 容积导电能量传递框图 |
针对上述容积导电模型的不足,笔者考虑容积导电中电路与电场、电场与温度场的相互耦合关系,提出基于多场耦合的容积导电模型。该模型能够对容积导电系统进行整体性分析,易于在保证皮肤组织安全的前提下,探究各物理因素对能量传递效率的影响,优化容积导电能量传递系统性能。
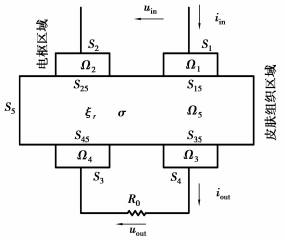
1 电场与电路耦合分析 1.1 电场与电路耦合物理模型容积导电“场”、“路”耦合物理模型如图 2所示,Ω1、Ω2、Ω3、Ω4为电极区域;Ω5为皮肤组织区域,含有传导电流和位移电流但不含源电流;S1、S2、S3、S4为电极与电路的连接边界;S15、S25、S35、S45为电极与皮肤组织的内部交界面;uin为施加在电极上的交变电压;iin为注入电极的外电流;R0为体内电路部分的等效电阻;uout为其输出电压;iout为该电路的电流。
|
图 2 容积导电电场与电路耦合物理模型 |
体外电压源对电极施加交变电压,在皮肤组织区域产生交变电场。该电场引起皮肤组织中的带电离子定向移动,从而在体内外电极间产生传导电流和位移电流,体内电极接受传递能量并向体内植入器件供电。因此,激励电源的频率,电极的形状布局,皮肤组织的导电率、介电常数都将影响能量传递的效率。
为了实现容积导电能量传递过程的模拟,笔者在皮肤电极区域按“场”的观点进行电磁场计算,而在电路上将这些电极与电源、电容、电阻等集总参数相连。这样以电压源为激励,电流作为未知量进行处理符合容积导电能量传递的实际情况。由于作为“场源”的电流iin需满足电路的外加电压约束, 因此该方法可以通过改变电压源参数(电压、频率)仿真模拟电路参数对能量传递效率的影响, 也可通过改变电极的几何参数研究能量传递效率的变化, 从而为优化容积导电系统提供理论指导。
1.2 准静态电场有限元求解容积导电能量传递系统的交流电压源频率低于100 kHz时,电磁波的波长大于3 000 m,远大于人体的3维尺寸。因此,把皮肤内的时变电磁场简化为准静态电场。
假设生物组织是各向同性的均匀介质,在皮肤、电极区域内,用磁场强度H和电场强度E表示的场方程和边界条件[10]为
| $ \left\{ \begin{array}{l} \nabla \times H = J + \frac{{\partial D}}{{\partial t}},\\ \nabla \times E = 0,\\ \nabla \cdot D = \rho ,\;\;\;\;\;\Omega \end{array} \right. $ | (1) |
| $ \int_s { - n \cdot \left( {J + \frac{{\partial D}}{{\partial t}}} \right)} = {i_{{\rm{in}}}}\;\;\;\;{S_1}、{S_2}, $ | (2) |
| $ \int_s {n \cdot \left( {J + \frac{{\partial D}}{{\partial t}}} \right)} = {i_{{\rm{out}}}}\;\;\;\;{S_3}、{S_4}, $ | (3) |
| $ n \cdot J = 0\;\;\;{S_5}, $ | (4) |
| $ n \cdot \left( {{\mathit{\boldsymbol{J}}_1} - {\mathit{\boldsymbol{J}}_2}} \right) = 0\;\;\;\;{S_{15}}、{S_{25}}、{S_{35}}、{S_{45}}, $ | (5) |
引入标量电位φ来描述电场强度,即E=-▽φ,则上述场方程可写成:
| $ \left. { - \frac{{{\varepsilon _0}{\varepsilon _r}{\nabla ^2}\left( {\partial \varphi } \right.}}{{\partial t}}} \right) - \nabla \cdot \left( {\sigma \nabla \varphi } \right) = 0\;\;\;\;\Omega , $ | (6) |
| $ \int_s { - n \cdot \left( {\sigma \left( {\nabla \varphi } \right) + {\varepsilon _0}{\varepsilon _r}\nabla \frac{{\partial \varphi }}{{\partial t}}} \right){\rm{d}}s} = {i_{{\rm{in}}}}\;\;\;\;{S_1}、{S_2}, $ | (7) |
| $ \int_s { - n \cdot \left( {\sigma \left( {\nabla \varphi } \right) + {\varepsilon _0}{\varepsilon _r}\nabla \frac{{\partial \varphi }}{{\partial t}}} \right){\rm{d}}s} = {i_{{\rm{out}}}}\;\;\;\;{S_3}、{S_4}, $ | (8) |
| $ \frac{{\partial \varphi }}{{\partial n}} = 0\;\;\;\;\;{S_5}, $ | (9) |
| $ {\sigma _1}\frac{{\partial {\varphi _a}}}{{\partial n}} - {\sigma _2}\frac{{\partial {\varphi _b}}}{{\partial n}} = 0\;\;\;\;{S_{15}}、{S_{25}}、{S_{35}}、{S_{45}}。$ | (10) |
其中:Ω为整个求解区域; σ为电导率; ε0为真空介电常数; εr为相对介电常数。对上述电场方程(6)~(10)采用加权余量法进行伽辽金有限元离散, 并整理, 式(6)转换成式(11):
| $ \begin{array}{l} \int_\mathit{\Omega } {\nabla \cdot \left[ {\left( {\sigma \nabla \varphi } \right){N_j}} \right]{\rm{d}}v} - \int_\mathit{\Omega } {\left[ {\nabla {N_j} \cdot \left( {\sigma \nabla \varphi } \right)} \right]{\rm{d}}v} + \\ \int_\mathit{\Omega } {\nabla \cdot \left[ {{N_j}{\varepsilon _0}{\varepsilon _r}\nabla \left( {\frac{{\partial \varphi }}{{\partial t}}} \right)} \right]{\rm{d}}v} - \int_\mathit{\Omega } {\left[ {\nabla {N_j} \cdot } \right.} \\ \left. {{\varepsilon _0}{\varepsilon _r}\nabla \left( {\frac{{\partial \varphi }}{{\partial t}}} \right)} \right]{\rm{d}}v = 0,\left( {j = 1,2, \cdots ,NP} \right); \end{array} $ | (11) |
其中:Nj为权函数; NP为节点总数。
根据边界条件式(7)~(10),对式(11)在整个求解域内进行空间离散化,可以得到一个时间的一阶微分方程组,将其矩阵形式表示为
| $ \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{M}}_\varphi } + \mathit{\boldsymbol{B}}\frac{{\partial {\mathit{\boldsymbol{M}}_\varphi }}}{{\partial t}} + \mathit{\boldsymbol{F}}i = 0, $ | (12) |
式中: A为劲度矩阵;B为阻尼矩阵;F为耦合劲度矩阵;Mφ为j节点位φ构成的N×1矩阵。
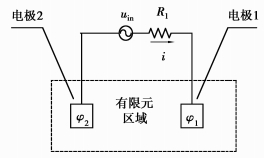
1.3 电场与电路耦合电路方程考虑离子型导电的特点和电极极化效应,容积导电能量传递系统采用交流激励源,体外场路耦合电路模型如图 3所示。
|
图 3 激励电源电路模型 |
体外电路回路方程为
| $ {u_{{\rm{in}}}} = i \cdot {R_1} + {\varphi _1} - {\varphi _2}, $ | (13) |
式中:uin为体外激励电压;i为回路电流;R1为电源等效内阻;φ1、φ2分别为电极1、2的电位。
写成矩阵即:
| $ \mathit{\boldsymbol{D}}{\mathit{\boldsymbol{M}}_\varphi } + {R_1}i = {u_{{\rm{in}}}}, $ | (14) |
其中:D为1×N矩阵,与φ1、φ2对应元素分别为1和-1,其余元素为0。
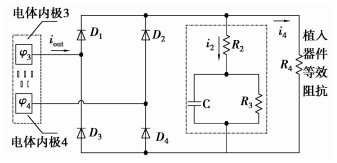
体外交流激励电压,通过皮肤传导到体内电极亦是交流电压,必须经AC/DC变换器将其变换为直流,才能向体内植入电池或者超级储能电容充电。由于超级电容具有充放电速度快、效率高、对环境无污染、循环寿命长、使用温度范围宽、安全性高等特点,笔者采用超级电容作为体内植入期间的储能电源。体内场、路耦合模型如图 4所示。
|
图 4 体内电路模型 |
右边虚线框内为储能超级电容[11]的等效电路, R2为等效串联内阻,R3为等效并联内阻, R4为植入器件等效电阻,C为等效电容, 二极管体D1、D2、D3、D4组成体内桥型整流电路[12],结构简单,有利于植入器件的微型化。
体内回路电路方程为
| $ \left( {{i_{out}} - {i_4}} \right) \cdot {R_2} + {U_c}\left( t \right) = {\varphi _3} - {\varphi _4}\left( {0 \le \omega t \le {\rm{ \mathit{ π} }}} \right), $ | (15) |
| $ {i_2} = C\frac{{{\rm{d}}{u_c}\left( t \right)}}{{{\rm{d}}t}} + \frac{{{u_c}\left( t \right)}}{{{R_3}}}, $ | (16) |
| $ {i_4} \cdot {R_4} = {\varphi _3} - {\varphi _4}\left( {0 \le \omega t \le {\rm{ \mathit{ π} }}} \right), $ | (17) |
联立公式(15)~(17)得:
| $ \left( {C\frac{{{\rm{d}}{u_c}}}{{{\rm{d}}t}} + \frac{{{u_c}}}{{{R_3}}}} \right){R_2} + {u_c} = {\varphi _3} - {\varphi _4}。$ | (18) |
其中:i2、i4为电容电流和植入器件电流;φ3、φ4分别为体内电极3、4的电位;uc(t)为储能超级电容电压。
写成矩阵即:
| $ \mathit{\boldsymbol{E}}{\mathit{\boldsymbol{M}}_\varphi } - \left( {1 + \frac{{{R_2}}}{{{R_3}}}} \right){u_c} - {R_2}C\frac{{{\rm{d}}{u_c}}}{{{\rm{d}}t}} = 0。$ | (19) |
其中:E为1×N矩阵,与φ3、φ4对应的元素分别为为1和-1,其余元素为0。
1.4 电场与电路耦合数学模型将式(12)与式(14)、(19)联立, 可得容积导电的场路耦合模型为
| $ \begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{A}}&\mathit{\boldsymbol{F}}&0\\ \mathit{\boldsymbol{D}}&{{R_1}}&0\\ \mathit{\boldsymbol{E}}&0&{ - \left( {1 + {R_2}/{R_3}} \right)} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{M}}_\varphi }}\\ i\\ {{u_c}} \end{array}} \right] + }\\ {\left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{B}}&0&0\\ 0&0&0\\ 0&0&{ - {R_2}C} \end{array}} \right]\frac{{\rm{d}}}{{{\rm{d}}t}}\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{M}}_\varphi }}\\ i\\ {{u_c}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 0\\ {{u_{{\rm{in}}}}}\\ 0 \end{array}} \right]。} \end{array} $ | (20) |
将其写成标准形式:
| $ \mathit{\boldsymbol{G}}X + H\frac{{{\rm{d}}X}}{{{\rm{d}}t}} = f, $ | (21) |
其中:
式(20)为时域模型,求解时需进行时间离散。笔者采用中心差分方法进行,其离散格式为
| $ \frac{{\mathit{\boldsymbol{H}}\left( {{X_{n + 1}} - {X_n}} \right)}}{{\Delta t}} + \frac{{\mathit{\boldsymbol{G}}\left( {{X_{n + 1}} + {X_n}} \right)}}{2} = \frac{{{\mathit{\boldsymbol{f}}_{n + 1}} + {\mathit{\boldsymbol{f}}_n}}}{2}, $ | (22) |
将式(21)代入,整理得:
| $ \begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} {\frac{B}{{\Delta t}} + \frac{A}{2}}&{\frac{F}{2}}&0\\ {\frac{D}{2}}&{\frac{{{R_1}}}{2}}&0\\ {\frac{E}{2}}&0&{ - \frac{{{R_2}C}}{{\Delta t}} - \frac{{\left( {{R_2} + {R_3}} \right)}}{{2{R_3}}}} \end{array}} \right]{{\left[ {\begin{array}{*{20}{c}} {{M_\varphi }}\\ i\\ {{u_c}} \end{array}} \right]}_{n + 1}} = }\\ {\left[ {\begin{array}{*{20}{c}} {\frac{B}{{\Delta t}} - \frac{A}{2}}&{ - \frac{F}{2}}&0\\ { - \frac{D}{2}}&{ - \frac{{{R_1}}}{2}}&0\\ { - \frac{E}{2}}&0&{ - \frac{{{R_2}C}}{{\Delta t}} + \frac{{\left( {{R_2} + {R_3}} \right)}}{{2{R_3}}}} \end{array}} \right]{{\left[ {\begin{array}{*{20}{c}} {{M_\varphi }}\\ i\\ {{u_c}} \end{array}} \right]}_n} + }\\ {\left[ {\begin{array}{*{20}{c}} 0\\ {\frac{{{u_{in.n + 1}} + {u_{in.n}}}}{2}}\\ 0 \end{array}} \right]。} \end{array} $ | (23) |
式(23)即为容积导电能量传递3维瞬态电磁场的场路耦合计算公式。所推导的场路耦合方法虽然增加了电流变量,但是方程系数的稀疏对称性的优点却得到了很好保持;只要知道激励电压条件uin,便可将此时的标量电位φ及瞬变电流i同时求解出来。因此,场路耦合方法,在电路层面上实现了容积导电能量传递的仿真,对能量传递效率的优化具有直接的指导意义。
2 电场与温度场耦合分析皮肤的传热属于生物传热学的研究范围, 与工程材料的传热很不一样,笔者采用Pennes的灌流组织传热模型[13]对皮肤的传热过程进行分析和仿真, 其形式为
| $ lC\frac{{\partial T}}{{\partial t}} = \nabla \left( {k\nabla T} \right) + {w_b}{C_b}{l_b}\left( {{T_b} - T} \right) + {Q_m}, $ | (24) |
式中: T、l、C、k分别为生物组织的温度、密度、比热和热导率;lb、Cb、Tb分别为动脉血的密度、比热和温度;w b为血液灌注率;Qm为代谢产热。
对于容积导电中单层皮肤不考虑新陈代谢产热, 血管和毛细血管传导热量,需考虑皮肤与环境间温度传递,传导电流引起的焦耳产热,将公式(24)变为
| $ lC\frac{{\partial T}}{{\partial t}} = \nabla \left( {k\nabla T} \right) + \lambda \left( {T - {T_E}} \right) + {Q_J}, $ | (25) |
| $ {Q_J} = E \cdot J = \sigma {\left( {\nabla \varphi } \right)^2}, $ | (26) |
将式(26)代入式(25)得电场、温度场的耦合微分方程:
| $ lC\frac{{\partial T}}{{\partial t}} = \nabla \left( {k\nabla T} \right) + \lambda \left( {T - {T_E}} \right) + \sigma {\left( {\nabla \varphi } \right)^2}, $ | (27) |
其中:λ为一个综合的换热系数[14],它包含了辐射、对流、出汗等因素;TE为环境温度;QJ为皮肤组织求解域内的焦耳热密度。通过QJ的引入,成功实现了容积导电皮肤组织中温度场与电场的耦合。
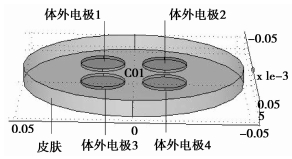
3 容积导电能量传递有限元模型人体皮肤由3部分构成:上皮(Epidermis)、真皮层(Dermis)和皮下组织层(Subcutaneousissue), 其厚度随人体的不同部位而变化, 以胸部皮肤为例, 使用软件FEM 3.5建立容积导电能量传递模型, 如图 5所示。该模型由以下部分组成:激励电源、体外电极、人体皮肤组织、体内电极、体内整流电路和储能超级电容、植入器件构成。
|
图 5 体内外电极布置示意图 |
使用软件FEM 3.5建立容积导电能量传递模型的具体参数如下:体外电极1、2取为圆柱体, 之间距离d=0.024 m, 其半径×高为0.01 m×0.001 m, 人体皮肤的半径×高为0.05 m×0.006 m; 其中体内电极3、4正对体外电极1、2, 用于接收体外电极传递的能量;体内采用如图 4所示电路,R2=1 mΩ, R3=10 000 Ω,R4=50 Ω, C=0.5F。虽然利用软件FEM3.5将容积导电的电路与电场进了物理耦合,但图 5并没有显示电路部分。
为减小电极与皮肤的接触阻抗, 电极选择具有良好导电性能的电极材料(Ag/AgCl),其电导率为5 000 s/m。皮肤的介电特性可以从文献[15-16]数据库中获得,如表 1所示。
| 表 1 皮肤介电特性 |
在单层结构模型中, 皮肤组织的热特性参数取为: ρ=ρb=1 000 kg/m3,C=Cb=4 180 J/(kg·K), k=0.162 7 W/(m·K), λ=8.36 W/(m2·K), 文献和实验普遍证实正常状态下, 体表温度为32~34 ℃, 这里取为33℃。
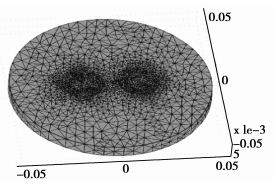
将皮肤电极单元剖分(如图 6所示)为41 700个小四面体组成的离散单元,对电场与电路耦合方程进行离散,得到离散方程组见式(23),并利用软件FEM3.5提供的线性求解器对其进行求解,计算电路中的电流、电压波形、皮肤组织中的电场分布。离散并求解公式(27)得到皮肤组织中温度时空分布。
|
图 6 四面体有限元栅格 |
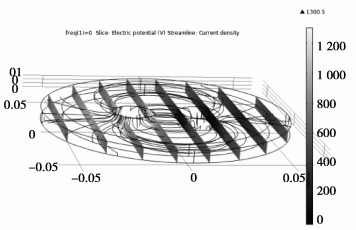
在激励电源采用uin=10 sin(2π×5 000 t)V, 环境温度T= 26.6 ℃条件下, 使用电磁场有限元分析软件FEM3.5计算皮肤电极单元中电位和电流线分布,如图 7所示。
|
图 7 电势和电流密度场线 |
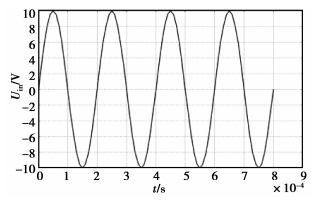
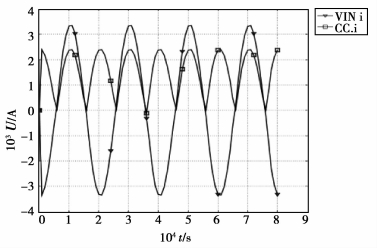
图 8为激励电源电压波形,图 9为充电初期电源与储能电容的电流波形,比较两图可以看出,电源输出电流超前其电压45°左右,与皮肤组织为容性阻抗相一致。从图 9可以得到容积导电电流传递效率
|
图 8 激励电源波形 |
|
图 9 电源与储能电容电流波形 |
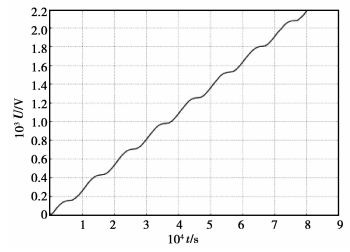
桥型整流电路输出的直流电流正向流经储能电容,其电压随时间近似直线上升,如图 10所示。这种电压随时间大幅度上升表明超级电容可以在短时间内吸收能量。只要合理设计皮肤电极单元的电极布局,匹配电路的输入、输出阻抗,就能使储能电容电压最终稳定在需要值,如2.5 V。此时,电容储能为
| $ {w_e} = \frac{1}{2}C{U^2} \approx 0.4{\rm{mAh}}, $ |
|
图 10 储能电容电压 |
考虑到一般情况下,标称容量为40 mAh的锂离子纽扣电池可供植入心脏起搏器正常工作15年,由此推知,该容量满足以2个月为充电时间周期的心脏起搏器对供能电源的要求。
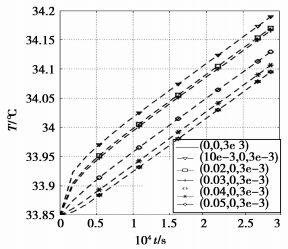
皮肤组织温度的时空分布如图 11所示,温度随充电时间逐渐上升,充电时间持续8 h,皮肤组织的温度上升约为1 ℃,达34 ℃,该温度不会对人体组织造成伤害。其中,最高温度出现在皮肤几何中心处,坐标为(0,0,0.003)。
|
图 11 皮肤组织温度时空分布 |
笔者通过研究三维电场、温度场的有限元求解,在此基础上引入容积导电电路回路方程,推导了容积导电能量传递多场耦合有限元模型。该模型考虑了电场与温度场,电路与电场之间的耦合关系,在电路层面上实现了容积导电能量传递数值仿真。利用有限元软件FEM3.5仿真计算了电源、储能电容的电流和电压波形,以及皮肤组织的温度变化,从多物理视角验证了容积导电供能方案的可行性,为进一步研究安全、可靠、高效的容积导电能量传递模型奠定基础。
| [1] | Ho S L, Wang J H, Fu W N, et al. A comparative study between novel witricity and traditional inductive magnetic coupling in wireless charging[J]. IEEE Transactions on Magnetics, 2011, 47(5): 1522–1525. DOI:10.1109/TMAG.2010.2091495 |
| [2] | Ng D C, Bai S, Yang J, et al. Wireless technologies for closed-loop retinal prostheses[J]. Journal of Neural Engineering, 2009, 6(6): 065004. DOI:10.1088/1741-2560/6/6/065004 |
| [3] | Chen H Y, Jia W Y, Yang Q X, et al. Coupling and compensation analysis of transcutaneous energy transmission for implantable artificial heart[C]//Proceedings of the 2009 IEEE 35th Annual Northeast Bioengineering Conference, April 3-5, 2009, Boston, MA. Piscataway: IEEE Press, 2009: 1-2. |
| [4] | Sun M G, Justin G A, Roche P A, et al. Passing data and supplying power to neural implants[J]. IEEE Engineering in Medicine and Biology Magazine, 2006, 25(5): 39–46. DOI:10.1109/MEMB.2006.1705746 |
| [5] | Tang Z D, Sun C, Sclabassi R J, et al. Circuit model of battery recharging by volume conduction[C]//Proceedings of the IEEE 32nd Annual Northeast Bioengineering Conference, April 1-2, 2006, Easton, PA, USA. Piscataway: IEEE Press, 2006: 123-124. |
| [6] | Zhao Y, Tang Z D, Huang L H, et al. Research of the modal of volume conduction energy transfer[C]//Proceedings of the 2008 World Automation Congress, September 28-October 2, 2008, Hawaii, HI. Piscataway: IEEE Press, 2008: 1-4. |
| [7] | Tang Z D, Sclabassi R J, Sun C X, et al. Transcutaneous battery recharging by volume conduction and its circuit modeling[C]//Proceedings of the 28th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, August 30-September 3, 2006, New York, NY. Piscataway: IEEE Press, 2006: 644-647. |
| [8] |
唐治德, 吴明鹏, 余小闯, 等.
植入医学器件的电能供给及电磁场仿真[J]. 重庆大学学报, 2010, 33(9): 56–61.
TANG Zhide, WU Mingpeng, YU Xiaochuang, et al. Power supply and electromagnetic simulation of implantable medical devices[J]. Journal of Chongqing University, 2010, 33(9): 56–61. DOI:10.11835/j.issn.1000-582X.2010.09.010 (in Chinese) |
| [9] | Hackworth S A, Sun M G, Sclabassi R J. Skin-electrode circuit model for use in optimizing energy transfer in volume conduction systems[C]//Proceedings of the 31st Annual International Conference of the IEEE Engineering in Medicine and Biology Society, September 3-6, 2009, Minneapolis, Minnesota, USA. Piscataway: IEEE Press, 2009: 4508-4551. |
| [10] | Grant P F, Lowery M M. Electric field distribution in a finite-volume head model of deep brain stimulation[J]. Medical Engineering & Physics, 2009, 31(9): 1095–1103. |
| [11] |
蔡国营, 王亚军, 谢晶, 等.
超级电容器储能特性研究[J]. 电源世界, 2009, 38(1): 33–38.
CAI Guoying, WANG Yajun, XIE Jing, et al. Research on the energy-storage characteristics of super capacity[J]. The World of Power Supply, 2009, 38(1): 33–38. (in Chinese) |
| [12] | Ma J M, Yang Q X, Chen H Y. Transcutaneous energy and information transmission system with optimized transformer parameters for the artificial heart[J]. IEEE Transactions on Applied Superconductivity, 2010, 20(3): 798–801. DOI:10.1109/TASC.2010.2043241 |
| [13] |
迪丽娜·马合木提, 江世臣, 张学学, 等.
皮肤组织传热过程的研究[J]. 西安交通大学学报, 2006, 40(3): 369–372.
MAHEMUTY Dilina, JIANG Shichen, ZHANG Xuexue, et al. Investigation to heat conduction model in skin tissue[J]. Journal of Xi'an Jiaotong University, 2006, 40(3): 369–372. (in Chinese) |
| [14] |
卓子寒, 冯礼, 王旭飞, 等.
直接接触加热治疗皮肤疾病的温度场仿真分析[J]. 航天医学与医学工程, 2010, 23(1): 42–46.
ZHUO Zihan, FENG Li, WANG Xufei, et al. Emulating analysis of the temperature field for hyperthermia treatment of skin diseases with direct heating[J]. Space Medicine & Medical Engineering, 2010, 23(1): 42–46. (in Chinese) |
| [15] | Federal Communications Commission. Body tissue dielectric parameters[EB/OL]. [2011-01-21] http://transition.fcc.gov/oet/rfsafety/dielectric.html. |
| [16] | Institute for Applied Physics. Dielectric properties of body tissues[EB/OL]. [2011-01-28] http://niremf.ifac.cnr.it/tissprop/. |
 2013, Vol. 36
2013, Vol. 36

