2. 重庆市电力科学试验研究院, 重庆 401123;
3. 安徽合肥供电公司, 合肥 230000
2. Chongqing Electric Power Test & Research Institute, Chognqing 401123, China;
3. Hefei Power Supply Office, Hefei 230000, China
输电线路地面标称电场是分析特高压直流线路对环境影响的重要指标之一,有些国家把最大标称电场限值作为线路设计必须满足的环境指标。同时,地面标称电场既是确定线路走廊宽度和两旁拆房范围的依据之一,也是确定多种线路交叉跨越距离的决定性因素[1]。标称电场强度的准确计算对输电线路下方地面合成电场值也起着至关重要的作用。
径向基函数(RBF)法采用配点形式,求解中无需背景网格支持,彻底摆脱网格的限制,是纯粹的无网格法。与基于网格的方法不同,无网格方法只需要节点的信息,不需要节点与节点之间的信息,这样就克服了网格法,比如有限元法计算中网格畸变和重新生成带来的困难,而且计算时间和计算机内存也比有限元法要节省很多。
在电磁场计算中, 应用无单元Galerkin法的研究工作较多[2-8], 将径向基函数法应用于电磁场的数值计算最近几年引起一定关注[9-12], 而将径向基函数法应用于输电线周围电场的计算还较鲜见。
数值计算中,常用的RBF有:Multiquadric(MQ)函数:φ=(c2+r2)γ;逆MQ函数:φ=(c2+r2)-γ;高斯分布函数:φ=exp(-a2r2);薄板样条函数:φ=rklnr;三次样条函数:φ=r3。
考虑到MQ函数在插值中的广泛应用,同时它在微分方程求解中具有指数收敛特性和高精度的优点,因此,笔者将MQ函数的径向基函数法应用到特高压直流输电导线下方地面标称电场计算中,通过合理的布点和形状参数的设置,求解双极直流输电导线下方地面的标称电场,通过与已有文献方法对比,验证该方法的有效性和准确性,并讨论线路参数对地面标称场的影响,为求解输电线周围空间电场提供了一种新思路。
1 径向基函数的基本原理 1.1 径向基函数的定义通俗讲,径向基函数即为距离基函数,它以空间距离r为变量,故具有简便直观和各向同性优点。Stein[9]和Weiss[13]将径向函数定义为:满足‖x1‖=‖x2‖时就有φ(x1)=φ(x2)的函数φ,即它仅依赖于r=‖x‖的函数,式中范数为Euclidean范数;径向函数也可定义为[10, 14]:径向量的连续实值函数Φ(x)=φ(r)=φ(‖x-c‖),x∈Rd,范数与前面一样,c为径向基函数中心。一定条件下,﹛φ(x-xi)﹜线性无关便可形成径向基函数空间中的一组基,当{xj}几乎充满R时,﹛φ(x-xi)﹜及其线性组合即可逼近空间内几乎所有函数。
1.2 径向基函数法求解输电线路标称电场的原理与实施步骤径向基函数法求解输电线电场方法的基本原理为:用径向基函数(RBF)的线性组合近似表示待求位函数,对RBF中心位置、形状参数和配点进行设置,进而将位函数的边值方程转化为以RBF表示的离散配点方程,再利用域内和边界配点条件组装配点方程求权系数λi,即可求得域内任意点的电位φ,从而求出任意点的电场。具体实施步骤如下:
1) 建立模型。在建模时假设地面为无穷大导体平面,导线为无限长直且与地面平行的圆柱体导体,其表面等电位。以双极直流n分裂导线为例建立直流输电线的边值方程和求解模型,如图 1所示。
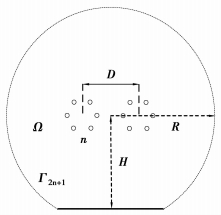
|
图 1 计算模型 |
以分裂导线的中心为圆心,以R为半径作圆与地面相交组成一个封闭的边界Г2n+1,由于R足够大,因此可以认为在此边界上电位φ(x,y)=0,而每根子导线表面的电位边界φ(x,y)=U。子导线和边界Г2n+1所包围的空间即为可求解区域(Ω)。
于是此问题的求解转化为求满足以下边值方程的解:
| $ \left\{ \begin{array}{l} {\nabla ^2}\varphi = \frac{{{\partial ^2}\varphi \left( {x,y} \right)}}{{\partial {x^2}}} + \frac{{{\partial ^2}\varphi \left( {x,y} \right)}}{{\partial {y^2}}} = {f_0}\left( {x,y} \right),\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {x,y} \right) \in \Omega ;\\ \varphi \left( {x,y} \right) = {f_1}\left( {x,y} \right),\;\;\;\;\;\;\;\left( {x,y} \right) \in {{\bf{\Gamma }}_1},{{\bf{\Gamma }}_2} \cdots {{\bf{\Gamma }}_{2n}};\\ \varphi \left( {x,y} \right) = {f_2}\left( {x,y} \right),\;\;\;\;\;\;\;\left( {x,y} \right) \in {{\bf{\Gamma }}_{2n + 1}}; \end{array} \right. $ | (1) |
式中:f0(x, y)=0, f1(x, y)=U, f2(x, y)=0;Г1,Г2…Г2n, 为每根子导线表面边界;Г2n+1为圆与地面组成的封闭边界。
2) 选择径向基函数。选择二维形式的MQ函数为RBF插值函数,其形式为
| $ {\varphi _i}\left( {x,y} \right) = \sqrt {{{\left( {x - {c_{ix}}} \right)}^2} + {{\left( {y - {c_{iy}}} \right)}^2} + \alpha _i^2} , $ | (2) |
式中:i为插值函数的个数。
于是任意点的待求位函数可由径向基函数序列表示为
| $ \begin{array}{l} \varphi \left( {x,y} \right) = \sum {{\lambda _i}{\varphi _i}\left( {x,y} \right)} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\sum {{\lambda _i}\sqrt {{{\left( {x - {c_{ix}}} \right)}^2} + {{\left( {y - {c_{iy}}} \right)}^2} + \alpha _i^2} } , \end{array} $ | (3) |
式中:λi为权系数。
3) 配点设置。在求解区域(Ω)内配置M个节点,在子导线表面边界Г1, Г2,…,Г2n上配置N个节点,在边界Г2n+1上配置P个节点,RBF函数数目和配点数为Q=M+N+P。
4) 形成离散配点方程组,求得权系数λi。由于近似函数在配点处满足插值条件,把式(2)、(3)代入方程组(1)中, 形成离散配点方程组为
| $ \left\{ \begin{array}{l} \sum\limits_{i = 1}^M {{\lambda _i}{{\phi ''}_i}\left( {{x_j},{y_j}} \right)} = {f_0}\left( {x,y} \right),\left( {j = 1,2,L,M} \right);\\ \sum\limits_{i = 1}^M {{\lambda _i}{\phi _i}\left( {{x_j},{y_j}} \right)} = {f_1}\left( {x,y} \right),\left( {j = M + 1,L,M + N} \right)L;\\ \sum\limits_{i = 1}^M {{\lambda _i}{\phi _i}\left( {{x_j},{y_j}} \right)} = {f_2}\left( {x,y} \right),\left( {j = M + N + 1,L,Q} \right); \end{array} \right. $ | (4) |
式中:
| $ {{\phi ''}_i}\left( {{x_j},{y_j}} \right) = \frac{{{{\left( {x - {c_{ix}}} \right)}^2} + {{\left( {y - {c_{iy}}} \right)}^2} + 2\alpha _i^2}}{{{{\left[ {{{\left( {x - {c_{ix}}} \right)}^2} + {{\left( {y - {c_{iy}}} \right)}^2} + \alpha _i^2} \right]}^{1.5}}}}。$ | (5) |
式(4)写成矩阵形式为
| $ \mathit{\Phi }\lambda = f。$ | (6) |
针对上式,并应用最小二乘法得权系数为
| $ \lambda = {\left( {{\mathit{\Phi }^{\rm{T}}}\mathit{\Phi }} \right)^{ - 1}}{\mathit{\Phi }^{\rm{T}}}f。$ |
5) 求域内任意点电位。在求得RBF插值函数的权系数λ后,域内任一点P的电位φp(x, y),即可通过式(3)求得,即
| $ {\varphi _{\rm{p}}}\left( {x,y} \right) = \sum {{\lambda _i}{\phi _i}\left( {{x_{\rm{p}}},{y_{\rm{p}}}} \right)} = {\mathit{\Phi }_{\rm{p}}}\lambda 。$ |
6) 计算场量。根据获得的任意点电位函数φ(x, y),可得任意一点的电场强度为
| $ {E_{\rm{p}}}\left( {x,y} \right) = - \nabla \varphi \left( {{x_{\rm{p}}},{y_{\rm{p}}}} \right), $ | (7) |
代入P点坐标即可求得此点的电场值。
7) 准确性验证。把计算所得电场值与解析解或已有文献值比较,计算其误差,验证算法的准确性。
2 实例仿真与验证分析 2.1 同轴电缆模型同轴电缆模型示意图如图 2所示,其中R1=1.0 cm, R2=3.0 cm, ε=2ε0,内导体壳和外导体壳之间存在电压U=300 V,分析介质中电场分布。

|
图 2 电缆模型 |
根据高斯定理,可求得该模型的解析解为
| $ E = U/\left[ {R\ln \left( {{R_2}/{R_1}} \right)} \right],\left( {{R_1} < R < {R_2}} \right)。$ |
该模型可看做单根输电线路的求解模型,因为二者具有相类似的边值条件。用RBF法求解的布点和参数设置,如图 3所示。

|
图 3 配点和测点分布 |
1) 域内布点:以中心为圆心, 于R1和R2之间, 以半径r=(1+n×0.25)cm(n=1, 2,…,7)作圆,每个圆上均匀分布20个离散点;
2) 边界布点:在内壳表面和外壳内侧表面均匀设置20个离散点,取上述离散点作为RBF中心点和配点;
3) 测点布置:沿x轴正方向,在R1和R2之间, 以d1=0.01 cm等间距布置测试点。
计算时取内壳表面电压为400 V,外壳表面电压为100 V,形状参数α取10。此模型的边值方程为
| $ \left\{ \begin{array}{l} \frac{{{\partial ^2}\varphi \left( {x,y} \right)}}{{\partial {x^2}}} + \frac{{{\partial ^2}\varphi \left( {x,y} \right)}}{{\partial {y^2}}} = 0,\;\;\;\;\left( {x,y} \right) \in \mathit{\Omega };\\ \varphi \left( {{x_i},{y_i}} \right) = 400,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {{x_i},{y_i}} \right) \in {\mathit{\Gamma }_1};\\ \varphi \left( {{x_j},{y_j}} \right) = 100,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {{x_j},{y_j}} \right) \in {\mathit{\Gamma }_2}。\end{array} \right. $ |
式中:Ω为求解的域内区域;Г1为内芯表面边界;Г2为外芯内侧表面边界。
通过仿真计算,求得RBF法和解析解的电场强度曲线对比,如图 4所示。
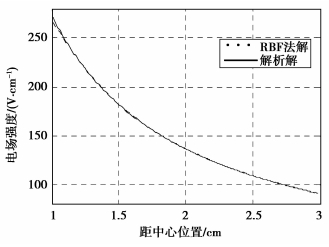
|
图 4 RBF法和解析解的电场强度值 |
RBF法和解析解的相对误差分布曲线如图 5所示。
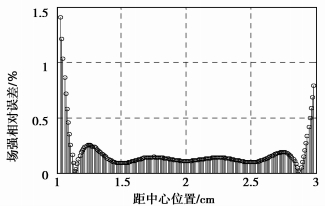
|
图 5 电场强度的相对误差曲线 |
数据分析:从图 4、5可以看出,RBF法计算的电场和解析解吻合很好。经计算,RBF法和解析解的最大相对误差仅为1.4%,且绝大部本点的相对误差小于0.2%;相对均方根误差值RMSE为1.73×10-5。RMSE是反映整体相对误差的一个度量值,其定义为:
| $ RMSE = \sqrt {\frac{{\sum\limits_i {\Delta f_i^2} }}{{\sum\limits_i {f_i^2} }}} = \sqrt {\frac{{\sum\limits_i {{{\left( {{E_{i\_{\rm{exact}}}} - {E_{i\_{\rm{calc}}}}} \right)}^2}} }}{{\sum\limits_i {{{\left( {{E_{i\_{\rm{exact}}}}} \right)}^2}} }}} $ |
式中:Ei_exact为第i个测点的准确值;Ei_calc为计算值。
2.2 双极六分裂输电线模型为了能与已有文献的结果进行对比,笔者采用文献[15]中的计算参数:导线型号为6×LGJ-720/50;子导线半径为18.1 mm;导线分裂间距为450 mm;极导线间距为22.0 m;极导线高度h分别为18.5、21.0、23.0 m;电压为±800 kV,模型示意如图 1所示。
布点和形状参数设置如图 6所示。
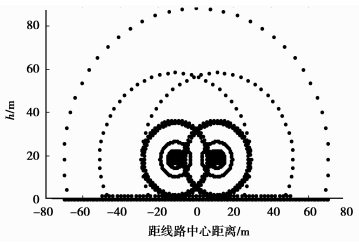
|
图 6 配点和测点分布 |
1) 域内布点:在域内分别以两极导线中心为圆心、以半径为0.25×2n m(n=0, 1, 2, …, 5)和16.5,17,17.5,18 m作圆,每个圆上均匀分布60个离散点;以半径为40 m作圆,取地面以上的离散点。
2) 边界布点:此时共有12根导线,式(1)中n=6。在每根导线表面均匀设置10个点,并以双极导线的中心为圆心、以半径为70 m作圆与地面相交组成一个封闭的边界,在此边界上均匀分布190个离散点,取上述离散点作为RBF中心点和配点。
3) 测点布点:以离地面高度1.5 m, 水平方向从-50 m到50 m以0.25 m等间距布置400个测试点,计算时形状参数α取0.88。
用RBF法求解的电场强度值与文献[15]中采用的镜像法求解值对比,如图 7所示。
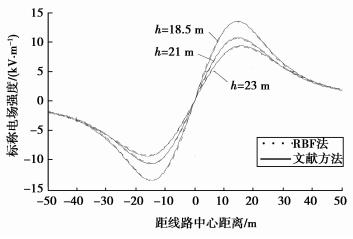
|
图 7 RFB方法与文献方法得到的标称场强比较 |
在极导线不同高度时,对RBF法与文献方法求得的标称场强相对误差进行分析。绘制极导线高度h为18.5 m时相对误差的分布曲线,如图 8所示。由于标称场强分布关于原点对称,只截取了从0到50 m作误差曲线图。
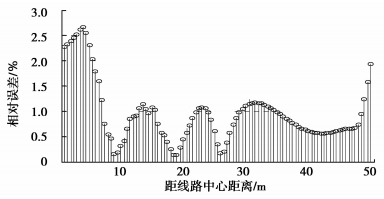
|
图 8 标称场强的相对误差曲线 |
数据分析:从图 7、8可看出RBF法求解电场强度和文献中的值吻合很好。经计算,极导线高度h分别为18.5、21.0、23.0 m时,RBF法与文献中数据的相对误差最大值分别为:2.7%,3.1%,2.2%;相对均方根误差值RMSE分别为:2.1×10-4,4.3×10-3,1.7×10-4。通过本例,可以看出此法精度较高。
3 线路参数对地面标称场强的影响从上面模型可以看出导线高度对地面标称场强的影响。从图 7可见:随着导线高度的增加,地面标称场强的幅值明显减小;距离导线越远,导线高度对标称场强的影响越小。下面用RBF法继续讨论不同参数对地面标称场强的影响。
3.1 次导线半径的影响图 9为次导线半径分别为1,2,3 cm时,用RBF法求得地面标称场强的计算结果。从图中可以看出,随着子导线半径的增大,地面标称场强的幅值略有增加。这与文献[16]中所述标称场强的趋势相吻合。
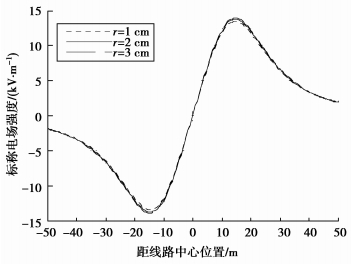
|
图 9 次导线半径不同时的地面标称电场强度 |
图 10为分裂根数分别为4根、6根和8根时,用RBF法求得的地面标称场强的计算结果。从图中知,随着导线分裂数增加,地面标称场强的幅值略有增加。这与增加导线半径的影响规律相同,这是因为增加分裂导线的作用等效于扩大导线半径。
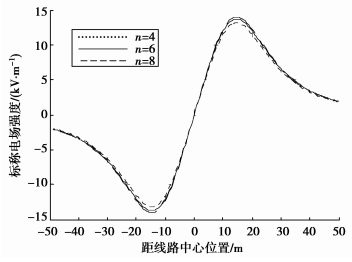
|
图 10 导线分裂数不同时地面标称电场强度 |
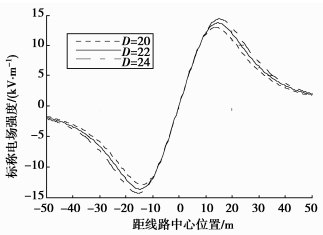
图 11为导线极间距分别为20,22,24 m时,用RBF法求得的地面标称场强的计算结果。由图可见,地面标称场强幅值随极间距增加而增加,这是因为异极性导线对地表标称场强的抵消作用随极间距的增大而减小;地面标称场强取得幅值时距线路中心距离随着极间距的增大而增大,幅值出现在导线外侧2~3 m处。
|
图 11 极间距不同时地面标称电场强度 |
1) 给出基于径向基函数的无网格法求解直流输电线地面标称电场的方法、原理和实施步骤。
2) 用RBF法解得的电缆内部的电场和模型的解析解吻合很好;用此法求得的直流输电线下地面标称电场强度具有较高的计算精度。
3) 用RBF法讨论了不同导线参数对直流输电线地面标称电场的影响。结果表明:导线对地高度和极间距离,对地面标称电场强度的影响较大;导线越高地面标称电场强度越小,极间距离越大地面标称电场强度越大;次导线半径和分裂根数对地面标称电场强度的影响较小。
| [1] | 薛荣. ±800kV特高压直流输电线路导线电场计算方法的研究[D]. 重庆: 重庆大学, 2007. |
| [2] | Parreira G F, Silva E J, Fonseca A R, et al. The element-free Galerkin method in three-dimensional electromagnetic problems[J]. IEEE Transactions on Magnetics, 2006, 42(4): 711–714. DOI:10.1109/TMAG.2006.872014 |
| [3] | Bottauscio O, Chiampi M, Manzin A. Element-free Galerkin method in eddy-current problems with ferromagnetic media[J]. IEEE Transactions on Magnetics, 2006, 42(5): 1577–1584. DOI:10.1109/TMAG.2005.863932 |
| [4] |
刘素贞, 杨庆新.
二维电场的无单元数值解法[J]. 河北工业大学学报, 1999, 28(2): 10–15.
LIU Suzhen, YANG Qingxin. Element-free method applied to 2D electrical field numerical calculation[J]. Journal of Hebei University of Technology, 1999, 28(2): 10–15. (in Chinese) |
| [5] |
茅昕光, 林鹤云.
电磁场数值分析的无单元Galerkin方法[J]. 东南大学学报:自然科学版, 2003, 33(1): 30–33.
MAO Xinguang, LIN Heyun. Element free Galerkin method for numerical analysis of electromagnetic fields[J]. Journal of Southeast University:Natural Science Edition, 2003, 33(1): 30–33. (in Chinese) |
| [6] |
倪培宏, 杨仕友.
无网格伽辽金法及其在电磁场数值计算中的应用[J]. 电机与控制学报, 2003, 7(1): 26–29.
NI Peihong, YANG Shiyou. The element free Galerkin method and its application in numerical computations of electromagnetic fields[J]. Electrical Machines and Control, 2003, 7(1): 26–29. (in Chinese) |
| [7] |
赵美玲, 聂玉峰, 左传伟.
电磁场计算中的无网格局部Petrov-Galerkin方法[J]. 电机与控制学报, 2005, 9(4): 397–400, 405.
ZHAO Meiling, NIE Yufeng, ZUO Chuanwei. Local petrov-galerkin method for electromagnetic field computation[J]. Electric Machines and Control, 2005, 9(4): 397–400, 405. (in Chinese) |
| [8] |
杨庆新, 刘素贞, 陈海燕.
三维无单元伽辽金法及其在电磁场数值分析中的应用[J]. 电工技术学报, 2006, 21(9): 116–121.
YANG Qingxin, LIU Suzhen, CHEN Haiyan. Three-dimensional element free Galerkin method and its applications in electromagnetic field numerical analysis[J]. Transactions of China Electrotechnical Society, 2006, 21(9): 116–121. (in Chinese) |
| [9] | 张淮清. 电磁场计算中的径向基函数无网格法研究[D]. 重庆: 重庆大学, 2008. http://cdmd.cnki.com.cn/Article/CDMD-10611-2009047770.htm |
| [10] |
张淮清, 俞集辉.
电磁场边值问题求解的径向基函数方法[J]. 高电压技术, 2008, 36(2): 531–536.
ZHANG Huaiqing, YU Jihui. Radial basis function method for boundary value problems in electromagnetic field[J]. High Voltage Engineering, 2008, 36(2): 531–536. (in Chinese) |
| [11] |
张淮清, 俞集辉, 郑亚利.
径向基函数及其耦合方法在电磁场数值计算中的应用[J]. 计算物理, 2009, 26(2): 299–310.
ZHANG Huaiqing, YU Jihui, ZHENG Yali. Radial basis functions and coupled method in computational electromagnetics[J]. Chinese Journal of Computational Physics, 2009, 26(2): 299–310. (in Chinese) |
| [12] | Yu J H, Zhang H Q. Solving waveguide eigenvalue problem by using radial basis function method[C]//Proceedings of the World Automation Congress, September 28-October 2, 2008, Hawaii, HI. Piscataway: IEEE Press, 2008: 1-5. |
| [13] | Stein E M, Weiss G L. Introduction to fourier analysis on euclidean spaces[M]. New Jersey: Princeton University Press, 1971. |
| [14] |
吴宗敏.
径向基函数、散乱数据拟合与无网格偏微分方程数值解[J]. 工程数学学报, 2002, 19(2): 1–12.
WU Zongmin. Radial basis function scattered data interpolation and the meshless method of numerical solution of PDEs[J]. Chinese Journal of Engneering Mathmatics, 2002, 19(2): 1–12. (in Chinese) |
| [15] |
王毅, 孙成秋, 汤涛, 等.
不同运行方式下特高压直流输电线路的地面电场与离子流分布[J]. 电网技术, 2008, 32(2): 29–33.
WANG Yi, SUN Chengqiu, TANG Tao, et al. Distribution of ground electric field strength and ionic current density under different operating modes of UHVDC transmission lines[J]. Power System Technology, 2008, 32(2): 29–33. (in Chinese) |
| [16] |
田冀焕, 邹军, 刘杰, 等.
高压直流双回输电线路合成电场与离子流的计算[J]. 电网技术, 2008, 32(2): 61–65, 70.
TIAN Jihuan, ZOU Jun, LIU Jie, et al. Calculation of total electric field and ionic current density of double-circuit HVDC transmission lines[J]. Power System Technology, 2008, 32(2): 61–65, 70. (in Chinese) |
 2013, Vol. 36
2013, Vol. 36

