单边核磁共振仪[1-9]相对于传统的封闭式核磁共振仪来说,其结构开放不包含被测物,可从物体表面对被测物进行检测,同时体积较小便于携带,因而广泛应用于食品分析和质量控制、材料科学领域、地球物理领域等。在单边核磁共振仪中主磁场的产生主要依赖于永磁体,典型磁体结构有U型磁体[10],Halbach磁体[11],以及桶状[10]等。同时永磁体也有被用来产生梯度磁场,文献[10]中指出单根条状磁体在其上下表面中心沿着磁化方向上一段距离内,磁场具有较好的梯度特性。在假设高磁导率材料表面为等标量磁位面的基础上,利用分离变量法设计出一种在水平方向产生均匀场,而垂直方向产生梯度磁场的磁体结构[12]。
综上所述,目前所设计的单边核磁共振磁体因不可产生梯度磁场需要额外梯度线圈,但单边核磁共振的梯度线圈设计理论尚不成熟,而利用分离变量法设计的磁体可产生梯度磁场,但结构封闭难以应用于单边核磁共振中。因此目前没有提出一种无需梯度线圈的单边磁体结构设计方法。
笔者拟通过数据拟合的方法对传统Halbach磁体的结构进行改进和优化,得到一种新的单边磁体结构,它在指定区域内产生的磁场,水平方向上具有较好的平坦特性,垂直方向上梯度变化特性,同时具有一定的均匀区域, 磁体结构不需额外的梯度线圈[13],简化了梯度编码系统设计。
1 磁体磁场计算关于永磁体磁场的计算采用以磁荷法为基础的标量磁位法[14],为了提高计算精度,使用二阶有限元算法[15],得到如下有限元方程:
| $ K\varphi = R, $ | (1) |
| $ {K_{ij}} = \int_{{V_e}} {\mu \nabla {N_i}{\rm{dV, }}\mathit{i}{\rm{, }}\mathit{j} \in {\rm{1, 2, }} \cdots {\rm{, 10, }}} $ | (2) |
| $ {\mathit{R}_i} = \int_{{S_e}} {\mathit{\boldsymbol{n}} \cdot {\mathit{\boldsymbol{B}}_r}{N_i}{\rm{d}}\mathit{s}\;\;\mathit{i} \in {\rm{1, 2, }} \cdots {\rm{, 6, }}} $ | (3) |
其中:n为磁体表面的单位外法向量;Br为磁体的剩磁;Ni为二阶四面体单元的形状函数。标量磁位φ被求出后便可得到永磁体周围空间磁场分布。
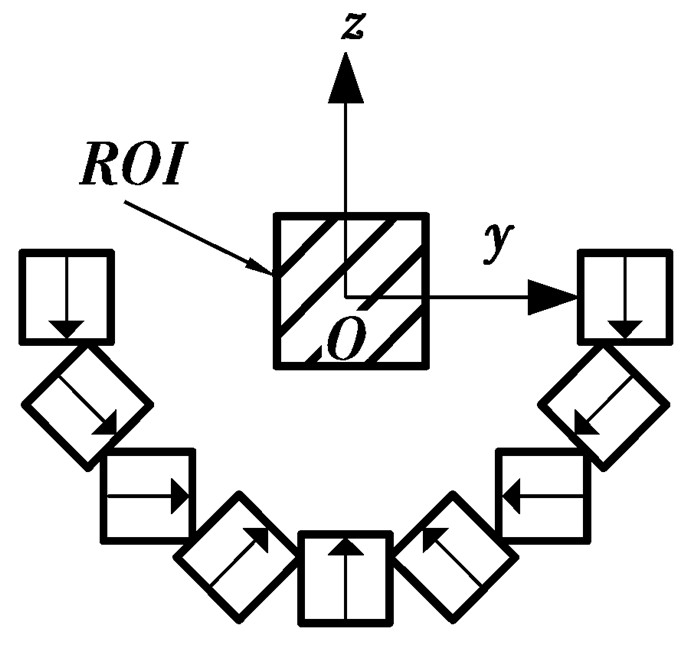
2 单边磁体结构Halbach磁体可在其圆柱空腔内产生均匀磁场,因而受到人们关注。图 1为16个形状大小及剩磁完全相同的磁棒搭建的Halbach磁体[11]。但其结构封闭难以应用于单边核磁共振中,因此仅保留下方9个磁棒,如图 2所示。

|
图 1 Halbach磁体结构 |
|
图 2 单边磁体结构 |
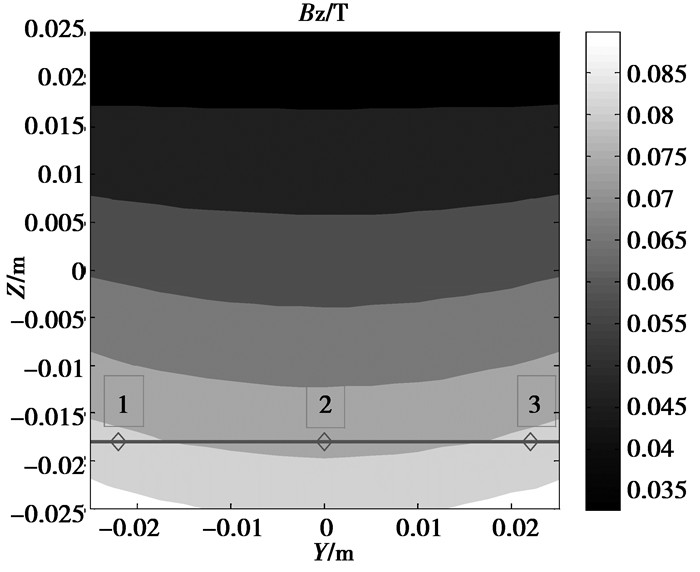
图中磁体尺寸为3 cm×3 cm×10 cm,剩磁为1.28T,箭头表示剩磁方向。在YOZ平面内以坐标原点为中心,5 cm长的正方形区域ROI内绘制磁场的Z轴分量,如图 3所示。
|
图 3 ROI区域磁场Bz分量等位线 |
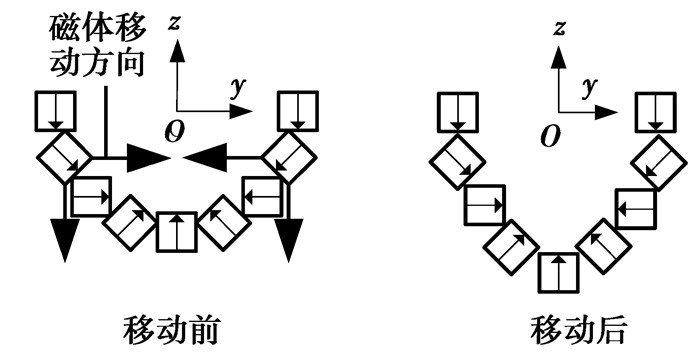
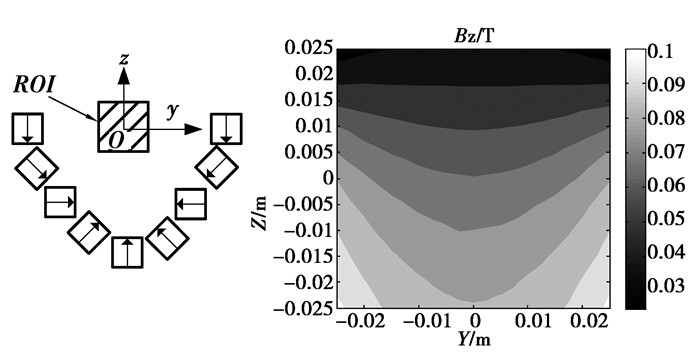
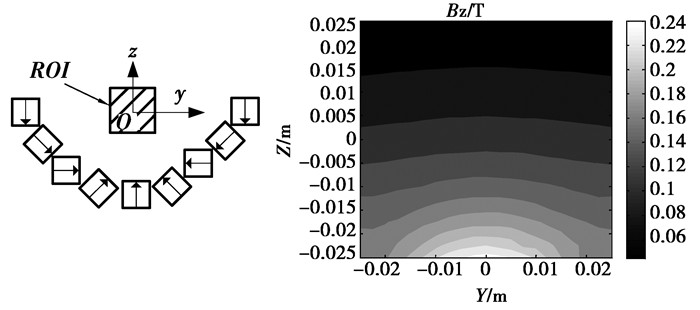
从图 3可以看出,磁场沿Z轴方向呈现近似梯度变化,且等位线向Z轴负方向凹陷。其原因是1,3两点到磁体的距离较近,磁场较强,而2点到磁体的距离较远,磁场较弱。因此可以推断:若将图 2中两边磁体向Y轴中间移动,同时将磁体向下移(图 7中结构1),见移动示意图 4,则ROI区域内磁场等位线将向下凹陷更厉害,如图 5所示;若对图 2磁体进行相反操作(图 7中结构3),则ROI内磁场等位线将向Z轴上方凹陷,如图 6所示。
|
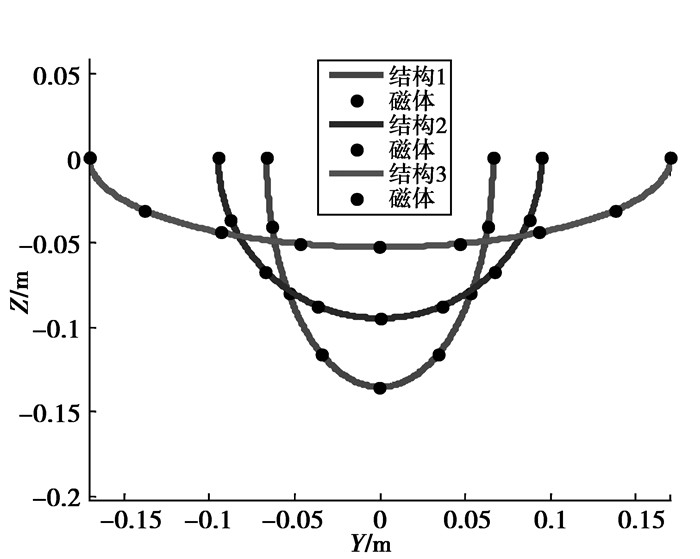
图 7 3种磁体结构 |
|
图 4 磁体结构移动示意图 |
|
图 5 磁体结构1及其在ROI内磁场等位线 |
|
图 6 磁体结构3及其在ROI内磁场等位线 |
图 7中的结构1对应于图 2结构。从图 7可以看出,当磁体结构由1到2再到3时,磁体中心所在曲线逐渐平坦,而ROI区域内等位线则由向在Z轴负方向凹陷(图 5)到稍微平坦(图 3)再到向Z轴正方向凹陷(图 6),因此必然存在一种磁体结构,它在ROI区域内产生的磁场等位线平坦特性最好,且具有近似梯度分布特性,而这种磁体结构和磁场正是单边核磁共振所需要的。
3 磁体结构优化对于图 7所示的不同磁体结构,可以用椭圆曲线来模拟,让磁体中心点等弧长摆放在椭圆曲线上,通过调节椭圆半长轴长度来改变磁体结构。
YOZ平面内的椭圆方程如下所示:
| $ \frac{{{y^2}}}{{{a^2}}} + \frac{{{z^2}}}{{{b^2}}} = 1, $ | (2) |
式中:a,b为椭圆半长轴和半短轴的长度。为了便于磁体结构优化,添加如下约束条件,而仅保留一个独立变量a:
| $ \mathit{a} \cdot \mathit{b = r} \cdot \mathit{r = }{\mathit{r}^2}, $ | (3) |
r为Halbach磁体[17]中心所在圆周半径,此时磁体结构仅由a决定,当a < b以及a=b=r和a>b时,可分别实现图 7所示3种磁体结构。
为了描述等位线的平坦特性,在ROI区域内沿Z轴方向上等间距选取21条线段,每条线段上等间距选取21点,形成441个格点,分别计算每条线段上各点的磁场Z轴分量。用下面公式近似表征该区域等位线图的平坦特性:
| $ {\rm{Std = }}\frac{1}{\mathit{n}}\sum\limits_{i = 1}^n {st{d_i},} $ | (4) |
| $ {\rm{St}}{{\rm{d}}_i}{\rm{ = }}\frac{1}{m}\sqrt {{{\sum\limits_{j = 1}^m {\left( {{B_{zij}} - \overline {{B_{zi}}} } \right)} }^2}} , $ | (5) |
其中Bzij为第i条线段上第j个点的磁场Z轴分量;
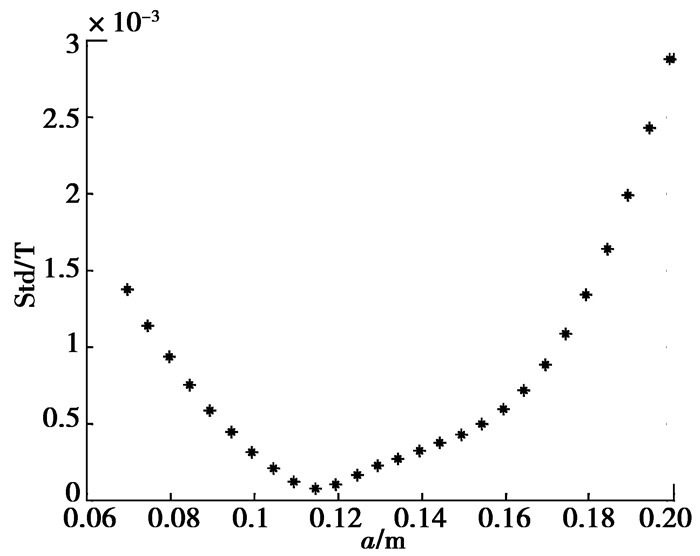
让公式(2)中椭圆半长轴a从0.7r开始,以0.05r为步进,逐渐变化到2r,分别计算每种磁体结构在ROI区域内磁场Z轴分量等位线的Std值,以a为横坐标,Std为纵坐标,绘出散点图如图 8所示。
|
图 8 Std关于半长轴a的散点图 |
观察图 8可以发现Std关于a的散点图存在最低点,为了寻找最低点的位置,对数据点进行拟合。由于使用一般多项式拟合时,拟合方程呈现病态特性,使得计算误差较大,因此利用正交多项式做数据拟合[16]。正交多项式采用Gram-Schmidt正交化方法产生:
| $ {\mathit{P}_\mathit{k}} = {x^k}-\sum\limits_{j = 0}^{k-1} {{a_{jk}}{P_j}\left( x \right), k = 0, 1, \cdots, m, } $ | (6) |
| $ \begin{gathered} {a_{jk}} = \frac{{\sum\limits_{i = 0}^n {{x^k}{P_j}\left( {{x_i}} \right)} }}{{\sum\limits_{i = 0}^n {P_j^2\left( {{x_i}} \right)} }}, \mathit{j = }{\rm{0, 1, }} \cdots \mathit{, k}{\rm{-1}}\mathit{, } \hfill \\ \mathit{k = }{\rm{0, 1, }} \cdots \mathit{, m, } \hfill \\ \end{gathered} $ | (7) |
拟合系数为
| $ {a_j} = \frac{{\sum\limits_{i = 0}^n {{f_i}{P_j}\left( {{x_i}} \right)} }}{{\sum\limits_{i = 0}^n {P_j^2\left( {{x_i}} \right)} }}, \mathit{j = }{\rm{0, 1, }} \cdots \mathit{, m, } $ | (8) |
拟合方程为
| $ \mathit{y = }\sum\limits_{i = 0}^m {{a_j}{P_j}\left( x \right)} 。$ | (9) |
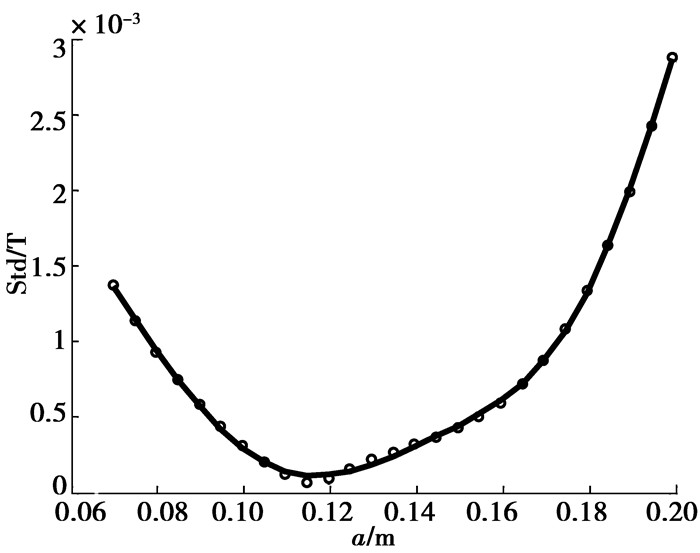
逐渐提高拟合多项式次数,便可找到平方误差满足要求的拟合方程。笔者拟合平方误差要求小于10-8,得到拟合方程(下式)和拟合曲线(见图 9)。
|
图 9 Std关于半长轴a的拟合曲线 |
| $ \begin{array}{l} {\rm{Std =-242}}\;{\rm{676}}{\rm{.4}}{\mathit{a}^7} + 213\;909{a^6}-78\;124.2{a^5} + \\ 15\;294.2{a^4}-1\;730.7{a^3} + 113.55{a^2} - 4.06a + 0.083\;8, \end{array} $ | (10) |
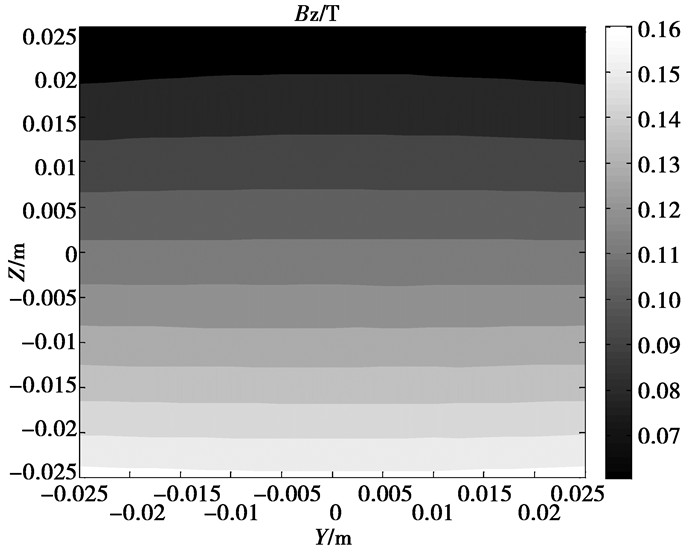
让拟合方程(10)对变量a求导,得到与最低点对应的a值为0.116 7 m,与其对应的磁场Bz分量等位线图如图 10所示。
|
图 10 最优磁体结构磁场Z轴分量等位线 |
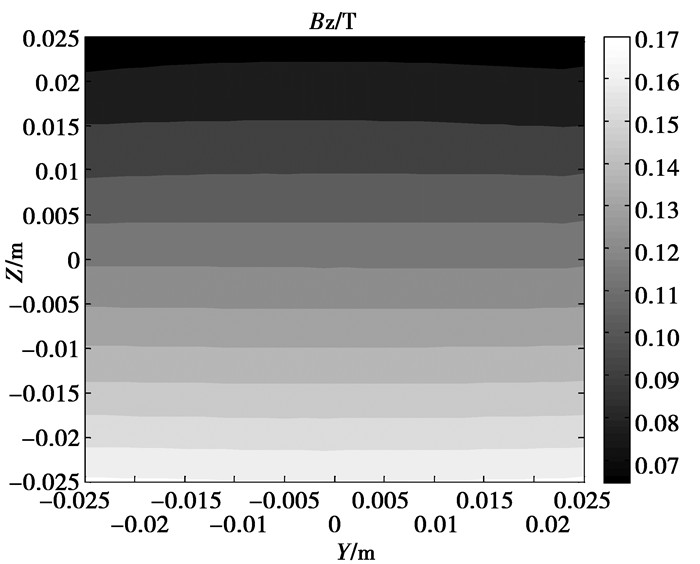
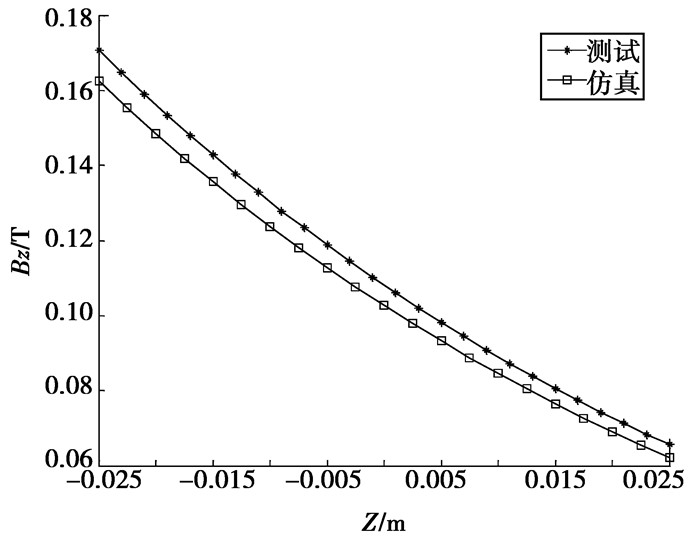
根据所设计磁体尺寸,购买所需的磁体模块,搭建磁体系统(见图 11),在三维磁场测量平台(见图 12)上测量磁体系统在ROI区域内产生的磁场,如图 13,14所示。

|
图 11 实际磁体系统 |

|
图 12 三维磁场测量平台 |
|
图 13 磁体系统磁场的Z轴分量实测等位线图 |
|
图 14 磁体系统在Z轴上磁场Z轴分量的实测值和仿真值变化规律比较 |
从图 10、图 13和图 14可以看出,磁场Z轴分量的仿真计算值和实测值均具有较好的平坦特性,且磁场沿Z轴方向具有较好的梯度特性,梯度约为:2 mT/mm。图 13和14中磁场Z轴分量的实测值虽然比仿真计算值稍大些, 但并不会影响整体磁场的平坦特性和梯度变化特性。测量值稍微偏大的原因可能为:
1) 仿真计算用的磁体单元剩磁为1.28T,而实际购买磁体单元之间存在差异,其剩磁不能精确为1.28T。
2) 测量磁场的贝尔高斯计存在一定测量误差。
3) 三维磁场测量平台存在测量点的定位误差。
同时对不同高度的Z平面磁场进行仿真计算,发现在z=17 mm高度上,-2 mm < x < 2 mm, -2 mm < y < 2 mm, 范围内磁场较为均匀,均匀度为1.3×10-3,场强为0.073 9T,由于该区域面积较小,考虑到测量和定位误差,并未对该区域进行实际测量。
4 总语笔者对半边Halbach磁体的结构进行改进和优化,得到一种新的单边Halbach结构磁体,根据优化结果搭建了实际磁体结构,该结构磁场的仿真计算和实际测量结果均表明,它可在50 mm×50 mm区域内产生平坦特性和梯度特性较好(2 mT/mm)的磁场, 且在4 mm×4 mm区域内获得均匀度为1.3×10-3,场强为0.073 9T的磁场,对于这样的均匀度,相对于单边核磁共振中6.0×10-4~1.0×10-3的均匀度要求来说,还具有一定的差距。笔者工作还存在一定的不足之处:优化过程仅仅针对磁体结构,而不包括磁体模块的磁化方向;由于仅以磁场的梯度特性为优化目标,并未对磁场均匀度进行优化。针对不足,可在现有磁体结构的基础上,以均匀度为优化目标,改变磁体模块的磁化方向,以获得均匀度和梯度性能较好的单边磁体结构。
| [1] | Chang W H, Chen J H, Hwang L P. Single-sided mobile NMR apparatus using the transverse flux of a single permanent magnet[J]. Magnetic Resonance Imaging, 2010, 28(1): 129–138. DOI:10.1016/j.mri.2009.05.039 |
| [2] | Demas V, Prado P J. Compact magnets for magnetic resonance[J]. Magnetic Resonance in Porous Media, 2008, 1081: 36–39. |
| [3] | Badea E, Miu L, Budrugeac P, et al. Study of deterioration of historical parchments by various thermal analysis techniques complemented by SEM, FTIR, UV-Vis-NIR and unilateral NMR investigations[J]. Journal of Thermal Analysis and Calorimetry, 2009, 91(1): 17–27. |
| [4] | Capitani D, Proietti N, Gobbino M, et al. An integrated study for mapping the moisture distribution in an ancient damaged wall painting[J]. Analytical Bioanalytical Chemistry, 2009, 395(7): 2245–2253. DOI:10.1007/s00216-009-3170-5 |
| [5] | Senni L, Caponero M, Casieri C, et al. Moisture content and strain relation in wood by Bragg grating sensor and unilateral NMR[J]. Wood Science and Technology, 2010, 44(1): 165–175. DOI:10.1007/s00226-009-0268-z |
| [6] | Federico E D, Centeno S A, Kehlet C, et al. Unilateral NMR applied to the conservation of works of art[J]. Analytical Bioanalytical Chemistry, 2010, 396(1): 213–220. DOI:10.1007/s00216-009-3128-7 |
| [7] | Pourmand P, Wang L, Dvinskikh S V. Assessment of moisture protective properties of wood coatings by a portable NMR sensor[J]. Journal of Coatings Technology and Research, 2011, 8(5): 649–654. DOI:10.1007/s11998-011-9348-8 |
| [8] | Masic A, Chierotti M R, Gobetto R, et al. Solid-state and unilateral NMR study of deterioration of a Dead Sea Scroll fragment[J]. Analytical Bioanalytical Chemistry, 2012, 402(4): 1551–1557. DOI:10.1007/s00216-011-5265-z |
| [9] | Proietti N, Presciutti F, Tullio V D, et al. Unilateral NMR, 13C CPMAS NMR spectroscopy and micro-analytical techniques for studying the materials and state of conservation of an ancient Egyptian wooden sarcophagus[J]. Analytical Bioanalytical Chemistry, 2011, 399(9): 3117–3131. DOI:10.1007/s00216-010-4229-z |
| [10] | Blümich B, Perlo J, Casanova F. Mobile single-sided NMR[J]. Progress in Nuclear Magnetic Resonance Spectroscopy, 2008, 52(4): 197–269. DOI:10.1016/j.pnmrs.2007.10.002 |
| [11] | Raich, H, Blümler P. Design and construction of a dipolar halbach array with a homogeneous field from identical bar magnets:NMR mandhalas[J]. Concepts in Magnetic Resonance, 2004, 23B(1): 16–25. DOI:10.1002/cmr.b.v23b:1 |
| [12] | Glover P M, Aptaker P S, Bowler J R, et al. A novel high-gradient permanent magnet for the profiling of planar films and coatings[J]. Journal of Magnetic Resonance, 1999, 139(1): 90–97. DOI:10.1006/jmre.1999.1772 |
| [13] | 熊国欣, 李立本. 核磁共振成像原理[M]. 北京: 科学出版社, 2007. |
| [14] |
刘福贵, 杨庆新.
三维永久磁铁磁场的标量磁位数值计算[J]. 河北工业大学学报, 1997, 26(3): 49–54.
LIU Fugui, YANG Qingxin. Magnetic scalar potential finite element method applied in 3-D permanent magnetic fields[J]. Journal of Hebei University of Technology, 1997, 26(3): 49–54. (in Chinese) |
| [15] | 金建铭. 电磁场有限元方法[M]. 西安: 西安电子科技大学出版社, 1998. |
| [16] | 王开荣, 杨大地. 应用数值分析[M]. 北京: 高等教育出版社, 2010. |
 2013, Vol. 36
2013, Vol. 36

