在机械传动中,齿轮副是最常见的一类传动形式,而非圆锥齿轮作为一种新型的齿轮传动形式,能够实现相交轴之间的变速比传动。目前,为了传递相交轴间的非匀速比运动,通常采用非圆齿轮与锥齿轮的组合机构或其他复合机构。这些机构大多具有机构复杂,体积庞大、传递效率低等缺点。椭圆锥齿轮副能够实现相交轴之间的变速比传动,且具有体积小、结构紧凑、运动平稳、传动效率高等优点,具有很大的发展潜力。但由于高阶椭圆锥齿轮节曲线设计复杂,加工和制造也相当困难,严重阻碍了高阶椭圆锥齿轮的发展。随着高阶椭圆锥齿轮研究的深入,其设计理论日趋成熟,继高阶椭圆锥齿轮的数学模型提出之后[1-2],又实现了其三维计算机辅助设计[3]。目前五轴数控加工方法被用于该锥齿轮的加工制造[4],虽然可以加工得到齿轮实体,但是要评价其精度却十分困难。对比直齿锥齿轮测量不难知道,由于直齿锥齿轮几何形状以及测试原理的复杂性,相关齿轮齿距偏差和齿距累积误差测量及评价的方法[5-7],其测量技术远远落后于直齿圆柱齿轮。高阶椭圆锥齿轮副由于其节曲线不是平面曲线,而是一条空间球面曲线,现有的测齿工具均不适用。
研究高阶椭圆锥齿轮副可知,在其设计过程中,均以建立球面节曲线方程开始,并在此基础上设计齿廓等特征,因此高阶椭圆锥齿轮的球面节曲线在其研究中起基础作用。以高阶椭圆锥齿轮插齿包络法加工得到的齿轮实体为基础,利用三坐标测量技术,提出了高阶椭圆锥齿轮测量的数学模型和评定方法,并验证了高阶椭圆锥齿轮插齿包络法以及齿轮实体的正确性。
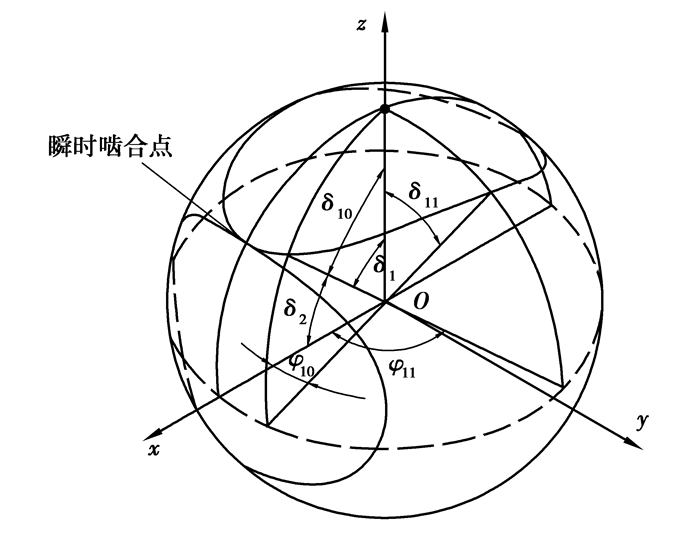
1 椭圆锥齿轮节曲线和球面弧长齿轮副的传动可以看作一对节曲面纯滚动。椭圆锥齿轮可以等同于椭圆节锥面的纯滚动。根据椭圆锥齿轮设计原理知道,在设计过程中,一旦给定齿轮副的传动比关系,便可得到椭圆锥齿轮副的球面节曲线方程,从而得到相应的节锥面。如图 1所示,令该椭圆锥齿轮副瞬时锥角满足δ1+δ2=π/2,则瞬时传动比为
| $ {i_{21}} = {{\rm{d}}_{\varphi 2}}/{{\rm{d}}_{\varphi 1}} = \tan {\delta _1} = \cot {\delta _2}, $ | (1) |
|
图 1 椭圆锥齿轮副节曲线示意图 |
式中δ1,δ2分别为主、从动齿轮的瞬时锥角。
设椭圆锥齿轮副的传动比函数[8]为
| $ {i_{21}} = \frac{{1 + {e^2} - 2e\;\cos \;n{\varphi _1}}}{{1 - {e^2}}}, $ | (2) |
式中:e为偏心率;n为椭圆锥齿轮阶数;
分别以主动轮和从动轮轴线为z轴建立球面坐标系,根据几何关系,主、从动轮球面节曲线方程[3, 9]可表示为
| $ \left\{ \begin{array}{l} {r_1} = R\sin {\delta _1}\cos {\varphi _1}{i_1} + R\sin \;{\delta _1}\sin {\varphi _1}{j_1} + R\cos {\delta _1}{k_1}, \\ {r_2} = R\sin {\delta _2}\cos {\varphi _2}{i_2} + R\sin \;{\delta _2}\sin {\varphi _2}{j_2} + R\cos {\delta _2}{k_2}。\end{array} \right. $ | (3) |
联立式(1)~式(3),得到δ1、δ2、
| $ \left\{ \begin{array}{l} {\delta _1}{\rm{ = }}\arctan \frac{{1 + {e^2} - 2e\cos n{\varphi _1}}}{{1 - {e^2}}}, \\ {\delta _2} = {\rm{arccot}}\frac{{1 + {e^2} - 2e\cos n{\varphi _1}}}{{1 - {e^2}}}, \\ {\varphi _2} = \frac{{1 + {e^2}}}{{1 - {e^2}}}{\varphi _1} - \frac{{2e}}{{n\left( {1 - {e^2}} \right)}}\sin n{\varphi _1}。\end{array} \right. $ | (4) |
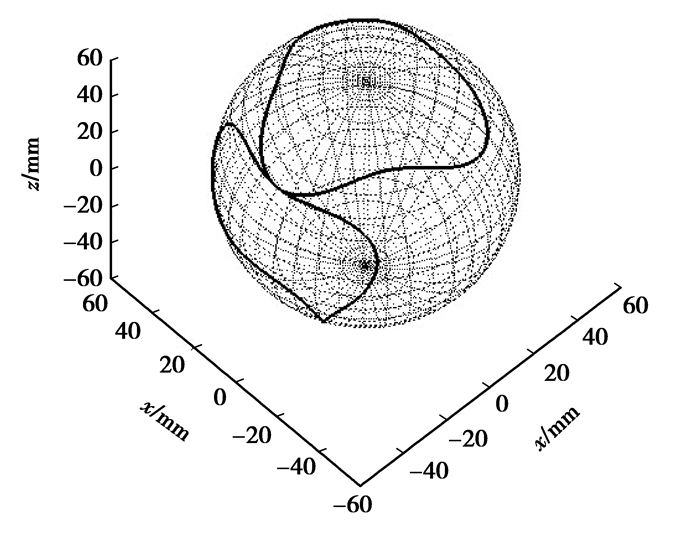
联立式(3)、式(4),得到椭圆锥齿轮的节曲线方程。通过Matlab程序绘制出各阶椭圆锥齿轮的非圆节曲线。以三阶为例,取参数n=3,e=0.15,球面半径R=51.16 mm,如图 2所示。
|
图 2 三阶椭圆锥齿轮副的节曲线 |
椭圆锥齿轮的节曲线是空间的变性椭圆,理论设计加工中是利用范成包络方法加工得到的齿轮,其齿廓在节曲线各个位置各不相同,但是大端节曲线上的齿距是相等的。联立式(1)~式(4),利用球面弧长积分公式得到球面节曲线的长度[10]
| $ L = R\int \begin{array}{l} {\varphi _{11}}\\ {\varphi _{10}} \end{array} \;\sqrt {{{\sin }^2}\delta + {\delta ^2}\left( \varphi \right)} {\rm{d}}\varphi, $ | (5) |
式中:R为齿轮的球面半径;
联立式(1)~式(5)可知,球面弧长积分公式的被积函数表达式相当复杂,根本无法直接求解,故采用数值积分法进行求解。这里采用的Romberg积分法是根据Richardson外推技巧,利用变步长的复化梯形公式推导出的数值积分法,其公式[11]为
| $ \left\{ \begin{array}{l} {T_0}\left( h \right) = T\left( h \right), \\ {T_m}\left( h \right) = \frac{{{T_{m - 1}}\left( {\frac{h}{2}} \right) - {{\left( {\frac{1}{2}} \right)}^{2m}}{T_{m - 1}}\left( h \right)}}{{1 - {{\left( {\frac{1}{2}} \right)}^{2m}}}} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{{4^m}{T_{m - 1}}\left( {\frac{h}{2}} \right) - {T_{m - 1}}\left( h \right)}}{{{4^m} - 1}}, \end{array} \right. $ | (6) |
式中,T(h)是将[a,b]区间n=2i等分后构造的复化梯形公式,由式(6)产生的Tm(h)逼近积分
以二阶椭圆锥齿轮为例,其齿数z=38,偏心率e=0.15,球面半径R=52.33 mm,令积分误差限ε=10-6,利用Matlab软件,采用的Romberg积分法可以得到理论齿距fp2=5.143 032 mm。同理,可以得到三阶、四阶椭圆锥齿轮的理论齿距,此理论齿距为标准齿距值。表 1所示为各阶椭圆锥齿轮的标准齿距值,表中各参数均与齿轮实体样件设计参数一致[4]。
| 表 1 高阶椭圆锥齿轮标准齿距值 |
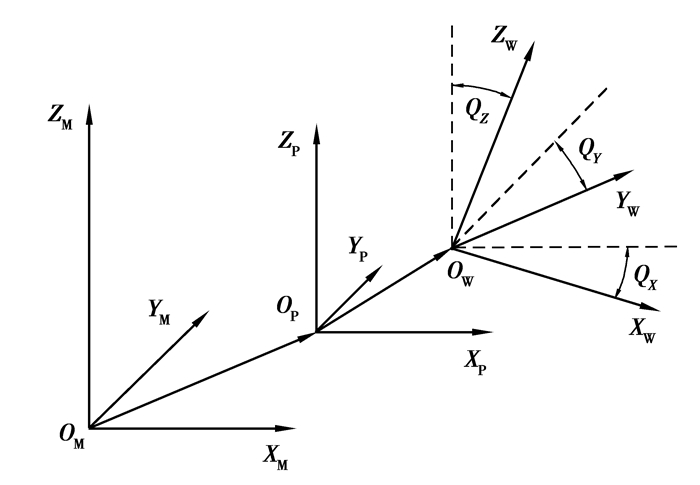
在三坐标测量机中,若测量时未建立工件坐标系,则计算机默认工件坐标系OW与测量机床坐标系OM重合。如图 3所示,在测量当中涉及到3个坐标系的转换关系[12]。
|
图 3 坐标系关系示意图 |
1) 三坐标测量机坐标系OM:所有测量都是在该坐标系内进行,用XM,YM,ZM分别表示三坐标轴。
2) 测量工作台坐标系OP:工件放置在测量工作台面上测量,其三坐标轴分别于测量坐标系的坐标轴平行,分别用XP,YP和ZP表示。
3) 工件坐标系OW:和齿轮固联在一起。三坐标轴分别用XW,YW和ZW表示。
测量工作平台坐标系与测量坐标系的关系为
| $ \left[\begin{array}{l} {X_{\rm{P}}}\\ {Y_{\rm{P}}}\\ {Z_{\rm{P}}} \end{array} \right] = \left[\begin{array}{l} {X_{\rm{M}}}\\ {Y_{\rm{M}}}\\ {Z_{\rm{M}}} \end{array} \right] - {\mathit{\boldsymbol{O}}_\mathit{\boldsymbol{\rm{M}}}}{\mathit{\boldsymbol{O}}_\mathit{\boldsymbol{\rm{P}}}}。$ | (7) |
测量工作平台坐标系与工件坐标系的关系为
| $ \left[\begin{array}{l} {X_{\rm{M}}}\\ {Y_{\rm{M}}}\\ {Z_{\rm{M}}}\\ 1 \end{array} \right] = \left[\begin{array}{l} {X_{\rm{P}}}\\ {Y_{\rm{P}}}\\ {Z_{\rm{P}}}\\ 1 \end{array} \right] \cdot \mathit{\boldsymbol{T}} \cdot \mathit{\boldsymbol{R}}, $ | (8) |
其中T为平移矩阵,R为旋转矩阵。平移矩阵可以表示为
| $ \mathit{\boldsymbol{T}} = \left[{\begin{array}{*{20}{c}} 1&0&0&0\\ 0&1&0&0\\ 0&0&4&0\\ {{X_{{O_{\rm{P}}}}}-{X_{{O_{\rm{W}}}}}}&{{Y_{{O_{\rm{P}}}}}-{Y_{{O_{\rm{W}}}}}}&{{Z_{{O_{\rm{P}}}}}-{Z_{{O_{\rm{W}}}}}}&1 \end{array}} \right]。$ | (9) |
变换矩阵R则根据找正后工件轴的方向系数计算。设与工件轴平行的单位向量为
| $ \begin{array}{l} \mathit{\boldsymbol{n = }}\mathit{a}\mathit{\boldsymbol{i + }}\mathit{b}\mathit{\boldsymbol{j + }}\mathit{c}\mathit{\boldsymbol{k = }}\\ \;\;\;\;{\rm{cos}}\;{\mathit{Q}_x}\mathit{\boldsymbol{i + }}{\rm{cos}}\;{\mathit{Q}_y}\mathit{\boldsymbol{j + }}{\rm{cos}}\;{Q_z}\mathit{\boldsymbol{k}}, \end{array} $ | (10) |
则有
| $ \mathit{\boldsymbol{R = }}\left[{\begin{array}{*{20}{c}} {\sqrt {{b^2} + {c^2}} }&{\frac{{-ab}}{{\sqrt {{b^2} + {c^2}} }}}&{\frac{{-ac}}{{\sqrt {{b^2} + {c^2}} }}}&0\\ 0&{\frac{c}{{\sqrt {{b^2} + {c^2}} }}}&{\frac{{-b}}{{\sqrt {{b^2} + {c^2}} }}}&0\\ a&b&c&0\\ 0&0&0&1 \end{array}} \right]。$ | (11) |
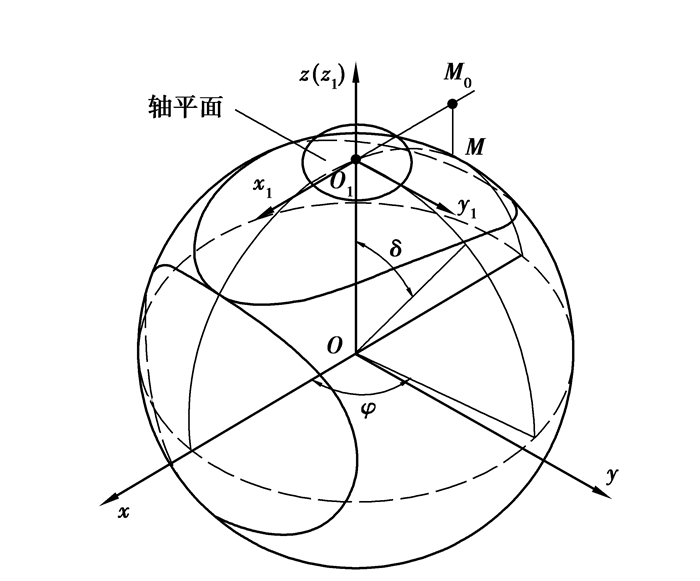
在实际测量中,为了避免后期数据处理中由于坐标转换产生计算误差,在测量前可以建立工件坐标系,此处采用了三二一原理[13]。参见图 4,建立坐标系如下:1)在齿轮轴台上采集3个点,相应地便确定一个基准面x1O1y1,此时该基面的法线方向也确定下来,以该法线方向作为z(z1)轴方向;2)在轴孔表面采集4个点生成一个圆,这时三坐标测量机系统软件自动确定圆心OH,该点将其投影到上一步中生成的平面作为坐标系原点O1;3)在齿轮长轴上采集一点M,按照第二步的方法投影到第一步生成的基准面上,连接投影点MO,连接O1MO,作为第二轴,此时第三轴可通过右手法则自动生成。这样确定下来的工件坐标系只在z方向上与理论坐标系相差一个平移量。
|
图 4 三坐标测量机工件坐标系建立 |
为了确定坐标系的正确性,可以通过轴台上随机测点或检查任意轴孔圆心的方法检验。至此,工件坐标系的全部信息便完全确定。
3 节曲线坐标采集与分析根据上一节的方法,在三坐标测量机上建立好坐标系之后,为了避免侧针与被测齿面或邻侧齿面干涉[14],必须选择合适的测针。选择测针的原则是被测点的切平面与过该点的端平面的交线与测针间的夹角必须大于零,以避免与齿面发生干涉;同时令该夹角尽量小,从而避免测针杆与邻侧齿面干涉。为了便于测量中观察,实验前在齿轮上涂上白色粉末,如图 5所示,完成上述步骤后,便可以开始测量。
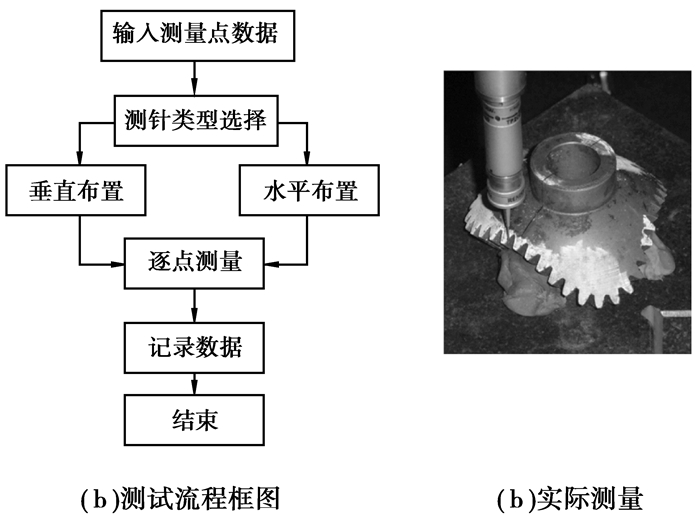
|
图 5 坐标测量 |
通过测量,可以得到同侧齿面节曲线上各点所对应的坐标值,如表 2、表 3所示,分别为三阶椭圆锥齿轮样件对应的测量坐标值和计算坐标值。
| 表 2 三阶椭圆锥齿轮测量坐标值 |
| 表 3 三阶椭圆锥齿轮计算坐标值 |
依据上述的测量数据,即可得到三阶椭圆锥齿轮的测量节曲线,并与理论节曲线对比如图 6所示。
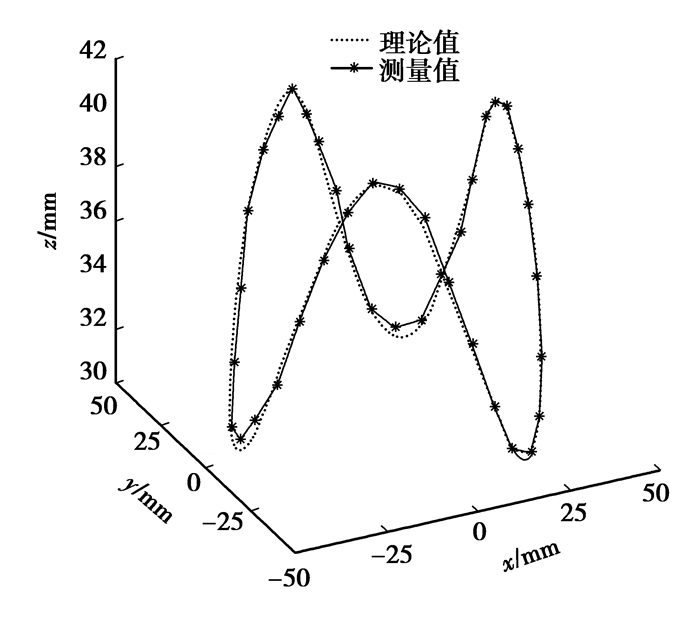
|
图 6 三阶椭圆锥齿轮节曲线测量结果对比 |
由图 6可知,实验得到的节曲线和理论节曲线基本重合,但是高阶椭圆锥齿轮的节曲线是空间球面曲线,要分析节曲线用一般的数学方法很难进行。为了简化实验方案,分别讨论任意两坐标之间的拟合情况。
由式(3)可知
| $ \left\{ \begin{array}{l} x = R\sin \;\delta \cos \;\varphi, \\ y = R\sin \;\delta \sin \;\varphi, \\ z = R\cos \;\varphi 。\end{array} \right. $ | (12) |
得出x,y与自变量
| $ y/x = \tan \varphi, $ | (13) |
x,z与自变量
| $ x/z = \frac{{1 + {e^2} - 2e\cos \;n\varphi }}{{1 - {e^2}}} \cdot \cos \varphi, $ | (14) |
y,z与自变量
| $ y/z = \frac{{1 + {e^2} - 2e\cos \;n\varphi }}{{1 - {e^2}}} \cdot \sin \varphi 。$ | (15) |
由式(13)~式(15)可知,x,y和z的两两之间比值只受
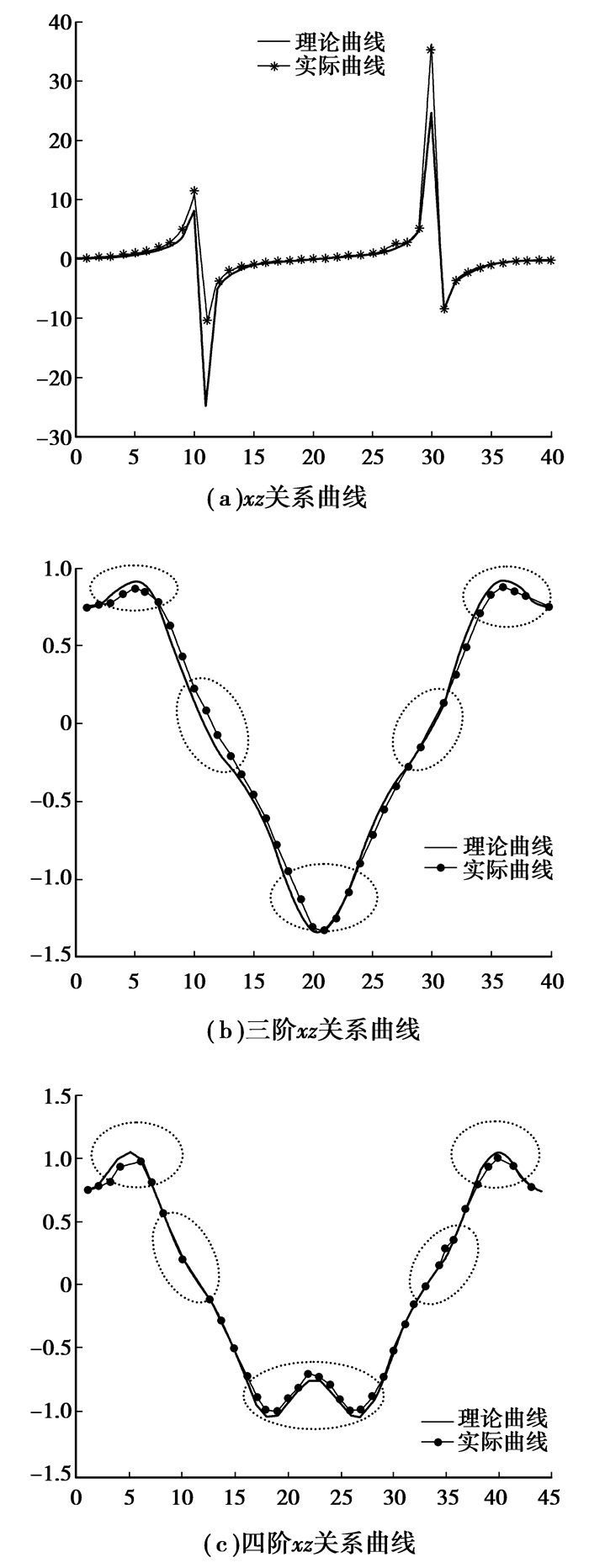
|
图 7 比值曲线 |
根据上图分析可知,实际曲线偏离理论曲线处位于节曲线曲率最小处[3],这是由于在实际加工中,该处加工困难,往往加工出得到的齿形也发生了变化。这对以后椭圆锥齿轮的加工具有指导性意义。
4 高阶椭圆锥齿轮齿距偏差联立式(5)和式(12),可以求得椭圆锥齿轮大端节曲线上同侧齿面的单个齿距,编写Matlab程序。以三阶椭圆锥齿轮为例,根据表 1可知,其单个标准齿距fp3=6.417 801 mm。当齿轮存在齿距偏差时,无论是正值还是负值都会在一对齿啮合完毕而另一对齿进入啮合时,主动齿与被动齿发生冲撞[15]。而单个齿距偏差Δfp3等于实际齿距与理论齿距的代数差为
| $ \Delta {f_{{\rm{p}}i}} = {F_{{\rm{p}}i}} - {f_{{\rm{p}}i}}, $ | (16) |
式中:i为椭圆锥齿轮阶数;Fpi为椭圆锥齿轮的实际齿据。
如图 8所示为单个齿距偏差的柱状图,由图可以看出,单个齿距偏差在零线上下波动,且Δfp3≤±0.8 mm。由于啮合碰撞的存在,单个齿距误差可以直接反映到传动比的波动。
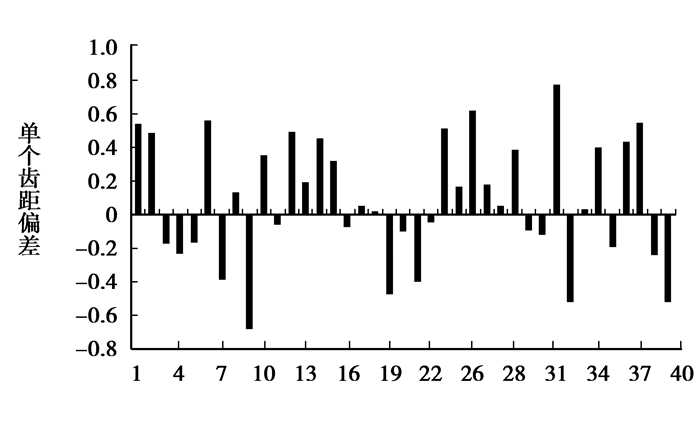
|
图 8 单个齿距偏差柱状图 |
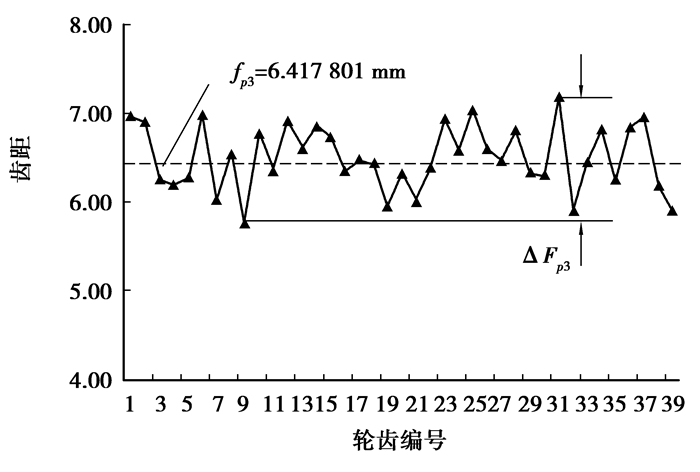
根据单个齿距偏差可以分析计算得到齿轮的最大齿距累计偏差,如图 9所示。
|
图 9 齿距累计偏差曲线 |
由图 9分析可知,椭圆锥齿轮单个齿距曲线在其标准齿距直线附近上下波动,可以计算得到最大齿距累计总偏差ΔFp3=1.438 289 mm,它表现为单个齿距偏差曲线的总幅值,反映了齿轮转一转过程中传动比的变化,因此它影响齿轮传递运动的准确性。由测试计算结果可以看出,通过五轴精铣法加工得到的椭圆锥齿轮具有比较高的运动传递精度。
参考三阶椭圆锥齿轮单个齿距偏差和齿距累计偏差的计算和分析方法,如表 4所示,可以计算分析得到二阶和四阶相应的齿距偏差。
| 表 4 高阶椭圆锥齿轮齿距偏差 |
由于加工得到的齿轮实体参数不尽相同,为了便于对比,通过齿距累计偏差与标准齿距之间的比值ΔFp3/fpi,可以分析得到以下结论:高阶椭圆锥齿轮阶数越高,齿数越多,齿距偏差得越厉害。参考节曲线分析结果可知,阶数越高,齿数越多,节曲线出现内凹现象,加工得到的轮齿变形得越厉害。
5 结论1) 建立了高阶椭圆锥齿轮的节曲线坐标测量模型,给出了椭圆锥齿轮在三坐标测量机上坐标系的建立方式,并推导得到了各个坐标系之间的转换关系。
2) 在三坐标测量机上测量得到了高阶椭圆锥齿轮样件节曲线的坐标点集,进行了有效数据的提取及数据处理。通过分析对比,获得了节曲线偏差的主要原因。由数值分析方法,计算得到了椭圆锥齿轮单个齿距偏差和齿距累计偏差,此方法可以推广到各高阶椭圆锥齿轮。
3) 通过实验及分析,得到了高阶椭圆锥齿轮误差评定的方法,测量分析结果与理论计算结果基本吻合。表明所建立的高阶椭圆锥齿轮齿距误差评定方法是可行的,为非圆锥齿轮的进一步深入研究及推广提供了可靠的依据。
| [1] | XIA Jiqiang, LIU Yuanyuan, GENG Chunming, et al. Noncircular bevel gear transmission with intersecting axes[J]. Journal of Mechanical Design, 2008, 130(5): 1–6. |
| [2] |
林超, 侯玉杰, 龚海, 等.
高阶变性椭圆锥齿轮传动模式设计与分析[J]. 机械工程学报, 2011, 47(13): 131–139.
LIN Chao, HOU Yujie, GONG Hai, et al. Design and analysis of transmission mode for high-order deformed elliptic bevel gears[J]. Journal of Mechanical Engineering, 2011, 47(13): 131–139. (in Chinese) |
| [3] |
赵玉民, 倪俊义, 马延会.
非圆锥齿轮的三维计算机辅助设计[J]. 机械传动, 2010, 34(9): 47–49.
ZHAO Yumin, NI Junyi, MA Yanhui. The 3D modeling of noncircular bevel gear[J]. Journal of Mechanical Transmission, 2010, 34(9): 47–49. (in Chinese) |
| [4] | LIN Chao, HOU Yujie, ZENG Qinglong, et al. The design and experiment of oval bevel geat[J]. Applied Mechanics and Materials, 2011, 86: 297–300. DOI:10.4028/www.scientific.net/AMM.86 |
| [5] |
徐劲力, 黄然.
齿轮齿距偏差和齿距累积误差测量的智能改造[J]. 武汉理工大学学报:信息与管理工程版, 2004, 26(2): 78–79.
XU Julin, HUANG Ran. An Effective way for state-owned enterprise reform by reconstructing traditional enterprise with high-tech industry[J]. Journal of Wuhan University of Technology:Information & Management Engineering, 2004, 26(2): 78–79. (in Chinese) |
| [6] |
许菊若, 沈爱红.
齿轮齿距累积误差的评定[J]. 江南大学学报:自然科学版, 2003, 2(3): 289–292.
XU Juruo, SHEN Aihong. Evaluation of total cumulative pitch error of gear[J]. Journal of Southern Yangtze University:Natural Science Edition, 2003, 2(3): 289–292. (in Chinese) |
| [7] |
颜祯, 黄天喜.
大型螺旋锥齿轮的齿距测量[J]. 机械设计与制造, 2008(11): 208–209.
YAN Zhen, HUANG Tianxi. The pitch measurement of large spiral bevel gear[J]. Machinery Design & Manufacture, 2008(11): 208–209. DOI:10.3969/j.issn.1001-3997.2008.11.083 (in Chinese) |
| [8] | 吴序堂, 王贵海. 非圆齿轮及非匀速比传动[M]. 北京: 机械工业出版社, 1997. |
| [9] |
赵玉民, 马延会, 华林, 等.
非圆锥齿轮节曲线的平面展开算法研究[J]. 中国机械工程, 2008, 19(17): 2046–2049.
ZHAO Yumin, MA Yanhui, HUA Lin, et al. Planar unfolding algorithm of noncircular bevel gears[J]. China Mechanical Engineering, 2008, 19(17): 2046–2049. DOI:10.3321/j.issn:1004-132X.2008.17.007 (in Chinese) |
| [10] | 夏继强, 耿春明, 宋江滨, 等.变传动比相交轴直齿锥齿轮副几何设计方法:中国, 200410009582[P].2004-03-29. |
| [11] | 王开荣, 杨大地. 应用数值分析[M]. 北京: 高等教育出版社, 2010. |
| [12] | 李特文. 齿轮几何学与应用理论[M]. 国楷, 叶凌云, 范琳, 译. 上海: 上海科学技术出版社, 2008. |
| [13] |
王亚平, 王鹏.
三维测量软件系统中坐标系的建立方法[J]. 工业计量, 2004, 14(6): 27–30.
WANG Yaping, WANG Peng. Creation method of coordinate system in 3-D measuring software system[J]. Industrial Measurement, 2004, 14(6): 27–30. (in Chinese) |
| [14] |
王军, 王小椿, 姜虹, 等.
螺旋锥齿轮齿面的三坐标测量[J]. 机械工程学报, 2003, 39(6): 151–154.
WANG Jun, WANG Xiaochun, JIANG Hong, et al. Coordinate measurement of tooth surface of spiral bevel gear[J]. Chinese Journal of Mechanical Engineering, 2003, 39(6): 151–154. (in Chinese) |
| [15] | 张帆, 宋绪丁, 曹源文. 机械精度设计与检测[M]. 西安: 陕西科学技术出版社, 2006. |
 2013, Vol. 36
2013, Vol. 36


